단조 우도비
Monotone likelihood ratio통계에서 단조 우도비 속성은 두 확률 밀도 함수(PDF)의 비율 속성입니다.공식적으로는 분포 θ(x)와 g(x)는 다음과 같은 특성을 가진다.
, 인수x {\ x에서 비율이 감소하지 않는 경우입니다.
함수가 최초 미분 가능한 경우 특성이 다음과 같이 명시될 수 있다.
일부 인수 x에 대한 정의를 충족하는2개의 분포에 대해서는 "x에 MLRP가 있다"고 합니다.일부 통계 T(X)에 관한 정의를 모두 충족하는 분포군의 경우, "T(X)에 MLR이 있다"고 한다.
직감
MLRP는 관측된 변수의 크기와 변수가 도출한 분포 사이에 직접적인 관계를 갖는 데이터 생성 프로세스를 나타내기 위해 사용됩니다.f { f가) {x에 대해 MLRP를 만족하는 x(\x)가 클수록g(\g가 분포 f(\f)에서 도출되었을 가능성이 높아집니다.단조로운 관계에서는 일반적으로 우도 비율입니다.단조성은 통계량에서 특히 최대우도 추정을 사용할 때 유용합니다.또한 MLR을 가진 분포군은 1차 확률 우위 및 위험 비율 증가와 같은 많은 행동 확률적 특성을 가지고 있다.불행하게도, 또한 통상적으로 그렇듯이, 이 가정의 강점은 현실주의의 대가를 치르게 된다.세계의 많은 공정은 입력과 출력 사이에 단조로운 대응관계를 나타내지 않습니다.
예:열심히 일하거나 게으름을 피우다
프로젝트를 진행하고 있으며, 열심히 일하거나 게으름을 피울 수 있다고 가정합니다.선택한 및 의 에 대해 설명합니다가 에 따라 q분배를 유지한다면 작업 이 높을수록 더 열심히 작업한 것 같습니다반대로 품질이 낮을수록 게으름을 피울 가능성이 높아집니다.
- e { , { e \ \ { H , \ } (H는 높음, L은 낮음)를 선택합니다.
- f( e ) { ( q \ e {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ by {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ by by by
- f( e f e가 MLRP를 충족한다고 합니다.재배열하면 종업원이 열심히 일한 확률은
- 이 값은 MLRP에 의해q\로 단조롭게 증가하고 있습니다( )/ ( H { H \ q}) 따라서 어떤 고용주가 "성과 검토"를 하고 있다면 그는 그의 일의 장점으로부터 그의 종업원의 행동을 추론할 수 있다.
MLR을 만족하는 유통 패밀리
통계 모형은 종종 데이터가 일부 분포 계열의 분포에 의해 생성된다고 가정하고 해당 분포를 결정하려고 합니다.패밀리가 모노톤우도비 속성(MLRP)을 가지는 경우, 이 작업은 간소화됩니다.
에 의해 색인화된 밀도함수 { \의 집합 {\displaystyle \theta는 단조비(\})와 같다.f는 임의의 1 < 2 \ _ {1 < \_ {2}、
- 2 ( , 2, x, ) 1 ( 1, 2, x )( \ { f{ \ _ { ) ( X=_ {} , x _ { } , { 3 , \ dots ) { _ f _ { \ { 1 } )
다음으로 유통 제품군은 "MLR (X) \ T ( ) 。
가족 목록
| 가족 | ) { ( ) 。서 f }(는 MLR을 가집니다. |
|---|---|
| {[\ } | \ \i} 관측치 |
| 이항[ { | \ \i} 관측치 |
| 포아송 {[\]} | \ \i} 관측치 |
| 통상 [ \ , \ } | \ \ x} |
가설 검정
랜덤 변수 패밀리의 MLRP가 TX인 경우 : 0 : 0 : 0 0 :\ :> :\ H1 : 0 :\styleq :\display H1 :\ 0 : 0 : the 0 : the most the the the the the the0 : the the the}}0 : the}}0 : the0 : 。
예: 노력과 출력
:\e를 확률적 기술(예: 작업자의 노력)의 입력으로 하고 그 출력은 확률 밀도 fe로 기술합니다f() .\ f(y; e) .다음과 같이}그런 다음 가족은 f{\displaystyle f}의 단조로운 공산비 재산(MLRP):모든 e1e2{\displaystyle e_{1},e_{2}}, e2>e1{\displaystyle e_{2}>, e_{1}}이 f(y;e2)/f의 비율(y;e1){\displaystyle f(의미를 내포하고 표현된다.y;e_{2(y1}} 가 y {y로 증가하고 있습니다
기타 통계 속성과의 관계
단조 우도는 확률 모형뿐만 아니라 점 추정 및 가설 검정과 같은 통계 이론의 여러 영역에서 사용됩니다.
지수 패밀리
단일 모수 지수 군에는 단조 우도 함수가 있습니다.특히, 확률밀도함수 또는 확률질량함수의 1차원 지수 계열은 다음과 같다.
는 충분한 통계 정보 T()에서 단조 비감소 우도비를 가지며, 단, ( ) \ ( \)}가 감쇠하지 않는 경우입니다.
가장 강력한 테스트:칼린-루빈 정리
칼린-루빈 [1]정리에 따르면 단조 우도 함수는 균일하게 가장 강력한 테스트를 구성하기 위해 사용된다.스칼라 파라미터로 파라미터화된 확률밀도함수를 갖는 스칼라측정을 고려하여( ) 1 () / 0 () { =1}(x) / f_{\theta ( \ x x 임의의 에 대해 100 { _ {} \ _ { } (x{ x}가 클수록 { 의 이 높아짐) 임계값 테스트:
- 서 x 0은 E 0 ) {\ \_{\ (X)=\alpha 가 됩니다.
는 사이즈α의 UMP 테스트로 H0 : 대
0: = 0vs의 에서도 정확히 동일한 테스트가 UMP라는 점에 유의하십시오.
중위수 비편향 추정
단조 우도 함수는 요한 판자글 및 [2][3]기타에 의해 지정된 방법을 사용하여 중위수 비편향 추정기를 구성하는 데 사용된다.그러한 절차 중 하나는 평균 비편향 추정기에 대한 Rao-Blackwell 절차의 유사점이다.이 절차는 평균 비편향 추정에 대한 Rao-Blackwell 절차보다 더 작은 등급의 확률 분포에 대해 [3]: 713 유지되지만 손실 함수의 더 큰 등급에 대해 유지됩니다.
수명 분석:서바이벌 분석 및 신뢰성
패밀리 (x ) \ f_{\}(가 T( ) \ T에 우도비 속성을 가지고 있는 경우,
- 의 위험률 감소 단조율은 § 단, 반드시 T {\ T는 아님)이다.
- 패밀리는 x{\ x에서 1차(따라서 2차) 확률적 우위를 보이며, {\displaystyle 의 최적의 베이지안 업데이트는 T {\ T에서 증가하고 있습니다.
단, 단조 위험률이나 확률적 우위는 MLRP를 의미하지 않는다.
증명서
f { \ style _ { \ } 1> 0 \ display \ { 1} > 0> 0 >{ x let let let let let let let let let let let x let let let let let 、 MLR을 만족시킵니다.
또는 동등하게:
이 식을 두 번 통합하면 다음과 같은 결과를 얻을 수 있습니다.
| 1. x에 x0에 {{ 얻기 위해 통합하고 재배치하는 | 2. x부터 부터 x 얻기 위해 통합하고 재배치하는 |
1차 확률 우위
위의 두 부등식을 결합하여 1차 우위를 확보하십시오.
모노톤 위험률
단조로운 위험률을 얻으려면 위의 두 번째 부등식만 사용하십시오.
사용하다
경제학
MLR은 메커니즘 [citation needed]설계에서 에이전트 유형 분포에 대한 중요한 조건입니다.메커니즘 설계 모델에 대한 대부분의 솔루션은 공통 솔루션 [citation needed]방법을 활용하기 위해 MLR을 충족하는 유형 분포를 가정합니다.
레퍼런스
- ^ Casella, G.; Berger, R.L. (2008), 통계 추론, Brooks/Cole. ISBN0-495-39187-5(Theorem 8.3.17)
- ^ Pfanzagl, Johann (1979). "On optimal median unbiased estimators in the presence of nuisance parameters". Annals of Statistics. 7 (1): 187–193. doi:10.1214/aos/1176344563.
- ^ a b Brown, L. D.; Cohen, Arthur; Strawderman, W. E. (1976). "A Complete Class Theorem for Strict Monotone Likelihood Ratio With Applications". Ann. Statist. 4 (4): 712–722. doi:10.1214/aos/1176343543.

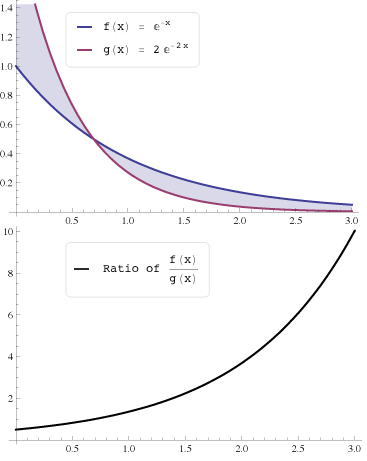

 (는) 단조우도비 속성을 충족합니다.
(는) 단조우도비 속성을 충족합니다. 





 MLRP
MLRP

![{\displaystyle \Pr[e=H\mid q]={\frac {f(q\mid H)}{f(q\mid H)+f(q\mid L)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/458d4ae89a1a59f2f5902b516e9165cfbba77d2e)


 집합 {\displaystyle \theta
집합 {\displaystyle \theta
 단조비(\
단조비(\

 MLR을 가집니다.
MLR을 가집니다.










 E
E







 }}
}}![{\displaystyle {\begin{aligned}&\int _{\min _{x}\in X}^{x_{1}}f_{\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\,dx_{0}\\[6pt]\geq {}&\int _{\min _{x}\in X}^{x_{1}}f_{\theta _{1}}(x_{0})f_{\theta _{0}}(x_{1})\,dx_{0}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/373b58a962111f1b0bf064e01fef654edcd93a8d)

![{\displaystyle {\begin{aligned}&\int _{x_{0}}^{\max _{x}\in X}f_{\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\,dx_{1}\\[6pt]\geq {}&\int _{x_{0}}^{\max _{x}\in X}f_{\theta _{1}}(x_{0})f_{\theta _{0}}(x_{1})\,dx_{1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69fa744ce3f630046b72b0d77f34c5b978b9bc61)






