사면체

정사면체
(회전 모델을 보려면 여기를 클릭)
유형	플라톤 고체
쇼트 코드	3 > 2z
요소들	F = 4, E = 6 V = 4 (표준 = 2)
측면 나란히	4{3}
콘웨이 표기법	T
슐레플리 기호	{3,3}
	h{4,3}, s{2,4}, sr{2,2}
얼굴 구성	V3.3.3
위토프 기호	3 2 3 2 2 2
콕서터 다이어그램	=
대칭	Td, A3, [3,3], (*332)
로테이션 그룹	T, [3,3]+, (332)
레퍼런스	U01, C15, W1
특성.	정다면체
이면각	70.528779° = 아크코스(1×3)
3.3.3 (버텍스 그림)	셀프듀얼 (입체 다면체)
그물

기하학에서, 삼각 피라미드라고도 알려진 사면체(복면체 또는 사면체)는 네 개의 삼각형 면, 여섯 개의 직선 모서리, 그리고 네 개의 꼭지점 모서리로 구성된 다면체이다.사면체는 모든 일반적인 볼록 다면체 중 가장 단순하고 면이 ^[1]5개 미만인 유일한 다면체이다.

사면체는 유클리드 심플렉스의 보다 일반적인 개념의 3차원 케이스이며, 따라서 3차원 심플렉스라고도 불립니다.

사면체는 피라미드의 한 종류로, 평탄한 다각형 밑면과 밑면과 공통점을 연결하는 삼각형 면을 가진 다면체이다.사면체의 경우, 밑면은 삼각형이다(네 개의 면 중 어느 것이든 밑면으로 간주될 수 있다). 그래서 사면체는 "삼각형 피라미드"라고도 한다.

모든 볼록 다면체와 마찬가지로, 사면체는 종이 한 장에서 접을 수 있다.그것은 두 개의 ^[1]그물을 가지고 있다.

모든 사면체에는 4개의 꼭지점이 모두 있는 구(원주구라고 함)와 사면체의 ^[2]면에 접하는 또 다른 구(영감구)가 존재합니다.

정사면체

정4면체는 네 개의 면 모두가 정삼각형인 정4면체이다.이것은 고대부터 알려진 다섯 개의 정칙 플라톤 고체 중 하나입니다.

정4면체에서는 모든 면의 크기와 모양이 동일하고 모서리의 길이가 동일합니다.

정사면체만으로는 테셀레이트(공간 채우기)를 하지 않지만, 정팔면체와 2개의 정사면체와 1개의 팔면체의 비율로 교대로 하면, 그들은 테셀레이션인 교대 입방체 벌집을 형성한다.Schléfli 오르토셈과 힐 사면체를 포함하여 정칙적이지 않은 일부 사면체는 테셀레이트할 수 있습니다.

정4면체는 자기쌍대인데, 이것은 그 쌍대체가 또 다른 정4면체라는 것을 의미한다.이러한 두 개의 이중 사면체로 이루어진 복합 도형은 스텔라 8면체 또는 스텔라 8면체를 형성합니다.

정사면체의 좌표

다음 데카르트 좌표는 원점을 중심으로 모서리 길이가 2인 정사면체와 두 개의 레벨 모서리를 가진 4개의 정점을 정의합니다.

$\displaystyle \left(\pm 1,0,-{\frac {1}{\frac rt {2}}\오른쪽)\displays \mbox {and}\left(0,\pm 1, {1}{\frac rt {2}}\right}\displaystyle$

단위 구면에서 대칭적으로 4개의 점, 원점에서 중심, 낮은 면 수준에서 표현되는 정점은 다음과 같습니다.

$({displaystyle v_1}=\leftrt {frac {8}{9}}},0,-{\frac {1}{3}}}\right)}$

$(\displaystyle v_{2}=\leftrt {\frac {2} {9}}, {\frac {2} {3}},-{\frac {1}{3}}},\right})$

$\displaystyle v_{3}=\leftrt {\frac {2} {9}},-{\fracrt {2} {3}},-{\frac {1}{3}},\right}$

${\displaystyle v_{4}=(0,0,1)}$

엣지 길이는 8.$($ 스타일 ${8}{3$입니다.

또 다른 좌표 세트는 모서리 길이가 2인 교대 입방체 또는 데미큐브를 기반으로 한다.이 양식에는 Coxeter 다이어그램과 Schléfli 기호 h{4,3}가 있습니다.이 경우 사면체의 모서리 길이는 2⁄2이다.이러한 좌표를 반전시키면 이중 사면체가 생성되고, 쌍은 함께 스텔레이트된 8면체를 형성하며, 정점은 원래 입방체의 정점이다.

사면체: (1,1,1), (1,-1,-1), (-1,-1), (-1,-1), (-1,-1,-1)

이중 사면체: (-1,-1,-1), (-1,-1), (1,-1), (1,-1,-1)

각도 및 거리

모서리 길이가 a인 정4면체의 경우:

얼굴 영역	$({displaystyle A_{0}=blac {4}}:a^{2},}$
표면적[3]	${\displaystyle A=4,A_{0}=sqrt {3}}:a^{2},}$
피라미드 높이[4]	${\displaystyle h=marcfrac {6}{3}}a=marcrt {2}{3}},a,}$
중심에서 정점까지의 거리	$({displaystyle {frac {3}{4},h=param frac {6}{4},a=paramrt {3}{8}},a,a})$
모서리에서 반대쪽 모서리까지의 거리	${\displaystyle l=black {1}{\displayrt {2}},a,}$
용량[3]	${\displaystyle V=black {1}{3}}A_{0}h=beakfrac {{12}}a^{3}=beakfrac {a^{3}}{6beakrt {2}},$
면-버텍스 엣지 각도	$(\displaystyle \arccos \left\frac {1}{\arctan {3}\right)=\arctan \leftrt {2}}\right),$ (약 54.7356°)
면 모서리-면 각도, 즉 "이면각"[3]	${\displaystyle \arccos \left\frac {1}{3}}\right}=\arctan \left(2440rt {2}}\right),$ (약 70.5288°)
정점-중심-버텍스 각도,[5] 사면체 중심에서 두 정점까지의 선 사이의 각도입니다.정점에서 고원 경계 사이의 각도이기도 합니다.화학에서는 이것을 사면체 결합각이라고 부른다.이 각도(라디안 단위)는 또한 사면체의 한쪽 모서리를 구에 중앙으로 투영한 결과 단위 구상의 원형 호 길이입니다.	$(\displaystyle \arccos \leftfrac {1}{3}}\right)=2\arctan \leftfrt {2}\right),$ (약 109.4712°)
면에 의해 하위 조정된 정점의 입체 각도	$(\displaystyle\arccos\leftfrac{23}{27}\right)}$ (약 0.55129 스테라디안) (약 1809.8 평방도)
원주[3] 반지름	${\displaystyle R=param frac {6} {4}}a=paramrt {3} {8}},a,}$
면에[3] 접하는 영감의 반지름	${\displaystyle r=syslogfrac {1}{3}}R=syslogfrac {a}{\syslogrt {24}},$
모서리에[3] 접하는 중심구의 반지름	${\displaystyle r_{\mathrm {M}}=syslogrt {rR}}=syslogfrac {a}{\syslogrt {8}},}$
외기반경	${\displaystyle r_{\mathrm {E}}=syslogfrac {a}{\syslogrt {6}},$
반대쪽 정점에서 엑스피어 중심까지의 거리	${\displaystyle d_{\mathrm {VE} = frac {6} {2} a = frac {3} {2} a ,$

베이스평면에 대하여 면의 기울기(222)는 에지의 2배이며, 에지를 따라 베이스에서 꼭대기까지의 수평거리가 면의 중앙을 따라 있는 수평거리(222)의 2배에 해당한다.즉, C가 베이스의 중심이라면 C에서 베이스의 정점까지의 거리는 C에서 베이스의 가장자리 중간점까지의 거리의 2배가 된다.이는 삼각형의 중위수가 중심에서 교차하고 이 점이 각 세그먼트를 두 개의 세그먼트로 나누고, 두 세그먼트 중 하나는 다른 세그먼트보다 두 배 더 깁니다(증거 참조).

변 길이 a, 그 외접 구체의 반지름 R, 그리고 3공간에서 임의의 점으로부터 그것의 4개의 꼭지점까지의 거리_i d를 가진 정4면체의 경우, 우리는 다음을^[6] 가진다.

${\displaystyle {\frac {d_{1}^{2}^{4}+d_{3}^{4}+d_{4}{4}+{4}}+{\frac {16R^{4}}{9}}&\left({\frac {d_{1}^{2}+d_{2})}^{2}+d_{3}^{2}+d_{4}^{2}}{4}+{\frac {2R^{2}{3}}\right}^{2};\4\left(a^4}+d_{1}^4}+d_{3}^4}+d_{4}+d_{3}^4}+d_{4}+d_{4}+left(a^2}\right)&\frac{2}{1}^{2}{2}{1}{1}{1}{1}}}}}}}}}}}}}{{{{{}}}}}}}}}}}}}}}}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\right)^{2}.\end { aligned}}$

정사면체의 등각성

정육면체의 정점은 각각 정사면체를 형성하는 4개씩의 두 그룹으로 그룹화할 수 있습니다(위 및 애니메이션 참조, 정육면체의 두 사면체 중 하나를 보여줍니다).정사면체의 대칭은 큐브의 대칭의 절반에 해당합니다. 즉, 정사면체를 서로 매핑하지 않고 자신에게 매핑하는 대칭입니다.

사면체는 점 반전에 의해 자신에게 매핑되지 않은 유일한 플라톤 고체입니다.

정4면체는 대칭군_d T, [3,3], (*332), 대칭군 S와₄ 동형인 24개의 등각체를 가진다.다음과 같이 분류할 수 있습니다.

• T, [3,3],⁺ (332)는 다음과 같은 켤레 등급의 교대군₄ A(항등성과 11개의 적절한 회전)와 동형이다(괄호 안에 정점 또는 그에 상응하는 면의 순열과 단위 사분위 표현).
  • 아이덴티티(표준; 1)
  • 반대 평면에 수직인 정점을 통해 ±120°의 각도로 축을 회전시킵니다.4축, 1축당 2개, 함께 8개((1 2 3개) 등) 1 ± i ± j ± k/2)
  • 가장자리가 반대쪽 가장자리로 매핑되도록 180° 회전: 3(1)(2)(34) 등; i, j, k)
• 모서리에 수직인 평면에서의 반사: 6
• 평면에 수직인 축에 대한 90° 회전과 결합된 평면에서의 반사: 3축, 축당 2개, 함께 6개. 동등하게, 그것들은 반전(x는 -x에 매핑됨)과 결합된 90° 회전이다: 면축에 대한 입방체의 회전과 일치한다.

정사면체의 직교 투영

정4면체에는 두 개의 특별한 직교 투영법이 있습니다. 하나는 정점 중심 또는 동일 면에 있고 다른 하나는 모서리에 있습니다.첫₂ 번째는 A Coxeter 평면에 해당합니다.

맞춤법 투영법

중심	면/버텍스	엣지
이미지
투사적 대칭	[3]	[4]

정사면체의 단면

정사면체의 수직 반대쪽 모서리 두 개가 평행 평면 집합을 정의합니다.이러한 평면 중 하나가 사면체와 교차할 때 결과적으로 발생하는 단면은 ^[7]직사각형입니다.교차 평면이 모서리 중 하나 근처에 있으면 직사각형이 길고 가늘습니다.두 모서리 사이의 중간 지점에 교차로가 정사각형입니다.이 중간점을 지날 때 사각형의 가로 세로 비율이 반전됩니다.중간점 정사각형 교차점의 경우 결과 경계선이 사면체의 모든 면을 비슷하게 횡단합니다.만약 사면체가 이 평면에서 이등분된다면, 양쪽의 반쪽은 웨지가 된다.

이 속성은 두 개의 특수 에지 쌍에 적용될 때 사각형 디셰노이드에도 적용됩니다.

구면 타일링

사면체는 구면 타일링으로 표현될 수도 있고 입체 투영을 통해 평면 위에 투영될 수도 있습니다.이 투영법은 적합하며 각도는 보존되지만 면적이나 길이는 보존되지 않습니다.구면의 직선은 평면에 원형 호로 투영됩니다.

맞춤법 투영법	입체 투영

헬리컬 스태킹

정사면체는 Boerdijk-Coxeter 나선이라고 불리는 키랄 비주기 사슬에 마주보고 쌓일 수 있다.

4차원에서는 4면체 셀(5셀, 16셀 및 600셀)을 가진 모든 볼록한 정4폴리톱은 이들 사슬에 의해 3구체의 타일링으로 구성될 수 있으며, 이들 사슬은 4폴리톱 경계면의 3차원 공간에서 주기적으로 된다.

불규칙 사면체

사면체 대칭 부분군 관계

사면체도에 나타난 사면체 대칭

4개의 정삼각형 면을 가지지 않는 사각형은 그들이 가진 대칭에 따라 분류되고 이름이 붙여진다.

만약 정사면체의 반대쪽 모서리의 세 쌍이 모두 수직이라면, 그것은 직각 사면체라고 불립니다.한 쌍의 반대쪽 모서리만 수직일 때, 그것은 반정밀 사면체라고 불립니다.

등역학적 사면체는 정점을 반대 면의 인자에 결합하는 세비안이 동시에 존재하는 면이다.

등각 사면체는 정점을 사면체의 내접구와의 반대면 접점에 결합하는 동시 세비안을 가진다.

삼각사면체

3각형의 사면체에서 한 정점의 세 면각은 입방체의 모서리와 같이 직각이다.

케플러는 정육면체, 정사면체,^[8] 정사면체 사이의 관계를 발견했다.

디스헤이드

디셰노이드라고도 불리는 이등변 사면체는 네 개의 면 모두가 합동 예각 삼각형이고 서로 마주보는 두 모서리의 길이가 같은 사면체이다.정4면체는 디페노이드의 특별한 경우이다.

오르소셈

3정격은 네 개의 면이 모두 직각 ^[a]삼각형인 사면체이다.오르토셈은 모든 가장자리가 서로 수직인 나무의 볼록한 껍질인 불규칙한 단순체입니다.3차원 오르소셈에서 트리는 두 개의 직각 회전을 하는 선형 경로에서 네 개의 정점을 모두 연결하는 세 개의 수직 가장자리로 구성됩니다.3정격은 두 꼭지점 각각에 두 개의 직각을 가진 사면체이기 때문에 다른 이름은 쌍각사면체이다.그것은 4개의 ^[9]직각을 가지고 있기 때문에 사각형 사면체라고도 불린다.

콕서터는 또한 정다각형과 대칭 그룹에 ^[10]대한 그들의 일체적 관계 때문에 사각형 사면체 특성 사면체라고 부른다.예를 들어, 길이가 같은 수직 모서리를 가진 3정통체의 특수한 경우는 입방체의 특성이며, 이는 입방체가 이 정통의 인스턴스로 세분될 수 있음을 의미합니다.세 개의 수직 가장자리가 단위 길이일 경우 나머지 가장자리는 길이 θ2와 길이 θ3 중 하나이므로 모든 가장자리는 입방체의 가장자리 또는 대각선이다.큐브는 6개의 다른 방법으로 3개의 정육면체를 해부할 수 있으며, 6개 모두 대각선 33개의 정육면체를 둘러싸고 있다.입방체는 또한 동일한 특징의 3정칙의 48개의 작은 인스턴스(한 ^[b]번에 대칭 평면에 의해 한 방향으로만)로 해부할 수 있습니다.입방체의 특징적인 사면체는 헤론식 사면체의 한 예이다.

정4면체를 포함한 모든 정다각형은 특유의 오르토셈을 ^[c]가지고 있다.정4면체의 특징적인 사면체인 3정통체도 있다.정사면체는 ^[d]대칭면에 의해 특징적인 사면체의 24가지 사례로 세분된다.

사면체의 모서리 길이가 2인 경우, 특징적인 사면체의 모서리 $길이$는 $({$$${$1$ 1$({displaystyle$ 1$\}),$ $({$ + ${\displaystyle \sqrt{\frac{3}{}}}$(외부 오른쪽 면, 사면체의 특징적인 삼각형)이다.$({displaystyle {tfrac {$3$}$ ${2$ 1, $($ ${\displaystyle \sqrt{\frac{1}{}}}$, 6$($^[13]$displaystyle {tfrac {1}{6}})$입니다.직교 가장자리를 따르는 3자 경로는 $(디스플레이 스타일$ 1$),$ ${\displaystyle \sqrt{\frac{1}{}}}$($디스플레이$ 스타일 1$),$ 3$($디스플레이 스타일$1$ 1(디스플레이 스타일 1), $($ 스타일 $1({$ {$tfrac {1}{6$입니다. 처음에는 사면체 정점에서 사면체 모서리 중앙으로 이동한 다음 90°에서 테면체 중앙으로 회전합니다.사면체 중심오르소셈은 4개의 서로 다른 직각 삼각형 면을 가지고 있습니다.외부 면은 30-60-90 삼각형으로, 사면체 면의 6분의 1입니다.정사면체 내부의 세 면은 $모서리$가$1인$ 직각 $,$ 1인 직각 $삼각형$ $1인$ 직각 $삼각형{\displaystyle \sqrt{\frac{\mathrm{}}{}}}$,$1인$ 직각 $삼각형$$,$ $1인{\displaystyle \sqrt{\frac{\mathrm{}}{}}}$ 직각 $삼각형$, $1인$ 직각 삼각형$,$ ${\displaystyle \sqrt{\frac{\mathrm{1인}}{}}}$ 직각 삼각형, $1인$ 직각 $삼각형$, 1인 직각 $삼각형{\displaystyle \sqrt{\frac{\mathrm{}}{}}}$$,$ 1인 직각 삼각형$,$ 1인 직각 $삼각형$입니다$.$$(*$$displaystyle$ {$tfrac$ {$}$$$${2}}), (*displaystyle$ ${\$ {\$displaystyle$ ${\tfrac$ {1$}{2}}),$ $(*$$displaystyle$ ${\$$displaystyle$ {\$tfrac$ {$1}{6$ $(*$ ${\$displaystyle {\$t$ {\tfrac {4} {\$tfrac$$}$ {\t} {\t} {\tfrac$}$ {\t} ${{{{{{{{{{{{{$

공간 채우기 사면체

공간을 채우는 사면체 팩은 타일 ^[14]공간에 직접 일치하거나 반동형(미러 이미지) 복사로 구성됩니다.입방체를 3개의 정방향과 3개의 오른손(각 입방체 면에 각각 하나씩) 6개의 정방향으로 분할할 수 있으며, 입방체는 공간을 채울 수 있기 때문에 이러한 의미에서 ^[e]정방체의 특징적인 3정방향은 공간을 채우는 4면체이다.디셰노이드는 디셰노이드의 사면체 벌집과 같이 직접 합동적인 의미에서 공간을 채우는 사면체일 수 있다.그러나 일반 사면체만으로는 ^[f]공간을 채울 수 없다.

기본 도메인

대칭군의 기본^[15] 영역인 불규칙 사면체는 구르사트 사면체의 한 예이다.구르사트 사면체는 거울 반사에 의해 모든 규칙적인 다면체(그리고 많은 다른 균일한 다면체)를 생성하는데, 이 과정은 위토프의 만화경 구조라고 불립니다.

다면체의 경우 위토프의 건축은 만화경처럼 거울 3개를 서로 비스듬히 배열합니다.원통형 만화경과는 달리 위토프의 거울은 구르사트 사면체의 세 면에 위치해 있어 세 거울이 모두 한 ^[g]지점에서 교차한다.

3차원 허니콤을 생성하는 구르사트 사면체 중에서 우리는 위에서 ^[10]설명한 것과 같은 오르소셈(입방체의 특징적인 사면체), 이중 오르소셈(입방체의 특징적인 사면체) 및 공간을 채우는 디스포이드를 인식할 수 있다.디셰노이드는 거울 이미지에 결합된 이중 오르토셈(사중 오르토셈)입니다.따라서 이 세 개의 구르사트 사면체와 반사에 의해 생성되는 모든 다면체는 큐브의 특징적인 사면체로 해부할 수 있습니다.

불규칙 사면체의 등각성

불규칙(표시되지 않은) 사면체의 등각은 사면체의 형상에 따라 달라지며, 7가지 경우가 가능합니다.각 경우에 3차원 점군이 형성된다.면 또는 가장자리 표시가 포함된 경우 두 개의 다른 등각선(C₃, [3])⁺ 및 (S₄, [2⁺,4⁺])이 존재할 수 있습니다.사면체 다이어그램은 아래의 각 유형에 대해 포함되며 모서리는 등각 등가로 색칠되며 고유한 모서리를 위해 회색으로 색칠됩니다.

사면체 이름				엣지 등가 도표	묘사
대칭
숀.	콕스.	오브.	오드
정사면체					4개의 정삼각형 그것은 대칭군 S와4 동형인 대칭군d T를 형성한다. 정4면체는 콕서터 다이어그램과 슐레플리 기호 {3,3}을 가진다.
Td T	[3,3] [3,3]+	*332 332	24 12
삼각형 피라미드					정삼각형 밑면과 등각삼각형 변 3개 베이스의 6개의 등각선에 해당하는 6개의 등각선을 제공합니다.정점의 순열로서 이들 6개의 등각선은 항등식 1, (123), (132), (12), (13) 및 (23)이며 대칭군3v C를 형성하고 대칭군 S와3 동형이다.삼각형 피라미드는 슐레플리 기호 {3}δ( )를 가진다.
C3V C3.	[3] [3]+	*33 33	6 3
미러 회전체					공통 기저 모서리를 가진 두 개의 동일한 스칼렌 삼각형 여기에는 동일한 에지(1,3), (1,4), (2,3), (2,4)의 두 쌍이 있으며, 그렇지 않으면 동일한 에지가 없습니다.유일한 두 등각은 1과 반사(34)이며, 그룹s C는 순환 그룹 Z와2 동형이다.
Cs =C1h =C1v	[ ]	*	2
불규칙 사면체 (대칭 없음)					네 개의 부등삼각형 유일한 등각은 항등식이고 대칭군은 사소한 군이다.불규칙 사면체는 슐레플리 기호 ( ) ) ( )( ( )( ( )( ( )을 가진다.
C1.	[ ]+	1	1
디스헤노이드(등각 삼각형 4개)
사각형 디스포이드					4개의 이등변 삼각형 그것은 8개의 등각선을 가지고 있다.엣지(1,2)와 (3,4)의 길이가 다른 경우, 8개의 등각선은 동일 1, 반사(12)와 (34), 180° 회전(12)(34)와 (13)(24)(23)와 부적절한2d 90° 회전(1234)과 (1432)이다.사각형 디셰노이드는 콕서터 다이어그램과 슐레플리 기호 s{2,4}를 가진다.
D2D S4.	[2+,4] [2+,4+]	2*2 2×	8 4
마름모꼴 디스테노이드					4개의 동일한 스칼레네 삼각형 그것은 4개의 등각선을 가지고 있다.등각선은 1과 180° 회전(12)(34)(13)(24)(23)(23)(23)입니다.이것은 점 그룹2 D로 나타나는 클라인의 4개4 그룹 V 또는22 Z입니다.마름모꼴 디셰노이드는 Coxeter 다이어그램과 Schléfli 기호 sr{2,2}를 가진다.
D2	[2,2]+	222	4
일반화 디스포이드(2쌍의 등삼각형)
이원적 디스포이드					같은 이등변 삼각형의 두 쌍 이렇게 하면 수직이지만 길이가 다른 두 개의 반대쪽 가장자리(1,2)와 (3,4)를 얻을 수 있으며, 4개의 등각선은 1, 반사(12)와 (34)와 180° 회전(12)(34)이 됩니다.대칭 그룹은 C이며2v 클라인 4-그룹4 V와 동형입니다.이항 디스포노이드는 슐레플리 기호 {}{{ }을(를) 가집니다.
C2V C2	[2] [2]+	*22 22	4 2
필릭 디스테노이드					두 쌍의 동일한 스칼렌 또는 이등변 삼각형 여기에는 동일한 에지(1,3), (2,4) 및 (1,4), (2,3)의 두 쌍이 있지만, 그렇지 않으면 동일한 에지는 없습니다.유일한 두 등각계는 1과 회전(12)(34)이며, C군은 순환군2 Z와2 동형이다.
C2	[2]+	22	2

일반 속성

용량

사면체의 부피는 피라미드 부피 공식에 의해 주어진다.

${\displaystyle V=black {1}{3}}A_{0},h,}$

여기서₀ A는 베이스의 면적이고 h는 베이스에서 정점까지의 높이입니다.이것은 베이스의 네 가지 선택 각각에 적용되므로 첨단에서 반대 면까지의 거리는 이들 면적의 면적에 반비례합니다.

정점이 a = (a₁, a₂, a₃), b = (b₁, b₂, b₃), c = (c₁, c₂, c₃) 및 d = (d₁, d₂, d₃)인 사면체의 경우, 부피는 1/6 det(a - d, b - d, c - d) 또는 단순하게 연결된 정점 쌍의 다른 조합이다.이것은 점곱과 교차곱을 사용하여 다시 작성할 수 있으며, 다음과 같이 됩니다.

${\displaystyle V=sqffrac {(\mathbf {a} -\mathbf {d})\cdot(\mathbf {b} -\mathbf {d})\times(\mathbf {c} -\mathbf {d}) }}}.}$

좌표계의 원점이 정점 d와 일치하도록 선택되면, d = 0이다.

$(\displaystyle V=syslogfrac {\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ) } {6} )$

여기서 a, b, c는 하나의 정점에서 만나는 세 개의 모서리를 나타내며, a · (b × c)는 스칼라 삼중곱이다.이 공식과 평행입방체의 부피를 계산하는 데 사용된 공식과 비교하여, 우리는 사면체의 부피가 3개의 수렴 모서리를 공유하는 평행입방체의 부피의 1/6과 동일하다고 결론지었다.

스칼라 삼중곱의 절대값은 다음과 같은 결정 인자의 절대값으로 나타낼 수 있다.

6⋅ V=‖ abc‖{\displaystyle 6\cdot V={\begin{Vmatrix}\mathbf{를}&\mathbf{b}&\mathbf{c}\end{Vmatrix}}}또는 6⋅ V=‖ abc‖{\displaystyle 6\cdot V={\begin{Vmatrix}\mathbf{를}\\\mathbf{b}\\\mathbf{c}\end{Vmatrix}}}이{a=(1,2,3. ), ${\displaystyle \begin{array}{l}\mathbf{b}\end{array}}$ ${\displaystyle \begin{array}{l}=\end{array}}$ ( ${\displaystyle \begin{array}{l}{b\mathrm{}}_{}{}_{}\end{array}}$, b${\displaystyle \begin{array}{l}{}_{}{}_{}\end{array}}$, b${\displaystyle \begin{array}{l}{}_{}{3\mathrm{}}_{}\end{array}}$) , ${\displaystyle \begin{array}{}c\\ \mathbf{}\end{array}}$ ${\displaystyle \begin{array}{l}=\end{array}}$ ( ${\displaystyle \begin{array}{l}{c\mathrm{}}_{}\end{array}}$1, ${\displaystyle \begin{array}{l}{c\mathrm{}}_{}\end{array}}$2, ${\displaystyle \begin{array}{l}{c\mathrm{}}_{}\end{array}}$3${\displaystyle \begin{array}{l}\end{array}}$)${\displaystyle \begin{array}{}\end{array}}$, \ $style { case$} \ $mathbf { a$ } = ( $a$_ {$1$ , a$_$ { $2$} , \ \ $mathbf {$ b = ( $b _$1 , $b$_ b _$2$ , b )$_$ { 3 } \ $f$、 \ f$。$

이런 이유로

36⋅ V2-12는 ⋅ b는 ⋅하 ⋅ bb2b⋅하 ⋅ cb⋅ cc2{\displaystyle 36\cdot V^{2}={\begin{vmatrix}\mathbf{a^{2}}&\mathbf{를}\cdot \mathbf{b}&\mathbf{를}\cdot \mathbf{c}\\\mathbf{를}\cdot \mathbf{b}&\mathbf{b^{2}}&\mathbf{b}\cdo.t \mathbf{c}\\\mathbf{를}\cdot \mathbf{c}&\mathbf{b}\cdot \mathbf{c}&\mathbf{c^{2}}\end{vmatrix}}}이{한 ⋅ b)b. 왜냐하면 ⁡ γ, b(c)bc. 왜냐하면 ⁡ α, ⋅의 4c. 왜냐하면 ⁡ β.{\displaystyle{\begin{경우}\mathbf{를}\cdot \mathbf{b}=ab\cos{c}=bc\cos{\alpha},\\ \mathbf{b}\cdot{\gamma},\\\mathbf.\mathbf ${a} \cdot \mathbf {c} = ac\cos {cos }$$。$$\end {case}}$

그러면

${\displaystyle V=vfrac {6}{\cosrt {1+2\cos}\cos {\cos }-\cos ^{2}-\cos ^{2}{\cos },},}$

여기서 α, β, θ는 정점 d에서 발생하는 평면 각도이다.각도α는 정점 d와 정점 b와 c를 연결하는 두 가장자리 사이의 각도입니다.각도 β는 정점 a와 c에 대해 동일하지만 θ는 정점 a와 b의 위치에 의해 정의된다.

d = 0 이 필요하지 않은 경우

${\displaystyle 6\cdot V=\left \det \det {filters}a_{1}&b_{1}&d_{2}&c_{2}&d_{2}\a_{3}&d1}&b_{1}&b_{1}&b_{1}&b_{1}&b_{1}&b_{b_{1}&b_{1}&b_b_{b_{b_{2}&b_{b_{f}&b_{2}&b_{2}&b_{c_{2}\c_{2}&}$

사면체의 꼭지점 사이의 거리를 고려할 때, 부피는 케일리-멘저 행렬식을 사용하여 계산할 수 있다.

${{displaystyle 288\cdot V^{2}=begin{vmatrix}0&1&1&1&1&0&d_{12}^{2}&d_{13}^{2}{1&d_{12}^{2}{2}^{2}&0&d_23}^{d}^{d}^2}^1&1&1&1&1&2}$

여기서 첨자 i, j { {1, 2, 3, 4}는 정점 {a, b, c, d}을 나타내며_ij, d는 두 정점을 연결하는 가장자리 길이이다.행렬식의 음수 값은 주어진 거리로 사면체를 구성할 수 없음을 의미합니다.때때로 타르타글리아의 공식이라고 불리는 이 공식은 본질적으로 15세기 화가 피에로 델라 프란체스카에 기인하며,^[16] 삼각형 면적에 대한 1세기 헤론의 공식의 3차원 유사체이다.

a, b, c는 한 점에서 만나는 세 개의 에지이고 x, y, z는 반대 에지임을 나타냅니다.V를 사면체의 부피라고 하자^[17].

${\displaystyle V=sqrt {4a^{2}b^{2}c^{2}-a^{2}X^{2}-b^{2}Y^{2}-c^{2}Z^{2}+XYZ}} {12}}$

어디에

$\displaystyle {\begin{aligned}X&=b^{2}+c^{2}-x^{2},\Y&=a^{2}+b^{2}-z^{2}.\end { aligned}}$

위의 공식은 모서리 길이 6개를 사용하며, 다음 공식은 모서리 길이 3개와 각도 3개를 사용합니다.

${\displaystyle V=vfrac {6}{\cosrt {1+2\cos}\cos {\cos }-\cos ^{2}-\cos ^{2}{\cos }}}-\cos ^{2}{\cos }}}}$

왜가리형 사면체 체적 공식

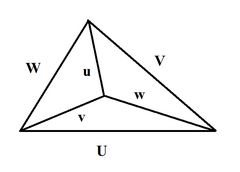
U, V, W, u, v, w가 사면체의 모서리 길이일 경우(처음 세 개는 삼각형을 이루고 u는 U 반대편, v는 V 반대편, w는 W 반대편^[18]),

${\displaystyle V=frac {,(-p+q+r+s),(p-q+r+s),(p+q+r+s),(p+q+r-s)}}{192,u,v,w}}$

어디에

${\displaystyle {narged}p&=sqrt {xYZ},&q&=sqrt {yZX},&r&=sqrt {zX}Y}}, &s&=sqrt {xyz},\end {aligned}}$

${\displaystyle {begin{aligned}X&=(w-U+v),(U+v+w),&x&=(U-v+w),(v-w+U),\\\Y&=(u-V+w), (V+w+u), &y=(V-w+u), (w-u+V), \Z&=(v-W+u), (W+u+v), &z&=(W-u+v), (u+W)\end { aligned}}$

볼륨 분할기

사면체의 바이메디언(대면 모서리의 중간점 연결기)을 포함하는 평면은 ^[19]사면체의 부피를 이등분합니다.

비유클리드 권

쌍곡선 공간이나 3차원 타원 기하학에서 사면체의 경우, 사면체의 이면각은 그 모양과 부피를 결정한다.이 경우, 무라카미로부터 부피가 주어집니다.야노 ^[20]공식하지만, 유클리드 공간에서, 사면체의 축척은 그것의 부피를 변화시키지만 그것의 이면각은 변하지 않기 때문에, 그러한 공식은 존재할 수 없다.

가장자리 사이의 거리

사면체의 반대편 두 모서리는 두 개의 스큐 선 위에 있으며, 모서리 사이의 거리는 두 스큐 선 사이의 거리로 정의됩니다.d는 여기서 계산한 것과 같이 반대쪽 가장자리 a와 b - c에 의해 형성된 스큐 라인 사이의 거리라고 하자.그리고 또 다른 부피 공식은 다음과 같이 주어진다.

${\displaystyle V=syslogfrac {d(\mathbf {a} \times \mathbf {(b-c)}) }{6}}.}$

삼각형과 유사한 특성

사면체는 영감, 원주체, 내측 사면체, 외구체 등 삼각형과 유사한 특성을 많이 가지고 있다.여기에는 인센티브, 원주위 중심, 외부 중심, Spiker 중심 및 중심과 같은 점이 각각 있습니다.그러나 일반적으로 교차하는 ^[21]고도에 대한 직교 중심은 없습니다.

Gaspard Monge는 모든 사면체에 존재하는 중심을 발견했는데, 지금은 Monge 점으로 알려져 있다. 즉, 사면체의 6개의 중간면이 교차하는 지점이다.미드플레인은 다른 두 정점을 결합함으로써 형성된 반대쪽 모서리의 중심도 포함하는 두 정점을 결합하는 모서리에 직교하는 평면으로 정의됩니다.만약 사면체의 고도가 교차한다면, Monge 점과 직교 중심은 직교 중심 사면체의 클래스를 제공하기 위해 일치합니다.

Monge 점에서 임의의 면으로 떨어진 직교 선은 해당 면의 직교 중심과 반대 정점에서 떨어진 고도 피트 사이의 선분 중간 지점에서 해당 면과 만난다.

사면체의 정점과 반대면의 중심을 연결하는 선분을 중앙값이라고 하고, 반대쪽 두 모서리의 중간점을 연결하는 선분을 사면체의 쌍면체라고 한다.그래서 4면체에는 4개의 중간자와 3개의 쌍각자가 있다.이 7개의 선분들은 모두 사면체의 ^[22]중심이라고 불리는 점에서 동시에 나타납니다.또한 네 개의 중위수는 중심별로 3:1 비율로 나뉩니다(코만디노의 정리 참조).사면체의 중심은 몽게점과 원주점 사이의 중간점이다.이 점들은 삼각형의 오일러 선과 유사한 사면체의 오일러 선을 정의합니다.

일반 삼각형의 9점 원은 사면체의 내측 사면체 원주에 유사점이 있다.그것은 12점 구이고 기준 사면체의 네 면의 중심 외에, 그것은 몽게 점에서 네 개의 꼭지점 각각을 향해 1/3인 네 개의 대체 오일러 점을 통과합니다.마지막으로 각 오일러 점에서 떨어진 직교선의 네 개의 기준점을 통과하여 오일러 ^[23]점을 생성한 정점을 포함하지 않는 면으로 이동합니다.

12점 구체의 중심 T는 또한 오일러 선 위에 있다.삼각형의 중심과 달리, 이 중심은 Monge 점 M에서 원주 중심으로 가는 길의 3분의 1에 있습니다.또, T를 통과하는 선택면에 대한 직교선은, 같은 면에 다른 2개의 직교선과 동일면에 대한 코프라어이다.첫 번째는 해당 오일러 점을 지나 선택된 면으로 가는 직교 선입니다.두 번째는 선택한 면의 중심을 통과하는 직교 선입니다.12점 중심을 통과하는 이 직교 선은 오일러 점 직교 선과 중심 직교 선 사이의 중간에 있습니다.또한 모든 면에 대해 12점 중심은 대응하는 오일러 점의 중간점과 해당 면에 대한 직교 중심에 있습니다.

12점 구체의 반지름은 기준 사면체의 원주 반지름의 1/3이다.

에 의해 주어진^[24] 일반 사면체의 면에 의해 만들어진 각들 사이에 관계가 있다.

${\displaystyle{\begin{vmatrix}-1&, \cos{(\alpha_{12})}&, \cos{(\alpha_{13})}&,\cos{(\alpha_{14})}\\\cos{(\alpha_{12})}&, -1&, \cos{(\alpha_{23})}&,\cos{(\alpha_{24})}\\\cos;-1&,\cos{(\alpha_{34})}\\\cos{(\alpha_{14})}&\cos{(\alpha_{34})}\cos{(\alpha_{23})}& \cos{(\alpha_{24})}&{(\alpha_{13})}&.&-1\\\end{vmatrix}}=0\,}$

여기서_ij α는 면 i와 j 사이의 각도이다.

정사면체의 꼭지점 위치 좌표의 기하학적 중앙값과 그 등각 중심은 삼각형에 대해 관측된 것과 유사한 상황에서 연관되어 있다.Lorenz Lindelöf는 주어진 사면체에 대응하는 점이 현재 등각 중심이라고 알려진 점이며, 면에 의해 기울어진 고체 각도가 동일하고, 공통값인 δ sr을 가지며, 반대쪽 모서리에 의해 기울어진 ^[25]각도가 동일하다는 것을 발견했다.고체각도 θ sr은 모든 공간에 의해 하위 처리된 것의 4분의 1이다.사면체 정점의 모든 고체 각도가 θ sr보다 작을 때, O는 사면체 안에 있고, O에서 정점까지의 거리의 합이 최소이기 때문에, O는 정점의 기하학적 중위수인 M과 일치한다.정점 중 하나에서의 입체각 v가 정확히 θ sr을 측정하면 O와 M이 v와 일치한다. 단, 사각형에 θ sr보다 큰 입체각을 가진 정점 v가 있다면 M은 여전히 v에 해당하지만 O는 사각형 밖에 있다.

기하 관계

사면체는 3-단순체이다.다른 플라톤계 고체의 경우와는 달리, 정4면체의 모든 정점은 서로 등거리이다(3차원 공간에서 4개의 등거리 점의 유일한 배열이다).

사면체는 삼각형 피라미드이고, 정사면체는 자기 쌍대이다.

정4면체는 각 정점이 정육면체의 정점이 되고 각 가장자리가 정육면체의 대각선이 되도록 2가지 방법으로 정육면체 내부에 삽입할 수 있다.이러한 매립의 경우, 정점의 데카르트 좌표는 다음과 같다.

(+1, +1, +1);

(−1, −1, +1);

(−1, +1, −1);

(+1, −1, −1).

그러면 원점을 중심으로 모서리 길이가 2⁄2인 사면체가 생성됩니다.다른 사면체(첫 번째와 이중)의 경우 모든 부호를 반대로 바꿉니다.이 두 사면체의 꼭지점은 정육면체의 꼭지점이며, 정사면체가 3데미큐브임을 보여준다.

이 사면체의 부피는 입방체의 3분의 1이다.두 사면을 결합하면 두 사면체 또는 스텔라 옥탄굴라의 화합물이라고 불리는 규칙적인 다면체 화합물이 생긴다.

스텔라 팔각형의 내부는 8면체이며, 이에 대응하여 정팔면체는 정팔면체에서 선형 크기의 절반인 4개의 정팔면체를 잘라낸 결과이다(즉, 정팔면체).

위의 매립은 입방체를 5개의 사면체로 나누고, 그 중 하나는 규칙적이다.사실 5는 큐브를 구성하는 데 필요한 사면체의 최소 수이다.이것을 보려면, 4개의 정점이 있는 기본 사면체에서 시작하여, 추가된 각 사면체는 최대 1개의 새로운 정점을 더합니다. 따라서 8개의 정점이 있는 입방체를 만들기 위해 적어도 4개를 더해야 합니다.

정육면체 5개의 정육면체 안에 사면체를 새겨넣으면 정육면체 5개와 정육면체 10개를 포함한 2개의 정육면체를 더 얻을 수 있다.

비록 이 결과는 아리스토텔레스가 가능하다고 주장했을 만큼 충분히 가능성이 있어 보이지만, 정사면체는 스스로 공간을 테셀링할 수 없다.그러나, 두 개의 정사면체는 8면체와 결합할 수 있으며, 공간을 사면체-팔면체 벌집처럼 타일링할 수 있는 마름모꼴을 제공한다.

그러나, 몇개의 불규칙한 사면체가 알려져 있으며, 그 복사본은 공간을 타일링할 수 있다.예를 들어 입방체의 특징적인 오르토셈과 디셰노이드 사면체 벌집체의 디셰노이드이다.리스트 전체가 해결되지 않은 채로 있다.^[26]

사면이 모두 같은 모양이어야 한다는 조건을 완화하면 사면체만을 사용하여 여러 가지 방법으로 공간을 타일링할 수 있다.예를 들어, 한 팔면체를 네 개의 동일한 사각형으로 나누고 두 개의 정면체와 다시 결합할 수 있다.(부록으로서 이 두 종류의 사면체는 같은 부피를 가지고 있습니다.

사면체는 평행면이 없다는 점에서 균일한 다면체 중에서 독특하다.

사면체의 사인 법칙과 사면체의 모든 형태의 공간

일반적인 사인 법칙의 결과는 정점 O, A, B, C가 있는 사면체에서 우리는

$\displaystyle \sin \angle OAB\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,}$

이 식별의 양면을 표면의 시계 방향과 시계 반대 방향으로 볼 수 있다.

4개의 꼭지점 중 하나를 O의 역할에 넣으면 4개의 동일성이 생성되지만, 그 중 3개는 독립적입니다. 만약 이들 중 3개의 "시계방향" 변이 곱해지고 곱이 같은 3개의 동일성의 "반시계방향" 변의 곱과 같다면, 그리고 나서 공통 인수가 양쪽에서 상쇄됩니다.결과는 네 번째 정체성입니다.

세 개의 각도는 합계가 180°(θ 라디안)인 경우에만 일부 삼각형의 각도입니다.어떤 12개의 각도가 어떤 사면체의 12개의 각도가 되기에 충분하고 필요한 조건은 무엇인가?분명히 사면체의 각도의 합은 180°이어야 한다.이러한 삼각형이 4개이므로 각도의 합계에 4개의 제약이 있어 자유도가 12개에서 8개로 감소한다.이 사인 법칙에 의해 주어진 4가지 관계는 자유도를 8에서 4가 아닌 5로 감소시킵니다. 왜냐하면 네 번째 제약조건은 처음 세 가지와 독립적이지 않기 때문입니다.따라서 모든 형태의 사면체 공간은 5차원이다.^[27]

사면체의 코사인 법칙

{P₁,P₂,P₃,P,P₄}를 사면체의 점이라고 하자.δ를_i 정점_i P와 반대되는 면의 면적, θ를_ij 모서리_ij PP에 인접한 사면체의 두 면 사이의 이면각으로 하자.

이 사면체의 ^[28]코사인 법칙은 정점 주위의 이면각과 사면체의 면적을 관련짓는 것으로, 다음과 같은 관계에 의해 주어진다.

$\displaystyle \Delta _{i}^{2}=\Delta _{j}^2}+\Delta _{l}^{2}-2(\Delta _{j}\cos \theta _{il}+\Delta\cos \cos \{l}) _{delta}$

내부점

P를 정점이 A, B, C, D이고 반대 면의 면적이_a F, F_bc, F인_d 부피 V의 사면체의 내부 점이라고 하자.그럼^{[29]: p.62, #1609} .

${\displaystyle PA\cdot F_{\mathrm {a}}+PB\cdot F_{\mathrm {b}}+PC\cdot F_{\mathrm {c}}+PD\cdot F_{\mathrm {d}}}\geq 9V}.$

꼭지점 A, B, C, D의 경우, 내부점 P 및 P에서 면까지의 수직의 발 J, K, L 및 M에 대해 면적이 동일하다고 가정한다^{[29]: p.226, #215} .

$(\display style PA+PB+)PC+PD\geq 3(PJ+PK+PL+PM).}$

인라디우스

i = 1, 2, 3, 4에 대해 사면체의 인반경을 r로, 삼각면의 인반경을 r로_i 나타내면, 다음과^{[29]: p.81, #1990} 같이 된다.

${{displaystyle {1}{r_{1}^{2}}+{\frac {1}{r_{2}^2}}+{\frac {1}{r_{3}^2}+{\frac {1}{r_{4}^2}}\leq {frac {frac {1}{frac {r}{r^2}}}}$

정사면체가 규칙적인 경우에만 동일한 값을 갖습니다.

A, A₂, A₃ 및 A가₄ 각 면의 면적을 나타내는 경우₁, r의 값은 다음과 같다.

$displaystyle$$\}\}\}\}\}.$

이 공식은 사면체를 4개의 사면체로 나누어 구하며, 사면체의 점은 원래 면 중 하나와 유인제의 세 점이 된다.4개의 서브테라면이 볼륨을 채우고 있으므로 V ${\displaystyle =}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{3}{}}$ ${\displaystyle {A\mathrm{}}_{}}$ ${\displaystyle {}_{}}$r + ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{3}{}}$ ${\displaystyle {A\mathrm{}}_{}}$ ${\displaystyle {}_{}}$r + ${\displaystyle \frac{1}{}}$ 3 ${\displaystyle A{}_{}}$ ${\displaystyle {3\mathrm{}}_{}{}_{}}$ + ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle 3{}_{}}$ ${\displaystyle {A\mathrm{}}_{}}$ 4$$ ({ $displaystyle$ V =$scapfrac {$1$}$ ${3}} A_{1}r$+ {1} $A_{2}r$+ {\$frac$ {} {$3}$ {3} A_frac} {3}} {A_frac} {$1{\displaystyle }$} {1} {1} {1} {1} {1} {1} {1} {1} {1} {1} {1} {1} {1} {1} {1} {$1$

서클라디우스

사면체의 반지름을 R로 나타냅니다.a, b, c는 정점에서 만나는 세 개의 가장자리의 길이, A, B, C는 반대쪽 가장자리의 길이라고 하자.V를 사면체의 부피라고 하자.그럼^[30][31].

${\displaystyle R=bfrac {(aA+bB+cC)(aA-bB+C)(-A+B+C)}}{24V}}.}$

원주점

사면체의 원주 중심은 세 개의 이등분면체의 교차점으로 찾을 수 있습니다.이등분선 평면은 사면체의 가장자리에 중심을 두고 직교하는 평면으로 정의된다.이 정의를 사용하면 정점₀ x,x₁,x₂₃,x를 갖는 사면체의 원심 C를 행렬 벡터 ^[32]곱으로 공식화할 수 있다.

$디스플레이 스타일C&=A^{-1}B&{\text{where}&\A=\left({\begin{matrix}\left[x_{1}-x_{0}\right]^{T}\\left[x_{2}-x_{0}\right]^{T}\\left[x_{3}-x_{0}\right]^{T}\end{matrix}\right}&\{\text{and}}&\B=sleftfrac {1}{2}-\x_{0}\x_{1}\^{2}-\x_{2}-\x_{0}\\x{2}-\x_{3}x_{2}\\\\\{2}$

중심과 대조적으로, 원주 중심이 항상 사면체 내부에 있는 것은 아닙니다.둔각 삼각형과 유사하게, 원주 중심은 둔각 사면체의 물체 밖에 있다.

중심

4면체의 질량 중심은 4개의 꼭지점에 대한 산술 평균으로 계산됩니다(중심 참조).

얼굴

세 면의 면적 합계가 네 번째 ^{[29]: p.225, #159} 면의 면적보다 큽니다.

정사면체

정수값 가장자리 길이, 면적 및 부피를 가진 사면체가 존재합니다.이것들은 헤로니아 사면체라고 불린다.한 예에서는 896의 한쪽 모서리, 990의 반대쪽 모서리, 1073의 다른 네 개의 모서리가 있습니다. 두 개의 면은 면적이 436800인 이등변 삼각형이고 다른 두 개의 면은 면적이 47120인 이등변 삼각형이며 볼륨은 124185600입니다.^[33]

사면체는 엣지로서 정수 부피와 연속 정수를 가질 수 있으며, 예를 들어 엣지 6, 7, 8, 9, 10, 11 및 볼륨 ^[34]48을 가진 것이 있다.

관련 다면체 및 화합물

정4면체는 삼각형 피라미드로 볼 수 있다.

일반 피라미드
디지털	삼각형의	광장	오각형의	육각형	칠각형의	팔각형의	에네오갈	십각형...
부적절한	규칙적인.	등변		이등분

정4면체는 축퇴 다면체, 즉 기본 다각형은 축퇴 다면체로 볼 수 있으며, 여기서 기본 다각형은 축퇴 다면체이다.

균일한 n-곤형 반프리즘

• v
• t

안티프리즘명	이원적 반대론	(트리거) 삼각 반체제	(사각형) 정사각형 반체제	오각반대론	육방정반대론	칠각반대론	팔각반대론	정방정반대론	십각반대론	헨데코날 반체제	도대각선 반대론	...	반인륜주의
다면체 이미지												...
구형 타일 이미지												평면 타일 이미지
정점 설정	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

정4면체는 축퇴 다면체로 볼 수 있으며, 두 세트의 공선 모서리에 6개의 정점을 포함하는 균일한 이중 삼면체이다.

n-곤형 트라페조헤드라과

삼면체 이름	이원삼면체 (4면체)	삼각삼면체	정방정삼면체	오각삼면체	육각삼면체	칠각삼면체	팔각삼면체	십각삼면	십이지각삼면체	...	편평형 삼면체
다면체 이미지										...
구형 타일 이미지										평면 타일 이미지
얼굴 구성	V2.3.3	V3.3.3	V4.3.3	V5.3.3	V6.3.3	V7.3.3	V8.3.3	V10.3.3	V12.3.3	...	V4.3.3

사면체에 적용된 절단 과정은 일련의 균일한 다면체를 생성한다.모서리를 점으로 잘라내면 8면체가 정류된 사면체로 생성됩니다.프로세스는 양방향으로 완료되어 원래 면을 점으로 줄이고 다시 한 번 자기 이중 사면체를 생성합니다.

균일한 사면체 다면체군
대칭: [3,3], (*332)							[3,3]+, (332)
{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
이중에서 균일한 다면체
V3.3.3	V3.6.6	V3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3

이 다면체는 쌍곡면으로 이어지는 슐레플리 기호 {3,n}을 가진 정다면체의 수열의 일부로서 위상적으로 관련되어 있다.

*n32 정규타일링 대칭변환: {3,n} v t
구면				유클리드	콤팩트 하이퍼		파라코	비콤팩트 쌍곡선
3.3	3개3	3개4	3개5	3개6	3개7	3개8	3개∞	3개12i	3개9i	3개6i	3개3i

사면체는 정점 도형이 3차인 일련의 정다면체와 타일링과 위상적으로 관련되어 있습니다.

*n32 정규 타일링 대칭 변환: {n,3} v t
구면				유클리드	콤팩트 쌍곡선		파라코	비콤팩트 쌍곡선
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

• 사면체 화합물
• 

  정육면체 두 개

• 

  5개의 사면체 화합물

• 

  10개의 사면체 화합물

흥미로운 다면체는 교차하는 5개의 사면체로부터 구성될 수 있다.이 5개의 사면체 화합물은 수백 년 동안 알려져 왔다.종이접기의 세계에 정기적으로 등장합니다.20개의 꼭지점을 결합하면 정십이면체가 된다.왼손잡이와 오른손잡이의 형태가 있는데, 이것은 서로의 거울 이미지이다.두 형태를 겹치면 10개의 사면체 화합물이 되고, 10개의 사면체가 5쌍의 팔각체로 배열된다.스텔라 팔각형은 이중 위치에 있는 두 개의 사각형으로 이루어진 화합물이며, 그것의 8개의 꼭지점은 볼록한 선체로 큐브를 정의합니다.

정사각형 호소면체는 네 개의 면을 가진 또 다른 다면체이지만 삼각형 면을 가지고 있지는 않다.

실라시 다면체와 사면체는 각 면이 서로 가장자리를 공유하는 것으로 알려진 유일한 두 개의 다면체이다.게다가, CsaaSzarr 다면체(그 자체가 Silassi 다면체의 쌍체)와 사면체는 모든 대각선이 변에 있는 것으로 알려진 유일한 두 개의 다면체이다.

적용들

수치 분석

수치해석학에서 복잡한 3차원 형상은 특히 편미분방정식의 수치해법에서 유한요소해석을 위한 방정식을 설정하는 과정에서 일반적으로 불규칙 사면체의 다각형 메시로 분해되거나 근사된다.이 방법들은 컴퓨터 유체 역학, 공기역학, 전자기장, 토목 공학, 화학 공학, 해군 건축 및 공학 및 관련 분야 및 관련 분야에서 실용적으로 광범위하게 응용된다.

구조 공학

단단한 모서리를 가진 사면체는 본질적으로 강체이다.이러한 이유로 스페이스 프레임과 같은 프레임 구조를 강화하는 데 자주 사용됩니다.

항공

일부 비행장에서는 회전하는 피벗 위에 얇은 재료로 덮인 2면을 가진 사면체 모양의 큰 프레임이 장착돼 항상 바람을 향한다.그것은 공중에서 볼 수 있을 정도로 크게 지어졌고 때때로 조명이 켜진다.그 목적은 풍향을 ^[35]나타내는 조종사를 참조하는 것이다.

화학

사면체 모양은 자연에서 공유 결합 분자에서 볼 수 있다.모든 sp-하이브리드³ 원자는 사면체의 네 모서리에서 원자(또는 단일 전자 쌍)로 둘러싸여 있다.예를 들어 메탄 분자(CH
₄) 또는 암모늄 이온(NH⁺
₄)에서는 4개의 수소 원자가 중앙 탄소 또는 질소 원자를 사면체 대칭으로 둘러싸고 있다.이러한 이유로, 유기 화학의 선도적인 저널 중 하나는 사면체라고 불립니다.완벽한 사면체의 두 꼭지점 사이의 중심 각도는 아크코스(-1/3) 즉, 약 109.47°^[5]이다.

물, HO는
₂ 또한 중심 산소 원자 주위에 두 개의 수소 원자와 두 쌍의 전자가 있는 사면체 구조를 가지고 있습니다.그러나 그 사면체 대칭은 단일 쌍이 단일 O-H 결합보다 더 많이 밀어내기 때문에 완벽하지 않다.

화학물질 혼합의 4차 위상도는 사면체로서 그래픽으로 표현된다.

단, 통신공학의 4차 위상도는 2차원 평면상에 그래프로 표현된다.

전기전자제품

6개의 동일한 저항을 함께 납땜하여 사면체를 형성하면 두 정점 사이에서 측정된 저항은 1개의 ^[36][37]저항의 절반입니다.

실리콘은 고체 전자제품에 가장 많이 사용되는 반도체이고 실리콘은 4가자의 원자가이기 때문에 실리콘에 있는 4개의 화학결합의 사면체 형상은 실리콘의 결정이 어떻게 형성되고 어떤 형태를 띠는지에 큰 영향을 미친다.

색공간

사면체는 특히 휘도축이 색공간을 대각선으로 분할하는 경우에 색공간 변환 알고리즘에 사용된다(예를 들어 RGB, CMY).^[38]

게임.

기원전 2600년부터 시작된 우르의 왕실 게임은 사면체 주사위 세트로 진행되었다.

특히 롤플레잉에서, 이 고체는 4면 다이스로 알려져 있는데, 이 다면체 주사위 중 하나이며, 굴린 숫자는 하단 또는 상단 정점에 나타난다.피라밍크스나 피라몰픽스와 같은 몇몇 루빅스 큐브 같은 퍼즐은 사면체이다.

지질학

지구의 ^[39]형성을 설명하기 위해 윌리엄 로션 그린이 원래 발표한 사면체 가설은 20세기 ^[40][41]초에 유행했다.

무기

일부 칼트롭은 착지 방법과 상관없이 하나의 스파이크가 위로 향하기 때문에 사면을 기반으로 하며 두 개의 구부러진 못을 용접하여 쉽게 만들 수 있습니다.

현대 미술

오스트리아의 예술가 마르티나 셰티나는 형광등을 사용하여 4면체를 만들었습니다.그것은 오스트리아 2010 ^[42]라이트 아트 비엔날레에서 전시되었다.

그것은 머드베인의 모든 것의 종말에서 검은 불꽃으로 둘러싸인 앨범 예술작품으로 사용된다.

대중문화

인지 과학자이자 인공지능 전문가인 마빈 민스키에 따르면 스탠리 큐브릭은 원래 2001년에 모노리스인 우주 오디세이를 4면체로 만들려 했다. 그는 큐브릭에게 HAL 9000 컴퓨터와 영화의 다른 측면에 대해 조언했다.큐브릭은 이 4면체를 보는 방문객이 그것이 무엇인지 인식하지 못하며 일반인들이 이해하지 ^[43]못하는 영화 속 어떤 것도 원하지 않기 때문에 그 4면체를 사용한다는 아이디어를 폐기했다.

사면체 그래프

사면체 그래프
꼭지점	4
가장자리	6
반지름	1
직경	1
둘레	3
자기동형	24
색수	4
특성.	해밀턴, 정규, 대칭, 거리-정규, 거리-추이, 3-vertex 연결, 평면 그래프
그래프 및 매개 변수 표

정점과 모서리를 구성하는 사면체의 골격은 4개의 정점과 6개의 모서리를 가진 그래프를 형성합니다.이것은 완전한 그래프 K와₄ 휠 그래프₄ ^[44]W의 특수한 경우입니다. 이것은 5개의 플라톤 그래프 중 하나이며, 각각 플라톤 고체의 골격입니다.

삼배 대칭

「 」를 참조해 주세요.

• 보어다이크-콕서터 나선
• 뫼비우스 설정
• 칼트롭
• Demihypercube 및 Simplex – n차원 아날로그
• 펜타코론 – 4차원 아날로그
• 시너지 효과(풀러)
• 사면체 연
• 사면체수
• 사면체 패킹
• 삼각 쌍방향체 – 한 면을 따라 두 개의 사면체를 접합하여 제작됨
• 삼각형 사면체
• 오르토셈

메모들

레퍼런스

참고 문헌

• Kepler, Johannes (1619). Harmonices Mundi (The Harmony of the World). Johann Planck.
• Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.

외부 링크

• Weisstein, Eric W. "Tetrahedron". MathWorld.
• 사면체 및 기타 많은 다면체의 무료 종이 모형
• "사면체의 회전 고리"에 대한 설명도 포함된 놀라운 공간 채우기 비정규 사면체입니다. 케일리도 사이클이라고도 합니다.

v t 치수 2-10의 기본 볼록 정규 및 균일한 폴리토프
가족	An	Bn	I2(p) / Dn	E6/E7/E8/F4/G2	Hn
정다각형	삼각형	광장	p곤	육각형	펜타곤
균일한 다면체	사면체	8면체 • 큐브	데미큐브		12면체 • 이십면체
균일한 폴리코론	펜타코론	16 셀 • 테서랙트	데모테서랙트	24 셀	120 셀 • 600 셀
균일한 5 폴리토프	51200x	5 - ORTOPLEX • 5 - 큐브	5 데미큐브
균일한 6 폴리토프	61200x	6-정류 • 6-큐브	6-데미큐브	122 • 221
균일한 7 폴리토프	71200x	7-정류 • 7-큐브	7 데미큐브	132 • 231 • 321
균일한 8 폴리토프	8180x	8-정류 • 8-큐브	8개의 데미큐브	142 • 241 • 421
균일한 9-폴리토프	9169x	9-정류 • 9-입방체	9데미큐브
균일한 10 폴리토프	10-1996x	10 - ORTOPLEX • 10 - 큐브	10 데미큐브
균일한 n-폴리토프	n-1996x	n-ortoplex • n-입방체	n-데미큐브	1k2 • 2k1 • k21	n-오각형 폴리토프
주제: 폴리토프 패밀리 • 일반 폴리토프 • 일반 폴리토프 및 화합물 목록