Wenninger 다면체 모델 목록

이것은 Magnus Wenninger의 저서 Polyhedron Models에 수록된 유니폼과 스티로잉된 폴리헤드라의 색인 목록이다.

이 책은 다면체를 물리적 모델로 만드는 지침서로 쓰여졌다.그것은 건축을 위한 얼굴 요소들의 템플릿과 건축에 도움이 되는 힌트를 포함하고 있으며, 또한 이러한 형상들의 이면에 있는 이론에 대한 간단한 설명도 포함하고 있다.75개의 비수정복 다면체뿐만 아니라 44개의 강선 형태의 볼록정규 다면체도 함유하고 있다.

여기에 열거된 모델은 "Wenninger Model N번" 또는 간결성을 위한 W로_N 인용할 수 있다.

다면체는 5개의 표로 그룹화된다.정규(1–5), 세미레그룰라(6–18), 정규 항성 폴리헤드라(20–22,41), 스텔레이션스 및 화합물(19–66) 및 균일한 항성 폴리헤드라(67–119).4개의 일반 별 다면체는 균일한 다면체 그룹과 석면 그룹에 모두 속하기 때문에 두 번 나열된다.

플라톤 고형분(일반 볼록 다면체) W1 ~ W5

색인	이름	사진	이중명	듀얼 픽처	와이토프 기호	정점수 슐래플리 기호	대칭군	U#	K#	V	E	F	유형별 면
1	사면체		사면체		3 2 3	{3,3}	Td	U01	K06	4	6	4	4{3}
2	팔면체		육면체		4 2 3	{3,4}	Oh	U05년	K10	6	12	8	8{3}
3	육면체(큐브)		팔면체		3 2 4	{4,3}	Oh	U06	K11	8	12	6	6{4}
4	이코사헤드론		도데카헤드론		5 2 3	{3,5}	Ih	U22	K27	12	30	20	20{3}
5	도데카헤드론		이코사헤드론		3 2 5	{5,3}	Ih	U23	K28	20	30	12	12{5}

아르키메데스 고형분(세미레굴러) W6~W18

색인	이름	사진	이중명	듀얼 픽처	와이토프 기호	정점수	대칭군	U#	K#	V	E	F	유형별 면
6	잘린 사면체		삼면체		2 3 3	3.6.6	Td	U02년	K07	12	18	8	4{3} + 4{6}
7	잘린 팔면체		테트라키스 육면체		2 4 3	4.6.6	Oh	U08년	K13	24	36	24	6{4} + 8{6}
8	잘린 육면체		삼면체		2 3 4	3.8.8	Oh	U09	K14	24	36	14	8{3} + 6{8}
9	잘린 이코사면체		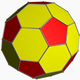펜타키스 도데면체		2 5 3	5.6.6	Ih	U25	K30	60	90	32	12{5} + 20{6}
10	잘린 도두면체		삼면체		2 3 5	3.10.10	Ih	U26	K31	60	90	32	20{3} + 12{10}
11	큐폭타헤드론		진드기 도데면체		2 3 4	3.4.3.4	Oh	U07	K12	12	24	14	8{3} + 6{4}
12	이코시다데카헤드론		3면체		2 3 5	3.5.3.5	Ih	U24	K29	30	60	32	20{3} + 12{5}
13	소형 롬비큐옥타헤드론		살상성 이코시테트라헤드론		3 4 2	3.4.4.4	Oh	U10	K15	24	48	26	8{3}+(6+12){4}
14	소형 롬비코시도데카헤드론		망상 육면체		3 5 2	3.4.5.4	Ih	U27	K32	60	120	62	20{3} + 30{4} + 12{5}
15	잘린 큐옥타헤드론 (위대한 롬비큐보옥타헤드론)		이디야키스 도데카헤드론		2 3 4	4.6.8	Oh	U11	K16	48	72	26	12{4} + 8{6} + 6{8}
16	잘린 이코시다데카헤드론 (위대한 롬비코시도데카헤드론)		이디야키스 삼권면체		2 3 5	4.6.10	Ih	U28	K33	120	180	62	30{4} + 20{6} + 12{10}
17	스너브 큐브		오각형 이코시테트라헤드론		2 3 4	3.3.3.3.4	O	U12	K17	24	60	38	(8 + 24){3} + 6{4}
18	스너브 도데카헤드론		오각 육면체		2 3 5	3.3.3.3.5	I	U29	K34	60	150	92	(20 + 60){3} + 12{5}

케플러-푸인소트 다면체(일반 항성 다면체) W20, W21, W22 및 W41

색인	이름	사진	이중명	듀얼 픽처	와이토프 기호	정점수 슐래플리 기호	대칭군	U#	K#	V	E	F	유형별 면
20	소절개도면체		대두면체		5 25/2	{5/2,5}	Ih	U34	K39	12	30	12	12{5/2}
21	대두면체		소절개도면체		5/2 2 5	{5,5/2}	Ih	U35	K40	12	30	12	12{5}
22	그레이트 스틸 도데카헤드론		대이코사면체		3 25/2	{5/2,3}	Ih	U52	K57	20	30	12	12{5/2}
41	대이코사면체 (제16회 이코사면체)		그레이트 스틸 도데카헤드론		5/2 2 3	{3,5/2}	Ih	U53년	K58	12	30	20	20{3}

Stellations: W19 ~ 66 모델

팔면체

색인	이름	대칭군	사진	면
2	팔면체 (정규직)	Oh
19	스텔라화옥타헤드론 (두 개의 4면체 조합)	Oh

도데카헤드론 기단

색인	이름	대칭군	사진	면
5	도데카헤드론(정기)	Ih
20	소절개도면체(정기) (도데카헤드론 1호)	Ih
21	대두면체(정기) (두 번째 도데카헤드론)	Ih
22	그레이트 스틸 도데카헤드론(정기) (도데카헤드론 제3기)	Ih

이코사헤드론 기단

색인	이름	대칭군	사진	면
4	이코사헤드론(정기)	Ih
23	5옥타헤드라 화합물 (이코사헤드론의 첫 번째 복합도장)	Ih
24	5개의 사면체 화합물 (이코사면체의 두 번째 복합면도)	I
25	사면체 10개 화합물 (이코사헤드론의 세 번째 복합도장)	Ih
26	작은삼각형 이코사면체 (이코사면체 1호) (트리아키스 이코사면체)	Ih
27	이코사헤드론 제2기각	Ih
28	발굴된 도데면체 (이코사헤드론 제3기)	Ih
29	제4회 이코사면체	Ih
30	이코사헤드론 제5기각	Ih
31	이코사헤드론 제6호 봉합	Ih
32	제7회 이코사면체	Ih
33	제8회 이코사면체	Ih
34	제9회 이코사면체 대삼면체	Ih
35	이코사헤드론 제10기	I
36	이코사면체의 열한번째 절개	I
37	이코사헤드론 제12기	Ih
38	이코사헤드론 13호 봉합	I
39	이코사헤드론 14도	I
40	이코사면체 15도	I
41	대이코사면체(정기) (이코사면체 16도)	Ih
42	이코사면체 최종면도	Ih

큐옥타헤드론 석회화

색인	이름	대칭군	사진	면(옥타헤드럴 평면)	면(큐브 평면)
11	큐폭타헤드론(정기)	Oh
43	큐브와 팔면체의 화합물 (제1차 큐옥타헤드론)	Oh
44	큐옥타헤드론 제2호	Oh
45	큐옥타헤드론 제3기	Oh
46	큐옥타헤드론 제4기	Oh

이코시다데카헤드론 기단

색인	이름	대칭군	사진	면(동측면)	면(도면 평면)
12	이코시다데카헤드론 (정규직)	Ih
47	(이코시다데카헤드론 1호) 도데면체와 이코사면체의 화합물	Ih
48	이코시다데카헤드론 제2기각화	Ih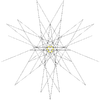
49	이코시다데카헤드론 제3기	Ih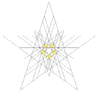
50	이코시다데카헤드론 제4기 (소형 강판 도데카헤드론 혼용) 그리고 삼위일체(삼두정맥)	Ih
51	이코시다데카헤드론 제5도장 (소형 강판 도데카헤드론 혼용) 및 5옥타헤드라)	Ih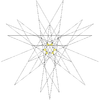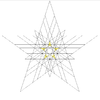
52	제6회 이코시다데카헤드론 기법	Ih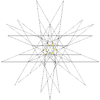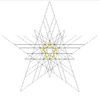
53	이코시다데카헤드론 제7기	Ih
54	이코시다데카헤드론 제8기 (5개의 4면체 혼합물) 그리고 위대한 도두면체)	I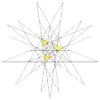
55	이코시다데카헤드론 제9기	Ih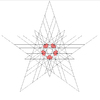
56	이코시다데카헤드론 제10호 봉합	Ih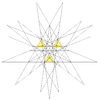
57	이코시다데카헤드론 열한번째 스텔링	Ih
58	이코시다데카헤드론 제12기	Ih
59	이코시다데카헤드론 제13호 봉합	Ih
60	이코시다데카헤드론 열네번째 절개	Ih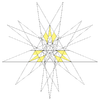
61	대절개면체와 대절개면체의 화합물	Ih
62	이코시다데카헤드론 15도	Ih
63	제16회 이코시다데카헤드론 강판	Ih
64	이코시다데카헤드론 제17기	Ih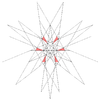
65	제18회 이코시다데카헤드론 강판	Ih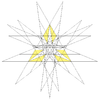
66	제19회 이코시다데카헤드론 기법	Ih

균일한 비콘벡스 솔리드 W67 ~ W119

색인	이름	사진	이중명	듀얼 픽처	와이토프 기호	정점수	대칭군	U#	K#	V	E	F	유형별 면
67	테트라헤미헥사헤드론		테트라헤미헥사크론		3/23 2	4.3/2.4.3	Td	U04	K09	6	12	7	4{3}+3{4}
68	옥타헤미오크타헤드론		옥타헤미옥타크론		3/23 3	6.3/2.6.3	Oh	U03년	K08	12	24	12	8{3}+4{6}
69	소형입방옥타헤드론		소형 육각형 이코시트라헤드론		3/24 4	8.3/2.8.4	Oh	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	소형 이코시다데카헤드론		작은삼각형 이코사면체		3 5/23	(5/2.3)3	Ih	U30	K35	20	60	32	20{3}+12{5/2}
71	작은이코시도데카헤드론		소형 이코사크로닉 육면체		5/23 3	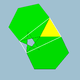6.5/2.6.3	Ih	U31	K36	60	120	52	20{3}+12{5/2}+20{6}
72	소도데키도데코데카헤드론		소형 도데카크로닉 육면체		3/25 5	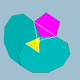10.3/2.10.5	Ih	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	도데카데카헤드론		중합성삼정면체		2 5/25	(5/2.5)2	Ih	U36	K41	30	60	24	12{5}+12{5/2}
74	소형 롬비도데카헤드론		소형 롬비도데카크론		25/25	10.4.10/9.4/3	Ih	U39	K44	60	120	42	30{4}+12{10}
75	잘린 대두면체		작은 돌기둥 도데카헤드론		25/2 5	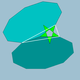10.10.5/2	Ih	U37	K42	60	90	24	12{5/2}+12{10}
76	롬비도데코데카헤드론		육면체성 망상증면체		5/25 2	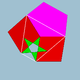4.5/2.4.5	Ih	U38	K43	60	120	54	30{4}+12{5}+12{5/2}
77	대입방옥타헤드론		대육각형 이코시트라헤드론		3 4 4/3	8/3.3.8/3.4	Oh	U14	K19	24	48	20	8{3}+6{4}+6{8/3}
78	큐보헤미오크타헤드론		헥사헤미옥타크론		4/34 3	6.4/3.6.4	Oh	U15	K20	12	24	10	6{4}+4{6}
79	큐비트런드 큐빅토크헤드론 (Cuboctatrun cuboctatrun cuboctaheadron)		테트라디야키스 육면체		4/33 4	8/3.6.8	Oh	U16	K21	48	72	20	8{6}+6{8}+6{8/3}
80	직교 도데코데카헤드론		중삼면체		3 5/35	(5/3.5)3	Ih	U41년	K46	20	60	24	12{5}+12{5/2}
81	대디트리곤 도디코시도데카헤드론		대직류도데카크로닉 육각면체		3 5 5/3	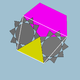10/3.3.10/3.5	Ih	U42년	K47	60	120	44	20{3}+12{5}+12{10/3}
82	소두구체도치데카헤드론		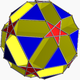소형 직류 도데카크로닉 육각면체		5/33 5	10.5/3.10.3	Ih	U43년	K48	60	120	44	20{3}+12{5/2}+12{10}
83	이코시다데코데카헤드론		메디알 이코사크로닉 헥스테콘헤드론		5/35 3	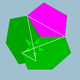6.5/3.6.5	Ih	U44	K49	60	120	44	12{5}+12{5/2}+20{6}
84	이코시트룬말살도데코헤드론 (이코시도데카트룬갈린이코시도데카헤드론)		삼디야키스 이코사면체		5/33 5	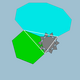10/3.6.10	Ih	U45	K50	120	180	44	20{6}+12{10}+12{10/3}
85	비콘벡스 대롬비쿠옥타헤드론 (Quasirhombicuboctaheadron)		대망상 이코시트라헤드론		3/24 2	4.3/2.4.4	Oh	U17	K22	24	48	26	8{3}+(6+12){4}
86	작은 rhombihexahedron		작은 rhombihexacron		3/22 4	4.8.4/3.8	Oh	U18	K23	24	48	18	12{4}+6{8}
87	대직류 이코시다데카헤드론		대삼면체		3/2 3 5	(5.3.5.3.5.3)/2	Ih	U47	K52	20	60	32	20{3}+12{5}
88	대이코시토다이데코헤드론		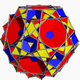대이코사크로닉 육면체		3/25 3	6.3/2.6.5	Ih	U48년	K53	60	120	52	20{3}+12{5}+20{6}
89	소이코시헤미도데코헤드론		소이코시헤미도데카크론		3/23 5	10.3/2.10.3	Ih	U49	K54	30	60	26	20{3}+6{10}
90	소십면체		소도데키코사크론		3/23 5	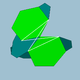10.6.10/9.6/5	Ih	U50	K55	60	120	32	20{6}+12{10}
91	소도데카헤미도데코헤드론		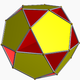작은도데카헤미도데카크론		5/45 5	10.5/4.10.5	Ih	U51년	K56	30	60	18	12{5}+6{10}
92	잘린 육면체 (정량 처리된 육면체)		대삼각형		2 3 4/3	8/3.8/3.3	Oh	U19	K24	24	36	14	8{3}+6{8/3}
93	잘린 큐옥타헤드론 (Quasitrunced cuboctaheadron)		대디야키 도데카헤드론		4/32 3	8/3.4.6	Oh	U20	K25	48	72	26	12{4}+8{6}+6{8/3}
94	대이코시다데카헤드론		대범삼문자		2 5/23	(5/2.3)2	Ih	U54년	K59	30	60	32	20{3}+12{5/2}
95	잘린 대 이코사면체		그레이트 스틸라펜타키스 도데카헤드론		25/2 3	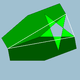6.6.5/2	Ih	U55	K60	60	90	32	12{5/2}+20{6}
96	롬비코사헤드론		롬비코사크론		25/23	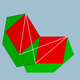6.4.6/5.4/3	Ih	U56	K61	60	120	50	30{4}+20{6}
97	잘린 작은 도데면체 (Quasitrunced small stelled dodecheadron)		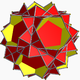대 펜타키스 도데카헤드론		2 5 5/3	10/3.10/3.5	Ih	U58년	K63	60	90	24	12{5}+12{10/3}
98	잘린 도데코데카헤드론 (Quasitrunculated dodecheadron)		중형 이디다키스 삼정면체		5/32 5	10/3.4.10	Ih	U59년	K64	120	180	54	30{4}+12{10}+12{10/3}
99	대식도데코데카헤드론		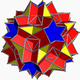그레이트 도데카크로닉 육면체		5/23 5/3	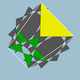10/3.5/2.10/3.3	Ih	U61	K66	60	120	44	20{3}+12{5/2}+12{10/3}
100	작은 도데카헤미코사헤드론		소도데카헤미코사크론		5/35/2 3	6.5/3.6.5/2	Ih	U62년	K67	30	60	22	12{5/2}+10{6}
101	대반면체		그레이트 도데시코사크론		5/35/23	6.10/3.6/5.10/7	Ih	U63년	K68	60	120	32	20{6}+12{10/3}
102	도데카헤미코사헤드론		그레이트 도데카헤미코사크론		5/45 3	6.5/4.6.5	Ih	U65	K70	30	60	22	12{5}+10{6}
103	대록비헥사헤드론		대록비헥사크론		4/33/22	4.8/3.4/3.8/5	Oh	U21	K26	24	48	18	12{4}+6{8/3}
104	대절개 자른 도데카헤드론 (Quasitrunced great stelled dodecheadron)		대삼면체		2 3 5/3	10/3.10/3.3	Ih	U66	K71	60	90	32	20{3}+12{10/3}
105	비콘벡스 대롬비코시도데카헤드론 (Quasirhombicosidodecahedron)		대망상 육면체		5/33 2	4.5/3.4.3	Ih	U67년	K72	60	120	62	20{3}+30{4}+12{5/2}
106	대이코시헤미도데코헤드론		대이코시헤미도데카크론		3 3 5/3	10/3.3/2.10/3.3	Ih	U71년	K76	30	60	26	20{3}+6{10/3}
107	대 도데카헤미도데코헤드론		그레이트 도데카헤미도데카크론		5/35/2 5/3	10/3.5/3.10/3.5/2	Ih	U70	K75	30	60	18	12{5/2}+6{10/3}
108	크게 잘린 이코시다데카헤드론 (위대한 퀘이시트론경화 이코시다데카헤드론)		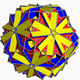대디야키스 삼관면체		5/32 3	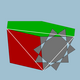10/3.4.6	Ih	U68년	K73	120	180	62	30{4}+20{6}+12{10/3}
109	대롬비도데카헤드론		그레이트롬비도데카크론		3/25/32	4.10/3.4/3.10/7	Ih	U73년	K78	60	120	42	30{4}+12{10/3}
110	소형 스너브 아이코시도데코헤드론		작은 육각형 육면체		5/23 3	3.3.3.3.3.5/2	Ih	U32	K37	60	180	112	(40+60){3}+12{5/2}
111	스너브 도데코데카헤드론		내측 오각형 육면체		25/25	3.3.5/2.3.5	I	U40	K45	60	150	84	60{3}+12{5}+12{5/2}
112	스너브 이코시다데코데카헤드론		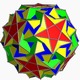내측 육각 육각형 육면체		5/33 5	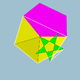3.3.3.3.5.5/3	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{5/2}
113	대역반입형 이코시도데카헤드론		대 역오각형 육면체		5/32 3	3.3.3.3.5/3	I	U69년	K74	60	150	92	(20+60){3}+12{5/2}
114	역 스너브 도데코데카헤드론		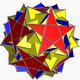내적 역오각형 육면체		5/32 5	3.5/3.3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{5/2}
115	그레이트 스너브 도데시코시도데카헤드론		대육각형 육면체		5/35/23	3.5/3.3.5/2.3.3	I	U64년	K69	60	180	104	(20+60){3}+(12+12){5/2}
116	대스너브 이코시다데코헤드론		대오각형 육면체		25/25/2	3.3.3.3.5/2	I	U57년	K62	60	150	92	(20+60){3}+12{5/2}
117	대환영 이코시다데카헤드론		대 펜타그램 육면체		3/25/32	(3.3.3.3.5/2)/2	I	U74년	K79	60	150	92	(20+60){3}+12{5/2}
118	작은 리콜루브 이코시도데체헤드론		작은 육각형 육면체		3/23/25/2	(3.3.3.3.3.5/2)/2	Ih	U72년	K77	180	60	112	(40+60){3}+12{5/2}
119	대디롬비코시도데카헤드론		대디롬비코시도데카크론		3/25/335/2	(4.5/3.4.3.4.5/2.4.3/2)/2	Ih	U75	K80	60	240	124	40{3}+60{4}+24{5/2}

참고 항목

• 균일한 다면체 목록
• 59 이코사헤드라
• 다면체 스텔링 목록

참조

• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
  • 에라타
    • Wenninger에서 W90의 정점 수치는 평행 모서리를 갖는 것으로 잘못 표시된다.
• Wenninger, Magnus (1979). Spherical Models. Cambridge University Press. ISBN 0-521-29432-0.

외부 링크

• 마그너스 J. 웬닝거
• 이 문서에서 이미지를 생성하는 데 사용되는 소프트웨어:
  • 스텔라: 폴리헤드론 네비게이터 스텔라(소프트웨어) - 웬닝거의 모든 다면 모델을 위한 그물을 만들고 인쇄할 수 있다.
  • 블라디미르 불라토프의 폴리헤드라 스틸레이션 애플릿
  • OS X 애플리케이션으로 패키지된 Vladimir Bulatov의 Polyedra Stellations Applet
• M. Wenninger, Polyhedron Models, Erata: 다양한 판의 알려진 오류.