입체각

입체각
입체각
공통 기호	Ω
SI 단위	스테라디안
기타 유닛	제곱도
SI 기준 단위	m2/m2
보존?	아니요.
파생상품; 기타 수량
치수

기하학에서 솔리드 각도(기호: $δ$ )는 주어진 물체가 커버하는 특정 지점에서 시야의 양을 측정하는 것입니다.즉, 그 시점에서 바라본 관찰자에게 물체의 크기를 나타내는 척도입니다.물체가 보이는 지점을 솔리드 각도의 정점이라고 하며, 이 물체는 그 지점으로부터 솔리드 각도의 정점이라고 합니다.

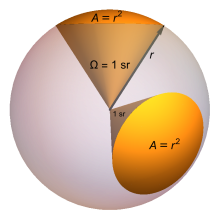
국제 단위계(SI)에서 입체각은 스테라디안(기호: sr)이라 불리는 무차원 단위로 표현된다.스테라디안 1개는 정점을 둘러싼 단위구상의 면적 1단위에 해당하므로 정점에서 나오는 모든 광선을 차단하는 물체는 단위구체의 총 $4\pi$ 과 동일한 수의 스테라디안 $(\displaystyle$ 4 $\pi$ 를 커버한다. 입체각은 도, 분, a와 같은 각도 측정의 제곱으로 측정할 수 있다.nd 초수

근처에 있는 작은 물체는 더 멀리 있는 큰 물체와 같은 입체각을 기울일 수 있습니다.예를 들어, 달은 태양보다 훨씬 작지만, 지구에 훨씬 더 가깝기도 하다.실제로, 지구의 어느 지점에서나 볼 수 있는 두 물체는 겉으로 보이는 크기뿐만 아니라 거의 같은 입체각을 가지고 있다.이것은 일식 동안 명백하다.

정의 및 속성

스테라디안 단위의 물체의 솔리드 각도는 물체가 덮는 단위 구면의 정점 중심 영역과 동일합니다.스테라디안에서의 입체 각도는 단위 구체의 세그먼트 면적과 동일하며 라디안에서의 평면 각도는 단위 원의 호 길이와 동일하다.따라서 라디안에서의 평면 각도가 반지름에 대한 원호 길이의 비율인 것처럼 스테라디안에서의 입체 각도는 다음과 같은 비율이다.

(\displaystyle \Omega = flac {A}{r^{2}})

여기서 A는 구형 표면적이고 r은 고려된 구의 반지름이다.

입체각은 종종 천문학, 물리학, 그리고 특히 천체 물리학에서 사용된다.매우 멀리 있는 물체의 입체 각도는 거리 제곱에 대한 면적 비율에 거의 비례합니다.여기서 "영역"은 보는 방향을 따라 투영될 때 물체의 영역을 의미합니다.

중심에서 관찰할 때 반지름의 제곱과 면적이 같은 구상의 영역은 정확히 한 스테라디안이다.

내부 어느 지점에서나 측정한 구의 고체 각도는 4µsr이고, 면 중 하나에 의해 큐브의 중심에서 기울어진 고체 각도는 그 1/6이다.2µ/3sr.고체 각도는 평방 도(1 sr = (180/ $sr$ )² 평방 도), 평방 분 및 평방 초 또는 스패트(1 sp = 4µ sr)라고도 하는 구의 일부(1 sr = 1/4µ 부분 면적)로 측정할 수 있습니다.

구면 좌표에는 미분 공식이 있다.

\displaystyle d\Omega =\sin \theta \,d\theta \,d\varphi ,}

여기서 $θ$ 는 결찰도( $북극$ 으로부터의 각도)이고 θ는 경도이다.

$점$ P에서 기울어진 임의의 방향 $표면$ S의 솔리드 각도는 표면 $S$ 가 중앙 $P$ 를 가진 단위 구에 투영되는 솔리드 각도와 같으며, 표면 적분으로 계산될 수 있습니다.

\Omega =\iint _{S}{\frac {r}}\cdot {r^{2}},dS\=\iint _{S}\sin \theta 、,d\theta 、,d\varphi

${\hat {r}}={\vec {r}}/r$ 서 r ${\hat {r}}={\vec {r}}/r$ ^ ${\hat {r}}={\vec {r}}/r$ ${\hat {r}}={\vec {r}}/r$ ${\hat {r}}={\vec {r}}/r$ / ${\hat {r}}={\vec {r}}/r$ ${\displaystyle$ { $r}$ = $r\$ displayvec ${r}/r$ }은 ${\hat {r}}={\vec {r}}/r$ r $→$ {\ $displaystyle {r$ 에 ${\vec {r}}$ 하는 단위 벡터이며, $여기$ 서 $^$ { $displaystyle {r}/$ r}은 $D$ 에 대한 단위 벡터를 나타냅니다 ${\hat {n}}$ .단위구상의 $표면S$ 에 대한 돌기가 동형이 아니더라도 스칼라 ${\hat {r}}\cdot {\hat {n}}$ r^^ ${\hat {r}}\cdot {\hat {n}}$ $^$ ${ style$ { $r}\cdot$ {n $}$ 기호로 기술된 표면방향에 따라 여러 개의 접힘을 올바르게 고려한다.

따라서 평면적 $dS$ , ${\hat {n}}$ n $^$ {\ $style {n$ 및 뷰어와의 $거리$ r을 가진 작은 면으로 기울어진 입체 각도를 다음과 같이 근사할 수 있습니다.

({displaystyle d\Omega = 4\pi \leftfrac {dS} {A}}\right}, ({\hat {n}}),

여기서 구의 표면적은 $A$ = $4µr$ 이다².

실용적인 응용 프로그램

광도 및 휘도 정의, 해당 방사선량 복사 강도 및 광도 정의
구면 삼각형의 구면 $초과$ E 계산
BEM(Boundary Element Method)을 이용한 전위 계산
금속 착화체 내 리간드의 크기를 평가하려면 리간드 콘 각도를 참조한다.
전하 분포 주변의 전계 및 자기장 강도 계산
가우스의 법칙 도출
열전달 시 방사전력 계산 및 조사
Rutherford 산란에서의 단면 계산
라만 산란에서의 단면 계산
광섬유 수용 콘의 입체 각도

공통 객체에 대한 입체 각도

원뿔, 구형 캡, 반구

구체 내의 원뿔(1)과 구형 캡(2)의 단면.이 그림에서

θ

=

A/

2

및

r

=

1

입니다.

원뿔의 정점이 솔리드 앵글의 정점에 있고 정점이 2µ인 솔리드 앵글은 단위 구면에서 구형 캡의 영역이다.

\displaystyle \Omega = 2\pi \left(1-\cos \theta \오른쪽)\=4\pi \sin ^{2}{\frac {\theta }{2}.}

cos $θ1 -$ // $2$ 와² $같이 작은$ $such$ 의 경우, 이것은 원의 면적인 ,로² 감소한다.

위는 구면 좌표의 단위 표면 요소를 사용하여 다음과 같은 이중 적분을 계산하면 알 수 있습니다.

{displaystyle} {0} {2\pi } {\int _{0} {{2\pi } d\int \theta ',d\theta ',d\phi &=\int _{0} {0} {\theta } {\int \int \ta =\end { aligned}

이 공식은 미적분을 사용하지 않고도 도출될 수 있다.2200년 이상 전에 아르키메데스는 구형의 모자의 표면적이 구형의 모자의 테두리로부터 모자의 대칭축이 ^[1]모자와 교차하는 지점까지의 거리와 같은 원의 면적과 항상 같다는 것을 증명했다.다이어그램에서 이 반지름은 다음과 같이 표시됩니다.

(Displaystyle 2r sin)}

따라서 단위 구체의 경우 구면 캡의 입체 각도는 다음과 같이 주어진다.

\displaystyle \Omega = 4\pi \sin ^{2}{\frac {theta }{2}=2\pi \left(1-\cos \theta \오른쪽).}

$θ$ = $θ$ /2일 때 구면 캡은 입체각 2θ의 반구가 된다.

원뿔의 보완체의 입체 각도는 다음과 같다.

4\pi -\Omega = 2\pi \left(1+\cos \theta \right)= 4\pi \cos ^{2}{\frac {\theta }{2}}.

이것은 또한 위도 $θ$ 에 위치한 천문 관측자가 지구가 회전할 때 볼 수 있는 천구 부분의 단단한 각도이다.적도에서 모든 천구를 볼 수 있고, 어느 극에서나 절반만 볼 수 있다.

원뿔의 축에서 $θ$ 의 각도로 절단되어 원뿔의 정점을 통과하는 구면 캡의 세그먼트에 의해 분할된 솔리드 각도는 다음 공식으로^[2] 계산할 수 있다.

(\displaystyle \Omega = 2\left[\arccos \sin \theta }{\sin \theta }}\right)-\cos \theta \leftcos \frac \frac \tan \theta }\right)}

예를 들어, $θ$ = $-disp이면$ 위의 구면 캡 공식으로 환원됩니다. 첫 번째 항은 $θ$ 가 되고 두 번째 $항$ 은 cos $θ$ 가 됩니다.

사면체

OABC를 삼각면 ABC에 의해 서브텐딩된 O에서 원점을 갖는 사면체의 정점으로 하자. ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ 서 a ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ , ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ , ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ $→$ { $displaystyle$ { $vec$ { $a$ } \ , { \ $vec$ { $b$ } \ , { \ vec { $c$ } } } 、 { \ , { \ $vec$ { c } } } } } 、 { \ , { \ , { \ , { \ } } } 、 { \ } } } 、 { \ vec { \ vec { \ } } } } } a ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ 정점 각도 $θ$ 를_a 각도 BOC로 정의하고 그에 따라 $θ b$ , $θ$ 를_c 정의한다. $\phi _{ab}$ {\ $displaystyle \phi$ _ ${ab}$ 를 $\phi _{ab}$ 사면체면 OAC와 OBC를 포함하는 평면 사이의 이면각으로 하고, $\phi _{bc}$ $\phi _{ac}$ {\ $displaystyle \phi$ _ ${ac$ b $\phi _{bc}$ {\ $displaystyle \phi$ _ ${bc}}$ 를 $\phi _{bc}$ 각각 정의한다.삼각형 표면 ABC에 의해 기울어진 입체각 $δ$ 는 다음과 같이 주어진다.

\displaystyle \Omega =\left(\phi _{ab}+\phi _{bc}+\phi _{ac}\right)\\pi .}

이는 구면초과이론에서 비롯되며, 이는 다음과 같이 사면체의 4개의 내부고체각의 합에 대해 "평면삼각형의 내부각의 합은 $θ$ 와 같다"는 정리와 유사한 정리가 있다는 사실로 이어진다.

\displaystyle \sum _{i=1}^4}\Omega _{i}=2\sum _{i=1}^6}\phi _{i}\-4\pi ,}

여기서 $\phi _{i}$ i $\$ _ ${i}$ 는 $\phi _{i}$ 사면체 면 OAB, OAC, OBC 및 ^[3]ABC를 포함하는 두 평면 사이의 6개의 이면각 모두에 걸쳐 있습니다.

순수하게 정점 각도 $θ a$ , $θ$ 의_b_c 함수인 원점 O에서 사면체의 고체 각도를 계산하는 유용한 공식은 L'Huilier의 정리에^[4]^[5] 의해 다음과 같이 주어진다.

({displaystyle \tan \leftfrac {1}{4}\Omega \right}={{s}{right}\tan \leftfrac {ta _{s}-\tan \leftfrac _{s}-{ta}-{b}\tan \tan \fracta_{ta})_{ta}_ta}{ta}_ta}_{ta}\ta}_ta}_ta}_ta}\ta}_ta}\ta_ta_ta}

어디에

(\displaystyle \theta _{s}=secfrac {theta _{a}+\theta _{b}+{c}}{2}).}

또 다른 흥미로운 공식은 정점을 3차원 공간에서 벡터로 표현하는 것이다.a ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ , ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ , ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ $→$ {\ $displaystyle {a}$ \ , , ${\vec$ {b $}$ \ , ${\vec {$ c}}}을 ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ 정점 A, B 및 C의 벡터 위치라고 하고 $a$ , b $및$ c를 각 벡터(원점 거리)의 크기라고 $합니다$ .삼각형 표면 ABC에 의해 서브텐딩되는 고체 각도 $δ$ 는 다음과 같다.^[6]^[7]

(\displaystyle \tan \frac {1} {2}} \ Omega \ right } = frac { left frac { a } \ \ vec { b } \ right } { cdot { c + \ left vec { a } } \ cdvec { c } \ cdve { c } } {\ 。

어디에

(\displaystyle\left\vec {a}\right = cdot(\vec {b}\times\vec {c}})

는 3개의 벡터의 스칼라 삼중곱을 ${\vec {a}}\cdot {\vec {b}}$ a ${\vec {a}}\cdot {\vec {b}}$ b $→$ {\ $displaystyle {a}\cdot$ {b $}}$ 는 $스칼라$ 곱을 나타냅니다.

여기서 음의 입체각이나 부정확한 입체각이 발생하지 않도록 주의해야 합니다.잠재적인 오류의 원인 $중$ 하나는 a, $b$ , c가 잘못된 권선을 가지고 $있는$ 경우 스칼라 삼중곱이 음수일 수 있다는 것입니다.방정식의 다른 부분은 권선에 의존하지 않기 때문에 컴퓨팅은 충분한 해결책입니다.다른 함정은 스칼라 삼중곱이 양수이지만 제수는 음수일 때 발생합니다.이 경우 음의 값이 반환되며, 이 $값$ 은 by만큼 증가해야 합니다.

피라미드

정점 $각도$ $a$ 와 b(피라미드의 반대 측면에 대해 측정된 이면체 각도)를 가진 네 변의 오른쪽 직사각형 피라미드의 입체 각도는 다음과 같다.

(\displaystyle \Omega = 4\arcsin \left (\sin \left \left \left a \over 2)\sin \left b \over 2)\right).}

피라미드 기부의 변 길이( $α$ 및 β)와 기초 직사각형의 중심에서 피라미드 꼭대기(구체의 중심)까지의 거리( $d$ )를 모두 알고 있다면, 위의 방정식은 다음과 같이 조작할 수 있다.

\Omega = 4\arctan {frac \alpha \rt {4d^{2}+\alpha ^{2}+\alpha ^{2}}}}}.

피라미드 바닥이 $반지름$ r의 규칙적인 n 변 다각형이고 피라미드 $높이$ h인 오른쪽 n-고날 피라미드의 입체 각도는 다음과 같다.

(\displaystyle \Omega = 2\pi - 2n\arctan \leftfrac \frac \tan \leftpi \over n } \ right { 1 + {r^{2} \over h^{2}} } } \ right ）}

가장자리 { $s 1,$ $s 2},$ ... $s$ 를_n 나타내는 단위 벡터의 시퀀스에 의해 정의된 n면 베이스가 있는 임의의 피라미드의 솔리드 각도는 다음과 ^[2]같이 효율적으로 계산할 수 있습니다.

\Omega = 2\pi - \displays _ {j=1}^{n}\left(\left(s_{j-1}s_{j}\right)\left(s_{j+1}\right)-\left(s_{j-1}s_{j}s_{j}\right)+{j}

여기서 괄호(* *)는 스칼라 곱이고 각 괄호[* *]는 스칼라 삼중곱이며 i는 가상의 단위입니다. $s 0$ = $s n$ $및 1$ s = $s$ 의_{n + 1} 인덱스가 순환됩니다.복잡한 곱은 폴리곤의 각 정점 각도와 연관된 위상을 추가합니다.단, $arg$ 의 브런치컷에서 ${displaystyle$ $\arg$ 2 $\$ $pi}$ 의 $2\pi$ $\arg$ 배수가 손실되어 별도로 추적해야 합니다.또한 거의 평행한 세그먼트의 한계에서 언더플로우를 방지하기 위해 복잡한 단계의 실행 곱이 때때로 확장되어야 합니다.

위도-경도 직사각형

지구상에서 위도-경도 직사각형의 단단한 각도는

\displaystyle \left(\sin \phi _{\mathrm {S} }\right)\left(\theta _{\mathrm {E} }-\theta _{\mathrm {W} },\!\right},\mathrm {srm {sr},\},\sr})

여기서

θ

와_N

θ

는_S 위도의 남북선(라디안의 적도로부터 북쪽으로 각도가 증가하는 위치),

θ

와_E

θ

는_W 경도의 동쪽과 서쪽선(라디안의 각도가 ^[8]동쪽으로 증가하는 위치)이다.수학적으로 이것은 구 주위를

θ E

-

θ W

라디안으로 스윕한 각도

θ N

-

θ

의_S 호를 나타냅니다.경도가 2µ 라디안, 위도가

µ

라디안인 경우 솔리드 각도는 구면 각도입니다.

위도-경도 직사각형은 직사각형 피라미드의 단단한 각도와 혼동해서는 안 된다.직사각형 피라미드의 모든 네 변이 거대한 원호를 그리며 구의 표면을 교차합니다.위도-경도 직사각형의 경우 경도선만 큰 원호이며 위도선은 그렇지 않습니다.

천체

각도 직경의 정의를 사용하여 천체의 입체 각도에 대한 공식은 물체의 ${\textstyle R}$ R $(\textstyle$ R ${\textstyle R}$ 과 관찰자에서 물체까지의 $거리$ d $(\displaystyle$ d $d$ 로 정의할 수 있습니다.

\displaystyle \Omega = 2\pi \left(1-{\frac {d^{2}-R^{2}}{d}}\right): d\geq R.}

태양과 달의 적절한 평균값(지구를 기준으로)을 입력하면 태양의 평균 고체각은 6.794×10⁻⁵ 스테라디안이고 달의 평균 고체각은 6.418×10⁻⁵ 스테라디안이다.전체 천구의 관점에서 태양과 달의 부분 끝 평균 부분 면적은 각각 0.0005406%(5.406ppm)와 0.0005107%(5.107ppm)이다.이러한 입체 각도가 거의 같은 크기이기 때문에, 달은 일식 동안 지구와 달 사이의 거리에 따라 개기 일식과 고리 일식을 둘 다 일으킬 수 있다.

임의의 치수의 입체 각도

d차원 유클리드 공간에서 단위 구체의 $완전한 (d$ - 1)차원 구면에 의해 소분된 고체 각도는 임의의 수의 $d차원$ 으로 정의될 수 있다.구면 대칭을 갖는 계산에서는 종종 이 입체 각도 계수가 필요하다.그것은 식에 의해 주어진다.

({displaystyle \Omega _{d}=black {2\pi ^{\flac {d}{2}}{\Gamma \leftflac {d}{2}}}},

여기서

δ

는 감마 함수이다.d가 정수일

경우

감마 함수를 ^[9]명시적으로 계산할 수 있다.따라서

_{d}=case{\frac {1}{\leftfrac {d}{2}}-1\right!}2\pi^{\frac {d}{2}}\&dfrac {even}\{\frac {1}{2}\left(d-1\right)\right!}{(d-1)!}2^{d}\pi^{\frac {1}{2}}(d-1)}\&d420text{홀수}}.\end {case}

이는 길이 $2µr$ 의 둘레로 둘러싸인 2D 원에 대해 면적 $4µr$ 로² 둘러싸인 3D 구에 대해 4µ 스테라디안의 예상 결과를 제공한다.또한 원점 중심의 1D "구"가 구간 $[- r,$ $r]$ 이고 이것이 두 개의 제한점에 의해 경계가 되는 1D 사례에 대해 약간 덜 분명한 2를 제공합니다.

임의의 차원에서의 벡터 공식에 대한 대응 부분은 Aomoto에 의해 그리고 Ribando에 ^[12]의해 독립적으로 도출되었다.무한 다변량 Taylor 급수로 표현합니다.

\displaystyle \Omega =\Omega _{d}{\frac {왼쪽 \det(V)\right }{(4\pi)^{d/2}}\sum_{\vec {a}\in \mathbbb {n}_{0}_{\binom {d}\left[\frac {d}_2-{j}_i}_sum}_{{j}}}\prod _{i}\Gamma \left({\frac {1+\sum _{m\neq i}a_{im}}{2}}\right) {\vec {a}}}\right} {\vec {\vec {a}}.}

d

단위

{\vec {v}}_{i}

v

{\vec {v}}_{i}

{\

style

{\display

{v}} _

{i

}

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

、

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

{\vec {v}}_{i}

i

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

→

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

=

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

i =

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

i =

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

1 \

\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1

α

style _

_

_ them _ _ {\ {\ {\ {\ {\ = i

{\vec {v}}_{i}

_ _ {\ given given given given given given given given given given given given{\ {\ given given given given given → i {\ {\ given{\ given{\ given{\ given{\ given{\ given{\ given{\ given{\ given given given given given

cdot {v}}_{j}=\alpha

_

{ji},\alpha

_

{ii

}=

1

가변은 나는, 1≤ 나는 < j, j≤ d{\displaystyle \alpha_{ij},1\leq i<, ∈ R({\displaystyle{\vec{\alpha}}=(\alpha_{12},\dotsc ,\alpha_{1d},\alpha_{23},\dotsc ,\alpha_{d-1,d})\in\mathbb{R}^{\b j\leq d}는 많은 제어 입출력 α →)(α 12,…, α 1d, α 23일…,α d− 1, d)을 형성하 α.inom

{d}{2

"일치"

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

a

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

(

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

12

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

,

…,

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

-

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

,

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

d )

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

( N 0 (

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

- 2

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

)

{\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},

{

display

style {a} = (

a

_ {

12

, \

dotsc

, a _ 1

dotsc

, a )

、

_ 1

dot

sc .

e

{\

vec }

{{\

vec {a}}=\vec

\

alpha _{ij}^{a_{

ij

{\textstyle {\vec {\alpha }}^{\vec {a}}=\prod \alpha _{ij}^{a_{ij}}}

\mathbb {N} _{0}

서

\mathbb {N} _{0}

0

\mathbb {N} _{0}

{\

displaystyle

\mathbb {

N}

_

{

0}} =

\mathbb {N} _{0}

0으로 시작하는 음이 아닌 정수 또는 자연수에 주의하십시오.표기법 j나는}{\displaystyle \alpha_{ji}j>;나는{\displaystyle j>, 나는}나는 j 가변 α{\displaystyle \alpha_{ij}}, 나는{\displaystyle a_{ji} j}이 되어 멱지수도 비슷하게. 따라서, 용어에 내가 나는 m{\textstyle \sum_{나는m\neq}a_{루멘}}∑ m≠ 모든 용어에 대한 합을 의미하 α.s에

{\vec {a}}

→

{\

displaystyle

{\

vec

여기서 l은 첫 번째 또는 두 번째 인덱스로 표시됩니다.이 시리즈가 수렴되는 곳에서는 벡터에 의해 정의된 솔리드 각도로 수렴됩니다.

레퍼런스

^ "Archimedes on Spheres and Cylinders". Math Pages. 2015.
^ ^a ^b Mazonka, Oleg (2012). "Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps". arXiv:1205.1396 [math.MG].
^ Hopf, Heinz (1940). "Selected Chapters of Geometry" (PDF). ETH Zurich: 1–2.
^ "L'Huilier's Theorem – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.
^ "Spherical Excess – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.
^ Eriksson, Folke (1990). "On the measure of solid angles". Math. Mag. 63 (3): 184–187. doi:10.2307/2691141. JSTOR 2691141.
^ Van Oosterom, A; Strackee, J (1983). "The Solid Angle of a Plane Triangle". IEEE Trans. Biomed. Eng. BME-30 (2): 125–126. doi:10.1109/TBME.1983.325207. PMID 6832789. S2CID 22669644.
^ "Area of a Latitude-Longitude Rectangle". The Math Forum @ Drexel. 2003.
^ Jackson, FM (1993). "Polytopes in Euclidean n-space". Bulletin of the Institute of Mathematics and Its Applications. 29 (11/12): 172–174.
^ Aomoto, Kazuhiko (1977). "Analytic structure of Schläfli function". Nagoya Math. J. 68: 1–16. doi:10.1017/s0027763000017839.
^ Beck, M.; Robins, S.; Sam, S. V. (2010). "Positivity theorems for solid-angle polynomials". Contributions to Algebra and Geometry. 51 (2): 493–507. arXiv:0906.4031. Bibcode:2009arXiv0906.4031B.
^ Ribando, Jason M. (2006). "Measuring Solid Angles Beyond Dimension Three". Discrete & Computational Geometry. 36 (3): 479–487. doi:10.1007/s00454-006-1253-4.

추가 정보

Jaffey, A. H. (1954). "Solid angle subtended by a circular aperture at point and spread sources: formulas and some tables". Rev. Sci. Instrum. 25 (4): 349–354. Bibcode:1954RScI...25..349J. doi:10.1063/1.1771061.
Masket, A. Victor (1957). "Solid angle contour integrals, series, and tables". Rev. Sci. Instrum. 28 (3): 191. Bibcode:1957RScI...28..191M. doi:10.1063/1.1746479.
Naito, Minoru (1957). "A method of calculating the solid angle subtended by a circular aperture". J. Phys. Soc. Jpn. 12 (10): 1122–1129. Bibcode:1957JPSJ...12.1122N. doi:10.1143/JPSJ.12.1122.
Paxton, F. (1959). "Solid angle calculation for a circular disk". Rev. Sci. Instrum. 30 (4): 254. Bibcode:1959RScI...30..254P. doi:10.1063/1.1716590.
Khadjavi, A. (1968). "Calculation of solid angle subtended by rectangular apertures". J. Opt. Soc. Am. 58 (10): 1417–1418. doi:10.1364/JOSA.58.001417.
Gardner, R. P.; Carnesale, A. (1969). "The solid angle subtended at a point by a circular disk". Nucl. Instrum. Methods. 73 (2): 228–230. Bibcode:1969NucIM..73..228G. doi:10.1016/0029-554X(69)90214-6.
Gardner, R. P.; Verghese, K. (1971). "On the solid angle subtended by a circular disk". Nucl. Instrum. Methods. 93 (1): 163–167. Bibcode:1971NucIM..93..163G. doi:10.1016/0029-554X(71)90155-8.
Gotoh, H.; Yagi, H. (1971). "Solid angle subtended by a rectangular slit". Nucl. Instrum. Methods. 96 (3): 485–486. Bibcode:1971NucIM..96..485G. doi:10.1016/0029-554X(71)90624-0.
Cook, J. (1980). "Solid angle subtended by a two rectangles". Nucl. Instrum. Methods. 178 (2–3): 561–564. Bibcode:1980NucIM.178..561C. doi:10.1016/0029-554X(80)90838-1.
Asvestas, John S..; Englund, David C. (1994). "Computing the solid angle subtended by a planar figure". Opt. Eng. 33 (12): 4055–4059. Bibcode:1994OptEn..33.4055A. doi:10.1117/12.183402. 에라툼 따오기vol 50 (2011) 페이지 059801.
Tryka, Stanislaw (1997). "Angular distribution of the solid angle at a point subtended by a circular disk". Opt. Commun. 137 (4–6): 317–333. Bibcode:1997OptCo.137..317T. doi:10.1016/S0030-4018(96)00789-4.
Prata, M. J. (2004). "Analytical calculation of the solid angle subtended by a circular disc detector at a point cosine source". Nucl. Instrum. Methods Phys. Res. A. 521 (2–3): 576. arXiv:math-ph/0305034. Bibcode:2004NIMPA.521..576P. doi:10.1016/j.nima.2003.10.098.
Timus, D. M.; Prata, M. J.; Kalla, S. L.; Abbas, M. I.; Oner, F.; Galiano, E. (2007). "Some further analytical results on the solid angle subtended at a point by a circular disk using elliptic integrals". Nucl. Instrum. Methods Phys. Res. A. 580: 149–152. Bibcode:2007NIMPA.580..149T. doi:10.1016/j.nima.2007.05.055.

외부 링크

HCR의 폴리곤 이론(솔리드 앵글은 임의의 폴리곤에 의해 부분화되어 있음)은 Academia.edu에서 구할 수 있습니다.
아서 P.1969년 에든버러, 갈 앤 잉글리스, 스타 아틀라스 노튼.
M. G. Kendall, Griffin's Statistical Monographics & Cours, 편집자: N차원 기하학 강좌, 8번M. G. 켄달, 찰스 그리핀 주식회사Ltd, London, 1961년
Weisstein, Eric W. "Solid Angle". MathWorld.

[1] "Archimedes on Spheres and Cylinders". Math Pages. 2015.

[Mazonka-2] Mazonka, Oleg (2012). "Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps". arXiv:1205.1396 [math.MG].

[3] Hopf, Heinz (1940). "Selected Chapters of Geometry" (PDF). ETH Zurich: 1–2.

[4] "L'Huilier's Theorem – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.

[5] "Spherical Excess – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.

[6] Eriksson, Folke (1990). "On the measure of solid angles". Math. Mag. 63 (3): 184–187. doi:10.2307/2691141. JSTOR 2691141.

[7] Van Oosterom, A; Strackee, J (1983). "The Solid Angle of a Plane Triangle". IEEE Trans. Biomed. Eng. BME-30 (2): 125–126. doi:10.1109/TBME.1983.325207. PMID 6832789. S2CID 22669644.

[8] "Area of a Latitude-Longitude Rectangle". The Math Forum @ Drexel. 2003.

[9] Jackson, FM (1993). "Polytopes in Euclidean n-space". Bulletin of the Institute of Mathematics and Its Applications. 29 (11/12): 172–174.

[10] Aomoto, Kazuhiko (1977). "Analytic structure of Schläfli function". Nagoya Math. J. 68: 1–16. doi:10.1017/s0027763000017839.

[11] Beck, M.; Robins, S.; Sam, S. V. (2010). "Positivity theorems for solid-angle polynomials". Contributions to Algebra and Geometry. 51 (2): 493–507. arXiv:0906.4031. Bibcode:2009arXiv0906.4031B.

[12] Ribando, Jason M. (2006). "Measuring Solid Angles Beyond Dimension Three". Discrete & Computational Geometry. 36 (3): 479–487. doi:10.1007/s00454-006-1253-4.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[12]

Search

입체각

네임스페이스

더

목차