잘린 사면체
Truncated tetrahedron| 잘린 사면체 | |
|---|---|
 (회전 모델을 보려면 여기를 클릭) | |
| 유형 | 아르키메데스의 입체 균일한 다면체 |
| 요소들 | F = 8, E = 18, V = 12 (표준 = 2) |
| 측면 나란히 | 4{3}+4{6} |
| 콘웨이 표기법 | tT |
| 슐레플리 기호 | t{3,3} = h2{4,3} |
| t0,1{3,3} | |
| 위토프 기호 | 2 3 3 |
| 콕서터 다이어그램 | |
| 대칭군 | Td, A3, [3,3], (*332), 순서 24 |
| 로테이션 그룹 | T, [3,3],+ (332), 순서 12 |
| 이면각 | 3-6: 109°28′16″ 6-6: 70°31′44″ |
| 레퍼런스 | U02, C16, W6 |
| 특성. | 반규칙 볼록 |
 유색인종 |  3.6.6 (버텍스 그림) |
 삼면체 (입체 다면체) |  그물 |
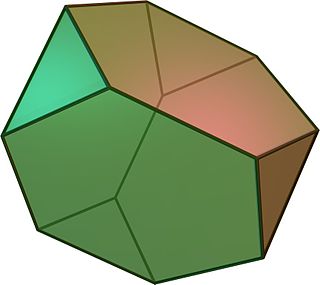
기하학에서 잘린 사면체는 아르키메데스의 고체이다.정육각형 면 4개, 정삼각형 면 4개, 정점 12개, 모서리 18개(2종류)를 가지고 있다.원래 모서리 길이의 1/3에서 정사면체의 4개 정점을 모두 잘라내서 구성할 수 있습니다.
각 정점에서 원래 가장자리 길이의 절반인 사면체를 제거하는 더 깊은 절단을 정류라고 합니다.사면체의 정류는 팔면체를 [1]만든다.
잘린 사면체는 삼각형과 육각형 면을III 포함하는 골드버그 다면체 G(1,1)이다.
잘린 사면체는 콕서터 다이어그램과 함께 칸텔화된 입방체(롬비큐브팔면체)의 정점의 절반을 가진 칸트 입방체라고 할 수 있다.이 구조에는 두 개의 이중 위치가 있으며, 그것들을 결합하면 두 개의 잘린 사면체의 균일한 화합물이 생성된다.
면적 및 볼륨
모서리 길이 a의 잘린 사면체의 면적 A와 부피 V는 다음과 같다.
고밀도 패킹
아르키메데스의 잘린 사면체의 가장 밀도 높은 패킹은 δ =인 것으로 여겨진다.몬테카를로 방법을 사용하여 두 개의 독립 그룹이 [2][3]보고한 대로 207/208.비록 이것이 잘린 사면체에 가장 적합한 패킹이라는 수학적 증거는 없지만, 발견의 통일성과 독립성에 대한 높은 근접성으로 인해 더 밀도가 높은 패킹을 찾을 수 없을 것이다.사실, 모서리의 자른 부분이 아르키메데스의 잘린 사면체보다 약간 작다면,[2] 이 새로운 모양은 공간을 완전히 채우기 위해 사용될 수 있다.
데카르트 좌표
모서리 길이가 θ8인 잘린 사면체의 12개 정점에 대한 데카르트 좌표는 모두 (±1,±1,±3)의 순열이며, 짝수 부호는 다음과 같다.
- (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
- (−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
- (−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
- (+3,−1,−1), (+1,−3,−1), (+1,−1,−3)
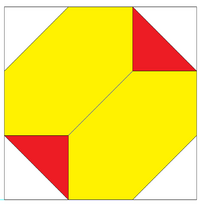 |  |  |
| 경계 상자 내부의 데카르트 좌표를 나타내는 직교 투영: (±3,±3,±3) | 잘린 사면체의 육각형 면은 6개의 동일 평면 정삼각형으로 나눌 수 있다.4개의 새로운 정점에는 데카르트 좌표가 있습니다. (−1,−1,−1), (−1,+1,+1), (+1,−1,+1), (+1,+1,−1).이는 입체적으로 4개의 빨간색 8면체와 6개의 노란색 4면체를 만드는 3D 절개를 나타낼 수 있습니다. | 홀수 수의 마이너스 부호가 있는 정점 순열 세트(±1,±1,±3)는 상호보완적인 잘린 사면체를 형성하고, 그것들을 조합하여 균일한 복합 다면체를 형성한다. |
또 다른 간단한 구조는 잘린 16 셀의 셀로서 4공간 내에 존재하며, 정점은 다음의 좌표 순열로서 존재한다.
- (0,0,1,2)
직교 투영
| 중심 | 엣지 법선 | 페이스 노멀 | 엣지 | 얼굴 |
|---|---|---|---|---|
| 와이어프레임 |  |  |   | |
| 와이어프레임 |  |  |  |  |
| 듀얼 |  |  |  |  |
| 투사적 대칭 | [1] | [1] | [4] | [3] |
구면 타일링
잘린 사면체는 구면 타일링으로도 표현될 수 있으며 입체 투영을 통해 평면에 투영될 수 있습니다.이 투영법은 적합하며 각도는 보존되지만 면적이나 길이는 보존되지 않습니다.구면의 직선은 평면에 원형 호로 투영됩니다.
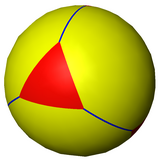 |  삼각형의 |  육각형 중심의 | |
| 맞춤법 투영법 | 입체 투영 | ||
|---|---|---|---|
프리아우프 다면체
잘린 사면체(차수 8D2d 대칭을 가진 잘린 사각형 디셰노이드)의 낮은 대칭 버전은 복잡한 금속 합금과 같은 결정에서 프리아우프 다면체라고 불립니다.이 형태는 축을 중심으로 5개의 다면체에 적합하며,[4] 6-6개의 모서리 부분 집합에 72도의 이면각을 제공합니다.그것은 J. B.의 이름을 따서 지어졌다. Friauf와 그의 1927년 논문 "금속간 화합물2 MgCu의 결정 구조".[5]
사용하다
거대한 잘린 사각형은 엑스포 67에서 "탐험가 남자"와 "제작자 남자" 주제 전시관에 사용되었다.그것들은 기하학적 격자에 볼트로 고정시킨 거대한 강철 거더로 만들어졌다.잘린 사면체는 격자 철골 플랫폼과 상호 연결되었다.이 건물들은 수년 동안 몬트리올의 악천후를 견디기 위해 지어지지 않았기 때문에 엑스포 67이 끝난 후에 모두 철거되었다.그들의 유일한 유물은 몬트리올 시 문서보관소, 캐나다 공공문서보관소, 그리고 [6]당시 관광객들의 사진 소장품이다.
테트라민스 퍼즐은 잘린 사면체 모양을 가지고 있다.이 퍼즐은 잘린 사면체를 4개의 팔면체와 6개의 사면체로 분할하는 것을 보여준다.여기에는 4개의 중심 회전 평면이 포함되어 있습니다.
잘린 사면체 그래프
| 잘린 사면체 그래프 | |
|---|---|
 삼배 대칭 | |
| 꼭지점 | 12개[7] |
| 가장자리 | 18 |
| 반지름 | 3 |
| 직경 | 3개[7] |
| 둘레 | 3개[7] |
| 자기동형 | 24(S4)[7] |
| 색수 | 3개[7] |
| 색채 지수 | 3개[7] |
| 특성. | 해밀턴, 정규, 3-vertex 연결, 평면 그래프 |
| 그래프 및 매개 변수 표 | |
그래프 이론의 수학 분야에서, 잘린 사면체 그래프는 아르키메데스의 고체 중 하나인 잘린 사면체의 꼭지점과 모서리의 그래프인 아르키메데스의 그래프입니다.12개의 꼭지점과 18개의 [8]모서리가 있습니다.연결된 입방 [9]그래프와 연결된 입방 추이 [10]그래프입니다.
| 원형 | 맞춤법 투영법 | |
|---|---|---|
 |  4배 대칭 |  삼배 대칭 |
관련 다면체 및 타일링
| 균일한 사면체 다면체군 | |||||||
|---|---|---|---|---|---|---|---|
| 대칭: [3,3], (*332) | [3,3]+, (332) | ||||||
 |  |  |  | ||||
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| 이중에서 균일한 다면체 | |||||||
 |  |  |  | ||||
| V3.3.3 | V3.6.6 | V3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3 |
또한 정점 구성이 3.6.n.6인 칸틱 다면체와 타일링 시퀀스의 일부입니다.이 와이토프 구조에서 육각형 사이의 가장자리는 퇴화 다이곤을 나타냅니다.
 | 오르비폴드 *n32 | 구면 | 유클리드 | 쌍곡선 | 파라콤팩트 | ||
|---|---|---|---|---|---|---|---|
| *332 | *333 | *433 | *533 | *633... | *∞33 | ||
| 칸트 도형 |  |  |  |  |  |  | |
| 꼭지점 | 3.6.2.6 | 3.6.3.6 | 3.6.4.6 | 3.6.5.6 | 3.6.6 | 3.6.199.6 | |
대칭 돌연변이
이 다면체는 정점 구성(3.2n.2n)과 [n,3] 콕서터 군 대칭을 가진 균일한 잘린 다면체 순서의 일부로 위상적으로 관련된다.
| *n32 잘린 구면 타일링 대칭 돌연변이: t{n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭 *n32 [n,3] | 구면 | 유클리드 | 콤팩트 쌍곡선 | 파라코 | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | ||||
| 잘렸다 수치 |  |  |  |  |  |  |  | ||||
| 기호. | t{2,3} | t{3,3} | t{4,3} | t{5,3} | t{6,3} | t{7,3} | t{8,3} | t{buffic,3} | |||
| 트리아키스 수치 |  |  |  |  |  |  |  | ||||
| 설정. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3 . v∞ ★ | |||
예
잘린 사면체(Matemateca IME-USP)
「 」를 참조해 주세요.
- 4분의 1 입방체 벌집 – 잘린 사면체와 작은 사면체를 사용하여 공간을 채웁니다.
- 잘린 5셀 – 4차원에서도 동일한 균일한 폴리토프
- 잘린 삼면체
- 트리아키스 절단 사면체
- 팔면체 – 정류된 사면체
레퍼런스
- ^ Chisholm, Matt; Avnet, Jeremy (1997). "Truncated Trickery: Truncatering". theory.org. Retrieved 2013-09-02.
- ^ a b Damasceno, Pablo F.; Engel, Michael; Glotzer, Sharon C. (2012). "Crystalline Assemblies and Densest Packings of a Family of Truncated Tetrahedra and the Role of Directional Entropic Forces". ACS Nano. 6 (2012): 609–614. arXiv:1109.1323. doi:10.1021/nn204012y. PMID 22098586. S2CID 12785227.
- ^ Jiao, Yang; Torquato, Sal (Sep 2011). "A Packing of Truncated Tetrahedra that Nearly Fills All of Space". arXiv:1107.2300 [cond-mat.soft].
- ^ http://met.iisc.ernet.in/ ~ lord / webfiles / polyclusters . pdf[베어 URL PDF]
- ^ Friauf, J. B. (1927). "The crystal structure of the intermetallic compound MgCu2". J. Am. Chem. Soc. 49: 3107–3114. doi:10.1021/ja01411a017.
- ^ "Expo 67 - Man the Producer - page 1".
- ^ a b c d e f 그래프 지도책, 페이지=개요, C105
- ^ 그래프 지도책, 267페이지, 잘린 사면체 그래프
- ^ 그래프 지도책, 130페이지, 연결된 입방 그래프, 12개의 꼭지점, C105
- ^ 그래프 지도책, 161페이지, 연결된 입방체 전이 그래프, 12개의 꼭지점, Ct11
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3절부터 제9절까지)
- Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press
| Wikimedia Commons는 잘린 사면체와 관련된 미디어가 있습니다. |


















































