삼면체

삼면체
(모델을 회전하려면 여기를 클릭하십시오.)
유형	카탈루냐 고체
콕시터 다이어그램
콘웨이 표기법	kO
얼굴형	V3.8.8 이등변 삼각형
얼굴	24
가장자리	36
정점	14
유형별 정점	8{3}+6{8}
대칭군	Oh, B3, [4,3], (*432)
회전군	O, [4,3]+, (432)
디헤드각	147°21′00″ 아크코사스3 + 8√2/17)
특성.	볼록한, 얼굴-변형
잘린 큐브 (이중 다면체)	그물

기하학에서 트라이아키스 옥타헤드론(or triangonal triisoctahedron^[1] 또는 kisoctahedron^[2])은 아르키메데스성 이중 고형, 또는 카탈로니아 고형이다. 그것의 이중은 잘린 정육면체다.

그것은 각 면에 삼각형의 피라미드가 추가된 팔면체로 볼 수 있다; 즉 팔면체의 클라이토프다. 그것은 때때로 삼색면체라고도 불리며, 더 완전히는 삼색면체라고도 불린다. 두 이름 모두 팔면체의 각 면마다 세 개의 삼각형 면을 가지고 있음을 반영한다. 사방형 삼면체(三面體)는 팔면체(八面體)의 한 면에 대해 세 개의 정면을 가진 다른 다면체(多面)인 델타(delto) 이코시테트라헤드론의 다른 이름이다.

이 볼록한 다면체는 위상학적으로 오목한 스티로 된 팔면체와 비슷하다. 그들은 얼굴 연결은 동일하지만 정점은 중심에서 다른 상대적 거리에 있다.

짧은 가장자리의 길이가 1인 경우 표면적 및 부피는 다음과 같다.

${\displaystyle {\reasoned}A&=3{\sqrt{7+4{\sqrt{2}}\\\V&={\frac {3+2}{\sqrt{2}}:{2}}:\}\end{aigned}}}}$

데카르트 좌표, 평행 좌표.

Put ${\displaystyle \alpha ={\sqrt {2}}-1}$, then the 14 points ${\displaystyle (\pm \alpha ,\pm \alpha ,\pm \alpha )}$ and ${\displaystyle (\pm 1,0,0)}$, ${\displaystyle (0,\pm 1,0)}$ and ${\displaystyle (0,0,\pm 1)}$ are the vertices of 기원을 중심으로 한 삼면체

긴 가장자리의 길이는 $2{\displaystyle \sqrt{\mathrm{}}}$ ${\$$2$}$$및 짧은 가장자리 $2{\displaystyle \mathrm{}}$- ${\displaystyle 2}$ ${\displaystyle$ 2${\sqrt{$2}}-2$}$와 같다$.$

얼굴은 한 개의 둔각과 두 개의 급성 각도를 가진 이등변 삼각형이다. The obtuse angle equals ${\displaystyle \arccos({\frac {1}{4}}-{\frac {1}{2}}{\sqrt {2}})\approx 117.200\,570\,380\,16^{\circ }}$ and the acute ones equal ${\displaystyle \arccos({\frac {1}{2}}+{\frac {1}{$$4.}{\sqrt{2}})\약 31.399\,714\,809\,92$

직교 투영

3각형 8각형(triakis oxaheadron)은 3개의 대칭 위치를 가지며, 2개는 꼭지점에 위치하며, 1개는 중간 모서리에 위치한다.

직교 투영

투영적 대칭	[2]	[4]	[6]
트리아키스 팔면체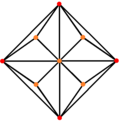
잘림 정육면체

문화참고

• 삼면체(三面體)는 컬트 작가 휴 쿡의 소설 위시스톤과 원더 일꾼의 줄거리에서 중요한 요소다.

관련 다면체

삼면체(三面體)는 정육면체 및 정육면체와 관련된 균일한 다면체(多面體)에 속하는 이중체 중 하나이다.

균일한 팔면체 다면체
대칭: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= 또는	= 또는	=
이중에서 균일한 폴리헤드라까지
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

삼면체(三面體)는 다면체(多面體)와 기울기의 일부로서 쌍곡면으로 확장된다. 이러한 얼굴-변환 수치는 반사 대칭(*n32)을 가진다.

*n32 잘린 틸팅의 대칭 돌연변이: t{n,3} v t
대칭 *n32 [n,3]	구면				유클리드	콤팩트 하이퍼브.		파라코.	비대칭 쌍곡선
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
잘림 수치
기호	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{{{propert,3}	t{12i,3}	t{9i,3}	t{6i,3}
트리아키스 수치
구성.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.1987.1987

삼면체 또한 다면체 및 기울기의 일부로서 쌍곡면으로 확장된다. 이러한 얼굴-변환 수치는 반사 대칭(*n42)을 가진다.

*n42 잘린 틸팅의 대칭 돌연변이: n.8.8 v t
대칭 *n42 [n,4]	구면		유클리드 주	콤팩트 쌍곡선				파라콤팩트
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
잘림 수치
구성.	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
n-11 수치
구성.	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

참조

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3-9)절)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (13반경 볼록 다면체 및 이중체, 17페이지, 삼면체)
• 2008년 사물의 대칭, 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, ISBN 978-1-56881-220-5[1] (21장, 아르키메데스 및 카탈란 다면체의 명명 및 기울기, 284페이지, 트리아키스 옥타헤드론)

외부 링크

• Eric W. Weisstein, Triakis octahedron (Catalan solid) at MathWorld.
• Triakis 팔면체 – 대화형 다면체 모델
• Virtual Reality Polyedra www.georgehart.com: 폴리헤드라 백과사전
  • VRML 본을 뜨다
  • 폴리헤드라 시도를 위한 콘웨이 표기법: "dtC"