잘린 이코시다데카헤드론
Truncated icosidodecahedron| 잘린 이코시다데카헤드론 | |
|---|---|
 (모델을 회전하려면 여기를 클릭하십시오.) | |
| 유형 | 아르키메데스 고체 균일다면체 |
| 요소들 | F = 62, E = 180, V = 120(평균 = 2) |
| 옆얼굴 | 30{4}+20{6}+12{10} |
| 콘웨이 표기법 | bD 또는 taD |
| 슐레플리 기호 | tr{5,3} 또는 { 5 |
| t0,1,2{5,3} | |
| 와이토프 기호 | 2 3 5 |
| 콕시터 다이어그램 | |
| 대칭군 | Ih, H3, [5,3], (*532), 주문 120 |
| 회전군 | I, [5,3],+ (532), 주문 60 |
| 디헤드각 | 6-10: 142.62° 4-10: 148.28° 4-6: 159.095° |
| 참조 | U28, C31, W16 |
| 특성. | 반미레겔볼록조노헤드론 |
 채색면 |  4.6.10 (Vertex 그림) |
 디디아키스 삼권면체 (이중 다면체) | 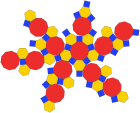 그물 |
기하학에서 잘린 이코시다데카헤드론은 아르키메데스 고체로, 둘 이상의 정규 다각형 면에 의해 구성된 13개의 볼록 이등분 고형물 중 하나이다.
면은 정사각형 30개, 정육각형 20개, 정각형 12개 등 62개다. 그것은 모든 플라토닉과 아르키메데스 고형물 중 가장 많은 가장자리에 정점을 가지고 있지만, 스너브 도데카헤드론은 더 많은 얼굴을 가지고 있다. Of all vertex-transitive polyhedra, it occupies the largest percentage (89.80%) of the volume of a sphere in which it is inscribed, very narrowly beating the snub dodecahedron (89.63%) and Small Rhombicosidodecahedron (89.23%), and less narrowly beating the Truncated Icosahedron (86.74%); it also has by far the greatest volume (206.8 cubic units) 가장자리 길이가 1일 때 프리즘이나 반격자가 아닌 모든 정점 전이성 다면체 중에서 각 정점에서 각도의 합이 가장 크다(90 + 120 + 144 = 354도). 60면 이상의 프리즘이나 반격만이 합이 더 클 것이다. 각각의 얼굴에는 점 대칭(동등, 180° 회전 대칭)이 있으므로 잘린 이코시다데카헤드론은 조노헤드론이다.
이름
| 원래 요하네스 케플러(Johanes Kepler)가 붙인 잘린 이코시다데카헤드론(icosidodechadron)이라는 이름은 오해의 소지가 있다. 이코시다데카헤드론의 실제 잘림에는 사각형 대신 직사각형이 있다. 이 통일되지 않은 다면체는 지형학적으로 아르키메데스 고체와 동일하다. 대체 가능한 이름은 다음과 같다.
|
그레이트 롬비코시도데카헤드론(great rombicosidodechadron)이라는 이름은 (작은) 롬비코시도데카헤드론(compare section Dissection)과의 관계를 가리킨다.
비슷한 이름을 가진 비콘벡스 제복 다면체, 비콘벡스 대 롬비코디도데카헤드론이 있다.
면적 및 부피
가장자리 길이 a의 잘린 이코사이드론의 표면적 A와 볼륨 V는 다음과 같다.[citation needed]
13개의 아르키메데스 고형분 집합이 모든 가장자리 길이가 동일한 상태로 구성되었다면 잘린 이코시도데카헤드론이 가장 클 것이다.
데카르트 좌표, 평행 좌표.
가장자리 길이 2인치 - 2인 잘린 이코시다데카헤드론의 정점에 대한 데카르트 좌표는 모두 원점에 중심을 두고 다음과 같은 고른 순열이다.[4]
- (±1/φ, ±1/φ, ±(3 + φ)),
- (±2/φ, ±φ, ±(1 + 2φ)),
- (±1/φ, ±φ2, ±(−1 + 3φ)),
- (±(2φ - 1, ±2, ±(2 + φ)) 및
- (±φ, ±3, ±2φ),
여기서 φ = 1 + √5/2는 황금 비율이다.
해부
잘린 이코시도데카헤드론은 30제곱미터 위에 큐보이드가 있는 롬비코시도데카헤드론의 볼록한 선체로 높이 대 염기비율은 is이다. 나머지 공간은 내측 펜타곤과 외측 디카곤 사이에 12개, 내측 삼각형과 외측 육각형 사이에 20개 등 균일하지 않은 큐폴라로 해부할 수 있다.
다른 해부는 또한 Rhombicosidodechedral core를 가지고 있다. 안쪽 펜타곤과 바깥쪽 디카곤 사이에 12개의 오각형 로튼대를 가지고 있다. 남은 부분은 토로이드 다면체다.
| 영상을 해부하다 |
|---|
| 이 이미지들은 롬비코시도데카헤드론(보라색)과 잘린 이코시도데카헤드론(녹색)을 보여준다. 가장자리 길이가 1이면 해당 사각형 사이의 거리는 φ이다. |
직교 투영
잘린 이코시다데카헤드론은 정점을 중심으로 한 7개의 특별한 직교 돌출부가 세 가지 유형의 가장자리에 있으며, 세 가지 유형의 면은 사각형, 육각형, 십각형이다. 마지막 두 개는 A와2 H Coxeter2 비행기에 해당한다.
| 중심: | 꼭지점 | 가장자리 4-6 | 가장자리 4-10 | 가장자리 6-10 | 면 정사각형의 | 면 육각형의 | 면 데카곤 |
|---|---|---|---|---|---|---|---|
| 고체 |  |  |  | ||||
| 와이어프레임 | 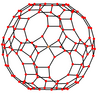 |  | 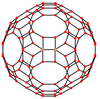 |  |  |  |  |
| 투영적 대칭 | [2]+ | [2] | [2] | [2] | [2] | [6] | [10] |
| 이중 이미지 |  |  |  |  | 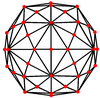 |  | 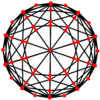 |
구형 틸링 및 슐레겔 도표
잘린 이코시다데카헤드론은 구면 타일링으로도 표현될 수 있으며, 입체 투영을 통해 평면에 투영된다. 이 투영은 각도만 보존하고 면적이나 길이는 보존하지 않는다. 구의 직선은 평면에 원형 호로 투영된다.
| 직교 투영법 | 입체 투영 | ||
|---|---|---|---|
| 데카곤 중심 | 육각 중심 | 정사각형 중심 | |
 |  |  |  |
기하학적 변이
Icosaheadral 대칭 내에는 이등변형을 가진 잘린 이등변형의 기하학적 변형이 무제한 있다. 퇴행 제한 사례로서 잘린 도데면체, 롬비코시다면체, 잘린 이코사면체.
 |  |  |  |  |  |  |  |
잘린 이코시다데카헤드랄 그래프
| 잘린 이코시다데카헤드랄 그래프 | |
|---|---|
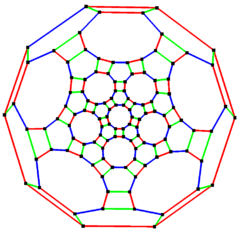 5배 대칭 | |
| 정점 | 120 |
| 가장자리 | 180 |
| 반지름 | 15 |
| 지름 | 15 |
| 둘레 | 4 |
| 자동형성 | 120(A5×2) |
| 색수 | 2 |
| 특성. | 큐빅, 해밀턴, 정규, 제로대칭 |
| 그래프 및 모수 표 | |
그래프 이론의 수학적 분야에서 잘린 이코시다데카헤드 그래프(또는 큰 롬비코사데카헤드 그래프)는 잘린 이코시다데카헤드론의 정점과 가장자리를 나타내는 그래프로, 아르키메데스 고형물 중 하나이다. 정점 120과 가장자리 180을 가지며, 0대칭 및 입방형 아르키메데스 그래프다.[5]
 3중대칭 |  2중대칭 2중대칭 |
및 관면체 틸팅
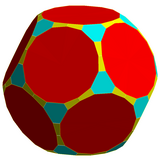 |  |
| 보타이 이코사면체와 도데카면에는 사각형 대신 두 개의 사다리꼴 면이 있다.[6] | |
| 균일한 이두면체 다면체 계열 | |||||||
|---|---|---|---|---|---|---|---|
| 대칭: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | 196{5,3} |
| 이중에서 균일한 폴리헤드라까지 | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | 3V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
이 다면체는 꼭지점 수치(4.6.2p)와 Coxeter-Dynkin 도표를 가진 일련의 균일한 패턴의 구성원으로 간주될 수 있다. p < 6의 경우, 시퀀스의 구성원은 구면 기울기로서 아래에 표시된 전위절제 다면체(조노헤드론)이다. p > 6의 경우 잘린 3헥타르 타일링부터 시작하여 쌍곡면의 기울기이다.
| *n32 전분해 틸팅의 대칭 변이: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] | 유클리드 | 콤팩트 하이퍼브. | 파라코. | 비선선선선 | ||||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i,3] | [9i,3] | [6i,3] | [3i,3] | |
| 치 |  |  |  |  |  |  |  |  |  |  |  | |
| 구성. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| 듀얼스 |  |  |  |  |  |  |  |  |  |  |  |  |
| 구성. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.1987 | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
메모들
- ^ 웬닝어, (모델 16, 페이지 30)
- ^ 윌리엄슨 (3-9, 페이지 94)
- ^ 크롬웰 (82)
- ^ Weisstein, Eric W. "Icosahedral group". MathWorld.
- ^ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
- ^ Symmetrohedra: 일반 폴리곤의 대칭 배치에서 나온 폴리헤드라 Craig S. Kaplan
참고문헌
- Wenninger, Magnus (1974), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, MR 0467493
- Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
- Cromwell, P.; P.; Polyedra, CUP hbk(1997), PB.(1999).
- Eric W. Weisstein, GreatRhombicosidodecahedron (Archimedean solid) at MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra x3x5x - grid".