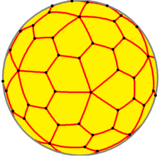
오각형 육면체

오각형 육면체
(회전 모델을 보려면 여기를 클릭)
유형	카탈로니아 솔리드
콕서터 다이어그램
콘웨이 표기법	gD
얼굴형	V3.3.3.5 불규칙 오각형
얼굴	60
가장자리	150
꼭지점	92
유형별 정점	12 {5} 20+60 {3}
대칭군	저는...1/2H₃, [5,3]⁺, (532)
로테이션 그룹	I, [5,3]⁺, (532)
이면각	153°10′43″
특성.	볼록형 안면 전이성 키랄
스누브 12면체 (입체 다면체)	그물

오각형 육면체의 3차원 모형

기하학에서, 오각형 육면체는 카탈로니아의 입체이며, 스누브 12면체의 쌍대이다.서로 거울상(또는 "반동형")인 두 가지 형태가 있습니다.60개의 오각형 면에 걸쳐 있는 92개의 정점이 있습니다.이것은 정점이 가장 많은 카탈로니아 입체이다.카탈로니아와 아르키메데스의 고체들 중에서, 그것은 120개의 꼭지점을 가진 잘린 이십이면체 다음으로 두 번째로 많은 꼭지점을 가지고 있다.

건설

오각형 육면체는 쌍체를 취하지 않고 정육면체로 구성될 수 있다.정십이면체의 12개의 오각형 면에는 오각형 피라미드가 추가되고, 오각형과 모서리를 공유하지 않는 20개의 삼각형 면에는 삼각형 피라미드가 추가된다.피라미드 높이는 12면체의 다른 60개의 삼각형 면과 동일 평면을 이루도록 조정됩니다.그 결과는 오각형 육면체이다.^[1]

기하학.

면은 두 개의 긴 모서리와 세 개의 짧은 모서리를 가진 불규칙한 펜타곤입니다. $\xi \approx 0.943\,151\,259\,24$ $\xi \approx 0.943\,151\,259\,24$ 151 $\xi \approx 0.943\,151\,259\,24$ 24 $\xi \approx 0.943\,151\,259\,24$ {\ $displaystyle$ \xi $\약$ 0. $943,13,259,24}$ 를 $\xi \approx 0.943\,151\,259\,24$ $x^{3}+2x^{2}-\phi ^{2}$ x $x^{3}+2x^{2}-\phi ^{2}$ + $x^{3}+2x^{2}-\phi ^{2}$ $x^{3}+2x^{2}-\phi ^{2}$ - $x^{3}+2x^{2}-\phi ^{2}$ 2 ({ $displaystyle$ x $^3}+2x^2}-\phi$ ^{ $2$ 의 실수 0이라고 하자. 여기서 = $\phi ={\frac {1+{\sqrt {5}}}{2}}$ + $\phi ={\frac {1+{\sqrt {5}}}{2}}$ \ $display$ style \ $phi = frac {1}$ 다음으로 엣지 길이의 $비율$ l\ $displaystyle$ l은 다음과 $l$ 같습니다.

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

+

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

2 -

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

2

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

1

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

74

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

{

displaystyle

l =

scapfrac {1+\xi

}{

2-\xi

^{

2}\약

1.

749,852,566,74

면은 4개의 동일한 둔각과 1개의 예각(두 개의 긴 가장자리 사이)을 가진다.둔각은 $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ θ ( $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ - $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ / $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ ) $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ 118. $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ 62 $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ 45 ( \ $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ $\arccos$ ( - \ $xi / 2$ )\ $45$ 118 $.136,622,$ 758 $,62$ ^{\ $circ$ 이고, 예각은 $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ θ $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ ( - $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 2 $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ / $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 45 2 $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 2 $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 2 + ) $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 45 $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 45 $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 45 9453 45 622 $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ 。이면각은 $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ ( - $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ / ( $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ - $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ ) $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ 153 $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ 45 ${\$ ( \ $displaystyle \arccos$ ( - \ $xi$ / ( $2$ - \ $xi$ ) ) \ $약 153.178,732,558,45^{\circ$ 입니다.스너십면체의 면은 오각형의 꼭지점으로 직접 기능할 수 없습니다.타곤 중심은 그렇지 않습니다.삼각형의 중심과 동일 평면을 이루려면 방사상으로 밀어내야 합니다.결과적으로, 오각형 육면체의 꼭지점들은 모두 같은 구상에 있는 것은 아니며, 정의상 그것은 조면체가 아니다.

한 b{\displaystyle b}로 오각형의 얼굴의 짧은 측면 의미하고, 일정한 t[2]t을 세웠다=44+12ϕ(9+81ϕ − 15)3+44+12ϕ 3− 412≈ 0.471 575년 629622{\displaystyle t={\frac{{\sqrt[{3}]{44(9− 81ϕ − 15) 오각형의 hexecontahedron의 부피와 표면적 찾기 위해서.+12 $\phi (9+{\secrt {81\phi$ -15 $}}}+{\secrt$ [{ $3}}{44+12\phi (9-{\secrt {81\phi -15}}}}-4}}\약$ 0 $.471,575,629,622}}$

다음으로 표면적(A)은 다음과 같습니다.

$A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ 2µ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ + $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ ) $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ 1 - $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ 2 $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ - $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ 2 $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ 162 . $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ $A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ 2 ( \ $displaystyle$ A = $30 b$ ^ { $2$ } \ $cdot ($ 2 + 3 $t$ ) \ $cdot$ \ $cdot {$ 1 - t^ { 2 $}$ } : { 1 - 2 $t^$ 2 、 162 、 162 、 9 . 9 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 . 8 .

볼륨(V)은 다음과 같습니다.

$V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ 3 ( $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ + $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ ) ( $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ - $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ ) $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ ( $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ - $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ t $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ ) $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ 1 $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ - $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ . $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ b $V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ 3 ( \ $display$ V = $scfrac$ { $5b$ ^ { 3 } ( $1$ + $3 t$ ) { 1 - 2 t $}$ \ $cdot$ { 1 - 2 $t$ } $。$

이를 사용하여 이 형상에 대한 구면도 측정을 계산할 수 있습니다.

{\displaystyle \Psi = pi ^{\frac {1}{3}}(6V)^{\frac {2}{3}}{A}}\약 0.98163

바리에이션

모서리 길이가 3개인 오각형 면으로 등면체 변형을 구성할 수 있습니다.

이 변화는 12개의 오각형 면과 20개의 삼각 면의 스너브 십이면체에 피라미드를 추가하여 구성될 수 있으며, 새로운 삼각 면이 다른 삼각형과 동일하고 오각형 면으로 병합될 수 있다.

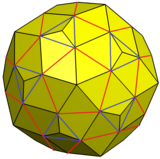보강된 피라미드와 병합된 면이 있는 스누브 12면체	변동 예	그물

직교 투영

오각형 육면체에는 정점에 두 개, 가장자리에 한 개 등 세 개의 대칭 위치가 있습니다.

직교 투영
투사적 대칭	[3]	[5]⁺	[2]
이미지
듀얼 이미지

「」를 참조해 주세요.

레퍼런스

^ 언급
^ "Pentagonal Hexecontahedron - Geometry Calculator". rechneronline.de. Retrieved 2020-05-26.

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3절부터 제9절까지)
Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (13개의 반정형 볼록 다면체 및 그 쌍대(Page 29, 오각형 육면체))
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 [1] (21장, 아르키메데인과 카탈로니아 다면체와 타일링 명명, 287페이지, 5각형 육면체)

외부 링크

Eric W. Weisstein, Pentagonal hexecontahedron (Catalan solid) at MathWorld.
오각형 육면체 – 대화형 다면체 모델

이 다면체 관련 기사는 스텁이다.위키피디아를 확장함으로써 위키피디아를 도울 수 있습니다.

[1] 언급

[2] "Pentagonal Hexecontahedron - Geometry Calculator". rechneronline.de. Retrieved 2020-05-26.

[1]

균일한 20면체 다면체군
대칭 : [5,3], (*532)							[5,3]⁺, (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr {5,3}
이중에서 균일한 다면체

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.5

n32 스너브 타일링 대칭 돌연변이: 3.3.3.n v t
대칭 n32	구면				유클리드	콤팩트 쌍곡선		파라콤프
대칭 n32	232	332	432	532	632	732	832	∞32
스너브 수치
설정.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
자이로 수치
설정.	V3.3.3.2	V3.3.3.3	V3.3.3.4	V3.3.3.5	V3.3.3.6	V3.3.3.7	V3.3.3.8	V3.3.3.★

Search

오각형 육면체

네임스페이스

더

목차

건설

기하학.

바리에이션

직교 투영

관련 다면체 및 타일링

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

오각형 육면체

건설

기하학.

바리에이션

직교 투영

관련 다면체 및 타일링

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.