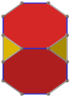
잘린 큐브

잘린 큐브
(모델을 회전하려면 여기를 클릭하십시오.)
유형	아르키메데스 고체 균일다면체
요소들	F = 14, E = 36, V = 24(수평 = 2)
옆얼굴	8{3}+6{8}
콘웨이 표기법	tC
슐레플리 기호	t{4,3}
	t0,1{4,3}
와이토프 기호	2 3 4
콕시터 다이어그램
대칭군	Oh, B3, [4,3], (*432), 주문 48
회전군	O, [4,3],+ (432), 주문 24
디헤드각	3-8: 125°15′51″ 8-8: 90°
참조	U09, C21, W8
특성.	반경형 볼록스
채색면	3.8.8 (Vertex 그림)
삼면체 (이중 다면체)	그물

기하학에서 잘린 입방체 또는 잘린 육면체는 아르키메데스 고체다. 14개의 정면(팔각형 6개, 삼각형 8개), 36개의 가장자리, 24개의 정점을 가지고 있다.

잘린 입방체의 가장자리 길이가 단위인 경우, 이중삼각형 팔면체의 가장자리는 길이 2와 길이 2 + 22이다.

면적 및 부피

가장자리 길이 a의 잘린 큐브 A 영역 및 볼륨 V:

${\displaystyle {\reasoned}A&=2\좌측(6+6{\sqrt{2}}+{\sqrt{3}\우측)^{2}&\ 약 32.434\,6644a^{2}\\V&={\frac {21+14{\sqrt{2}}:{3}a^{3}&\ 약 13.599\,6633a^{3}.\end{정렬}}}$

직교 투영

잘린 정육면체에는 두 가지 유형의 가장자리와 삼각형, 팔각형의 두 가지 면의 중심, 정점 위에 5개의 특별한 직교 돌출부가 있다. 마지막 두 개는 B와₂ A₂ Coxeter 평면에 해당한다.

직교 투영

중심:	꼭지점	가장자리 3-8	가장자리 8-8	면 팔각형	면 삼각형
고체
와이어프레임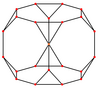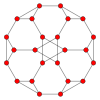
이중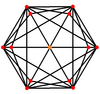
투영적 대칭	[2]	[2]	[2]	[4]	[6]

구면 타일링

잘린 정육면체는 구형 타일링으로도 표현될 수 있으며, 입체 투영을 통해 평면에 투영된다. 이 투영은 각도만 보존하고 면적이나 길이는 보존하지 않는다. 구의 직선은 평면에 원형 호로 투영된다.

	팔각형의	삼각형의
직교 투영법	입체 투영

데카르트 좌표, 평행 좌표.

가장자리 길이가 2㎝인 원점을 중심으로 잘린 육면체의 정점에 대한 데카르트 좌표는 모두 의 순열이다.

(±ξ, ±1, ±1),

여기서 ξ = √2 - 1.

매개변수 ξ은 ±1 사이에서 변경할 수 있다. 값이 1이면 큐브가 생성되고, 0이면 큐보타헤드론이 생성되며, 음의 값은 스스로 교차하는 옥타그램 얼굴을 생성한다.

8진법의 자가 절개된 부분을 제거하여 정사각형을 남기고 삼각형을 육각형으로 자르면 잘린 8진법이 생성되며, 그 시퀀스는 중앙 정사각형이 한 점으로 축소되어 8진법을 만든다.

해부

잘린 정육면체는 중앙 정육면체로 해부할 수 있으며, 정사각형 큐폴레는 각 정사각형의 얼굴 주위에 6개, 모서리에 8개의 정사각형 테트라헤드라가 있다. 이 해부는 정육면체, 사면체, 롬비큐브옥타헤드론 세포가 있는 런치큐빅 큐빅 벌집에서도 볼 수 있다.

이 해부는 두 개의 사각 큐폴레와 중앙 큐브를 제거하여 모든 일반 얼굴을 가진 스튜어트 토로이드를 만드는 데 사용될 수 있다. 이 발굴된 정육면체는 16개의 삼각형, 12개의 사각형, 4개의 옥타곤을 가지고 있다.^[1][2]

정점 배열

그것은 3개의 비콘벡스 균일 다면체와 정점 배열을 공유한다.

잘린 큐브

비콘벡스 대롬비쿠옥타헤드론

대입방옥타헤드론

대록비헥사헤드론

관련 다면체

잘린 입방체는 다른 다면체 및 대칭의 기울기와 관련이 있다.

잘린 정육면체는 정육면체 및 정육면체와 관련된 균일한 다면체군 중 하나이다.

균일한 팔면체 다면체
대칭: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= 또는	= 또는	=
이중에서 균일한 폴리헤드라까지
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

대칭 돌연변이

이 다면체는 꼭지점 구성(3.2n.2n)과 [n,3] Coxeter 그룹 대칭 및 일련의 다면 및 기울기 n.8.8을 갖는 균일한 절단 다면체의 일부로서 위상학적으로 관련이 있다.

*n32 잘린 구형 틸팅의 대칭 돌연변이: t{n,3}
대칭 *n32 [n,3]	구면				유클리드	콤팩트 하이퍼브.		파라코.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
잘림 수치
기호	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{{{propert,3}
트리아키스 수치
구성.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.1987.1987

*n42 잘린 틸팅의 대칭 돌연변이: n.8.8 v t
대칭 *n42 [n,4]	구면		유클리드 주	콤팩트 쌍곡선				파라콤팩트
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
잘림 수치
구성.	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
n-11 수치
구성.	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

교번 절단

입방체의 정점을 교대로 자르면 모따기형 4면체, 즉 4면체의 가장자리 자르기가 된다.

잘린 삼각형 사다리꼴은 입방체 가장자리 잘림으로 형성될 수 있는 또 다른 다면체다.

관련 폴리토페스

잘린 입방체는 잘린 하이퍼큐브 순서에서 두 번째다.

잘린 하이퍼큐브

이미지								...
이름	팔각형	잘린 큐브	잘린 테세락트	잘린 5-큐브	잘린 6-큐브	잘린 7-큐브	잘린 8-큐브
콕시터 다이어그램
정점수	( )v( )	( )v{ }	( )v{3}	( )v{3,3}	( )v{3,3,3}	( )v{3,3,3}	( )v{3,3,3,3}

잘린 칸막이 그래프

잘린 칸막이 그래프
4배 대칭 슐레겔 도표
정점	24
가장자리	36
자동형성	48
색수	3
특성.	큐빅, 해밀턴, 정규, 제로대칭
그래프 및 모수 표

그래프 이론의 수학적 분야에서 잘린 입체 그래프는 잘린 입방체의 정점과 가장자리의 그래프로, 아르키메데스 고형물 중 하나이다. 24개의 정점과 36개의 가장자리를 가지고 있으며, 큐빅 아르키메데스 그래프 입니다.^[3]

직교

참고 항목

• 회전 잘린 큐브
• 잘린 큐브의 골격을 포함하는 그래프 계열인 큐브 연결 주기

참조

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3-9)절)
• Cromwell, P. P. Polyedra, CUP hbk(1997), PBk(1999). 제2장 79-86장 아르키메데스 고형분

외부 링크

• Eric W. Weisstein, Truncated cube (Archimedean solid) at MathWorld.
  • Weisstein, Eric W. "Truncated cubical graph". MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra o3x4x - tic".
• 대화형 3D 보기를 사용하여 잘린 큐브의 편집 가능한 인쇄 가능
• 균일 폴리헤드라
• Virtual Reality Polyedra www.georgehart.com: 폴리헤드라 백과사전
  • VRML 본을 뜨다
  • 폴리헤드라 시도를 위한 콘웨이 표기법: "tC"