스너브 큐브
Snub cube| 스너브 큐브 | |
|---|---|
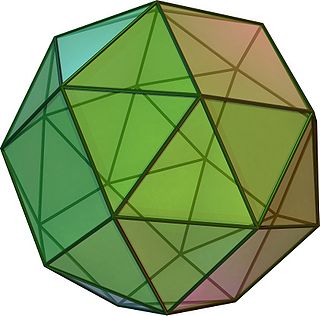 (회전 모델을 보려면 여기를 클릭) | |
| 유형 | 아르키메데스의 입체 균일한 다면체 |
| 요소들 | F = 38, E = 60, V = 24 (표준 = 2) |
| 측면 나란히 | (8+24){3}+6{4} |
| 콘웨이 표기법 | sc |
| 슐레플리 기호 | sr {4,3} s { 3 { s { \ { } \ \ \ { } } |
| ht0,1,2{4,3} | |
| 위토프 기호 | 2 3 4 |
| 콕서터 다이어그램 | |
| 대칭군 | 오,1/2B3, [4,3],+ (432), 주문 24 |
| 로테이션 그룹 | O, [4,3],+ (432), 주문 24 |
| 이면각 | 3-3: 153°14′04″ (153.23°) 3-4: 142°59′00″ (142.98°) |
| 레퍼런스 | U12, C24, W17 |
| 특성. | 반규칙 볼록 키랄 |
 유색인종 |  3.3.3.3.4 (버텍스 그림) |
 오각형 이십면체 (입체 다면체) | 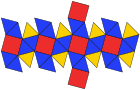 그물 |
기하학에서, 스누브 큐브 또는 스누브 큐브 팔면체는 6개의 정사각형과 32개의 정삼각형 38개의 면을 가진 아르키메데스 입체이다.60개의 모서리와 24개의 정점이 있습니다.
이것은 키랄 다면체이다. 즉, 서로 거울상(또는 "반동형체")인 두 가지 다른 형태를 가지고 있다.두 형태의 결합은 두 개의 꼭지점 집합의 볼록한 껍질은 잘린 정육면체이다.
케플러는 1619년 그의 Harmonices Mundi에서 그것을 큐버스 시무스로 라틴어로 처음 명명했다.H. S. M. 콕서터는 이것이 정육면체와 마찬가지로 정육면체라고 불리며, 수직 확장 슐레플리 { 4 {{style {3\ {Bmatrix를 가지며, 잘린정육면체의 대체를 나타낸다. { t \ \ { } \ \ 3 { }
치수
모서리 길이가 1인 스너브 큐브의 경우 표면적 및 부피는 다음과 같습니다.
여기서 t는 트리보나치 상수입니다.
만약 원래의 스너브 큐브가 모서리 길이 1을 가지고 있다면, 그것의 이중 오각형 이십면체는 변의 길이를 가지고 있다.
- {\{1} 1}} {\text {\ {\1}} {\frac {\frac} {\frac {\frac {t+1}} {\ {\ {\frac} : 약 0
일반적으로 측면 가인 스너브 의 부피는 위의 [1]t를 트리보나치 상수로 사용하여 다음과 같은 공식으로 구할 수 있습니다.
3 - + t + 3 - 7. 3 { V = { a } \ { 3{ t - 1 } + + } { 3 rt { 2 - t } } } } } 、 ( 7889
데카르트 좌표
정육면체의 정점에 대한 데카르트 좌표는 모두 짝수 배열이다.
- (±1, ±1/t, ±t)
짝수 플러스 기호와 홀수 플러스 기호를 가진 모든 홀수 순열(여기서 t ≤ 1.83929는 트리보나치 상수)이 있습니다.짝수 순열을 홀수 플러스 기호로, 짝수 플러스 기호로 홀수 순열을 취하면 거울 이미지라는 다른 스너브 큐브를 얻을 수 있습니다.그것들을 모두 합치면 두 개의 스너브 큐브의 화합물이 만들어집니다.
이 스너브 큐브는 가 2 + - 2 \alpha =인 모서리를 가지고 있으며, 이는 방정식을 만족시키는 숫자이다.
라고 쓸 수 있습니다.
단위 모서리 길이를 가진 스너브 큐브를 얻으려면 위의 모든 좌표를 위에 주어진 값 α로 나눕니다.
직교 투영
스너브 큐브에는 A 및22 B Coxeter 평면에 해당하는 삼각형과 정사각형이라는 두 가지 유형의 면 중앙에 두 개의 특수 직교 투영부가 있습니다.
| 중심 | 얼굴 삼각형 | 얼굴 광장 | 엣지 |
|---|---|---|---|
| 단단한 |  |  |  |
| 와이어프레임 |  |  |  |
| 투사적 대칭 | [3] | [4]+ | [2] |
| 듀얼 |  |  |  |
구면 타일링
스너브 큐브는 구형 타일링으로 표현될 수 있으며 입체 투영을 통해 평면에 투영될 수 있습니다.이 투영법은 적합하며 각도는 보존되지만 면적이나 길이는 보존되지 않습니다.구면상의 대원호(지오데식)는 평면상에 원호로 투영됩니다.
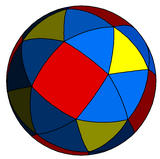 |  정사각형 중심의 |
| 맞춤법 투영법 | 입체 투영 |
|---|
기하 관계
스너브 큐브는 큐브의 6개 면을 바깥쪽으로 당겨 더 이상 접촉하지 않도록 한 다음, 각 면을 중심으로 작은 회전(모두 시계방향 또는 모두 시계반대방향)을 시켜서 생성될 수 있습니다.
스너브 큐브는 또한 교대 과정을 통해 잘린 정육면체에서 파생될 수 있다.잘린 정육면체의 24개의 정점은 정육면체와 위상적으로 동등한 다면체를 형성하고, 나머지 24개는 정육면체의 거울상을 형성합니다.결과 다면체는 정점 추이적이지만 균일하지는 않습니다.
아르키메데스의 균일한 스너브 큐브에 비해 약간 더 작은 정사각형 면과 약간 더 큰 삼각형 면을 가진 "개선된" 스너브 큐브는 구면 [2]디자인으로 유용하다.
관련 다면체 및 타일링
스너브 큐브는 큐브 및 정팔면체와 관련된 균일한 다면체 계열 중 하나입니다.
| 균일한 팔면체 다면체 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 대칭: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} | t{3,4} t{31,1} | {3,4} {31,1} | rr{4,3} s2{3,4} | tr{4,3} | sr{4,3} | h{4,3} {3,3} | h2{4,3} t{3,3} | s{3,4} s{31,1} |
= | = | = | ||||||||
| 이중에서 균일한 다면체 | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
이 반정규 다면체는 정점 도형 (3.3.3.n)과 콕서터-다인킨 도형을 가진 스누브 다면체와 타일링의 수열의 구성원이다.이 그림들과 그 이중들은 n = 6에 대해 유클리드 평면에 있는 (n32) 회전 대칭을 가지고 있고, 더 높은 n에 대해 쌍곡 평면을 가지고 있다.이 급수는 n=2로 시작하며, 한 개의 면 집합이 이각형으로 퇴화된다고 볼 수 있습니다.
| n32 스너브 타일링 대칭 돌연변이: 3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 대칭 n32 | 구면 | 유클리드 | 콤팩트 쌍곡선 | 파라콤프 | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| 스너브 수치 |  |  |  |  |  |  |  |  |
| 설정. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| 자이로 수치 |  |  |  |  |  |  |  |  |
| 설정. | V3.3.3.2 | V3.3.3.3 | V3.3.3.4 | V3.3.3.5 | V3.3.3.6 | V3.3.3.7 | V3.3.3.8 | V3.3.3.★ |
스너브 큐브는 일련의 스너브 다면체와 정점 그림 3.3.4.3.n의 타일링에서 두 번째이다.
| 스너브 타일링의 4n2 대칭 돌연변이: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 대칭 4n2 | 구면 | 유클리드 | 콤팩트 쌍곡선 | 파라콤프 | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| 스너브 수치 |  |  |  |  |  |  |  |  |
| 설정. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| 자이로 수치 |  |  |  |  | ||||
| 설정. | V3.3.4.3.2 | V3.3.4.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.★ |
스누브 입방체 그래프
| 스누브 입방체 그래프 | |
|---|---|
 4배 대칭 | |
| 꼭지점 | 24 |
| 가장자리 | 60 |
| 자기동형 | 24 |
| 특성. | 해밀턴, 정규 |
| 그래프 및 매개 변수 표 | |
그래프 이론의 수학 분야에서, 스누브 입방체 그래프는 아르키메데스의 고체 중 하나인 스누브 입방체의 꼭지점과 모서리의 그래프이다.24개의 꼭지점과 60개의 모서리가 있으며 아르키메데스 [3]그래프입니다.
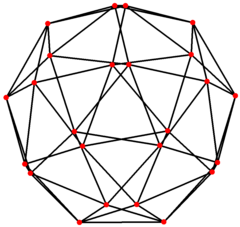 |
「 」를 참조해 주세요.
레퍼런스
- ^ "Snub Cube - Geometry Calculator". rechneronline.de. Retrieved 2020-05-26.
- ^ R.H. 하딘과 N.J.A.의 "구면 설계" 슬론
- ^ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
- Jayatilake, Udaya (March 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette. 89 (514): 76–81. doi:10.1017/S0025557200176818. S2CID 125675814.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3절부터 제9절까지)
- Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
외부 링크
- Eric W. Weisstein, Snub cube (Archimedean solid) at MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra s3s4s - snic".
- 통일된 다면체
- 가상현실 폴리헤드라 폴리헤드라 백과사전
- 대화형 3D 뷰가 있는 Snub Cube의 편집 가능한 네트





![{\displaystyle t={\frac {1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}}{3}}\approx 1.839\,286\,755\,21.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00b5dd3c4eadfd955c9c41e5b960d0f19ac5ca7e)

 스너브
스너브 

![{\displaystyle {\begin{aligned}\alpha &={\sqrt {{\frac {4}{3}}-{\frac {16}{3\beta }}+{\frac {2\beta }{3}}}}\approx 1.609\,72\\\beta &={\sqrt[{3}]{26+6{\sqrt {33}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a8d7d106963ee92fcc2a3159bcccb8de89d6bfb)



















































