질라시 다면체

질라시 다면체
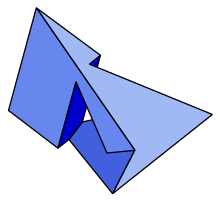유형	토로이드 다면체
얼굴	육각 7개
가장자리	21
정점	14
오일러 차르.	0(제너스 1)
꼭지점 구성	6.6.6
대칭군	C1, [ ]+, (11)
이중 다면체	차사르 다면체
특성.	논콘벡스

실라시 다면체는 비콘벡스 다면체로서, 토러스(torus)로, 7개의 육각면을 가지고 있다.

색상과 대칭

이 다면체의 각 면은 서로 날을 이룬다.그 결과, 7가지 색상 정리에 대한 하한을 제공하여 모든 인접 면에 색상을 입히는데 7가지 색상이 필요하다.그것은 180도 대칭의 축을 가지고 있다; 세 쌍의 얼굴은 일치한다. 세 쌍의 얼굴은 다면체와 같은 회전 대칭을 가진 하나의 손상되지 않은 육각형을 남긴다.실라시 다면체의 14개의 정점과 21개의 가장자리는 히우드 그래프를 토러스 표면에 내장한다.^[1]

면 인접성 완성

사면체와 질라시 다면체는 각각의 얼굴이 서로 가장자리를 공유하는 것으로 알려진 유일한 두 개의 다면체다.

f면이 있는 다면체를 h구멍으로 표면 위에 박아 각 면이 서로 가장자리를 공유하는 방식으로 박혀 있으면, 그것은 다음과 같은 오일러 특성의 어떤 조작에 의해 나타난다.

${\displaystyle h={\frac {(f-4)(f-3)}{12}.}$

이 방정식은 h = 0, f = 4인 사면체 및 h = 1 및 f = 7인 질라시 다면체에 대해 만족된다.

다음으로 가능한 용액인 h = 6과 f = 12는 정점 44와 가장자리 66을 가진 다면체에 해당된다.그러나 이러한 다면체가 (추상적인 폴리토프보다는) 자기 교차 없이 기하학적으로 실현될 수 있을지는 알 수 없다.보다 일반적으로 이 방정식은 f가 0, 3, 4, 7 modulo 12에 합치될 때 정확하게 충족될 수 있다.^[2][3]

역사

실라시 다면체는 1977년 발견한 헝가리 수학자 라조스 실라시의 이름을 따서 지은 것이다.^[4][1]실라시 다면체에 대한 이중인 Csasarhr 다면체는 Akos Csaszarr (1949년)에 의해 이전에 발견되었는데, 7개의 정점, 모든 정점 쌍을 연결하는 21개의 가장자리, 14개의 삼각형 면을 가지고 있다.실라시 다면체처럼, Csasarr 다면체도 토오루스의 토폴로 되어 있다.^[5]

참조

외부 링크

• Ace, Tom, The Szilassi polyhedron.
• Peterson, Ivars (2007), "A polyhedron with a hole", MathTrek, Mathematical Association of America.
• Weisstein, Eric W., "Szilassi Polyhedron", MathWorld
• Szilassi Polyhedron – Papercraft 모델(CutOutFoldUp.com