꼭지점 구성

Vertex configuration
Icosidodecahedron.png
이코시다데카헤드론 		Icosidodecahedron vertfig labeled.png
로 표현되는 정점 수
3.5.3.5 또는 (3.5)2

기하학에서 정점 구성은[1][2][3][4] 다면체 또는 정점 주위의 면의 순서로 타일링의 정점 형상을 나타내기 위한 속기법이다. 균일한 다면체의 경우 정점 유형은 하나만 있으므로 정점 구성은 다면체를 완전히 정의한다. (치랄 다면체는 동일한 정점 구성을 가진 미러-이미지 쌍에 존재한다.)

정점 구성은 정점 주위를 도는 면의 면 수를 나타내는 일련의 숫자로 주어진다. "a.b.c"라는 표기법은 주위에 3개의 면이 있고, 면에 a, b, c 면이 있는 정점을 나타낸다.

예를 들어, "3.5.3.5"는 4개의 면에 속하는 정점, 즉 삼각형과 펜타곤을 번갈아 나타낸다. 이 정점 구성은 정점-변환성 이코시다헤드론을 정의한다. 표기법은 주기적이며 따라서 출발점이 서로 다르므로 3.5.3.5는 5.3.5.3과 동일하다. 순서가 중요하므로 3.3.5.5는 3.5.3.5와 다르다. (첫 번째 삼각형 2개와 펜타곤 2개가 뒤따른다.) 반복된 원소는 지수로 수집할 수 있으므로 이 예는 (3.5)로도 표현된다.2

정점 설명,[5][6][7] 정점 유형,[8][9] 정점 기호,[10][11] 정점 배열,[12] 정점 패턴,[13] 면 벡터 등으로 다양하게 불려왔다.[14] 1952년 저서 '수학적 모델'에서 아르키메데스 고형물의 용어로 '쿤디와 롤렛'의 상징으로도 불린다.[15][16][17]

꼭지점 수치

정점 구성은 정점 주위의 얼굴을 보여주는 다각형 정점 그림으로도 나타낼 수 있다. 이 꼭지점 그림은 얼굴이 다면체에는 동일한 평면에 있지 않기 때문에 3차원 구조를 가지지만, 정점 통일형 다면체의 경우 모든 인접 정점이 동일한 평면에 있으므로 이 평면 투영을 사용하여 정점 구성을 시각적으로 나타낼 수 있다.

변동 및 용도

일반q 꼭지점 수치 네트, {p,q} = p
Polyiamond-3-1.svg
{3,3} = 33
결함 180° 		Polyiamond-4-1.svg
{3,4} = 34
결함 120° 		Polyiamond-5-4.svg
{3,5} = 35
결함 60° 		Polyiamond-6-11.svg
{3,6} =

36
결함 0°

TrominoV.jpg
{4,3}
결함 90° 		Square tiling vertfig.png
{4,4} =

44
결함 0°

Pentagon net.png
{5,3} = 53
결함 36° 		Hexagonal tiling vertfig.png
{6,3} =

63
결함 0°

정점에는 최소한 세 개의 면과 각도의 결점이 필요하다.
0° 각도의 결함은 유클리드 평면을 일반 타일링으로 채울 것이다.
데카르트의 정리로는 정점수가 720°/결점(4 ( 라디안/결점)이다.

쉼표(,)와 마침표(.) 구분 기호를 사용하는 경우도 있다. 마침표 연산자는 제품과 지수 표기법을 사용할 수 있는 것처럼 보이기 때문에 유용하다. 예를 들어 3.5.3.5를 (3.5)로 표기하기도 한다.2

이 표기법은 또한 일반 다면체의 단순한 슐레플리 기호의 확장된 형태라고 볼 수 있다. 슐레플리 표기법 {p,q}은 각 꼭지점 주위의 q-gon을 의미한다. {p,q}은(는) pp.p로 쓸 수 있도록... (q배수) 또는 pq. 예를 들어, 이코사면체는 {3,5} = 3.3.3.3 또는 3이다5.

이 표기법은 다면체뿐만 아니라 다각형 기울기에도 적용된다. 평면 정점 구성은 비 평면 정점 구성이 동일한 다면체를 나타내는 것과 마찬가지로 균일한 타일을 나타낸다.

키랄 형태에 대해서는 표기법이 애매하다. 예를 들어, 스너브 큐브는 시계 방향과 시계 반대 방향의 형태를 가지며, 미러 이미지에서 동일하다. 둘 다 3.3.3.4 꼭지점 구성을 가지고 있다.

별 다각형

이 표기법은 또한 비콘벡스 정규 면인 항성 다각형에도 적용된다. 예를 들어, 펜타그램에는 중앙을 두 번 도는 5개의 면이 있다는 뜻의 {5/2} 기호가 있다.

예를 들어, 정규 다각형 또는 항성 다각형 정점 형상을 가진 4개의 정규 별 다면체가 있다. 작은 구멍이 있는 도데카헤드론은 명시적 꼭지점 구성 5/2.5/2.5/2.5/2.5/2.5/2/2.5/2로 확장되거나 (5/2)로 결합된 {5/2,5}의 Schléfli 기호를 가지고 있다.5 큰 도마뱀자리 {5/2,3}은(는) 삼각 정점 모양과 구성(5/2.5/2/2) 또는 (5/2)을 가지고 있다.3 위대한 도데카헤드론, {5,5/2}은(는) 펜타그램 정점 수치를 가지며, 정점 구성은 (5.5.5.5.5)/2 또는5 (5)/2이다. 큰 이코사면체, {3,5/2}도 정점 구성(3.3.3.3)/2 또는5 (3)/2와 함께 펜타그램 정점 수치를 가진다.

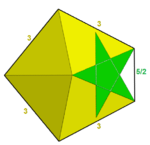Small stellated dodecahedron vertfig.png Great stellated dodecahedron vertfig.png Great snub icosidodecahedron vertfig.png Great retrosnub icosidodecahedron vertfig.png Small retrosnub icosicosidodecahedron vertfig.png
{5/2,5} = (5/2)5 {5/2,3} = (5/2)3 34.5/2 34.5/3 (34.5/2)/2
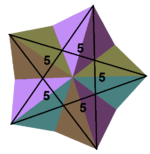Great dodecahedron vertfig.png Great icosahedron vertfig.svg DU57 facets.png DU72 facets.png DU74 facets.png
{5,5/2} = (55)/2 {3,5/2} = (35)/2 V.34.5/2 V34.5/3 V(34.5/2)/2

반전 다각형

정점 도형의 면은 한 방향으로 진행되는 것으로 간주된다. 일부 균일한 다면체에는 얼굴이 역행하는 반전이 있는 정점형상이 있다. 정점 그림은 p<2q, 여기서 p는 변의 수이고 q는 원을 도는 q와 같은 변의 별 폴리곤 표기법에서 이를 나타낸다. 예를 들어 "3/2"는 정점이 두 번 도는 삼각형을 의미하며, 이는 한 번 뒤로 도는 것과 같다. 이와 유사하게 "5/3"은 거꾸로 된 5/2 펜타그램이다.

일반 볼록 폴리곤의 모든 균일한 꼭지점 구성

참고 항목: Archimedenes_solid § 분류, 정규 다각형에 의한 타일링 § 정점에서 만날 수 있는 일반 다각형의 조합 및 균일한 타일링 § 확장된 목록

반정형 다면체는 양의 각도 결함을 가진 정점 구성을 가지고 있다.

참고: 정점 수치는 결함이 0일 경우 평면의 정규 또는 반정맥 타일링을 나타낼 수 있다. 쌍곡선의 결점이 음성이면 쌍곡면의 타일링을 나타낼 수 있다.

균일한 다면체의 경우, 각도 결함을 사용하여 정점 수를 계산할 수 있다. 데카르트의 정리는 위상학 구에 있는 모든 각도 결함은 4˚ 라디안 또는 720도에 합해져야 한다고 명시하고 있다.

균일한 폴리헤드라는 모든 정점을 가지고 있기 때문에, 이 관계를 통해 정점의 수를 계산할 수 있는데, 정점의 수는 4㎛/불량 또는 720/불량이다.

예: 잘린 입방체 3.8.8의 각도 결함은 30도 입니다. 따라서 720/30 = 24 정점을 가진다.

특히 {a,b}에는 4 / (2 - b(1 - 2/a) 정점이 있다.

열거된 모든 정점 구성은 잠재적으로 반정형 다면체를 고유하게 정의한다. 그러나 모든 구성이 가능한 것은 아니다.

위상학적 요건은 존재를 제한한다. 특히 p.q.r은 p-곤이 q-곤과 r-곤을 교대로 둘러싸고 있다는 것을 의미하므로 p가 짝수이거나 q가 r과 같다는 것을 의미한다. 마찬가지로 q는 짝수 또는 p는 r, r은 짝수 또는 p는 q이다. Therefore, potentially possible triples are 3.3.3, 3.4.4, 3.6.6, 3.8.8, 3.10.10, 3.12.12, 4.4.n (for any n>2), 4.6.6, 4.6.8, 4.6.10, 4.6.12, 4.8.8, 5.5.5, 5.6.6, 6.6.6. 사실, 각각의 꼭지점에서 세 개의 얼굴이 만나는 이 모든 구성이 존재하는 것으로 밝혀졌다.

괄호 안의 숫자는 각도 결함에 의해 결정되는 정점의 수입니다.

삼배
4배
5중주
6분의 1배

면 구성

롬빅 도데카헤드론

바이피라미드와 트라페조헤드라를 포함한 균일한 이중 또는 카탈로니아 고형물은 수직으로 규칙적이므로(얼굴-변환성) 때로는 얼굴 구성이라고 하는 유사한 표기법으로 식별할 수 있다.[3] Cundy와 Rollett는 이러한 이중 기호 앞에 V자를 붙였다. 이와는 대조적으로 틸링과 패턴은 등면 기울기의 기호 주위에 대괄호를 사용한다.

이 표기법은 얼굴 주위의 각 꼭지점에 존재하는 얼굴 수의 순차적인 카운트를 나타낸다.[18] 예를 들어, V3.4.3.4 또는 V(3.4)2는 얼굴-변환적인 Rhombic dodecheadron을 나타낸다. 모든 얼굴은 Rhombus이고, Rhombus의 교대 정점에는 각각 3, 4개의 면이 있다.

메모들

  1. ^ Wayback Machine(1993)에 보관된 2015-11-27에 대한 균일한 폴리헤드라를 위한 솔루션
  2. ^ 제복 폴리헤드라 로마 E. 메더(1995)
  3. ^ a b Quasicrystals 결정학: Walter Stewer, Sofia Deloudi, (2009) 페이지 18-20 및 51-53
  4. ^ 물리 금속: 3권 세트, 1권 David E. Lauglin, (2014) 페이지 16–20
  5. ^ 아르키메데스 폴리에드라 스티븐 더치
  6. ^ 유니폼 폴리헤드라 짐 맥닐
  7. ^ 유니폼 폴리헤드라 및 듀얼스 로베르 웹
  8. ^ 플라토닉 및 아르키메데스 고형분의 대칭형 그래프, 쥬리 코비치(2011)
  9. ^ 3. 일반론: 정규 및 준정규 틸링스 케빈 미첼, 1995
  10. ^ 이산수학 티칭에 필요한 리소스: 브라이언 홉킨스가 편집한 강의실 프로젝트, 역사, 모듈 및 기사
  11. ^ 정점 기호 로버트 휘태커
  12. ^ 설계의 구조 및 양식: 마이클 한의 창의적 실천을 위한 비판적 아이디어
  13. ^ 플라토닉과 아르키메데스 고체 주리 코비치의 대칭형 그래프
  14. ^ Deza, Michel; Shtogrin, Mikhail (1999). "Uniform Partitions of 3-space, their Relatives and Embedding". arXiv:math/9906034. Bibcode:1999math......6034D. {{cite journal}}: Cite 저널은 필요로 한다. journal= (도움말)
  15. ^ Weisstein, Eric W. "Archimedean solid". MathWorld.
  16. ^ 분할된 구체: 지리학 및 구 6.4.1 Cundy-Rollett 기호의 질서정연한 하위 구분, 페이지 164
  17. ^ 러플린(2014), 페이지 16
  18. ^ 쿤디와 롤렛(1952년)

참조

  • Cundy, H. and Rollett, A, Mathemical Models (1952년), (제3판, 1989년 영국 Stradbroke: 타킨 펍), 3.7 아르키메데스 폴리헤드라. 페이지 101–115, 페이지 118–119 표 I, 아르키메데스 듀얼의 네트, V.a.b.c... 세로로 고정된 기호로
  • Peter Cromwell, Polyedra, Cambridge University Press (1977) Archimedeans 고형물. 156-167 페이지
  • Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. Cundy-Rollett 기호를 사용한다.
  • Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. 페이지 58–64, 일반 다각형 기울기 A.B.c.... (일반 다각형과 별 다각형에 의한 기울기) 페이지 95–97, 176, 283, 614–620, 모노헤드랄 타일링 기호 [v1.v2. ...vr] 페이지 632–642 빈 틸팅.
  • 2008년 사물의 대칭, 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, ISBN 978-1-56881-220-5 (p. 289 정점 수치, 아르키메데스 고형물과 기울기에 쉼표 구분기 사용)

외부 링크