사각뿔

사각뿔
사각뿔
유형	존슨; J92 – J – J12 – J
얼굴들	4개의 삼각형; 1제곱
가장자리	8
꼭짓점	5
꼭짓점 구성
대칭군
용량
이중 다면체	자기의
특성.	볼록한
그물

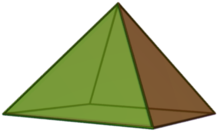
기하학에서 사각뿔은 밑면이 사각형인 피라미드로, 총 5개의 면을 가지고 있습니다. 피라미드의 꼭지점이 정사각형의 중심 바로 위에 있다면 이등변삼각형이 4개인 직각 사각뿔이고, 그렇지 않으면 비스듬한 사각뿔입니다. 피라미드의 모든 모서리의 길이가 같을 때 삼각형은 모두 정방형이며, 이를 정방형 사각뿔이라고 합니다.

정사각형 피라미드는 건축의 역사를 통틀어 등장했는데, 이집트 피라미드와 다른 많은 유사한 건물들을 예로 들 수 있습니다. 사각 피라미드 분자 구조의 화학에서도 발생합니다. 정사각형 피라미드는 종종 다른 다면체의 건설에 사용됩니다. 고대의 많은 수학자들은 다양한 접근법으로 정사각형 피라미드의 부피에 대한 공식을 발견했습니다.

특성.

직각 정사각뿔

정사각형 피라미드는 다섯 개의 꼭짓점, 여덟 개의 모서리, 다섯 개의 면을 가지고 있습니다. 피라미드의 밑면이라고 불리는 한 면은 정사각형이고, 다른 네 면은 삼각형입니다.^[3] 네 개의 모서리는 네 개의 꼭짓점을 연결하여 정사각형을 구성합니다. 나머지 네 개의 가장자리는 피라미드의 측면 가장자리로 알려져 있습니다; 그것들은 꼭지점이라고 불리는 다섯 번째 꼭지점에서 만납니다.^[4] 피라미드의 꼭짓점이 정사각형의 중심으로부터 수직으로 세워진 선 위에 놓여 있으면, 이를 직각 사각뿔이라고 하며, 네 개의 삼각형 면은 이등변삼각형입니다. 그렇지 않은 경우, 피라미드는 두 개 이상의 비이등변 삼각형 면을 가지며 비스듬한 사각뿔이라고 불립니다.^[5]

모든 삼각형의 모서리의 길이가 같고, 네 개의 삼각형이 정삼각형이고, 피라미드의 면이 모두 정다각형이라면 정삼각형입니다.^[6] 인접한 삼각형 면 사이의 다면체 $\arccos \left(-1/3\right)\approx 109.47^{\circ }$ 는 $\arccos \left(-1/3\right)\approx 109.47^{\circ }$ ⁡ $($ - 1 / $3$ ) ≈ $109$ .47 ∘ {\displaystyle \ $arcos$ \left $(-1$ /3\ $right)\$ 약 109.47^{\circuit}}이며, 바닥과 각 삼각형 면 사이의 각도는 arcan ⁡ 2 ≈ 54.735 ∘ {\displaystyle \acrt {\sqrt {2}\약 54.735^{\circuit}}입니다. 정다각형만 면으로 하는 볼록한 다면체를 존슨 입체라고 하고, 정방형의 $J_{1}$ 은 $J_{1}$ 1 {\ $displaystyle J_{$ 1}}로 열거된 최초의 존슨 입체입니다 $J_{1}$ ^[7] 정다각형을 밑면으로 하는 다른 직각뿔들처럼, 직각 사각뿔도 피라미드 대칭을 갖습니다. 정사각형 피라미드의 경우, 이것은 순환군 $C_{4v}$ 4 $C_{4v}$ ${\$ 의 대칭입니다 $C_{4v}$ 피라미드는 대칭축을 중심으로 한 전체 회전의 1, 2, 3/4로 회전하여 불변 상태로 유지됩니다. 또한 기저부의 이등분선을 통과하는 수직면에 대해 거울 대칭입니다.^[1] 휠 그래프 $W_{4}$ $W_{4}$ ${\$ 로 나타낼 수 있으며 $W_{4}$ 일반적으로 휠 $W_{n}$ W ${\$ W_{ $n}}$ 는 {\ $displaystyle$ n $}면$ 피라미드의 $n$ $n$ 을 나타냅니다 $W_{n}$ .^[8]

표면적과 부피

직각 사각뿔의 $s$ 경사 $높이$ $s$ 는 이등변 삼각형 중 하나의 높이로 정의됩니다. 피타고라스 정리를 통해 얻을 수 있습니다.

s={\sqrt {b^{2}-{\frac {l^{2}}{4}}}},

여기서

l

l

은

l

사각형의 모서리 중 하나인 삼각형의 밑변의 길이이고,

b

b

는

b

피라미드의 측면 모서리인 삼각형의 다리 길이입니다.^[9] 직각 사각뿔의

h

높이

h

{\displaystyle

h

}

도 마찬가지로 구할 수 있으며, 경사 높이 공식을 대입하면 다음과 같습니다.^[10]

h={\sqrt {s^{2}-{\frac {l^{2}}{4}}}}={\sqrt {b^{2}-{\frac {l^{2}}{2}}}}.

다면체의 표면적은 다면체의 표면적의 합입니다. 직각 사각뿔의 표면적

A

A

는

A=4T+S

=

A=4T+S

A=4T+S

+ S

{\

displaystyle

A = 4 T + S

}

로 표현할 수 있으며, 여기서 T {\displaystyle T} 및 S {\displaystyle S}는 각각 삼각형과 밑면 중 하나의 면적입니다. 삼각형의 넓이는 밑변과 변의 곱의 절반이고, 정사각형의 넓이는 변의 길이입니다. 이는 다음과 같은 표현을 제공합니다.^[11]

A=4\left({\frac {1}{2}}ls\right)+l^{2}=2ls+l^{2}.

일반적으로 피라미드의

V

볼륨

V

V

는 밑면 면적의 1/3에 높이를 곱한 것과 같습니다.^[12] 정사각형 피라미드의 공식으로 표현하면 다음과 같습니다.^[13]

V={\frac {1}{3}}l^{2}h.

많은 수학자들이 고대에 정사각형 피라미드의 부피를 계산하는 공식을 발견했습니다. 이집트 수학자들은 모스크바 수학 파피루스에서 잘린 사각뿔의 부피를 계산하는 공식에 대한 지식을 증명했는데, 이 공식이 어떻게 유도되었는지는 알 수 없습니다. 사각뿔의 부피를 발견하는 것을 넘어 사각뿔의 기울기와 높이를 구하는 문제는 Rhind Mathematical Papyrus에서 찾을 수 있습니다.^[14] 바빌로니아 수학자들은 또한 좌절의 부피를 고려했지만 그것에 대한 잘못된 공식을 제시했습니다.^[15] 중국의 수학자 류후이도 직사각형의 고체를 조각으로 쪼개는 방법으로 부피를 발견했습니다.^[16]

적용들

이집트 피라미드는 건축에서 정사각형 피라미드 건물의 한 예입니다.

이집트와 비슷한 건물인 메소아메리카 피라미드 중 하나는 평평한 꼭대기와 얼굴에 계단이 있습니다.

건축에서 고대 이집트에 지어진 피라미드는 정사각형 피라미드 모양의 건물의 예입니다.^[17] 피라미드학자들은 기자 피라미드의 설계를 위해 케플러 삼각형과 황금비율에 기초한 이론을 포함한 다양한 제안들을 내놓았습니다. 그러나 현대 학자들은 이집트 수학과 비율에 대한 지식과 더 일치하기 때문에 정수비를 사용한 설명을 선호합니다.^[18] 메소아메리카 피라미드는 이집트와 비슷한 고대 피라미드 건축물이기도 합니다; 평평한 꼭대기와 얼굴을 올라가는 계단이 있다는 점에서 다릅니다.^[19] 이집트 피라미드를 모방한 디자인의 현대식 건물로는 루브르 피라미드와 카지노 호텔인 룩소 라스베가스가 있습니다.^[20]

입체화학에서 원자단은 정사각형 피라미드 기하학을 가질 수 있습니다. 사각뿔형 분자는 하나의 활성 론 쌍을 갖는 주군 원소를 가지고 있는데, VSEPR 이론으로 알려진 분자의 기하학을 예측하는 모델로 설명할 수 있습니다.^[21] 이러한 구조를 가진 분자의 예로는 염소 5불화물, 브롬 5불화물, 요오드 5불화물 등이 있습니다.^[22]

정사각형 피라미드의 밑면을 다른 다면체의 정사각형 면에 부착하여 새로운 다면체를 구성할 수 있는데, 이는 증강의 한 예입니다. 예를 들어 정육면체의 각 면에 정사각뿔의 밑면을 붙이면 테트라키스 육면체를 만들 수 있습니다.^[23] 피라미드에 프리즘이나 안티프리즘을 붙이는 것을 각각 신장 또는 자이로 신장이라고 합니다.^[24] 다른 존슨 고체 중 일부는 정사각형 피라미드를 증강하거나 정사각형 피라미드로 다른 모양을 증강함으로써 구성할 수 있습니다: 길쭉한 정사각형 $J_{8}$ J 8 $J_{8}$ {\ $displaystyle J_{8$ 자이로길쭉한 정사각형 $J_{10}$ $J_{10}$ 10 $J_{10}$ {\ $displaystyle J_{10$ 길쭉한 정사각형 이중 피라미드 $J_{15}$ $J_{15}$ ${\$ gyroelongated square bipyramid $J_{17}$ , augmented triangular prism $J_{49}$ , biaugmented triangular prism $J_{50}$ , triaugmented triangular prism $J_{51}$ , augmented pentagonal prism $J_{52}$ , biaugmented pentagonal prism $J_{53}$ , augmented hexagonal prism $J_{54}$ , parabiaugmented hexagonal prism $J_{55}$ , metabiaugmented hexagonal prism $J_{56}$ , 3증강 육각 프리즘 $J_{57}$ $J_{57}$ ${\$ 증강 스피노코로나 J $J_{87}$ ${\$ ^[25]

참고 항목

정사각형 피라미드 수, 정사각형 피라미드에 쌓인 구의 개수를 세는 자연수.

메모들

^ ^a ^b ^c 존슨 (1966).
^ Wohlleben (2019), p. 485–486.
^ Cissold (2020), p. 180.
^ O'Keeffe & Hyde (2020), p. 141; Smith (2000), p. 98.
^ Freitag(2014), 페이지 598.
^ Hocevar (1903), p. 44.
^ 우에하라 (2020), 62쪽.
^ Pisanski & Servatius (2013), 21쪽.
^ Larcombe (1929), p. 177; Perry & Perry (1981), pp. 145–146.
^ 라콤 (1929), 177쪽.
^ Freitag(2014), p. 798
^ Alexander & Koeberlin (2014), 403쪽.
^ 라콤 (1929), 178쪽.
^ Cromwell (1997), pp. 20–22.
^ 이브(1997), 2쪽.
^ 바그너 (1979).
^ Kinsey, Moore & Prassidis (2011), p. 371.
^ Herz-Fischler(2000)는 이 피라미드의 모양에 대한 많은 대안적인 이론들을 조사했습니다. 케플러 삼각형에 특정한 자료는 11장 "케플러 삼각형 이론", 80~91쪽, "이론은 고대 이집트인들에게 알려진 것과 일치하는 수학 수준에 해당해야 한다"는 원칙에 의해 케플러 삼각형 이론을 제거할 수 있다는 결론은 166쪽을 참조하십시오. 이 삼각형에 대한 케플러의 연구 역사는 노트 3, 페이지 229를 참조하십시오. 로시(2004 ), 페이지 67-68을 참조하십시오. "고대 이집트의 어떤 기록된 수학적 출처에도 황금 섹션으로 분류될 수 있는 산술 계산이나 기하학적 구조에 대한 직접적인 증거는 없습니다. $\varphi$ φ $displaystyle$ \varphi} 및 φ ${\displaystyle$ \varphi} 자체에 대한 수렴, 숫자로, 현존하는 중세의 수학적 출처와 맞지 않음"; 피라미드의 모양과 다른 이집트 건축물에 대한 여러 대안 이론에 대한 광범위한 논의도 참조하십시오, 7-56쪽. Rossi & Tout(2002)과 Markowsky(1992)도 참조하십시오.
^ Feder(2010), p. 34; Takacs & Cline(2015), p. 16.
^ Jarvis & Naested (2012), p. 172; Simonson (2011), p. 154.
^ Petrucci, Harwood & Herring (2002), 414쪽.
^ Emeléus (1969), p. 13.
^ Demey & Smessaert (2017).
^ 슬로보단, 오브라도비치, ð우카노비치 (2015).
^ Rajwade (2001), pp. 84–89. 표 12.3을 참조하십시오. 여기서 $P_{n}$ ${\$ 는 $n$ $n$ $면$ 프리즘을 $n$ 나타내고 An $P_{n}$ ${\$ 면 $n$ $n$ 을 나타냅니다 $A_{n}$ .

참고문헌

Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Elementary Geometry for College Students (6th ed.). Cengage Learning. ISBN 978-1-285-19569-8.
Clissold, Caroline (2020). Maths 5–11: A Guide for Teachers. Taylor & Francis. ISBN 978-0-429-26907-3.
Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 978-0-521-55432-9.
Demey, Lorenz; Smessaert, Hans (2017). "Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation". Symmetry. 9 (10): 204. Bibcode:2017Symm....9..204D. doi:10.3390/sym9100204.
Emeléus, H. J. (1969). The Chemistry of Fluorine and Its Compounds. Academic Press. ISBN 978-1-4832-7304-4.
Eves, Howard (1997). Foundations and Fundamental Concepts of Mathematics (3rd ed.). Dover Publications. ISBN 978-0-486-69609-6.
Feder, Kenneth L. (2010). Encyclopedia of Dubious Archaeology: From Atlantis to the Walam Olum: From Atlantis to the Walam Olum. ABC-CLIO. ISBN 978-0-313-37919-2.
Freitag, Mark A. (2014). Mathematics for Elementary School Teachers: A Process Approach. Brooks/Cole. ISBN 978-0-618-61008-2.
Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0-88920-324-5.
Hocevar, Franx (1903). Solid Geometry. A. & C. Black.
Jarvis, Daniel; Naested, Irene (2012). Exploring the Math and Art Connection: Teaching and Learning Between the Lines. Brush Education. ISBN 978-1-55059-398-3.
Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
Kinsey, L. Christine; Moore, Teresa E.; Prassidis, Efstratios (2011). Geometry and Symmetry. John Wiley & Sons. ISBN 978-0-470-49949-8.
Larcombe, H. J. (1929). Cambridge Intermediate Mathematics: Geometry Part II. Cambridge University Press.
Markowsky, George (1992). "Misconceptions about the Golden Ratio" (PDF). The College Mathematics Journal. Mathematical Association of America. 23 (1): 2–19. doi:10.2307/2686193. JSTOR 2686193. Retrieved 29 June 2012.
O'Keeffe, Michael; Hyde, Bruce G. (2020). Crystal Structures: Patterns and Symmetry. Dover Publications. ISBN 978-0-486-83654-6.
Perry, O. W.; Perry, J. (1981). Mathematics. Springer. doi:10.1007/978-1-349-05230-1. ISBN 978-1-349-05230-1.
Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry: Principles and Modern Applications. Vol. 1. Prentice Hall. ISBN 978-0-13-014329-7.
Pisanski, Tomaž; Servatius, Brigitte (2013). Configuration from a Graphical Viewpoint. Springer. doi:10.1007/978-0-8176-8364-1. ISBN 978-0-8176-8363-4.
Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge University Press. pp. 67–68.
Rossi, Corinna; Tout, Christopher A. (2002). "Were the Fibonacci series and the Golden Section known in ancient Egypt?". Historia Mathematica. 29 (2): 101–113. doi:10.1006/hmat.2001.2334. hdl:11311/997099.
Simonson, Shai (2011). Rediscovering Mathematics: You Do the Math. Mathematical Association of America. ISBN 978-0-88385-912-4.
Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms" (PDF). Journal for Geometry and Graphics. 19 (1): 79–91.
Smith, James T. (2000). Methods of Geometry. John Wiley & Sons. ISBN 0-471-25183-6.
Takacs, Sarolta Anna; Cline, Eric H. (2015). The Ancient World. Routledge. p. 16. ISBN 978-1-317-45839-5.
Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
Wagner, Donald Blackmore (1979). "An early Chinese derivation of the volume of a pyramid: Liu Hui, third century A.D.". Historia Mathematics. 6 (2): 164–188. doi:10.1016/0315-0860(79)90076-4.
Wohlleben, Eva (2019). "Duality in Non-Polyhedral Bodies Part I: Polyliner". In Cocchiarella, Luigi (ed.). ICGG 2018 – Proceedings of the 18th International Conference on Geometry and Graphics: 40th Anniversary – Milan, Italy, August 3–7, 2018. International Conference on Geometry and Graphics. Springer. doi:10.1007/978-3-319-95588-9. ISBN 978-3-319-95588-9.

외부 링크

Weisstein, Eric W., "Square pyramid" ("Johnson solid") at MathWorld.
Weisstein, Eric W. "Wheel graph". MathWorld.
정사각형 피라미드 – 상호 작용 다면체 모형
가상 현실 다면체 georgehart.com : 폴리헤드라 백과사전(VRML 모델)

[FOOTNOTEJohnson1966-1] 존슨 (1966).

[FOOTNOTEWohlleben2019[httpsbooksgooglecombooksidrEpjDwAAQBAJpgPA485_485–486]-2] Wohlleben (2019), p. 485–486.

[FOOTNOTEClissold2020[httpsbooksgooglecombooksidXgW5DwAAQBAJpgPA180_180]-3] Cissold (2020), p. 180.

[FOOTNOTEO'KeeffeHyde2020[httpsbooksgooglecombooksid_MjPDwAAQBAJpgPA141_141]Smith2000[httpsbooksgooglecombooksidB0khWEZmOlwCpgPA98_98]-4] O'Keeffe & Hyde (2020), p. 141; Smith (2000), p. 98.

[FOOTNOTEFreitag2014[httpsbooksgooglecombooksidGYsWAAAAQBAJpgPA598_598]-5] Freitag(2014), 페이지 598.

[FOOTNOTEHocevar1903[httpsbooksgooglecombooksid0OAXAAAAYAAJpgPA44_44]-6] Hocevar (1903), p. 44.

[FOOTNOTEUehara2020[httpsbooksgooglecombooksid51juDwAAQBAJpgPA62_62]-7] 우에하라 (2020), 62쪽.

[FOOTNOTEPisanskiServatius2013[httpsbooksgooglecombooksid3vnEcMCx0HkCpgPA21_21]-8] Pisanski & Servatius (2013), 21쪽.

[FOOTNOTELarcombe1929[httpsbooksgooglecombooksidSAE9AAAAIAAJpgPA177_177]PerryPerry1981[httpsbooksgooglecombooksidDi2uCwAAQBAJpgPA145_145–146]-9] Larcombe (1929), p. 177; Perry & Perry (1981), pp. 145–146.

[FOOTNOTELarcombe1929[httpsbooksgooglecombooksidSAE9AAAAIAAJpgPA177_177]-10] 라콤 (1929), 177쪽.

[FOOTNOTEFreitag2014[httpsbooksgooglecombooksidGYsWAAAAQBAJpgPA798_798]-11] Freitag(2014), p. 798

[FOOTNOTEAlexanderKoeberlin2014[httpsbooksgooglecombooksidEN_KAgAAQBAJpgPA403_403]-12] Alexander & Koeberlin (2014), 403쪽.

[FOOTNOTELarcombe1929[httpsbooksgooglecombooksidSAE9AAAAIAAJpgPA178_178]-13] 라콤 (1929), 178쪽.

[FOOTNOTECromwell1997[httpsarchiveorgdetailspolyhedra0000crompage20mode2upviewtheater_20–22]-14] Cromwell (1997), pp. 20–22.

[FOOTNOTEEves1997[httpsbooksgooglecombooksidJ9QcmFHj8EwCpgPA2_2]-15] 이브(1997), 2쪽.

[FOOTNOTEWagner1979-16] 바그너 (1979).

[FOOTNOTEKinseyMoorePrassidis2011[httpsbooksgooglecombooksidfFpuDwAAQBAJpgRA1-PA371_371]-17] Kinsey, Moore & Prassidis (2011), p. 371.

[18] Herz-Fischler(2000)는 이 피라미드의 모양에 대한 많은 대안적인 이론들을 조사했습니다. 케플러 삼각형에 특정한 자료는 11장 "케플러 삼각형 이론", 80~91쪽, "이론은 고대 이집트인들에게 알려진 것과 일치하는 수학 수준에 해당해야 한다"는 원칙에 의해 케플러 삼각형 이론을 제거할 수 있다는 결론은 166쪽을 참조하십시오. 이 삼각형에 대한 케플러의 연구 역사는 노트 3, 페이지 229를 참조하십시오. 로시(2004 ), 페이지 67-68을 참조하십시오. "고대 이집트의 어떤 기록된 수학적 출처에도 황금 섹션으로 분류될 수 있는 산술 계산이나 기하학적 구조에 대한 직접적인 증거는 없습니다. $\varphi$ φ $displaystyle$ \varphi} 및 φ ${\displaystyle$ \varphi} 자체에 대한 수렴, 숫자로, 현존하는 중세의 수학적 출처와 맞지 않음"; 피라미드의 모양과 다른 이집트 건축물에 대한 여러 대안 이론에 대한 광범위한 논의도 참조하십시오, 7-56쪽. Rossi & Tout(2002)과 Markowsky(1992)도 참조하십시오.

[FOOTNOTEFeder2010[httpsbooksgooglecombooksidRlRz2symkAsCpgPA34_34]TakacsCline2015[httpsbooksgooglecombooksidSPcvCgAAQBAJpgPA16_16]-19] Feder(2010), p. 34; Takacs & Cline(2015), p. 16.

[FOOTNOTEJarvisNaested2012[httpsbooksgooglecombooksidNWzsz8vioZwCpgPA172_172]Simonson2011[httpsbooksgooglecombooksid56Mlw0ick2YCpgPA154_154]-20] Jarvis & Naested (2012), p. 172; Simonson (2011), p. 154.

[FOOTNOTEPetrucciHarwoodHerring2002[httpsbooksgooglecombooksidEZEoAAAAYAAJpgPA414_414]-21] Petrucci, Harwood & Herring (2002), 414쪽.

[FOOTNOTEEmeléus1969[httpsbooksgooglecombooksid9SkSBQAAQBAJpgPA13_13]-22] Emeléus (1969), p. 13.

[FOOTNOTEDemeySmessaert2017-23] Demey & Smessaert (2017).

[FOOTNOTESlobodanObradovićÐukanović2015-24] 슬로보단, 오브라도비치, ð우카노비치 (2015).

[25] Rajwade (2001), pp. 84–89. 표 12.3을 참조하십시오. 여기서 $P_{n}$ ${\$ 는 $n$ $n$ $면$ 프리즘을 $n$ 나타내고 An $P_{n}$ ${\$ 면 $n$ $n$ 을 나타냅니다 $A_{n}$ .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

v t 존슨고체
피라미드, 큐폴래, 로툰대	사각뿔 오각뿔 삼각형 큐폴라 네모난 큐폴라 오각형 큐폴라 오각형의 로툰다
수정 피라미드	길쭉한 삼각뿔 길쭉한 사각뿔 길쭉한 오각뿔 자이로 긴 사각뿔 자이로 긴 오각뿔 삼각쌍뿔 모양의 오각형 쌍각형 길쭉한 삼각쌍뿔 모양의 쌍뿔 모양 길쭉한 사각형의 쌍피라미드 길쭉한 오각형 쌍각형 자이로 롱 스퀘어 바이피라미드
수정된 큐폴라 및 로툰대	길쭉한 삼각형 큐폴라 길쭉한 네모난 큐폴라 길쭉한 오각형 큐폴라 길쭉한 오각형의 로툰다 자이로 긴 삼각 큐폴라 자이로 롱 스퀘어 큐폴라 자이로 긴 오각형 큐폴라 자이로 긴 오각형 로툰다 자이로비파스티지움 삼각형의 오소빅 유폴라 사각정육면체 네모난 자이로비쿠폴라 오각정육면체 오각형의 자이로비쿠폴라 오각정육면체의 오각정육면체 오각형 자이로쿠폴라로툰다 오각형의 오각형의 오각형 길쭉한 삼각형의 오르토빅 유폴라 길쭉한 삼각형의 자이로비쿠폴라 길쭉한 네모난 자이로비쿠폴라 길쭉한 오각정육각정형 유폴라 길쭉한 오각형의 자이로비쿠폴라 길쭉한 오각형의 오각형 오각형 오각형 오각형 오각형. 길쭉한 오각형의 자이로쿠폴라로툰다 길쭉한 오각형의 오르토비로툰다 길쭉한 오각형의 자이로비로툰다 자이로긴삼각쌍추꽃 자이로롱 스퀘어 바이큐폴라 길쭉한 오각쌍추꽃 자이로 긴 오각형 큐폴라로툰다 자이로롱오각비로툰다
증강프리즘	증강 삼각 프리즘 쌍대 삼각기둥 3배증삼각기둥 증강 오각 프리즘 쌍대 오각기둥 증강 육각 프리즘 파라증강 육각기둥 대사증강 육각기둥 3배 증강 육각 프리즘
변형 플라톤 고체	증강 십이면체 평행증강십이면체 대사증강십이면체 삼축 십이면체 대사가 감소된 20면체 삼차원 정이십면체 증강된 삼차원 정이십면체
수정된 아르키메데스 고체	증강된 잘린 사면체 증강된 잘린 정육면체 이진화된 잘린 정육면체 증강된 잘린 십이면체 포물선 확대 절단 십이면체 대사증강 절단 십이면체 3배 증강된 절단 십이면체 자이레이트 마름모꼴 정십면체 파라비율 마름모 정십면체 대사율 마름모꼴 정십면체 삼각형 마름모 정이십면체 축소 마름모 십이면체 파라자일레이트 감소 마름모 십이면체 메타기레이트 감소 마름모꼴십이면체 bigyrate diminated rhombicosid 십이면체 파라비디는 마름모꼴 십이면체를 감소시켰습니다. metabidized rombicosid 십이면체 자이레이트 비디미티드 마름모 십이면체 삼배체 마름모 십이면체
초고체	스누브 디스페노이드 무뚝뚝한 반프리즘 sphenocorona 증강된 스페노코로나 sphenomegacorona 헴페노메가코로나 불협화음 빌루나비로툰다 삼각헤브페노로툰다
(분류 가능한 표인 Johnson 고형물 목록도 참조)

Search

사각뿔

네임스페이스

더

목차

특성.

직각 정사각뿔

표면적과 부피

적용들

참고 항목

메모들

참고문헌

외부 링크

사각뿔

유형	존슨 $J 92 - J - J 1 2 - J$
얼굴들	4개의 삼각형 1제곱
가장자리	8
꼭짓점	5
꼭짓점 구성	$4\times (3^{2}\times 4)+1\times (3^{4})$ ^[1]
대칭군	$C_{4v}$
용량	${\frac {1}{3}}l^{2}h$
이중 다면체	자기의^[2]
특성.	볼록한
그물