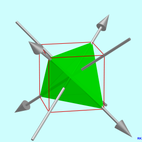
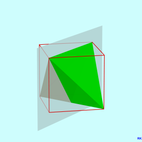
3차원의 점 그룹

3차원의 점 그룹
다면군, [n,3], (*n32)
비자발적 대칭 C_s, (*) [ ] =	순환 대칭 C_nv, (*n) [n] =	치측 대칭 D_nh, (*n22) [n,2] =
사면 대칭 T_d, (*332) [3,3] =	팔면 대칭 O_h, (*432) [4,3] =	이코사면 대칭 I_h, (*532) [5,3] =

기하학에서, 3차원의 점군은 3차원의 등계집단을 의미하며, 원점을 고정하거나 그에 상응하여 구의 등계집단을 유지한다. 직교 그룹 O(3)의 하위 그룹이며, 원점을 고정하거나 그에 상응하여 직교 행렬의 그룹을 그대로 두는 모든 등위계의 그룹이다. O(3) 자체는 모든 등각류 중 유클리드 그룹 E(3)의 하위그룹이다.

물체의 대칭 그룹은 등위계 그룹이다. 따라서 등위계 집단의 분석은 가능한 대칭의 분석이다. 경계 3D 개체의 모든 등각에는 하나 이상의 공통 고정점이 있다. 우리는 그들 중 하나로 기원을 선택한다.

물체의 대칭 그룹은 그것의 회전 그룹이나 적절한 대칭 그룹과 반대로 그것의 전체 대칭 그룹과 3D 공간 자체의 회전 그룹 SO(3)의 교차점과는 반대로 그것의 전체 대칭 그룹이라고도 불린다. 물체의 회전 그룹은 물체가 키랄인 경우에만 전체 대칭 그룹과 동일하다.

동일한 지점을 통과하는 반사 미러 면의 유한 집합에 의해 순수하게 생성되는 점 그룹은 콕시터 표기법으로 표현되는 유한한 콕시터 그룹이다.

3차원의 점군은 화학에서 특히 분자와 공밸런트 결합을 형성하는 분자 궤도의 대칭을 묘사하기 위해 많이 사용되고 있으며, 이러한 맥락에서 분자 점 그룹이라고도 불린다.

그룹 구조

SO(3)는 E(3⁺)의 하위그룹으로, 방향성을 보존하는 직등계로 구성되며, 원점을 고정시킨 것을 포함한다.

O(3)는 SO(3)의 직접적인 산물이며, 역전에 의해 생성된 그룹(매트릭스 -I로 표시됨):

O(3) = SO(3) × { I, -I }

따라서 역전을 통해 모든 직접 등거리와 모든 간접 등거리 사이에 1:1의 일치성이 있다. 또한 O(3)의 모든 직접 등위계 H 그룹과 O(3)의 모든 등위계 그룹 K 그룹 사이에 1 대 1의 대응 관계가 있으며, 이 대응은 다음과 같다.

K = H × { I, -I }

H = K ∩ SO(3)

예를 들어, H가 C인₂ 경우 K가 C인_2h 경우, H가₃ C인 경우 K가 S이다₆(이 그룹의 정의는 아래쪽을 참조하십시오).

직등분계 H 그룹이 지수 2의 부분군 L을 갖는 경우, 역전을 포함하는 해당 그룹 이외에 간접 등분계수를 포함하지만 역전은 없는 해당 그룹도 있다.

M = L ∪ ( (H ∖ L) × { −I } )

여기서 등위계(A, I )는 A와 동일하다. 예를 들면 H의 경우₄ C, M의₄ 경우 S가 있을 것이다.

따라서 M은 H ∖ L의 등위계를 반전시켜 H로부터 얻는다. 이 그룹 M은 H와 마찬가지로 추상 그룹 이소모르퍼시픽이다. 반대로 간접 등위계를 포함하지만 반전하지 않는 모든 등위계 그룹에 대해서는 간접 등위계를 반전시켜 회전 그룹을 얻을 수 있다. 이것은 등위계 그룹을 분류할 때 명확히 하는 것이다. 아래를 참조하십시오.

2D에서 k-폴드 회전 C의_k 순환 그룹은 모든 양의 정수 k에 대해 O(2)와 SO(2)의 정규 부분군이다. 따라서 3D에서 각 축에 대해 해당 축에 대한 k-폴드 회전 순환 그룹은 해당 축에 대한 모든 회전 그룹의 정상 하위 그룹이다. 지수 2의 어떤 부분군은 정상이기 때문에, 회전 그룹(C_n)은 축을 통해 (C_n) 반사면에 추가함으로써 얻은 그룹(C_nv)과 (C_n) 축에 수직인 반사면을 추가하여 얻은 그룹(C_nh) 모두에서 정상이다.

원점을 고정하는 3D 등각도계

그룹 O(3)를 형성하면서 원점을 고정된 상태로 두는 3차원 공간 R의³ 등각도는 다음과 같이 분류할 수 있다.

SO(3):
- 정체성
- 180°와 같지 않은 각도로 원점을 통과하는 축을 중심으로 회전한다.
- 180° 각도로 원점을 통과하는 축의 회전
반전(x는 -x에 매핑됨), 즉, 각각 다음과 같다.
- 역전의
- 축에 수직인 원점을 통과하는 평면에서 반사되는 것과 결합하여 180°와 같지 않은 각도로 축을 중심으로 회전한다.
- 기원을 통과하는 비행기의 반사

특히 4번과 5번, 더 넓은 의미에서 6번도 부적절한 회전이라고 한다.

번역을 포함한 유사한 개요도 참조하십시오.

결합

두 물체의 대칭 유형을 비교할 때 각각에 대해 원점을 선택한다. 즉, 같은 중심을 가질 필요가 없다. 더욱이 두 개체는 대칭군이 O(3)의 결합 부분군일 경우 대칭형이 동일한 것으로 간주된다(그룹 G의 2개 부분군₁ H, H는₂ 결합형일 경우, H₁ = gHg⁻¹₂).

예를 들어, 두 개의 3D 물체는 동일한 대칭 유형을 가지고 있다.

만약 양쪽이 거울 대칭을 가지고 있다면, 그러나 다른 거울 평면에 관해서.
둘 다 3배 회전 대칭이지만 다른 축과 관련된 경우.

다중 미러 평면 및/또는 회전 축의 경우, 첫 번째 대칭 그룹의 전체 구조를 두 번째 대칭 그룹의 구조와 매핑하는 회전이 있는 경우에만 동일한 대칭 유형을 가진다. (사실 그러한 회전은 두 개 이상 있을 것이지만, 거울이나 축이 하나만 있을 때와 같이 무한수는 아닐 것이다.) 결합 정의는 또한 구조물의 거울 이미지를 허용하지만, 이것은 필요하지 않다, 구조 자체가 아키랄이다. 예를 들어, 대칭 그룹이 3배 회전축을 포함하는 경우, 그것은 두 개의 반대 방향으로 회전하는 것을 포함한다. (구조물은 나사 축이 있는 11쌍의 우주 그룹에 대한 치랄이다.)

무한등분군

무한 등위계 집단은 여러 가지가 있다. 예를 들어, 축을 중심으로 비합리적인 회전 수로 회전에 의해 생성되는 "순환 집단"(한 요소에 의해 생성됨 - 비틀림 그룹과 혼동되지 않음)이 있다. 우리는 같은 축을 중심으로 더 많은 회전을 추가함으로써 비 사이클론적인 아벨리아 집단을 만들 수도 있다. 또한 다른 축을 중심으로 회전하여 생성되는 비아벨라 그룹도 있다. 이들은 대개 (일반적으로) 자유 집단이다. 회전은 특별히 선택하지 않는 한 무한할 것이다.

지금까지 언급된 모든 무한 집단은 O(3)의 위상학적 하위집단으로 폐쇄되지 않는다. 우리는 이제 토폴로지적으로 폐쇄된 O(3) 하위그룹에 대해 논의한다.

표시되지 않은 구체는 O(3) 대칭이다.

전체 O(3)는 구형 대칭의 대칭군이며, SO(3)는 해당 회전군이다. 다른 무한등도계 그룹은 원점을 통과하는 축과 축을 통과하는 평면에 추가 반사가 있는 축에 대한 모든 회전 및 축에 수직인 원점을 통과하는 평면에 반사되는 회전으로 구성된다. 축을 통과하는 평면에 반사를 하고 축에 수직인 원점을 통과하는 평면에 반사를 포함하거나 포함하지 않는 것은 두 가지 유형의 원통형 대칭에 대한 대칭 그룹이다. 무한 회전 대칭이 있는 물체는 축을 통해 거울 평면의 대칭도 가질 수 있다는 점에 유의한다.

유한등계 집단의 모든 한계인 7개의 연속 집단이 있다. 소위 제한점 그룹 또는 퀴리 제한 그룹이라고 불리는 이 그룹들은 그들을 처음 조사한 피에르 퀴리의 이름을 따서 명명되었다.^[1]^[2] 무한 7개의 축계열은 5개의 제한군(이 중 2개는 중복군)으로 이어지고, 나머지 7개의 점계열은 2개의 연속군(연속군)을 더 생산한다. 국제 표기법에서 표기는 2, ,2, m/m, ,mm, mm/mm, m and, mmm이다.^[3]

유한등분군

원점을 고정된 상태로 두는 3D의 대칭은 원점을 중심으로 한 구체에 대칭이 있는 것이 특징이다. 유한 3D 점 그룹의 경우 구형 대칭 그룹을 참조하십시오.

유한한 3D 지점 그룹의 집합을 결합하기 위해 다음과 같이 구성된다.

2배 이상의 회전 축을 가진 7개의 무한 시리즈; 그것들은 무한 실린더의 유한 대칭 그룹 또는 동등하게 유한 실린더의 유한 대칭 그룹이다. 축점 또는 프리즘 점군이라고도 한다.
3배 이상 회전 축이 여러 개 있는 7개 점 그룹. 3배 이상 회전 축이 7개 모두 포함되기 때문에 3배 이상 회전 축이 여러 개 있는 점 그룹으로 특징지어질 수 있다. 3배 이상 회전 축과 관련하여 가능한 조합은 다음과 같다.
- 3배 축 4개
- 3배 축 4개, 4배 축 3개
- 3배 축 10개, 5배 축 6개

결정학적 제한 정리에 따르면, 제한된 수의 점 그룹은 이산적 변환 대칭과 호환된다: 무한 시리즈 7개에서 27개, 기타 7개 중 5개. 이 두 그룹이 모두 32개의 소위 결정학적 점 그룹을 이룬다.

축 그룹의 무한 7개 시리즈

축 또는 프리즘 그룹의 무한 계열은 지수 n을 가지며, 이것은 어떤 정수일 수 있다. 각 계열에서, n번째 대칭 그룹은 축에 대한 n-폴드 회전 대칭, 즉 360°/n의 회전에 대한 대칭을 포함한다. n=1은 회전 대칭이 전혀 없는 경우를 다룬다. 회전 대칭의 다른 축이 없는 4개의 시리즈(순환 대칭 참조)와 2배 대칭의 추가 축이 있는 3개의 시리즈(이면 대칭 참조)가 있다. 그들은 축 좌표와 그 안에 반사된 반사로 확장된 2차원의 점 그룹으로 이해할 수 있다. 그것들은 프리제 그룹과 관련이 있다;^[4] 그것들은 실린더 주위에서 n번 반복된 프리제 그룹 패턴으로 해석될 수 있다.

다음 표에는 점 그룹에 대한 몇 가지 공식이 나열되어 있다. 헤르만-마우갱 표기법(결정학에서 사용), 쇤파리 표기법(분자 대칭을 설명하는 데 사용), 오비폴드 표기법, 콕세터 표기법. 후자의 세 가지는 그 성질뿐만 아니라, 집단의 질서와도 편리하게 관련되어 있다. 오비폴드 표기법은 통일된 표기법으로 벽지 그룹과 프리제 그룹에도 적용된다. 결정학적 집단은 1, 2, 3, 4, 6으로 제한된다. 결정학적 제약을 제거하면 모든 양의 정수가 가능하다. 시리즈는 다음과 같다.

인틀		쇤파리	오비폴드	콕섹터	프리제	구조적인.	주문	예	평.
even n	홀수 n	쇤파리	오비폴드	콕섹터	(iii)	구조적인.	주문	예	평.
n		C_n	nn	[n]⁺	p1	Z_n	n		n-폴드 회전 대칭
2n	n	S_2n	n×	[2n⁺,2⁺]	p11g	Z_2n	2n		2n배 회전 대칭
n/m	2n	C_nh	n*	[n⁺,2]	p11m	Z_n×Z₂	2n
nmm	nm	C_nv	*nn	[n]	p1m1	디흐_n	2n		피라미드 대칭 생물학에서, 쌍생대칭에서.
n22	n2	D_n	22n	[n,2]⁺	p211	디흐_n	2n		치측 대칭
2n2m	nm	D_nd	2*n	[2n,2⁺]	p2mg	디흐_2n	4n		반격 대칭
n/dv	2n2m	D_nh	*22n	[n,2]	p2mm	디흐_n×Z₂	4n		프리즘 대칭

홀수 n의 경우 Z_2n = Z_n × Z와₂ Dih_2n = Dih_n × Z가₂ 있다.

그룹 C_n(사소한 C₁ 포함)와 D는_n 키랄이고, 나머지는 아킬랄이다.

수평(h)과 수직(v)이라는 용어와 해당 첨자는 회전 축(수직)에 평행하거나 회전 축(수평)에 수직일 수 있는 추가 미러 평면을 가리킨다.

가장 단순한 비특수 축 그룹은 추상 그룹 Z와₂ 동일하다.

C_i(S와₂ 동일) – 반전 대칭
C₂ – 2배 회전 대칭
C_s(Cand_1h C와_1v 동일) – 반사 대칭(양측 대칭이라고도 함)

원통형 밴드의 패턴은 점 그룹의 7개 무한 패밀리 각각에 대한 사례 n = 6을 나타낸다. 각 패턴의 대칭 그룹은 표시된 그룹이다.

이 중 두 번째는 360°/n 각도를 한 바퀴 돌리면 생성되는 순서 n의 단축 그룹(순환 그룹) C(2D에서도 적용 가능) 중_n 첫 번째다. 이 외에도 거울 평면을 축에 수직으로 추가하여 그룹 C에_nh 순서 2n을 부여하거나, 축을 포함하는 n 미러 평면의 집합을 추가하여 그룹 C에_nv 순서 2n을 부여할 수 있다. 후자는 일반적인 n면 피라미드의 대칭군이다. 대칭군 C나_n D를_n 가진 대표적인 물체는 프로펠러다.

수평 반사면과 수직 반사면이 모두 추가되면 이들의 교차로에는 180°까지 n축의 회전축이 주어지기 때문에 그룹이 더 이상 단축이 아니다. 이 새로운 주문 4n 그룹은 D라고_nh 불린다. 그것의 회전 부분군은 순서 2n의 이면군 D로_n, 여전히 1차 회전 축에 수직으로 2배 회전 축을 가지고 있지만 거울 평면은 없다.

참고: 2D에서 D는_n 반사를 포함하는데, 이는 앞면과 뒷면을 구분하지 않고 평평한 물체를 뒤집는 것으로도 볼 수 있지만, 3D에서는 두 가지 작업을 구분한다: D는_n 반사가 아닌 "플립 오버"를 포함한다.

이_nd 계열에는 D(또는 D_nv)라고 불리는 그룹이 하나 더 있는데, 이 그룹은 주 회전축을 포함하는 수직 거울 평면을 가지고 있지만 수평 거울 평면을 갖는 대신 수평면의 반사각과 180°/n 각도로 회전하는 것을 결합한 등위계를 가지고 있다. D는_nh "정규" n-곤 프리즘과 "정규" n-곤 bipyramid의 대칭군이다. D는_nd "일반적인" n-곤 항정신병증 및 "일반적인" n-곤 사다리꼴의 대칭군이다. D는_n 부분 회전("뒤틀린") 프리즘의 대칭군이다.

그룹₂ D와 D는_2h 특별한 회전축이 없다는 점에서 주목할 만하다. 오히려 세 개의 수직 2배 축이 있다. D는₂ 모든 다면 대칭의 부분군(아래 참조_2h), D는 다면군 T와_h O의_h 부분군이다. D는₂ 트위스타인과 같은 분자와 콘카나발린 A와 같은 호모테트라머에서 발생한다. D의₂ 원소는 유닛 립슈비츠 쿼터니온스가 부여한 회전과 1대2로 일치한다.

그룹 S는_n 수평면의 반사 및 360°/n 각도에 의한 회전의 조합에 의해 생성된다. n 홀수의 경우 이는 순서가 2n인 C에_nh 의해 별도로 생성된 그룹과 같으므로, S라는_n 표기법이 필요하지 않다. 그러나 n의 경우에도, n의 경우에도, n의 경우에는, 해당 회전을_nd 포함하지 않고 다수의 부적절한 회전을 포함한다.

7개의 무한 계열의 모든 대칭 그룹은 다음과 같은 4쌍의 상호 대칭 그룹을 제외하고 서로 다르다.

C_1h 및 C_1v: 단일 반사가 있는 순서 2 그룹(C_s )
D₁ 및 C₂: 180° 회전 한 번으로 순서 2 그룹
D와_1h C_2v: 평면에 반사되고 해당 평면의 선을 통해 180° 회전하는 순서 4의 그룹
D와_1d C_2h: 평면에 반사되고 해당 평면에 수직인 선을 통해 180° 회전하는 순서 4의 그룹.

S는₂ 단일 반전(C_i )을 갖는 순서 2의 그룹이다.

"평등한"은 우주에서의 결합과 같은 의미로 여기서 의미한다. 이것은 "대수학적 이형성까지"보다 더 강하다. 예를 들어, 첫 번째 의미에서는 순서 2의 다른 그룹이 세 개 있지만, 두 번째 의미에서는 한 개밖에 없다. 마찬가지로, 예: S는_2n Z와_2n 대수적으로 이형성이다.

그룹은 다음과 같이 구성할 수 있다.

C_n. C라는_n 원소에 의해 생성되며, 이는 축을 중심으로 2˚/n 각도에 의한 회전에 해당한다. 원소는 E(정체), C_n, C_n², ..., C이며_nⁿ⁻¹, 회전각 0, 2 2/n, 4π/n, ..., 2(n - 1)π/n에 해당한다.
S_2n. 원소 Cσ에_2n_h 의해 생성되며, 여기서 σ은_h 축 방향의 반사다. 그것의 원소는 Cσ_2n_h, Cσ_2n³_h, ..., Cσ이_2n²ⁿ⁻¹_h 덧붙여진 C의_n 원소들이다.
C_nh. 원소_n C와 반사 σ에_h 의해 생성된다. 그것의 요소들은 그룹 C의_n 요소들로, 요소들 σ_h, Cσ_n_h, Cσ_n²_h, ..., Cσ이_nⁿ⁻¹_h 덧붙였다.
C_nv. 원소 C에_n 의해 생성되며, 축에 수직인 평면의 방향에서_v 반사된다. 그것의 요소들은 그룹 C의_n 요소들로, 요소들 σ_v, Cσ_n_v, Cσ_n²_v, ..., Cσ이_nⁿ⁻¹_v 덧붙였다.
D_n. 원소_n C와 180° 회전 U = 축에 수직인 평면의 방향을 중심으로 생성된다_h_v. 그것의 요소들은 그룹_n C의 요소들로, 요소 U, CU_n, CU_n², ..., CU가_n^{n − 1} 추가되었다.
D_nd. 원소 Cσ과_2n_h σ에_v 의해 생성된다. 그것의 요소들은 그룹_n C의 요소들과_2n S와_nv C의 추가 요소들이며, 요소들은 Cσσ_2n_h_v, Cσσ_2n³_h_v, ..., Cσσ이_2n^{2n − 1}_h_v 덧붙였다.
D_nh. 원소_n C_h, and, σ에_v 의해 생성된다. 그것의 요소는 그룹 C의_n 요소와 C, C_nv, D의_nh_n 추가 요소들이다.

n ~ ∞을 선택하면 연속 축 회전으로 그룹이 생성된다.

H-M	쇤플라이스	오비폴드	콕시터	한계	추상군
∞	C_∞	∞∞	[∞]⁺	C_n	Z_∞	SO(2)
∞, ∞/m	C_∞	∞*	[2,∞⁺]	C_nh, S_2n	Z₂×Z_∞	Z₂×SO(2)
∞m	C_∞v	*∞∞	[∞]	C_nv	디흐_∞	O(2)
∞2	D_∞	22∞	[2,∞]⁺	D_n	디흐_∞	O(2)
∞m, ∞/mm	D_∞	*22∞	[2,∞]	D_nh, D_nd	Z₂×Dih_∞	Z₂×O(2)

나머지 7개 포인트 그룹

나머지 점군은 순서가 2보다 큰 둘 이상의 회전 축을 가지기 때문에 매우 높은 대칭 또는 다면 대칭이라고 한다. 여기서 C는_n 360°/n을 통한 회전의 축을 나타내고 S는_n 같은 것을 통한 부적절한 회전의 축을 나타낸다. 연속 선에는 오비폴드 표기법, 콕시터 표기법 및 콕시터 도표, 헤르만-마우구인 표기법(완전하고 다르면 약칭), 대칭군 순서(원소 수)가 있다. 그룹은 다음과 같다.

T, (332) [3,3]⁺ () 23 12를 주문하다	치랄 사면 대칭	사면체의 3배 회전 축(C₃) 사면체의 2배 회전 축(C₂) 각 C축은₃ 4개의 C축으로 되어 있는데, 각 C축은 원추형 입방체(이미지의 빨간색 입방체)의 정점 2개를 통과하거나 일반 4면체의 정점 1개를 통과하며, 3개의 C축이₂ 정육면체 면의 중앙 또는 사면체 가장자리의 중간점을 통과한다. 이 그룹은 4개 원소의 교대 그룹인 A와₄ 이형이며, 일반 사면체의 회전 그룹이다. T_d, T, 팔면_h 대칭의 정상 부분군이다. 그룹의 원소는 24단위 허위츠 쿼터니온("이진 사면체 그룹")이 부여한 회전에 1대 2로 대응한다.
T_d, (*332) [3,3] () 43m 주문 24	완전 사면 대칭	사면체의 거울 평면. 사면체의 4배 회전반사축(S₄)이다. 이 그룹은 일반 사면체의 대칭군이다. 이 그룹은 T와 동일한 회전축을 가지고 있으며, C축은₂ 현재 S축이다₄. 이 그룹은 6개의 미러 평면을 가지고 있으며, 각각 큐브의 두 가장자리 또는 4면체의 한 가장자리, 단일 S축₄ 및 2개의 C축을₃ 포함하고 있다. T는_d 4글자의 대칭군인 S에₄ 대해 이형성이 있는데, 이는 T의_d 요소와 4개의 3배 축의 24개 순열 사이에 1 대 1의 일치성이 있기 때문이다. 3배 축 중 하나에 따른_3v C 대칭의 물체는 그러한 4개의 물체로 구성된 궤도에 T의_d 작용에 따라 상승하며, T는_d 이 4개의 물체의 순열 집합에 해당한다. T는_d O의_h 정상 부분군이다. 일반 사면체의 등위계를 참조하십시오.
T_h, (3*2) [3⁺,4] () 2/m3, m3 주문 24	열면 대칭	배구의 솔기는 T 대칭이다_h. 이 그룹은 T와 동일한 회전 축을 가지며, 거울 평면이 큐브 면과 평행하다. C축은₃ S축이₆ 되고, 반전 대칭이 있다. T는_h A₄ × Z에₂ 이형이며(T와 C는_i 모두 정상 부분군이기 때문에), 대칭군₄ S에 대해서는 이형이다. 그것은 인접한 면의 선 세그먼트가 가장자리에서 만나지 않도록 각 면에 선 세그먼트를 두 개의 동일한 직사각형으로 나눈 입방체의 대칭이다. 대칭은 신체 대각선의 고른 순열에 해당하며, 같은 순열과 역순을 결합한다. 또한 각 직사각형이 하나의 대칭축과 4개의 동일한 면과 1개의 다른 면(입방체의 얼굴을 나누는 선 세그먼트에 해당하는 면)을 가진 펜타곤으로 대체되어 설명된 큐브와 유사한 피리토헤드론의 대칭이다. 즉, 큐브의 얼굴이 분할선에서 튀어나와 거기서 좁아진다. 3배 축 10개 중 4개가 있는 완전한 이도사 대칭군(추상군으로서가 아니라 등측군으로서)의 부분군(일반적인 부분군은 아님)이다. O의_h 정상적인 부분군이다. T라고_h 불리지만 사면체에는 적용되지 않는다.
O, (432년) [4,3]⁺ () 432 주문 24	치알 팔면 대칭	이 그룹은 T와 같으나, C₂ 축은 현재₄ C 축이 되며, 추가로 큐브₂ 가장자리의 중간점을 통과하는 6개의 C 축이 있다. 또한 이 그룹은 T와 마찬가지로 3배 축의 24개 순열과 1대 1로 일치하기 때문에 S와₄ 이형성이 있다. 3배 축 중 하나에 따른 D₃ 대칭의 물체는 그러한 4개의 물체로 구성된 궤도에 O의 작용에 따라 상승하며, O는 이들 4개의 물체의 순열 집합에 해당한다. 큐브와 팔면체의 회전군이다. quaternion으로 회전을 나타내는 O는 24단위 Hurwitz 쿼터니온과 24단위 Norm 2의 Lipschitz 쿼터니온으로 이루어져 ${\sqrt {2}}$ , 2 ${\$ 로 나누어 정규화된다 ${\sqrt {2}}$ 이전과 같이 1대 2의 대응이다.
O_h, (*432) [4,3] () 4/m32/m, m3m 주문 48	완전 팔면 대칭	이 그룹은 O와 동일한 회전 축을 가지지만 T와_d T의_h 미러 평면을 모두 구성하는 미러 평면을 가지고 있다. 이_i 그룹은 (O와 C가₂ 모두 정상 부분군이기 때문에) S₄ × Z에 이형이며, 큐브와 팔면체의 대칭 그룹이다. 큐브의 등각도를 참조하십시오.
I, (532) [5,3]⁺ () 532 60을 주문하다	치랄 이두상 대칭	이도사면체와 도두면체의 회전군 대칭 I의_h 전체 그룹에 있는 지수 2의 정규 부분군이다. 이 그룹에는 10가지 버전의₃ D와 6가지 버전의₅ D(프리즘과 반격과 같은 회전 대칭)가 포함되어 있다. 또한 5가지 버전의 T를 포함하고 있다. (5개의 4면체 화합물 참조) 그룹 I는 그 원소가 5개의 T 대칭의 짝수 순열(또는 방금 언급한 5개의 4차 대칭)과 1대 1로 일치하기 때문에 5글자의 교대 그룹인 A에₅ 이형적이다. 회전을 쿼터니온으로 표현하면서 나는 120단위 아이코시안으로 구성되어 있다. 이전과 마찬가지로, 이것은 1 대 2의 통신이다.
I_h, (*532) [5,3] () 532/m, 53m 120을 주문하다	완전한 동면 대칭	이도사면체와 도두면체의 대칭군 그룹 I는_h I와 C가_i 모두 정상 서브그룹이기 때문에 A₅ × Z와₂ 이형성이 있다. 그룹에는 10가지 버전의 D_3d, 6가지 버전의 D_5d(대칭성 대칭성 대칭성 대칭성) 및 5가지 버전의 T가_h 있다.

이러한 그룹과 관련된 연속적인 그룹은 다음과 같다.

∞∞, K 또는 SO(3), 모든 가능한 회전.
∞mm, K_h 또는 O(3), 모든 가능한 회전 및 반사.

무한 등위계 그룹에 대해 위에서 지적했듯이, K 대칭이 있는 모든 물리적 물체는_h K 대칭도 가질 것이다.

반사 콕시터 그룹

3D Coxeter 그룹의 기본 도메인
A₃, [3,3]	B₃, [4,3]	H₃, [5,3]
거울 6개	거울 3+6개	거울 15개
2A₁, [1,2]	3A₁, [2,2]	AA₁₂, [2,3]
거울 2개	거울 3개	거울 4개
A₁, [1]	2A₁, [2]	A₂, [3]
거울 1개	거울 2개	거울 3개

3차원의 반사점 그룹은 Coxeter 그룹이라고도 하며 Coxeter-Dynkin 도표에 의해 주어질 수 있으며 하나의 중앙점에서 교차하는 거울 집합을 나타낸다. Coxeter 표기법은 Coxeter 다이어그램에 해당하는 기호를 제공하며, 회전 및 기타 하위 대칭 점 그룹을 위한 마크업 기호가 있다. 쇤파리 표기법에서 3D의 반사점군은 C_nv, D_nh, 전체 다면군 T, O, I이다.

거울 평면은 구면 표면에 구면 삼각형 도메인 세트를 묶었다. 순위 n Coxeter 그룹은 미러 평면이 n개 있다. 발전기가 3개 미만인 콕시터 그룹은 LUN 또는 반구처럼 퇴보된 구면 삼각형 영역을 가지고 있다. Coxeter 표기법에서 이러한 그룹은 사면 대칭[3,3], 팔면 대칭[4,3], 동면 대칭[5,3], 이면 대칭[p,2]이다. 불가해한 그룹에 대한 미러 수는 nh/2이며 여기서 h는 Coxeter 그룹의 Coxeter 번호, n은 치수(3)이다.^[5]

바일 무리를 짓다		주문	콕시터 번호를 붙이다 (h)	거울 (m)
다면군
A₃	[3,3]	24	4	6
B₃	[4,3]	48	6	3+6
H₃	[5,3]	120	10	15
디헤드랄군
2A₁	[1,2]	4		1+1
3A₁	[2,2]	8		2+1
I₂(p)A₁	[p,2]	4p		p+1
순환군
2A₁	[2]	4		2
아이₂(p)	[p]	2p		p
싱글 미러
A₁	[ ]	2		1

회전 그룹

회전 그룹, 즉 SO(3)의 유한 부분군은 순환 그룹 C_n(정규적 피라미드의 회전 그룹), 이면 그룹_n D(정규적 프리즘 또는 정합적 바이피라미드의 회전 그룹), 그리고 정규 사면체, 팔면체/관, 이코사면체/도면체 그룹의 회전 그룹 T, O, I이다.

특히 D₃, D₄ 등은 3차원 공간에 내장되어 있는 평면 일반 다각형의 회전군이며, 이러한 수치는 퇴행성 정규 프리즘으로 볼 수 있다. 따라서 다이헤드론(그리스어: 두 개의 얼굴을 가진 고체)이라고도 하는데, 디헤드론 그룹이라는 이름이 설명된다.

대칭 그룹 C_n, C_nh, C_nv 또는 S를_2n 가진 물체는 회전 그룹 C를_n 가지고 있다.
대칭 그룹 D_n, D_nh 또는 D를_nd 가진 물체는 회전 그룹 D를_n 가지고 있다.
다면 대칭(T, T, T_d_h, O, O_h, I 또는_h I)을 갖는 물체는 T, O 또는 I라는 첨자가 없는 해당 대칭을 회전 그룹으로 한다.

물체의 회전 그룹은 물체가 키랄인 경우에만 전체 대칭 그룹과 동일하다. 즉, 키랄 물체는 회전 그룹 목록에 대칭 그룹이 있는 물체들이다.

숄나리 표기법, 콕시터 표기법, (orbifold 표기법)에서 주어진 회전 부분군은 다음과 같다.

반사	반사/회전	부적절한 회전	회전
C_nv, [n], (*nn)	C_nh, [n⁺,2], (n*)	S_2n, [2n⁺,2⁺], (n×)	C_n, [n]⁺, (nn)
D_nh, [2,n], (*n22)	D_nd, [2⁺,2n], (2*n)		D_n, [2,n]⁺, (n22)
T_d, [3,3], (*332)			T, [3,3]⁺, (332)
O_h, [4,3], (*432)	T_h, [3⁺,4], (3*2)		O, [4,3]⁺, (432)
I_h, [5,3], (*532)			I, [5,3]⁺, (532)

회전 그룹과 다른 그룹 간의 대응

다음 그룹은 역전을 포함한다.

짝수 n에 대한 C와_nh_nh D
홀수 n에 대한_2n S 및 D_nd(S₂ = C는_i 역전에 의해 생성된 그룹, D_2h = C_1d)
T_h_h_h, O, 나

위에서 설명한 바와 같이, 이들 그룹과 모든 회전 그룹 사이에는 1 대 1의 일치성이 있다.

짝수 n에 대한_nh C와 홀수 n에 대한 S는_2n C에_n 해당한다.
짝수 n에 대한 D와_nh 홀수 n에 대한 D는_nd D에_n 해당한다.
T_h, O_h, I는_h 각각 T, O, I에 해당한다.

다른 그룹은 간접 등위계를 포함하지만 반전하지는 않는다.

C_nv
홀수 n의 경우_nh C 및_nh D
짝수 n에 대한 S와_2n_nd D
T_d

이들은 모두 위에서 설명한 바와 같이 H \ L의 등위계를 뒤집어서 H로부터 얻어진다는 점에서 지수 2의 회전군 H와 부분군 L에 해당한다.

C는_n 지수 2의 D의_n 부분군으로 C를 부여한다_nv.
C는_n 지수 2의 C의_2n 부분군으로 홀수 n은 C_nh, 짝수 n은 S를_2n 나타낸다.
D는_n 지수 2의 D의_2n 부분군으로 홀수 n은_nh D, 짝수 n은_nd D를 나타낸다.
T는 지수 2의 O 부분군으로 T를 부여한다_d.

최대 대칭

이산형 점 그룹이 적절한 부분군으로 가지고 있지 않은 속성을 가진 두 개의 이산형 점 그룹이 있다_h: O와_h I. 그들의 가장 큰 공통 부분군은 T이다_h. 두 그룹은 각각 2배 회전 대칭을 4배로 바꾸고 5배 대칭을 추가해 얻는다.

어떤 결정학적_6h 점 그룹도 그것을 적절한 하위 그룹으로 가지고 있지 않은 속성을 가진 두 개의 결정학적 점 그룹이 있다: O와_h D. 그들의 최대 공통 하위 그룹은 방향에 따라 D와_3d D이다_2h.

추상 그룹 유형별로 정렬된 그룹

위에서 설명한 그룹 아래는 추상 그룹 유형별로 배열되어 있다.

3D에서 대칭 그룹이 아닌 가장 작은 추상 그룹은 쿼터니온 그룹(순서 8), Z₃ × Z (순서₃ 9), 다사이클릭 그룹 Dic₃ (순서 12), 순서 16의 14개 그룹 중 10개 그룹이다.

다음 표의 "순서 2 원소 수" 열은 유형₂ C, C의_i_s 총 등계 부분군 수를 나타낸다. 이 총수는 다양한 추상 그룹 유형을 구별하는 데 도움이 되는 특징 중 하나이며, 등분법 유형은 동일한 추상 그룹의 다양한 등분법 그룹을 구별하는 데 도움이 된다.

3D의 등위계 집단의 가능성 내에는 순서 2의 0, 1, 3 원소를 가진 추상집단 유형이 무한히 많고, 순서 2의 4n + 1 원소를 가진 2개, 순서 2의 4n + 3 원소를 가진 3개(각 n ≥ 8)가 있다. 순서 2의 요소에는 절대 짝수 수가 없다.

추상 그룹으로 순환되는 3D 대칭 그룹

n-폴드 회전 대칭에 대한 대칭 그룹은_n C이며, 추상 그룹 유형은 주기 그룹 Z로_n, C로도 표기된다_n. 그러나 이러한 추상 그룹 유형을 가진 대칭 그룹의 무한 계열은 두 가지 더 있다.

짝수 2n의 경우 축에 수직인 평면에서의 반사와 결합하여 축에 대하여 180°/n 각도로 회전함으로써 생성되는 그룹 S_2n(Chenipples 표기법)가 있다. S의₂ 경우 표기법 C가_i 사용되며, 반대로 생성된다.
n이 홀수인 주문 2n에 대해, 우리는 C를_nh 가지고 있다; 그것은 n-폴드 회전 축과 수직 반사면을 가지고 있다. 축에 대하여 360°/n 각도로 회전하여 반사와 결합하여 생성된다. C의_1h 경우 표기법 C가_s 사용되며, 평면에 반사되어 생성된다.

따라서 10개의 순환 결정점 그룹을 굵게 표시하여 결정학적 제한이 적용된다.

주문	등축군	추상군	순서 2요소수
1	C₁	Z₁	0
2	C₂, C_i, C_s	Z₂	1
3	C₃	Z₃	0
4	C₄, S₄	Z₄	1
5	C₅	Z₅	0
6	C₆, S₆, C_3h	Z₆ = Z₃ × Z₂	1
7	C₇	Z₇	0
8	C₈, S₈	Z₈	1
9	C₉	Z₉	0
10	C₁₀, S₁₀, C_5h	Z₁₀ = Z₅ × Z₂	1

등

추상 그룹으로 분리한 3D 대칭 그룹

2D dihedral 그룹_n D에서 반사는 전면과 후면의 구별 없이 평평한 물체를 뒤집는 것으로도 볼 수 있다.

단, 3D에서는 두 연산이 구별된다. D가_n 나타내는 대칭군은 반사가 아닌 n-폴드 축에 수직인 n개의 2-폴드 축을 포함한다. D는_n 정규 베이스가 있는 n측 프리즘과 정규 베이스가 있는 n측 비피라미드의 회전군이며, 또한 정규적인 n측 반격과 정규적인 n측 사다리꼴의 회전군이다. 또한 그룹은 모든 얼굴에 동일한 치랄 표시를 하거나 모양을 변형하여 키랄을 만든 후 그러한 개체의 전체 대칭 그룹이다.

추상집단형은 dihedral group Dih로_n, D로도_n 표기된다. 그러나 이러한 추상적 그룹 유형을 가진 대칭 그룹의 무한 시리즈는 다음과 같이 세 가지가 더 있다.

순서_nv 2n의 C, 규칙적인 단면 피라미드의 대칭군
순서_nd 4n의 D, 규칙적인 n측 항정신병증의 대칭군
홀수 n의 경우 순서_nh 4n의 D. n = 1의 경우 위에서 이미 설명한 D를₂ 얻게 되므로 n n 3이 된다.

다음 속성을 참고하십시오.

Dih_4n+2

\cong

\cong

Dih

\cong

_2n+1₂ × Z

따라서 12개의 결정학적 점 그룹을 굵게 표시하고 D를_1d 등가 C로_2h 작성한다.

주문	등축군	추상군	순서 2요소수
4	D₂, C_2v, C_2h	Dih₂ = Z₂ × Z₂	3
6	D₃, C_3v	디흐₃	3
8	D₄, C_4v, D_2d	디흐₄	5
10	D₅, C_5v	디흐₅	5
12	D₆, C_6v, D_3d, D_3h	Dih₆ = Dih₃ × Z₂	7
14	D₇, C_7v	디흐₇	7
16	D₈, C_8v, D_4d	디흐₈	9
18	D₉, C_9v	디흐₉	9
20	D₁₀, C_10v, D_5h, D_5d	Dih₁₀ = D₅ × Z₂	11

등

기타

순서 4n의 C는_2n,h 추상 그룹 타입 Z_2n × Z이다₂. n = 1의 경우, 위에서 이미 다룬 Dih를₂ 얻으므로, n 2 2가 된다.

따라서 두 개의 순환 결정점 그룹을 볼드체로 하여 다음과 같이 한다.

주문	등측위군	추상군	순서 2요소수
8	C_4시간	Z₄ × Z₂	3
12	C_6시간	Z₆ × Z₂ = Z₃ × Z₂² = Z₃ × Dih₂	3
16	C_8시간	Z₈ × Z₂	3
20	C_10시간	Z₁₀ × Z₂ = Z₅ × Z₂² = Z₅ × Dih₂	3

등

순서 4n의 D는_nh 추상 그룹 타입 Dih_n × Z이다₂. 홀수 n의 경우 이것은 이미 위에서 다루어졌기 때문에, 우리는 여기에 8n의 D를_2nh 가지고 있는데, 이것은 추상 그룹 타입 Dih_2n × Z (n₂≥1)이다.

따라서 우리는 세 개의 이음 결정점 그룹을 대담하게 구성했다.

주문	등측위군	추상군	순서 2요소수
8	D_2시간	Z₂³	7
16	D_4시간	Dih₄ × Z₂	11
24	D_6시간	Dih₆₂ × Z = Dih₃₂² × Z	15
32	D_8시간	Dih₈ × Z₂	19

등

나머지 7개는 5개의 결정학적 점 그룹(위 참조):

주문	등측위군	추상군	순서 2요소수
12	T	A₄	3
24	T_d, O	S₄	9
24	T_h	A₄ × Z₂	7
48	O_h	S₄ × Z₂	19
60	I	A₅	15
120	I_h	A₅ × Z₂	31

기본 도메인

디디아키스 삼권면체

이두각 대칭에 대한 반사의 평면은 오른쪽 구면 삼각형의 기본 영역과 함께 큰 원의 구를 교차한다.

점 그룹의 기본 영역은 원뿔형 고체다. 주어진 방향에서 주어진 대칭을 가진 물체는 기본영역으로 특징지어진다. 물체가 표면인 경우 그것은 방사형 보르도면이나 표면으로 이어지는 기본 영역의 표면으로 특징지어진다. 표면의 복사본이 맞지 않을 경우 방사형 면이나 표면을 추가할 수 있다. 기본 도메인이 반사 평면에 의해 제한되는 경우 그것들은 어쨌든 적합하다.

다면체의 경우, 기본 영역의 이 표면은 임의 평면의 일부가 될 수 있다. 예를 들어, 이디야키스 삼정면에서는 하나의 완전한 얼굴이 고드름 대칭의 기본 영역이다. 평면의 방향을 조정하면 둘 이상의 인접한 면들을 하나로 결합할 수 있는 다양한 가능성이 주어지며, 같은 대칭을 가진 다양한 다른 다면체를 제공한다. 다면체는 표면이 복사본에 적합하고 평면과 수직인 방사선이 기본 영역에 있는 경우 볼록하다.

또한 기본 영역의 표면은 다중 면으로 구성될 수 있다.

이항 다면 그룹

지도 Spin(3) → SO(3)는 3차원 스핀 그룹에 의한 회전 그룹의 더블 커버로, (Spin(3)이 단순하게 연결되어 있기 때문에 SO(3)의 유일한 연결 커버로 되어 있다.) 격자 정리에는 스핀(3)의 하위 그룹과 SO(3)(회전점 그룹)의 하위 그룹 사이에 갈루아 연결이 있다: 스핀(3)의 하위 그룹의 이미지는 회전점 그룹이고, 포인트 그룹의 프리이미지는 스핀(3)의 하위 그룹이다. (참고) 스핀(3)은 특수 단일 그룹 SU(2)로 대체 설명을 가지고 있으며, 다음과 같다. 단위 쿼터니온의 무리 지형학적으로 이 Lie 그룹은 3차원 구체 S³.)

유한점군의 프리이미지를 binaryl,n,m⟩로 나타내는 2진 다면체군이라고 하며, 접두사 2진법으로 점군(l,m,n)과 같은 이름으로 부름하며, 관련 다면군(l,m,n)의 순서가 두 배가 된다. 예를 들어, 이도사면군(2,3,5)의 전상은 2진수 이도사면군(2,3,5)이다.

이항 다면 그룹은 다음과 같다.

$A_{n}$ n ${\$ : a (n + 1)-곤의 이진 주기 그룹, 순서 2n
$D_{n}$ $D_{n}$ ${\$ : n곤의 바이너리 다이헤드 그룹, n2,n⟩, order 4n
$E_{6}$ $E_{6}$ ${\$ : 이진 사면군, group2,3,33, 주문 24
$E_{7}$ $E_{7}$ ${\$ : 바이너리 옥타헤드 그룹, ⟨2,3,4⟩, 주문 48
$E_{8}$ $E_{8}$ ${\$ : 바이너리 이코사시드 그룹, 2,3,53, 주문 120

이것들은 ADE 분류에 의해 분류되며, 이항 다면체의 작용에 의한 C의² 몫은 두발 특이점이다.^[6]

방향을 역방향으로 하는 포인트 그룹의 경우 핀 그룹이 두 개여서 주어진 포인트 그룹에 해당하는 이진 그룹이 두 개 있을 수 있어 상황이 더 복잡하다.

이것은 그룹의 덮개이지 공간의 덮개가 아니라는 점에 유의하십시오. 구는 단순히 연결되어 있으므로 덮개 공간이 없다. 따라서 3차원 다면체를 덮고 있는 "이중 다면체"라는 개념은 존재하지 않는다. 이진 다면 그룹은 스핀 그룹의 이산 하위 그룹이며, 스핀 그룹의 표현에 따라 벡터 공간에 작용하며, 이 표현에서 다면체는 안정화될 수 있다 - 지도 Spin(3) → SO(3)에 따르면 스핀 표현 또는 기타 대표에 있는 동안 기본 (비이항) 그룹이 작용하는 것과 동일한 다면체에 작용한다.다른 다면체를 안정시킬 수 있는 양.

이것은 투사적인 다면체와는 대조적이다 – 구는 투사적인 공간(그리고 렌즈 공간도 포함)을 포괄하고, 따라서 투사적인 공간이나 렌즈 공간의 테셀레이션은 다면체의 뚜렷한 개념을 산출한다.

참고 항목

각주

^ Curie, Pierre (1894). "Sur la symétrie dans les phénomènes physiques, symétrie d'un champ électrique et d'un champ magnétique" [On symmetry in physical phenomena, symmetry of an electric field and a magnetic field] (PDF). Journal de Physique (in French). 3 (1): 393–415. doi:10.1051/jphystap:018940030039300.
^ Shubnikov, A.V. (1988). "On the Works of Pierre Curie on Symmetry". Crystal Symmetries: Shubnikov Centennial papers. Pergamon Press. pp. 357–364. doi:10.1016/B978-0-08-037014-9.50007-8. ISBN 0-08-037014-4.
^ Vainshtein., B. K. (1994). Modern Crystallography, Vol. 1. Fundamentals of Crystals. Symmetry, and Methods of Structural Crystallography (2nd enlarged ed.). Springer-Verlag Berlin. p. 93. ISBN 978-3-642-08153-8.
^ Fisher, G.L.; Mellor, B. (2007), "Three-dimensional finite point groups and the symmetry of beaded beads" (PDF), Journal of Mathematics and the Arts, 1 (2): 85–96, doi:10.1080/17513470701416264, S2CID 40755219
^ Coxeter, 일반 폴리토페스', §12.6 반사 횟수, 방정식 12.61
^ Burban, Igor. "Du Val Singularities" (PDF).

참조

Coxeter, H. S. M. (1974), "7 The Binary Polyhedral Groups", Regular Complex Polytopes, Cambridge University Press, pp. 73–82.
Coxeter, H. S. M. & Moser, W. O. J. (1980). Generators and Relations for Discrete Groups, 4th edition. New York: Springer-Verlag. ISBN 0-387-09212-9. 6.5 이항 다면군, 페이지 68
Conway, John Horton; Huson, Daniel H. (2002), "The Orbifold Notation for Two-Dimensional Groups", Structural Chemistry, Springer Netherlands, 13 (3): 247–257, doi:10.1023/A:1015851621002, S2CID 33947139

외부 링크

32개의 결정학적 점 그룹의 그래픽 개요 – 7개의 무한 시리즈 중 첫 번째 부분(n=5)과 7개의 개별 3D 점 그룹 중 5개를 건너뛰지 않음
점 그룹의 속성 개요
각 대칭 유형의 가장 간단한 표준 폴리헤드라(Java 사용)
점 그룹 및 결정 시스템, 이수 웨이, 페이지 4–6
지오메트리 센터: 데카르트 좌표에서의 대칭 공식 10.1(3차원)

[1] Curie, Pierre (1894). "Sur la symétrie dans les phénomènes physiques, symétrie d'un champ électrique et d'un champ magnétique" [On symmetry in physical phenomena, symmetry of an electric field and a magnetic field] (PDF). Journal de Physique (in French). 3 (1): 393–415. doi:10.1051/jphystap:018940030039300.

[2] Shubnikov, A.V. (1988). "On the Works of Pierre Curie on Symmetry". Crystal Symmetries: Shubnikov Centennial papers. Pergamon Press. pp. 357–364. doi:10.1016/B978-0-08-037014-9.50007-8. ISBN 0-08-037014-4.

[3] Vainshtein., B. K. (1994). Modern Crystallography, Vol. 1. Fundamentals of Crystals. Symmetry, and Methods of Structural Crystallography (2nd enlarged ed.). Springer-Verlag Berlin. p. 93. ISBN 978-3-642-08153-8.

[4] Fisher, G.L.; Mellor, B. (2007), "Three-dimensional finite point groups and the symmetry of beaded beads" (PDF), Journal of Mathematics and the Arts, 1 (2): 85–96, doi:10.1080/17513470701416264, S2CID 40755219

[5] Coxeter, 일반 폴리토페스', §12.6 반사 횟수, 방정식 12.61

[6] Burban, Igor. "Du Val Singularities" (PDF).

[1]

[2]

[3]

[4]

[5]

[6]

Search