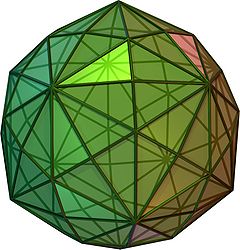
디디아키스 삼권면체

디디아키스 삼권면체
(회전 및 3D 모델)
유형	카탈루냐 주
콘웨이 표기법	mD 또는 dbD
콕시터 다이어그램
면 폴리곤	스칼린 삼각형
얼굴	120
가장자리	180
정점	62 = 12 + 20 + 30
면 구성	V4.6.10
대칭군	Ih, H3, [5,3], (*532)
회전군	I, [5,3]+, (532)
디헤드각	164° 53' 17 아르코스(arccos)-179-24√5/241)
이중 다면체	잘린 이코시다데카헤드론
특성.	볼록한, 얼굴-변형
그물을 치다

기하학에서 이디야키스 삼콘체드론, 육각체 이코사헤드론, 데카키스 도데카헤드론 또는 키스롬 삼콘체드론은^[1] 120개의 얼굴을 가진 카탈로니아 고형이며, 아치메드 잘린 이코사데카헤드론에 대한 이중이다. 그만큼 얼굴형은 균일하지만 얼굴 폴리곤이 불규칙하다. 그것은 부풀려진 롬브 삼정삼정삼정삼면체를 약간 닮았다. 즉, 롬브 삼정삼면체의 각 면을 하나의 꼭지점으로 바꾸고, 4개의 삼각형을 규칙적으로 바꾸면, 결국 디스다키 삼정삼면체로 끝난다. 즉, 이디다키스 삼콘타헤드론은 롬브릭 삼콘타헤드론의 클라이토프(Kleetope)이다. 또한 아르키메데스·카탈란 고형물 중 가장 많은 얼굴을 가지고 있으며, 스누브 도데카헤드론은 92면으로 2위를 차지했다.

만약 바이프라임, 교량화 바이프라임, 사다리꼴을 제외한다면, 다면체의 모든 면이 동일한 다른 어떤 엄격히 볼록한 다면체 중 가장 많은 얼굴을 가지고 있다.

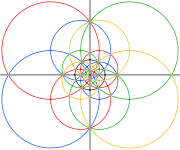
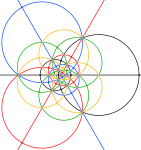
구체에 투영된 디스다키스 삼관면체의 가장자리는 15개의 큰 원을 정의한다. 벅민스터 풀러는 이 15개의 원과 다른 2개의 다른 다면체에 10개, 6개의 원과 함께 구면 이코사면체의 31개의 원들을 정의하기 위해 사용했다.

얼굴

이디야키스 삼권면체의 얼굴은 스칼린 삼각형이다. If ${\displaystyle \phi }$ is the golden ratio then their angles are equal to ${\displaystyle \arccos({\frac {-4\phi +7}{30}})\approx 88.991\,801\,907\,82^{\circ }}$, ${\displaystyle \arccos({\frac {-4\phi +$$17}{20}})\approx 58.237\,919\,620\,89^{\circ }}$ and ${\displaystyle \arccos({\frac {5\phi +2}{12}})\approx 32.770\,278\,471\,29^{\circ }}$.

대칭

구에 투영된 다면체의 가장자리는 15개의 큰 원을 형성하며, 반사 I_h 고면 대칭의 15개의 거울 평면을 모두 나타낸다. 빛과 어두운 삼각형의 쌍을 결합하는 것은 비반사 (I) 이두 대칭의 기본 영역을 정의한다. 5개의 옥타헤드라의 합성물의 가장자리는 또한 동면 대칭의 10개의 거울 평면을 나타낸다.

디디아키스 삼권면체

델토이달 육면체

롬빅 삼권면체

도데카헤드론

이코사헤드론

피리토헤드론

구면 다면체
(회전 모델 참조)	2배, 3배, 5배 축의 직교 투영

입체 투영
	2배	3배	5배
다섯 개의 옥타헤드라를 혼합하여 색칠하였고, 각 옥타헤드론마다 3개의 원형이 있다. 아래 검은 원 안의 면적은 구형 다면체의 전반구에 해당한다.

직교 투영

이디다키스 삼정면에는 직교 투영에서 중심일 수 있는 세 가지 유형의 정점이 있다.

직교 투영

투영적 대칭	[2]	[6]	[10]
이미지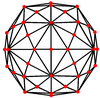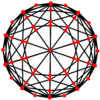
이중 이미지

사용하다

이디다키스 삼정삼면체(disdyakis triacontahedron)는 펜타곤을 각각 10개의 삼각형으로 나눈 일반 도데면체로서 루빅 큐브와 같은 콤비네이션 퍼즐을 위한 '성스러운 그레일'로 여겨진다. 종종 "대단한" 문제라 불리는 이 미해결 문제는 현재 만족스러운 메커니즘을 가지고 있지 않다. 그것은 기계적인 퍼즐에서 가장 중요한 미해결 문제다.^[2]

이 모양은 3D 프린팅으로 d120 주사위를 만들 때 사용되었다.^[3] 다이스랩은 2016년부터 디스다키스 삼정면체를 사용해 사출 성형 120면 다이(Side Side Die)^[4]를 대량 판매하고 있다. d120은 장기간 굴러가는 경향으로 인해 현실적으로 실용적이지 못할 무한가족(바른정규 프리즘, 양다리꼴, 사다리꼴 등)을 제외하고 공정한 주사위에 가장 많은 가능한 얼굴이라는 주장이다.^[5]

구에 투영된 디스다이나키스 트리콘헤드론은 STEM 관련 주제에 대한 일련의 레슨을 담고 있는 웹사이트인 브릴리언트의 로고로 사용된다.^[6]

관련 다면체 및 틸팅

이디야키스 삼콘타헤드론과 유사한 폴리헤드라는 보타이 이코사헤드론과 도데카헤드론에 이중으로 되어 있으며, 추가적인 삼각면 쌍을 포함하고 있다.[7]

균일한 이두면체 다면체 계열
대칭: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
이중에서 균일한 폴리헤드라까지
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

표면학적으로 얼굴 구성 V4.6.2n에 의해 정의된 다면체 시퀀스와 관련이 있다. 이 그룹은 정점당 모든 고른 수의 가장자리를 가지며 평면의 다면선과 무한선을 통해 이등분 평면을 형성하고, n 7 7에 대해 쌍곡면으로 연속하는 데 특별하다.

모든 꼭지점에 균일한 수의 면이 있는 경우, 이러한 다면체와 기울기는 두 가지 색을 교대로 표시하여 인접한 모든 면이 서로 다른 색을 가질 수 있다.

또한 이러한 영역의 각 면은 각 삼각형 면 정점에 2,3,n 미러 순서가 있는 대칭 그룹의 기본 영역에 해당한다. 이것은 Orbifold 표기법으로 *n32이고, Coxeter 표기법으로 [n,3]이다.

*n32 전분해 틸팅의 대칭 변이: 4.6.2n v t
Sym. *n32 [n,3]	구면				유클리드	콤팩트 하이퍼브.		파라코.	비대칭 쌍곡선
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
수치
구성.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
듀얼스
구성.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.1987	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

참조

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3-9)절)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (13반경 볼록 다면체 및 그 이중체 25페이지 디스다이아키스트리아콘타면체)
• 2008년 사물의 대칭, 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, ISBN 978-1-56881-220-5[1] (21장, 아르키메데스 및 카탈란 다면체의 명명 및 기울기, 285페이지 키스롬빅 3면)

외부 링크

• Eric W. Weisstein, Disdyakis triacontahedron (Catalan solid) at MathWorld.
• 디스다키스 삼정삼면체(Hexakis Icosaheadron) – 대화형 다면체 모델