선 그래프

그래프 이론의 수학적 계율에서, 비방향 그래프 G의 선 그래프는 G(G)의 가장자리 사이의 부조화를 나타내는 또 다른 그래프 L(G)이다. G의 각 가장자리에서 L(G)로 정점을 만들고, G의 두 가장자리에서 정점을 공통으로 갖는 가장자리 사이에 엣지를 만든다.s in L(G)

이름 선 그래프는 휘트니(1932년)와 크라우즈(1943)가 모두 이 전에 이 공사를 사용했음에도 불구하고 하라리와 노먼(1960년)의 논문에서 나온 것이다.^[1] 그 밖에 선 그래프에 사용되는 용어로는 피복 그래프, 파생 그래프, 에지-투-베르텍스 이중, 결합 그래프, 대표 그래프, ob-오브라섬과 더불어 에지 그래프, 교환 그래프, 조정 그래프, 파생 그래프 등이 있다.^[1][2]

Hassler Whitney(1932)는 하나의 예외적인 사례로 연결된 그래프 G의 구조가 선 그래프에서 완전히 복구될 수 있다는 것을 증명했다.^[3] 선 그래프의 다른 많은 특성들은 기초 그래프의 속성을 꼭지점에서 가장자리로 번역함으로써 따르며 휘트니의 정리로는 같은 번역도 다른 방향으로 할 수 있다. 선 그래프는 발톱이 없고, 초당적 그래프의 선 그래프는 완벽하다. 선 그래프는 금지된 9개의 하위 그래프로 특징지어지며 선형 시간 내에 인식할 수 있다.

선 그래프의 선 그래프, 다중 그래프의 선 그래프, 하이퍼그래프의 선 그래프, 가중 그래프의 선 그래프 등 선 그래프의 개념에 대한 다양한 확장이 연구되었다.

형식 정의

그래프 G를 지정하면 해당 선 그래프 L(G)은 다음과 같은 그래프다.

• L(G)의 각 꼭지점은 G의 가장자리를 나타낸다.
• L(G)의 두 꼭지점은 해당 가장자리가 G의 공통 끝점("사건")을 공유하는 경우에만 인접한다.

즉, G의 가장자리의 교차 그래프로, 두 끝점의 집합으로 각 가장자리를 나타낸다.^[2]

예

다음 그림은 그래프(왼쪽, 파란색 꼭지점 포함)와 선 그래프(오른쪽, 녹색 꼭지점 포함)를 보여준다. 선 그래프의 각 꼭지점은 원래 그래프에서 해당 에지의 끝점 쌍으로 라벨이 표시되어 있다. 예를 들어, 오른쪽의 녹색 정점은 파란색 정점 1과 3 사이의 왼쪽 가장자리에 해당한다. 녹색 꼭지점 1,3은 1,4 및 1,2(파란색 그래프에서 끝점 1을 공유하는 가장자리와 대응) 및 4,3(파란색 그래프에서 끝점 3을 공유하는 가장자리와 대응)의 다른 세 가지 녹색 꼭지점에 인접한다.

• 

  그래프 G

• 

  L(G)의 정점이 G의 가장자리에서 생성됨

• 

  L(G)에 모서리 추가

• 

  선 그래프 L(G)

특성.

기본 그래프의 변환된 속성

가장자리 사이의 인접성에만 의존하는 그래프 G의 속성은 꼭지점 사이의 인접성에 의존하는 L(G)의 등가 속성으로 변환될 수 있다. 예를 들어, G의 일치는 둘 중 어느 쪽도 인접하지 않는 가장자리 집합이며, 둘 중 어느 쪽도 인접하지 않는 L(G)의 정점 집합, 즉 독립 집합에 해당한다.^[4]

그러므로,

• 연결된 그래프의 선 그래프가 연결되어 있다. G가 연결되면 가장자리 두 개 중 어느 하나를 연결하는 경로를 포함하는데, 이는 L(G)의 정점 두 개를 포함하는 L(G)의 경로로 해석된다. 그러나 일부 분리된 정점을 가지고 있고 따라서 연결이 끊긴 그래프 G는 그럼에도 불구하고 연결된 선 그래프를 가질 수 있다.^[5]
• 선 그래프는 기초 그래프에 어느 끝점도 1도가 없는 브리지가 있는 경우에만 굴절점을 가진다.^[2]
• 정점과 m 가장자리가 n개인 그래프 G의 경우 선 그래프 L(G)의 정점 수는 m이고, L(G)의 정점 수는 G의 정점 도 제곱합(-m)의 절반이다.^[6]
• L(G)의 독립 집합은 G의 일치에 해당한다. 특히 L(G)의 최대 독립 집합은 G의 최대 일치에 해당한다. 최대 일치 집합은 다항 시간에서 찾을 수 있으므로, 더 일반적인 그래프 패밀리의 최대 독립 집합 문제의 경도에도 불구하고 선 그래프의 최대 독립 집합도 찾을 수 있다.^[4] 마찬가지로 L(G)에 있는 무지개 독립 집합은 G에 있는 무지개 일치에 해당한다.
• 그래프 G의 에지 색도 번호는 선 그래프 L(G)의 정점 색도와 같다.^[7]
• 에지 변환 그래프의 선 그래프는 정점 변환이다. 이 속성은 (피터슨 그래프와 마찬가지로) 정점 변환이지만 Cayley 그래프가 아닌 그래프의 패밀리를 생성하는 데 사용될 수 있다: G가 정점 5개 이상이고, 양립하지 않으며, 정점도가 홀수인 경우 L(G)은 정점 변환 비 Cayley 그래프다.^[8]
• 그래프 G에 오일러 사이클, 즉 G가 연결되어 있고 각 꼭지점에 짝수 수의 가장자리가 있으면 G의 선 그래프가 해밀턴이다. 그러나 선 그래프의 모든 해밀턴 사이클이 이런 식으로 오일러 사이클에서 오는 것은 아니다. 예를 들어, 해밀턴 그래프 G의 선 그래프는 G도 오일러 사이클인지에 관계없이 그 자체로 해밀턴 그래프다.^[9]
• 만약 두 개의 단순한 그래프가 이형이라면, 그들의 선 그래프 또한 이형성이다. 휘트니 그래프 이형성 정리는 한 쌍의 그래프를 제외한 모든 그래프에 대해 이와 반대되는 내용을 제공한다.
• 복잡한 네트워크 이론의 맥락에서, 임의 네트워크의 선 그래프는 소세계 속성(정점 쌍들 사이에 짧은 경로의 존재)과 그 정도 분포의 모양과 같은 네트워크의 많은 속성을 보존한다.^[10] Evans & Lambiotte(2009)는 복잡한 네트워크에서 정점 군집을 찾는 모든 방법을 선 그래프에 적용하고 대신 가장자리를 군집화하는 데 사용할 수 있다고 관찰한다.

휘트니 이소모르프 정리

연결된 두 그래프의 선 그래프가 이형인 경우, 삼각형 그래프₃ K와 이형선 그래프는 있지만 그 자체가 이형선 그래프는 아닌 클로 K의_1,3 경우를 제외하고, 기초 그래프는 이형성이다.^[3]

K와₃ K뿐만_1,3 아니라 선 그래프가 그래프 자체보다 대칭도가 높다는 특성을 가진 다른 예외적인 작은 그래프도 있다. 예를 들어, 다이아몬드 그래프_1,1,2 K(가장자리를 공유하는 두 삼각형)는 4개의 그래프 자동화를 가지고 있지만, 선_1,2,2 그래프 K는 8개의 그래프 자동화를 가지고 있다. 표시된 다이아몬드 그래프의 그림에서 그래프를 90도 회전시키는 것은 그래프의 대칭이 아니라 선 그래프의 대칭이다. 그러나 그러한 예외적인 경우는 모두 최대 4개의 꼭지점이 있다. 휘트니 이소모르피즘 정리의 강화된 버전은 정점이 4개 이상인 연결된 그래프의 경우 그래프의 이소모르피즘과 선 그래프의 이소모르피즘 사이에 일대일 일치성이 있다고 명시하고 있다.^[11]

휘트니 이소모르피즘 정리의 유사성은 다문자의 선 그래프에 대해 증명되었지만, 이 경우에는 더욱 복잡하다.^[12]

매우 정규적이고 완벽한 선 그래프

전체 그래프 K의_n 선 그래프는 삼각형 그래프, 존슨 그래프 J(n, 2) 또는 크네저 그래프 KG의_n,2 보완재라고도 한다. 삼각형 그래프는 n = 8을 제외하고 스펙트럼이 특징이다.^[13] 또한 매개변수 srg(n(n - 1)/2, 2(n - 2, n - 2, 4)가 있는 강력한 정규 그래프로 특성화(K 제외)할₈ 수 있다).^[14] L(K₈)과 매개변수와 스펙트럼이 같은 세 개의 강력 정규 그래프는 창 그래프인데, L(K₈)에서 그래프 전환을 통해 얻을 수 있다.

초당적 그래프의 선 그래프는 완벽하지만(Kőnig의 정리 참조), 발톱 그래프의 예처럼 초당적일 필요는 없다. 초당적 그래프의 선 그래프는 완벽한 그래프의 핵심 구성 요소 중 하나를 형성하며, 강력한 완벽한 그래프 정리의 증거에 사용된다.^[15] 이러한 그래프의 특별한 예로는 룩의 그래프, 완전한 양분 그래프의 선 그래프가 있다. 완전한 그래프의 선 그래프와 마찬가지로, 정점 수, 가장자리 수, 인접 지점과 비인접 지점의 공유 인접 지점 수로 하나의 예외를 특징지을 수 있다. 예외적인 경우는 L(K_4,4)으로, 그 파라미터를 슈리칸데 그래프와 공유한다. 초당파의 양쪽이 같은 정점 수를 가질 때, 이 그래프들은 다시 강하게 규칙적이다.^[16]

보다 일반적으로 그래프 G는 L(G)이 완벽한 그래프라면 선 완벽한 그래프라고 한다. 선 완성도 그래프는 정확히 3보다 큰 홀수 길이의 단순한 주기를 포함하지 않는 그래프다.^[17] 동등하게, 그래프도 각각의 2차원 구성요소가 초당적이거나 K형식₄(사면체) 또는_1,1,n K형(하나 이상의 삼각형 모두가 공통의 가장자리를 공유하는 책)일 경우에만 선으로 완벽하다.^[18] 모든 선 완벽한 그래프는 그 자체로 완벽하다.^[19]

기타 관련 그래프 패밀리

모든 선 그래프는 발톱이 없는 그래프, 세 잎 나무 형태의 유도 하위 그래프가 없는 그래프다.^[20] 보다 일반적으로 클로가 없는 그래프의 경우처럼 가장자리 수가 짝수인 모든 연결 선 그래프 L(G)은 완벽하게 일치한다.^[21] 동등하게, 이는 기초 그래프 G에 짝수 수의 가장자리가 있으면 가장자리를 2-엣지 경로로 분할할 수 있다는 것을 의미한다.

나무의 선 그래프는 정확히 발톱이 없는 블록 그래프다.^[22] 이 그래프들은 극한 그래프 이론의 문제를 해결하기 위해 사용되어왔다. 주어진 수의 가장자리와 정점을 가진 그래프를 구성하는데, 가능한 한 서브그래프로 유도된 가장 큰 나무가 작다.^[23]

선 그래프의 인접$$ 행렬 $A{\displaystyle }$ ${\displaystyle A}$의 모든 고유값은 -2 이상이다. 그 이유는 $A{\displaystyle }$ ${\displaystyle A}$을(를) A${\displaystyle }$= ${\displaystyle {J\mathsf{}}^{}}$ ${\displaystyle T^{}}$- 2 ${\displaystyle \mathrm{I}}$ ${\displaystyle A=J^{\mathsf{T}J-2I}$로 쓸 수$$ 있기 때문이며$,$ $여기$서 J ${\displaystyle J}$은 선 그래프의 부호 없는 발생 행렬이고 $I{\displaystyle }$ ${\displaystyle I}$은 정체성이다$$. ${\displaystyle \mathrm{특히}}$ $A{\displaystyle }$+ ${\displaystyle 2}$ I ${\디스플레이$ 스타일 $A+2$$I}$은 벡터 시스템의 Gramian 행렬로, 이 속성을 가진 모든 그래프를 일반화된 선 그래프라고 부른다.^[24]

특성화 및 인식

클라이크 파티션

임의 그래프 G와 임의의 정점 v(G)의 경우, v에 입사하는 가장자리 집합은 선 그래프 L(G)의 클라이크에 해당한다. 이러한 방식으로 형성된 패거리들은 L(G)의 가장자리를 분할한다. L(G)의 각 꼭지점은 정확히 두 개에 속한다(G에서 해당 에지의 두 끝점에 해당하는 두 개의 부류).

이러한 분할 영역은 선 그래프의 특성을 나타내기 위해 사용될 수 있다: 그래프 L은 L의 가장자리를 분할하는 (일부 분할 영역은 정점일 수 있음)에서 분류 집합을 찾을 수 있는 경우에만 L의 각 정점이 정확히 속하도록 L의 가장자리를 분할하는 다른 그래프 또는 다중 그래프의 선 그래프다. 패거리의 ^[20]두 패거리 동일한 두 개의 정점 L이 모두 없다는 추가 조건을 만족하는 경우, 다중 그래프가 아닌 그래프의 선 그래프다. 그러한 패밀리의 계열을 감안할 때, L이 선 그래프인 기초 그래프 G는 각 패밀리에 대해 G에 하나의 꼭지점을 만들고, 그 끝점이 L에 정점을 포함하는 두 개의 패밀리로 L의 각 정점에 대한 가장자리를 만들어 복구할 수 있다. 휘트니의 이형성 정리의 강한 버전에 의해, 기초 그래프 G가 f보다 많은 경우.우리의 정점들, 이 타입의 파티션은 오직 하나일 수 있다.

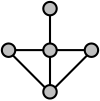
예를 들어, 이 특성화는 다음 그래프가 선 그래프가 아님을 보여주는 데 사용될 수 있다.

이 예에서 중앙도에서 위쪽으로, 왼쪽으로, 오른쪽으로 가는 가장자리-4정점에는 공통적인 구분이 없다. 따라서 그래프 가장자리의 어떤 분할도 이 세 개의 가장자리 각각에 대해 적어도 하나의 클릭을 가져야 하며, 이 세 개의 클릭은 모두 그 중심 꼭지점에서 교차하여 각 꼭지점이 정확히 두 개의 클릭에 나타나야 한다는 요건을 위반하게 된다. 따라서 표시된 그래프는 선 그래프가 아니다.

금지된 하위 그래프

선 그래프의 또 다른 특성화는 비네케(1970년)에서 입증되었다(1968년) 비네케(1968년)의 증거 없이 앞서 보고되었다. 그는 선 그래프가 아닌 모든 그래프가 9개의 최소 그래프를 유도 하위 그래프로 가지고 있다는 것을 보여주었다. 즉, 그래프는 정점의 부분 집합이 이 9개의 그래프 중 하나를 유도하지 않는 경우에만 선 그래프다. 위의 예에서, 가장 위쪽의 꼭지점 4개는 금지된 서브그래프 그림의 왼쪽 상단에 표시된 발톱(즉_1,3, 완전한 양분 그래프 K)을 유도한다. 따라서 베이네케의 특성화에 의해 이 예는 선 그래프가 될 수 없다. 최소 등급이 5 이상인 그래프의 경우, 그림의 왼쪽과 오른쪽 열에 있는 여섯 개의 하위 그래프만 특성화에 필요하다.^[25]

알고리즘

루소풀로스(1973)와 레오트(1974)는 선 그래프를 인식하고 원래 그래프를 재구성하기 위한 선형 시간 알고리즘을 설명했다. Syswo(1982)는 이러한 방법을 지시된 그래프에 일반화했다. Degiorgi & Simon(1995)은 각 단계에서 변경된 가장자리 수에 비례하여 정점 삽입 및 삭제에 따라 동적 그래프를 유지하고 입력의 표현을 선 그래프(존재할 때)로 유지하기 위한 효율적인 데이터 구조를 설명했다.

루소풀로스(1973)와 르호트(1974)의 알고리즘은 홀수 삼각형(홀수 삼각형 정점 근처에 또 다른 정점이 있다는 속성이 있는 선 그래프의 삼각형)을 포함하는 선 그래프의 특성화에 기초한다. 그러나 Degiorgi & Simon(1995)의 알고리즘은 휘트니의 이소모르피즘 정리만을 사용한다. 나머지 그래프를 선 그래프로 만드는 삭제를 인식해야 하기 때문에 복잡하지만 정적 인식 문제에 특화된 경우 삽입만 수행하면 되고 알고리즘은 다음과 같은 단계를 수행한다.

• 각 단계에서 하나 이상의 이전에 추가된 정점에 인접한 정점을 선택하여 정점을 한 번에 하나씩 추가하여 입력 그래프 L을 생성하십시오. L에 정점을 추가하는 동안 L = L(G)에 대한 그래프 G를 유지하십시오. 알고리즘이 적절한 그래프 G를 찾지 못하면 입력이 선 그래프가 아니며 알고리즘이 종료된다.
• G의 정점이 4개 이하인 그래프 L(G)에 정점 v를 추가할 때 선 그래프 표현이 고유하지 않은 경우가 있을 수 있다. 그러나 이 경우 증강 그래프는 충분히 작아서 일정한 시간 내에 짐승의 힘 검색을 통해 선 그래프로 표현될 수 있다.
• 다른 그래프 G의 선 그래프와 같은 큰 그래프 L에 꼭지점 v를 추가할 때, L에서 v의 이웃에 해당하는 가장자리로 형성된 G의 하위 그래프가 S가 되도록 한다. S에 하나의 꼭지점 또는 두 개의 비인접 정점으로 구성된 꼭지점 커버가 있는지 확인하십시오. 커버에 두 개의 정점이 있는 경우 이 두 정점을 연결하는 에지(v에 대응)를 추가하여 G를 증가시킨다. 커버에 꼭지점이 하나만 있으면 이 꼭지점 근처에 있는 G에 새 꼭지점을 추가하십시오.

각 단계에는 일정한 시간이 걸리거나, 크기가 v의 이웃 수에 비례하는 그래프 S 내에서 일정한 크기의 꼭지점 커버를 찾는 작업이 포함된다. 따라서 전체 알고리즘의 총 시간은 (핸드쉐이킹 보조정리) 입력 에지 수에 비례하는 모든 정점의 인접 숫자의 합에 비례한다.

선 그래프 연산자 반복

판 로이 & 윌프(1965)는 그래프의 순서를 고려한다.

${\displaystyle G,L(G),L(L(G)),\dots .\ }$

이들은 G가 유한 연결 그래프일 때 다음 순서에 대해 네 가지 동작만 가능하다는 것을 보여준다.

• G가 사이클 그래프인 경우 L(G)과 이 시퀀스의 각 후속 그래프는 G 자체와 이형성이다. 이것들은 L(G)이 G에 이형성인 유일한 연결된 그래프들이다.^[26]
• G가 집게 K인_1,3 경우 L(G)과 시퀀스의 모든 후속 그래프는 삼각형이다.
• G가 경로 그래프인 경우, 시퀀스의 각 후속 그래프는 더 짧은 경로가 된다. 결국 빈 그래프와 함께 시퀀스가 종료된다.
• 나머지 모든 경우에서, 이 시퀀스의 그래프 크기는 결국 구속 없이 증가한다.

G가 연결되지 않은 경우 이 분류는 G의 각 구성요소에 별도로 적용된다.

경로가 아닌 연결된 그래프의 경우 선 그래프 작업의 모든 반복 횟수가 충분히 높은 경우 해밀턴식 그래프가 생성된다.^[27]

일반화

내적 그래프 및 볼록 다면체

평면 그래프 G가 최대 정점 3을 가질 때, 선 그래프는 평면이며, G의 모든 평면 내장도는 L(G)의 내장까지 확장될 수 있다. 그러나 선 그래프가 평면이 아닌 더 높은 수준의 평면 그래프가 존재한다. 예를 들어, 여기에는 5성_1,5 K, 일반 펜타곤 내에 두 개의 비 교차 대각선을 추가하여 형성된 보석 그래프, 그리고 4도 이상의 정점을 가진 모든 볼록한 다면체 등이 포함된다.^[28]

대체 구성인 내적 그래프는 최대 도 3의 평면 그래프에 대한 선 그래프와 일치하지만 항상 평면형이다. 선 그래프와 정점이 같지만 잠재적으로 가장자리가 적을 수 있다. 두 개의 정점이 평면 내장의 어떤 면에 연속적으로 있는 경우에만 내측 그래프의 정점이 인접한다. 평면 그래프의 이중 그래프의 내적 그래프는 원래 평면 그래프의 내적 그래프와 동일하다.^[29]

일반 다면체 또는 단순 다면체의 경우, 모든 입사 가장자리의 중간점을 통과하는 평면에 의해 다면체의 각 정점을 잘라내는 연산에 의해 내적 그래프 연산을 기하학적으로 나타낼 수 있다.^[30] 이 수술은 두 번째 잘림,^[31] 퇴보 잘림 ^[32]또는 수리로 다양하게 알려져 있다.^[33]

총 그래프

그래프 G의 총 그래프 T(G)는 G의 원소(수직 또는 가장자리)와 정점이 같으며, 두 원소가 입사하거나 인접할 때마다 두 원소 사이에 가장자리가 있다. G의 각 가장자리를 세분화한 다음 분할된 그래프의 정사각형을 취함으로써 총 그래프를 얻을 수도 있다.^[34]

멀티그래프

G의 선 그래프의 개념은 G가 다문자일 경우에 자연스럽게 확장될 수 있다. 이 경우, 이러한 그래프의 특성화는 단순화할 수 있다: clique 파티션에 관한 특성화는 더 이상 두 정점이 같은 패거리에 속하지 않도록 막을 필요가 없으며, 금지된 그래프에 의한 특성화에는 9개 대신 7개의 금지된 그래프가 있다.^[35]

그러나 다중 그래프의 경우 동일한 선 그래프를 갖는 비이형 그래프 쌍의 수가 더 많다. 예를 들어 완전한 초당적 그래프 K는_1,n 쌍극형 그래프와 같은 선 그래프를 가지고 있고, 섀넌 다중그래프는 가장자리 수가 같다. 그럼에도 불구하고, 휘트니의 이소모르프 정리와 유사한 점은 여전히 이 경우에 도출될 수 있다.^[12]

선 디그그래프

선 그래프를 지시된 그래프에 일반화하는 것도 가능하다.^[36] G가 방향 그래프인 경우 방향 선 그래프 또는 선 디그그래프는 G의 각 가장자리에 대해 하나의 꼭지점을 가진다. u에서 v로 그리고 g에서 w에서 x로 향하는 가장자리를 나타내는 두 개의 꼭지점은 v = w일 때 선 디그그래프에서 uv에서 wx까지 에지로 연결된다. 즉, G의 선 디그그래프의 각 가장자리는 G의 길이 2 방향 경로를 나타낸다. de Bruijn 그래프는 완전한 방향 그래프에서 시작하여 방향선 그래프를 형성하는 이 과정을 반복함으로써 형성될 수 있다.^[37]

가중선 그래프

선 그래프 L(G)에서 원래 그래프 G의 각 도 k 정점은 선 그래프에 k(k - 1)/2 에지를 만든다. 많은 유형의 분석에서 이는 G의 고차 노드가 선 그래프 L(G)에서 과대 표시됨을 의미한다. 예를 들어, 원래 그래프 G의 꼭지점에 대한 무작위 이동을 고려해 보십시오. 이것은 일부 주파수 f와 함께 어떤 에지 e를 통과할 것이다. 반면에 이 에지 e는 선 그래프 L(G)에서 v라고 하는 고유한 꼭지점에 매핑된다. 지금 우리가 선 그래프의 정점에 대해 같은 유형의 무작위 걷기를 수행한다면, v가 방문되는 빈도는 f와 완전히 다를 수 있다. 만약 우리의 엣지 e in G가 O(k)의 노드에 연결되었다면, 그것은 선 그래프 L(G)에서 O(k²)를 더 자주 통과할 것이다. 다른 방법으로, 휘트니 그래프 이소모르퍼시즘 정리는 선 그래프가 거의 항상 원래의 그래프 G의 위상들을 충실하게 부호화한다는 것을 보장하지만, 이 두 그래프에 있는 역학이 단순한 관계를 갖는다는 것을 보장하지는 않는다. 하나의 해결책은 가중 선 그래프, 즉 가중 에지가 있는 선 그래프를 구성하는 것이다. 이것을 하는 데는 몇 가지 자연스러운 방법이 있다.^[38] 예를 들어, 그래프 G의 에지 d와 e가 도 k의 정점 v에서 발생하는 경우, 선 그래프 L(G)에서 두 꼭지점 d와 e를 연결하는 에지에 무게 1/(k - 1)을 부여할 수 있다. 이 방법으로 G의 모든 에지(두 끝 모두 도 1의 정점에 연결되지 않은 경우)에는 에지가 G에 가지고 있는 두 끝 단에 해당하는 선 그래프 L(G)에 강도 2가 있을 것이다. 가중선 그래프의 이 정의를 원래 그래프 G가 지시되거나 가중치가 부여된 경우로 확장하는 것은 간단하다.^[39] 모든 경우에 원칙은 선 그래프 L(G)이 원래의 그래프 G의 위상뿐만 아니라 역학을 반영하도록 하는 것이다.

하이퍼그래프의 선 그래프

하이퍼그래프의 가장자리는 임의의 집합 집합을 형성할 수 있으므로, 하이퍼그래프의 선 그래프는 집합 집합의 교차 그래프와 동일하다.

불연속도 그래프

D(G)로 표시된 G의 분리성 그래프는 다음과 같은 방식으로 구성된다. G의 각 가장자리에서 D(G)로 정점을 만들고 G의 두 가장자리에서 정점을 공통으로 가지지 않는 모든 두 가장자리에서 D(G)의 해당 정점 사이에 에지를 만든다.^[40] 즉, D(G)는 L(G)의 보완 그래프인 것이다. D(G)의 클라이크는 L(G)의 독립 집합에 해당하며, 그 반대의 경우도 마찬가지다.

메모들

참조

외부 링크

• 선 그래프, 그래프 클래스 포함 시 정보 시스템
• Weisstein, Eric W. "Line Graph". MathWorld.