자기 조직 지도

이 문서는 Wikipedia의 품질 기준을 충족하기 위해 청소가 필요할 수 있습니다. 정리 이유가 지정되지 않았습니다. 가능하다면 이 문서의 개선에 협조해 주십시오.(2011년 6월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍을 확인)

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

자기조직화 맵(SOM) 또는 자기조직화 피쳐 맵(SOFM)은 데이터의 토폴로지 구조를 유지하면서 고차원 데이터 세트를 저차원(일반적으로 2차원)으로 표현하기 위해 사용되는 비지도 기계 학습 기술입니다.예를 들어$,$ $n개$의 \$displaystyle$n $관측치$에서 측정된 p$\style$p 변수가$$ 있는 $데이터{\displaystyle }$ 세트는 변수에 대해 유사한 값을 가진 관측치 군집으로 표현될 수 있다.그러면 이러한 군집을 2차원 "지도"로 시각화하여 근위부 군집의 관측치가 원위부 군집의 관측치보다 더 유사한 값을 가질 수 있습니다.이를 통해 고차원 데이터를 보다 쉽게 시각화하고 분석할 수 있습니다.

SOM은 인공 신경망의 한 종류이지만 다른 인공 신경망에 의해 사용되는 오류 수정 학습(예: 경사 강하 역 전파)이 아닌 경쟁 학습을 사용하여 훈련된다.SOM은 1980년대 핀란드인 Teuvo Kohonen 교수가 도입했기 때문에 Kohonen 지도 또는 Kohonen ^[1][2]네트워크로 불리기도 한다.코호넨 지도 또는 네트워크는 1970년대^[3] 신경계의 생물학적 모델과 1950년대 ^[4]앨런 튜링으로 거슬러 올라가는 형태 형성 모델을 기반으로 계산적으로 편리한 추상화 건물이다.

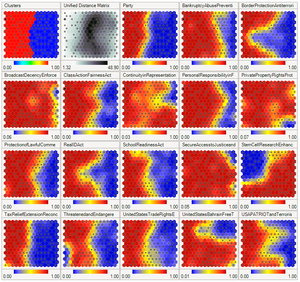
개요

자기조직 지도는 대부분의 인공신경망과 마찬가지로 훈련과 지도 작성의 두 가지 모드로 동작합니다.첫째, 훈련은 입력 데이터 세트('입력 공간')를 사용하여 입력 데이터('지도 공간')의 저차원적 표현을 생성한다.둘째, 매핑은 생성된 맵을 사용하여 추가 입력 데이터를 분류합니다.

대부분의 경우 훈련의 목표는 p차원의 입력공간을 2차원의 지도공간으로 표현하는 것입니다.구체적으로는 변수가 p개인 입력공간은 p차원을 갖는다고 한다.지도 공간은 "노드" 또는 "뉴론"이라고 불리는 구성요소로 구성되며, 2차원의 ^[5]육각형 또는 직사각형 그리드로 배열됩니다.노드의 수와 배열은 데이터의 분석과 탐구의 더 큰 목표에 기초하여 미리 지정된다.

맵 공간 내의 각 노드는 입력 공간 내의 노드 위치인 "무게" 벡터에 관련지어진다.지도 공간의 노드가 고정된 상태를 유지하는 동안, 훈련은 지도 공간에서 유도된 토폴로지를 망치지 않고 입력 데이터를 향해 무게 벡터를 이동하는 것(유클리드 거리 등의 거리 메트릭 감소)으로 구성됩니다.훈련 후 맵은 입력 공간 벡터에 가장 가까운 무게 벡터(최소 거리 메트릭)를 가진 노드를 찾아 입력 공간에 대한 추가 관측치를 분류하기 위해 사용할 수 있다.

학습 알고리즘

자기조직화 맵에서의 학습의 목적은 네트워크의 다른 부분이 특정 입력 패턴에 동일하게 응답하도록 하는 것입니다.이것은 부분적으로 시각, 청각 또는 다른 감각 정보가 인간의 ^[6]뇌에서 대뇌 피질의 분리된 부분에서 어떻게 처리되는지에 의해 동기 부여된다.

뉴런의 가중치는 작은 랜덤 값으로 초기화되거나 가장 큰 두 개의 주성분 고유 벡터에 의해 확장된 부분 공간에서 균등하게 샘플링됩니다.후자의 대안에서는 초기 체중은 이미 SOM 체중의 ^[7]근사치를 제공하기 때문에 학습 속도가 훨씬 빠르다.

매핑 중에 예상되는 벡터의 종류를 가능한 한 가깝게 나타내는 다수의 예제 벡터를 네트워크에 공급해야 합니다.이러한 예는 보통 반복으로 여러 번 관리됩니다.

이 트레이닝에서는, 경쟁력 있는 학습을 활용합니다.훈련 예가 네트워크에 공급될 때, 모든 무게 벡터에 대한 유클리드 거리가 계산됩니다.무게 벡터가 입력과 가장 유사한 뉴런을 최적 매칭 단위(BMU)라고 합니다.SOM 그리드에서 BMU와 BMU에 가까운 뉴런의 무게는 입력 벡터를 향해 조정된다.변화의 크기는 시간과 BMU로부터의 그리드 거리에 따라 감소한다. 무게 벡터_v W(s)를 가진 뉴런 v에 대한 업데이트 공식은

$display W$$W_{v}(s)+\$theta$(u,v,s)\$cdot $\alpha(s)\cdot(D(t)-$W_{$v}(s$

여기서 s는 단계 지수, t는 훈련 샘플에 대한 지수, u는 입력 벡터 D(t)에 대한 BMU의 지수, α(s)는 단조로운 감소 학습 계수, β(u, v, s)는 단계 ^[8]s에서 뉴런 u와 뉴런 v 사이의 거리를 제공하는 근린 함수이다.구현에 따라 훈련 데이터 세트를 체계적으로 스캔할 수 있습니다(t는 0, 1, 2...).T-1을 반복한 후, T가 훈련 샘플의 크기이며, 데이터 세트에서 무작위로 추출되거나(부트스트랩 샘플링), 또는 다른 샘플링 방법(잭나이핑 등)을 구현합니다.

근린 함수 δ(u, v, s)(가로방향 상호작용 함수라고도 함)는 BMU(neuron u)와 뉴런 v 사이의 그리드 거리에 따라 달라진다.가장 간단한 형태에서는 BMU에 충분히 가까운 모든 뉴런에 대해 1이고 다른 뉴런에 대해서는 0이지만, 가우스 및 멕시코^[9] 모자 함수도 일반적인 선택입니다.기능 형태에 관계없이 네이버 함수는 시간이 ^[6]지남에 따라 축소됩니다.처음에는 동네가 넓으면 자기조직화도 글로벌 규모로 이뤄진다.주변이 단지 몇 개의 뉴런으로 줄어들었을 때, 무게는 지역 추정치로 수렴되고 있습니다.일부 구현에서는 학습 계수 α와 근린 함수가 s의 증가와 함께 꾸준히 감소하며, 다른 구현에서는 (특히 t가 훈련 데이터 세트를 스캔하는) 단계적 방식으로 T 단계마다 감소한다.

이 처리는 (통상 큰) 사이클 수 µ 동안 각 입력 벡터에 대해 반복됩니다.네트워크는 출력 노드를 입력 데이터 세트의 그룹 또는 패턴과 관련짓습니다.이러한 패턴에 이름을 붙일 수 있는 경우는, 트레이닝 끝난 넷내의 관련 붙여진 노드에 이름을 붙일 수 있습니다.

매핑하는 동안, 하나의 이기는 뉴런이 있을 것입니다: 무게 벡터가 입력 벡터에 가장 가까운 곳에 있는 뉴런입니다.이것은 입력 벡터와 무게 벡터 사이의 유클리드 거리를 계산함으로써 간단히 결정될 수 있다.

입력 데이터를 벡터로서 나타내는 것에 중점을 두고 있지만, 디지털로 표현할 수 있고, 적절한 거리 측정이 관련지어져 있으며, 트레이닝에 필요한 조작이 가능한 어떠한 오브젝트도 자기 조직화 맵을 작성하는데 사용할 수 있다.여기에는 행렬, 연속 함수 또는 기타 자기 조직화 맵이 포함됩니다.

변수

필요한 변수는 다음과 같습니다. 굵은 글씨로 표시된 벡터는

• $\displaystyle$s는$$ 현재 반복입니다.
• $§$ $(\displaystyle$ \displayda$)$는 반복 제한입니다.
• ${\displaystyle t}${\$displaystyle$ t$}$는 입력$$ 데이터 $세트{\displaystyle \mathbf{}}$D {\$displaystyle\mathbf {D}$의 타깃 입력 데이터 벡터의 인덱스입니다$.$
• ${\displaystyle D(}$ $)$ {$displaystyle {D}(t)}$은(는) 타겟 입력 데이터 벡터입니다.
• $\displaystyle$v는 맵 내 노드의$$ 인덱스입니다.
• ${\displaystyle {}_{}}$v \$displaystyle$ $\mathbf {W} _{v}$는 노드$v$의 현재$무게$ 벡터입니다.
• ${\displaystyle }$u$\displaystyle$u는 맵에서$$ 가장 적합한 유닛(BMU)의 ${\displaystyle \mathrm{인덱스}}$입니다.
• ${\displaystyle \S }$ (${\displaystyle u}$, ${\displaystyle v}$,$$s ){ display \$theta ( u$, v ,$$s )는 BMU로부터의 거리에 의한 구속으로, 보통 근린 함수라고 ${\displaystyle \mathrm{불립니다}}$.
• ${\displaystyle }$α${\displaystyle }$(${\displaystyle s}$) { $displaystyle \alpha ( s$ )는 반복 진행으로 인한 학습 제한입니다.

알고리즘.

1. 맵에서 노드 무게 벡터를 랜덤화합니다.
2. 입력 $벡터{\displaystyle }$D (${\displaystyle t}$) {$displaystyle {D}(t)}$를 랜덤으로 선택합니다.
3. 지도의 각 노드를 이동합니다.
   1. 유클리드 거리 공식을 사용하여 입력 벡터와 지도 노드의 가중치 벡터 사이의 유사성 찾기
   2. 가장 짧은 거리를 생성하는 노드를 추적합니다(이 노드는 가장 적합한 유닛(BMU)입니다).
4. BMU 인근 노드(BMU 자체 포함)를 입력 벡터에 더 가깝게 당겨 가중치 벡터를 업데이트합니다.
   1. ${\displaystyle W_{v}(s+1)=W_{v}+\theta(u,v,s)\cdot \alpha(s)\cdot(D(t)-W_{v}(s))}$
5. $\displaystyle$s를$$ 늘려 s$<\displaystyle$ s $<\lambda >$ 동안 부터 반복합니다.

대체 알고리즘

1. 지도 노드의 가중치 벡터 랜덤화
2. 입력 데이터 세트의 각 입력 벡터 이동
   1. 지도의 각 노드를 이동합니다.
      1. 유클리드 거리 공식을 사용하여 입력 벡터와 지도 노드의 가중치 벡터 사이의 유사성 찾기
      2. 가장 짧은 거리를 생성하는 노드를 추적합니다(이 노드는 가장 적합한 유닛(BMU)입니다).
   2. BMU 인근 노드(BMU 자체 포함)를 입력 벡터에 가깝게 당겨 업데이트합니다.
      1. ${\displaystyle W_{v}(s+1)=W_{v}+\theta(u,v,s)\cdot \alpha(s)\cdot(D(t)-W_{v}(s))}$
3. $\displaystyle$s를$$ 늘려 s$<\displaystyle$ s $<\lambda >$ 동안 부터 반복합니다.

초기화 옵션

최종 체중의 좋은 근사치로 초기 체중을 선택하는 것은 자기 조직 지도를 포함한 인공 신경망의 모든 반복 방법에 대해 잘 알려진 문제이다.Kohonen은 원래 ^[10]무게의 무작위 개시를 제안했다. (이 접근방식은 위에서 설명한 알고리즘에 의해 반영된다.)최근에는 결과의 ^[11]정확한 재현성 때문에 첫 번째 주성분 공간에서 초기 지도 가중치를 선택하는 주성분 초기화가 인기를 끌고 있다.

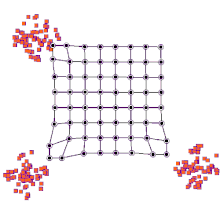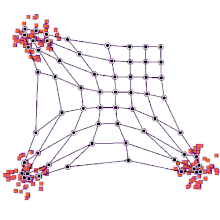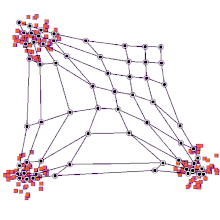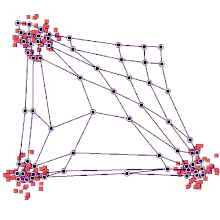
그러나 1차원 맵에 대한 주성분 초기화와 랜덤 초기화를 주의 깊게 비교한 결과 주성분 초기화의 장점이 보편적이지 않은 것으로 나타났습니다.최적의 초기화 방법은 특정 데이터 세트의 형상에 따라 달라집니다.데이터 세트에 근사한 주 곡선이 첫 번째 주성분(사각형 세트)에 비가치와 선형으로 투영될 수 있을 때 주성분 초기화가 선호되었다.그러나 비선형 데이터 세트의 경우 랜덤 시작이 ^[12]더 잘 수행되었습니다.

해석

SOM을 해석하는 방법에는 두 가지가 있습니다.전체 이웃의 훈련 단계 체중은 같은 방향으로 이동하기 때문에, 유사한 항목은 인접한 뉴런을 자극하는 경향이 있다.따라서 SOM은 유사한 샘플이 서로 밀접하게 매핑되고 서로 다른 샘플이 서로 다른 의미 맵을 형성합니다.이는 ^[14][15][16]SOM의 U-Matrix(주변 세포의 무게 벡터 사이의 유클리드 거리)에 의해 시각화될 수 있다.

또 다른 방법은 입력 공간에 대한 포인터로서 신경 체중을 생각하는 것입니다.이들은 교육 표본 분포의 이산적 근사치를 형성한다.더 많은 뉴런이 훈련 샘플 농도가 높은 지역을 가리키고 샘플이 부족한 지역은 더 적습니다.

SOM은 주성분 분석(PCA)^[17]의 비선형 일반화로 간주될 수 있습니다.인공 및 실제 지구물리학 데이터를 모두 사용하여 SOM은 경험적 직교 함수(EOF) 또는 PCA와 같은 기존 특징 추출 방법보다 많은 이점을^[18][19] 가지고 있는 것으로 나타났다.

원래 SOM은 최적화 문제에 대한 해결책으로 공식화되지 않았습니다.그럼에도 불구하고, SOM의 정의를 수정하고 유사한 ^[20]결과를 제공하는 최적화 문제를 공식화하려는 여러 시도가 있었다.예를 들어 탄성 지도는 탄성의 기계적 은유를 사용하여 주요 ^[21]다지관에 근사합니다. 즉, 탄성 막과 판입니다.

예

피셔의 홍채꽃 데이터

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 소스되지 않은 소재는 문제가 발생하여 삭제될 수 있습니다. (2010년 2월) (이 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다)

이 섹션에는 독창적인 연구가 포함되어 있을 수 있습니다. 클레임을 확인하고 인라인 인용을 추가하여 개선해 주십시오. 독창적인 연구로만 구성된 진술은 삭제되어야 한다.(2017년 6월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

n×m의 노드 배열에 대해 생각해 봅시다.노드는 각각 가중치 벡터를 포함하고 배열 내의 위치를 인식합니다.각 가중치 벡터는 노드의 입력 벡터와 동일한 차원을 가집니다.가중치는 처음에 랜덤 값으로 설정할 수 있습니다.

이제 지도에 입력이 필요합니다.색상은 빨간색, 녹색 및 파란색 구성요소로 나타낼 수 있습니다.따라서, 우리는 다음과 같이 생성되는 δ 이상의 자유 벡터 공간의 단위 큐브에서 색을 벡터로 나타낼 것이다.

R = <255, 0, 0>

G = <0, 255, 0>

B = <0, 0, 255>

표시된 그림은

데이터^{[Note 1]} 세트에 대한 교육 결과를 비교합니다.

3색 = [255, 0, 0], [0, 255, 0], [0, 0, 255]

8컬러 = [0, 0, 0], [0, 255, 0], [0, 255, 0], [0, 255, 0], [0, 255, 255], [255, 0, 255], [255, 255], [255, 255]

그리고 원본 이미지들.그 둘 사이의 현저한 유사성에 주목하라.

마찬가지로, 피셔의 홍채에서 학습률이 0.1인 40×40의 뉴런 그리드를 250회 반복 훈련한 후, 지도는 이미 종 간의 주요 차이를 감지할 수 있다.

다른.

• 프로젝트의 우선순위 부여 및 선택
• 석유 및 가스 탐사를 위한 지진면 분석
• 고장 모드 및 영향 분석^[24]
• 아트워크의 작성
• 대규모 데이터 집합에서 대표 데이터 찾기(예: 생태계를 ^[26]위한 대표 종, 에너지 시스템^[27] 모델의 대표 일).

대체 수단

• Generative Topographic Map(GTM; 생성형 지형도)은 SOM의 대체 수단일 가능성이 있습니다.GTM은 입력공간에서 맵공간으로의 매끄럽고 연속적인 매핑을 명시적으로 필요로 한다는 점에서 토폴로지 보존입니다.그러나 실질적인 의미에서 이 위상 보존 척도는 부족하다.^[28]
• Time Adaptive Self-Organizing Map(TASOM; 시간적응형 자기조직지도) 네트워크는 기본 SOM의 확장입니다.TASOM은 적응형 학습 속도 및 주변 기능을 사용합니다.또한 네트워크를 입력 공간의 스케일링, 변환 및 회전에 불변하게 하는 스케일링 파라미터도 포함되어 있습니다.TASOM 및 TASOM의 변형은 적응형 클러스터링, 다단계 임계값 설정, 입력 공간 근사 및 활성 등고선 ^[29]모델링을 포함한 여러 애플리케이션에서 사용되어 왔습니다.또한, 레벨의 수와 노드 ^[30]수가 환경에 적응할 수 있는 TASOM 네트워크로 구성된 노드를 가진 바이너리 자연 트리와 유사한 바이너리 트리 TASOM 또는 BTASOM이 제안되었다.
• Growing Self-organizing Map(GSOM; 자기조직화 맵)은 자기조직화 맵의 변종입니다.GSOM은 SOM에서 적절한 지도 크기를 식별하는 문제를 해결하기 위해 개발되었습니다.최소 노드 수(보통 4개)로 시작하여 휴리스틱을 기반으로 경계에서 새로운 노드를 성장시킵니다.데이터 분석가는 확산률이라는 값을 사용하여 GSOM의 성장을 제어할 수 있습니다.
• 탄성 지도^[31] 접근법은 탄성 에너지의 최소화에 대한 아이디어를 스플라인 보간으로부터 차용한다.학습에서는 최소 제곱 근사 오차로 2차 굽힘 및 스트레칭 에너지의 합을 최소화합니다.
• 컨포멀 매핑을 사용하여 연속 표면의 그리드 노드 간에 각 훈련 샘플을 보간하는 컨포멀 접근법.이 방법에서는 1대 1의 매끄러운 매핑이 가능합니다.
• Oriented and Scalable Map(OS-Map)은 네이버 기능과 당첨자 선택을 ^[34]일반화합니다.동종 가우스 근린 함수는 행렬 지수 함수로 대체됩니다.따라서 지도 공간 또는 데이터 공간에서 방향을 지정할 수 있습니다.SOM은 고정된 척도(=1)를 가지므로 지도는 "관찰 영역을 기술한다".하지만 도메인을 두 번 또는 n번으로 묶은 지도는 어떨까요?여기에는 스케일링 개념이 수반됩니다.OS-Map에서는 척도를 지도에 입력된 최적의 노드 수에 대한 통계적 설명으로 간주합니다.

「 」를 참조해 주세요.

• 신경 가스
• 학습 벡터 양자화
• 액체 상태 기계
• 하이브리드 코호넨 SOM
• 스파스 부호화
• 스퍼스 분산 메모리
• 딥 러닝
• 네오인지트론
• 위상 데이터 분석
• 루스툼, 라비, 아데바요 아델로예, 오로레 시말라.「Kohonen 자기 조직 지도(KSOM)는, BOD5의 MLP-ANN 예측 모델을 강화하기 위한 기능을 추출했습니다」국제 심포지엄에서:지속 가능한 수자원 관리를 위한 예측 불확실성의 정량화 및 감소 - 국제지질물리학연합(IUG) 제24차 총회, 181-187.27페이지.

메모들

레퍼런스