정량 회귀 분석

다음에 대한 시리즈 일부
회귀분석
모델
선형 회귀 분석 단순 회귀 분석 다항식 회귀 분석 일반 선형 모형
일반화 선형 모형 이산선택 이항 회귀 분석 이항 회귀 분석 로지스틱 회귀 분석 다항 로지스틱 회귀 분석 혼합 로짓 프로빗 다항 프로빗 주문형 로짓 주문 프로빗 포아송
다단계 모델 고정 효과 랜덤 효과 선형 혼합 효과 모형 비선형 혼합효과 모형
비선형 회귀 분석 비모수 세미파라메트릭 로버스트 퀀틸레 동위원소 주성분 최소 각도 국부적 세그먼트화
변수 내 오류
추정
최소 제곱 선형 비선형
보통 가중치 일반화
부분적 합계 비음성 능선 회귀 분석 정규화된
최소 절대 편차 반복적으로 다시 가중치 부여 베이시안 베이시안 다변량
배경
회귀 유효성 검사 평균 및 예측 반응 오차 및 잔차 적합도 학생화 잔차 가우스-마르코프 정리
수학포털
v t

정량 회귀 분석은 통계학과 계량학에서 사용되는 회귀 분석의 한 유형이다. 최소 제곱 방법은 예측 변수의 값에 대한 반응 변수의 조건부 평균을 추정하는 반면, 분위 회귀 분석에서는 반응 변수의 조건부 중위수(또는 기타 분위수)를 추정한다. 양자 회귀는 선형 회귀의 조건이 충족되지 않을 때 사용되는 선형 회귀의 확장이다.

장점과 응용 프로그램

일반 최소 제곱 회귀 분석과 비교하여 정량적 회귀 분석의 한 가지 장점은 정량적 회귀 추정치가 반응 측정에서 특이치에 대해 더 강하다는 것이다. 그러나, 퀀텀 회귀 분석의 주된 매력은 이를 넘어서며 조건부 퀀텀 기능이 관심사일 때 유리하다. 중심적 경향과 통계적 산포의 다른 척도는 변수들 간의 관계에 대한 보다 포괄적인 분석을 얻는데 유용할 수 있다.^[1]

생태학에서, 계량형 회귀는 그러한 변수의 수단 사이에 관계가 없거나 단지 약한 관계만 있는 경우에 변수들 간의 보다 유용한 예측 관계를 발견하는 방법으로 제안되고 이용되었다. 생태학에서 계량적 회귀 분석의 필요성과 성공은 다른 변수 범위에 대해 한 변수의 불균등한 변동을 갖는 데이터로 이어지는 서로 다른 요인 간의 상호작용의 복잡성에 기인한다.^[2]

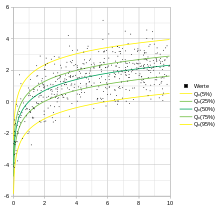
또 다른 퀀텀 회귀 분석은 성장 차트의 영역에 적용되며, 여기서 백분위수 곡선은 비정상적인 성장을 선별하는 데 일반적으로 사용된다.^[3][4]

역사

중앙 회귀 기울기를 추정하는 아이디어, 절대 편차의 합계를 최소화하기 위한 주요 정리, 중앙 회귀 건설을 위한 기하학적 알고리즘은 1760년 두브로브니크 출신의 예수회 카톨릭 신부인 루제르 조십 보슈코비치에 의해 제안되었다.^{[1]: 4 [5]} 그는 지구의 타원성에 관심을 가졌는데, 그 자전이 적도에 폭포를 일으키게 할 수 있다는 아이작 뉴턴의 제안에 기초하여 극지방에서 그에 상응하는 평탄화로 지구의 타원성에 관심이 있었다.^[6] 그는 마침내 표면 형상의 세 가지 관측에서 회전하는 행성의 적도를 결정하는 첫 번째 기하학적 절차를 만들었다. 더 중요한 것은 양자 회귀의 경우, 그는 최소한의 절대적 기준에 대한 최초의 증거를 개발할 수 있었고 1805년 레전드레가 도입한 최소 제곱보다 50년 앞서 있었다.^[7]

다른 사상가들은 소위 "메토데 데 상황"을 발전시킨 피에르 시몬 라플레이스와 같은 보슈코비치의 생각을 바탕으로 구축하기 시작했다. 이것은 프랜시스 엣지워스의 복수 중위수^[8] - 중앙분리대 회귀에 대한 기하학적 접근 -을 이끌어냈고 심플렉스 방법의 전조로 인정받고 있다.^[7] 보슈코비치, 라플라스, 엣지워스의 작품은 로저 쿤커가 양적 회귀에 기여한 서곡으로 인정받았다.

대형 데이터 세트에 대한 중앙분리대 회귀 계산은 20세기 후반에 컴퓨터가 널리 채택되기 전까지 통계학자들 사이에서 역사적으로 인기 부족을 초래한 최소 제곱법에 비해 상당히 지루하다.

퀀텀스

계량형 회귀 분석은 종속 변수의 조건부 계량형을 설명 변수의 선형 함수로 표현한다. 다음 절에서 조건부 정량화를 논의하기 전에 이 절에서 보여주듯이, 정량화가 최소화 문제의 해결책으로 표현될 수 있다는 것이 정량적 회귀의 실용성에 결정적이다.

랜덤 변수의 수량

$Y{\displaystyle }$ ${\displaystyle$ Y$}$을(를) 누적 분포 함수 $F{\displaystyle {}_{}}$ ${\displaystyle Y_{}Y}$ ${\displaystyle )}$= ${\displaystyle P(Y}$ ${\displaystyle \le }$ y${\displaystyle }$) ${\displaystyle F_{Y}(y)=P(Y\leq$ y$)}$을(를) 가진 실제 값 랜덤 변수가 되도록$$ 한다$.$ Y의 $\tau {\displaystyle }$ ${\displaystyle \tau }$은(는) 다음과 같이 주어진다.

${\displaystyle q_{Y}(\tau )=F_{Y}^{-1}(\tau )=\inf \left\{y:F_{Y}(y)\geq \tau \오른쪽\}}$

여기서$$$\tau {\displaystyle }$(${\displaystyle 0}$, ${\displaystyle 1}$)${\displaystyle }$. ${\displaystyle \tau \in (0,1$).$}$

손실 함수를 $$()= y (- ( < ${\displaystyle \rho _{\tau$ _$}(y)=y(\tau$ -$\mathb {$I} $_{(y<0)})$로 정의하십시오 $여기$서 I {\$displaystystyle \mathb {I}$은 지표 함수입니다.

$u{\displaystyle }$ ${\displaystyle u}$ :($$^[1]pp. 5–6)와 관련하여$$ $Y{\displaystyle }$ -${\displaystyle u}$ ${\displaystyle Y-u}$의 예상 손실을 최소화함으로써 특정 계량형을 찾을 수 있다.

${\displaystyle q_{Y}(\tau )={\underset {u}{\\mbox{arg min}}E(\rho _{\tau }(Y-u))={\cHBET {u}{\mbox{arg min}}{\biggl \{}{}(\tau -1)\int_{-\infit }^{u}(y-u)F_{Y}(y)+\tau \int _{u}^{\infit }(y-u)dF_{Y}(y){\biggr \}}.}$

이는 라이프니즈 적분 규칙을 적용하여 예상 손실의 파생상품을 계산하여 0으로 설정하고, $q{\displaystyle {}_{}}$ ${\$을(를) 해결책으로 두면$$ 알 수 있다.

${\displaystyle 0=(1-\tau )\int_{-\dF_{\tau }^{q_{}-{\tau \int _{q_{\tau }}^{\dF_{Y}(y).}$

이 방정식은 다음과 같이 감소한다.

${\displaystyle 0=F_{Y}(q_{\tau }-\tau,})$

그 다음으로는

${\displaystyle F_{Y}(q_{\tau }}=\tau .}$

솔루션 ${\$이(가) 고유하지 않다면, 랜덤 변수 Y의 $quant{\displaystyle }$ ${\displaystyle \tau }$분위수를$$ 얻으려면 가장 작은 솔루션을 취해야 한다.

예

$Y{\displaystyle }$ ${\displaystyle Y}$을(를$)$ 동일한 확률로$$ $y{\displaystyle }$ ${\displaystyle i_{}}$${\displaystyle }$= ${\displaystyle \mathrm{i}}$$$= ${\displaystyle$ $y_$${i}=i$$}$ 값을$$ 갖는 이산형 $랜덤$ 변수로 $두십시오$. 작업은 Y의 중위수를 찾는 것이므로 ${\displaystyle \mathrm{\tau }}$=${\displaystyle 0}$.5 $[\displaystyle \tau =0.5}$ 값이 선택된다$$. $그러면$ Y -${\displaystyle u}$ ${\displaystyle Y-u}$의 예상 손실은

${\displaystyle L(u)=E(\rho _{\tau }(Y-u))={\frac {(\tau -1)}{9}\sum _{y_{i}<u}}}$${\displaystyle(y_{i}-u)}$${\displaystyle +{\frac {\tau }{9}\sum _{y_{i}\geq u}}}$${\displaystyle(y_{i}-u)}$${\displaystyle ={\frac {0.5}{9}}{\Bigl (}})$${\displaystyle -}$${\displaystyle \sum _{y_{i}<u}}$${\displaystyle(y_{i}-u)}$${\displaystyle +\sum _{y_{i}\geq u}}}$${\displaystyle(y_{i}-u)}$${\displaystyle {\Bigr )}.}$

${\displaystyle 0.}$5${\displaystyle }$/ ${\displaystyle 9\mathrm{}}$ ${\$이(가) 상수이므로$$ 기대 손실 함수에서 빼낼 수 있다(이는 $\tau {\displaystyle }$= 0${\displaystyle \tau =$0.5$}).$ 그러면 u=3에서

${\displaystyle L(3)\propto \sum _{i=1}^{2}}$$(\displaystyle -(i-3)}$${\displaystyle +\sum _{i=3}^{9}}}$$(\displaystyle (i-3)}$${\displaystyle =[(2+1)++(0+1+2+...+6)]=24.}$

u가 1단위 증가했다고 가정합시다. 그런 다음 u를 4로 변경하면$$ 예상되는${\displaystyle \mathrm{손실}}$이${\displaystyle }$(${\displaystyle }$3${\displaystyle }$) -${\displaystyle }$(${\displaystyle }$6${\displaystyle }$) = -$$ {\$displaystyle (3)-(6)=-3}$만큼 변경된다. 만약, u=5가 기대되는 손실이

${\displaystyle L(5)\propto \sum _{i=1}i+\sum _{i=0}i=20,}$

그리고 어떤 변화도 예상되는 손실을 증가시킬 것이다. 따라서 u=5는 중위수다. 아래 표는 u의 다른 값에 대한 ${\displaystyle \mathrm{예상}}$ 손실($0{\displaystyle \mathrm{.}}$5${\displaystyle }$/ ${\displaystyle 9\mathrm{}}$ ${\$로 나눈 값$)$을 나타낸다.

u	1	2	3	4	5	6	7	8	9
예상손실	36	29	24	21	20	21	24	29	36

직감

$\tau {\displaystyle }$= 0.${\displaystyle 5}$ ${\displaystyle \tau =$0.5$}$을(를) 고려하여 ${\displaystyle q_{}}$ q ${\$ $\}\}\}$에 대한 초기 추측으로 두십시오. q에서 평가된 예상 손실은 다음과 같다.

${\displaystyle L(q)=-0.5\int _{-\ft }^{q}(y-q)dF_{Y}(y)+0.5\int _{q}^{\ft }(y-q)dF_{Y}(y).}$

예상손실을 최소화하기 위해 q의 값을 조금씩 움직여 예상손실이 상승할지 하락할지 살펴본다. q를 1단위로 증가시킨다고 가정합시다. 그러면 예상 손실의 변화는

${\displaystyle \int _{-\int _{-}{q}1dF_{Y}-(y)-\int _{q}^{\infit }{1dF_{Y}(y).}$

는 만일 q보다 작다는 방정식의 첫번째 임기는 FY(q){\displaystyle F_{Y}(q)}와 방정식의 두번째 임기는 1FY(q){\displaystyle 1-F_{Y}(q)}−. 그러므로, 기대 손실 함수의 변화 부정적이다 만일 FY(q)<>0.5{\displaystyle F_{Y}(q)<, 0.5},. 나dian. 마찬가지로 q를 1단위로 줄이면 q가 중위수보다 큰 경우에만 기대손실함수의 변화가 음수다.

기대손실함수를 최소화하기 위해 q가 중위수보다 작으면(더 큰) L(q)을 q가 중위수에 도달할 때까지 증가(감소)할 것이다. 최소화의 이면에 있는 아이디어는 q보다 크거나 작은 점(밀도에 가중치 부여)의 수를 세고, ${\displaystyle q}$를 $㎛[\displaystyle 100\tau$ $\}\%$ 이상의 점으로 이동시키는 것이다.

검체 퀀텀

$다음$과 같은 최소화 문제를 해결하여 by ${\displaystyle \tau }$ 샘플$$ 퀀텀을 얻을 수 있다.

${\displaystyle {\hat{q}_{\tau }={\underset {q\in \mathb {R}{\mbox{arg min}}}\sum _{i=1}^{n}\rho _{\tau}(y_{i}-q),}}$

${\displaystyle ={\underset {q\in \mathbb {R} }{\mbox{arg min}}}\left[(\tau -1)\sum _{y_{i}<q}(y_{i}-q)+\tau \sum _{y_{i}\geq q}(y_{i}-q)\right]}$,

여기서 함수 ${\$는 기울어진 절대값 함수다. 직관은 인구 수량과 같다.

조건부 계량형 및 계량형 회귀 분석

$X{\displaystyle }$ ${\displaystyle X}$이(가$)$ $주어진{\displaystyle }$ Y {\$displaystyle Y}$의 조건부 수량 conditional ${\$$displaystyle \tau$$}$은$($는) $X{\displaystyle }$ ${\displaystyle X}$이(가) $주어진$ Y ${\displaystystyle$ Y}의 조건부 확률 분포의 { ${\\\$dumilique이다.

$displaystyle Q_{Y X}(\tau )=\inf \left\{y:$$F_{Y$ X$}(y)\geq \tau \right$

자본 $Q{\displaystyle }$ ${\displaystyle Q}$를 사용하여 임의 변수임을 나타내는 조건부 계량형을 나타낸다.

$\tau {\displaystyle }$ ${\displaystyle \tau }$의 퀀텀 회귀 분석에서는 조건부 $quant{\displaystyle }${\$displaystyle \tau }$ th의$$ τ이 설명 변수의 선형 함수로 주어진다고 가정한다.

${\displaystyle Q_{}}$ ${\displaystyle Y_{}}$ ${\displaystyle X_{}}$ (${\displaystyle \tau }$ )${\displaystyle }$= ${\displaystyle X}$ ${\displaystyle {}_{}}$ ${\displaystyle {\tau }_{}}$ ${\$ $\}\}\}.$

$Y{\displaystyle }$ ${\displaystyle Y}$의 분포 함수를 고려할 때$$β ${\displaystyle {\tau }_{}}$ ${\$을(를) 풀어서 얻을 수 있다$$.

${\displaystyle \beta _{\tau }={\underset{\bethb {R}^{k}}{\mbox{arg min}}}E(\rho _{\tau })(Y-X\beta )}$

샘플 아날로그를 해결하면 $\beta {\displaystyle }$ ${\displaystyle \beta }$의 추정기가 제공된다$.$

${\displaystyle {\hat {\beta _{\tau }={\underset{\in \mathb {R}^{k}}{\mbox{arg min}}\sum _{i=1}^{n}(\rho _{i}-X_{i}\beta)}.}$

$\tau {\displaystyle }$=${\displaystyle 0}$.5 ${\displaystyle \tau$= 0$.5}$일 때 손실$$ 함수 ${\$은 절대값 함수에 비례하므로 중위수 회귀는 최소 절대 편차에 의한 선형 회귀와 동일하다는 점에 유의하십시오.

회귀 모수에 대한 추정치 계산

양자 회귀 분석에서 발생하는 수학적 형태는 최소 제곱법에서 발생하는 형태와 구별된다. 최소 제곱법은 서브스페이스에 투영하는 것을 수반하는 내부 제품 공간의 문제들에 대한 고려로 이어지며, 따라서 제곱 오차를 최소화하는 문제는 수치 선형대수학에서 문제로 축소될 수 있다. Quantile 회귀 분석에는 이러한 구조가 없으며, 대신 최소화 문제는 선형 프로그래밍 문제로 재조정될 수 있다.

${\displaystyle {\underset {\beta ,u^{+},u^{-}\in \mathbb {R} ^{k}\times \mathbb {R} _{+}^{2n}}{\min }}\left\{\tau 1_{n}^{'}u^{+}+(1-\tau )1_{n}^{'}u^{-} X\beta +u^{+}-u^{-}=Y\right\},}$

어디에

${\displaystyle u_{}^{}}$ j${\displaystyle {}_{}^{}}$+${\displaystyle {}_{}^{}}$= ${\displaystyle max}$ ${\displaystyle (\mathrm{u}}$ j${\displaystyle {}_{}}$, 0${\displaystyle }$) ${\displaystyle u_{j}^{+}=\max(u_{j},0)},$ $$${\displaystyle u_{}^{}}$j${\displaystyle {}_{}^{}}$=${\displaystyle -min({}_{}}$ ${\displaystyle j_{}}$, ${\displaystyle 0}$ ${\displaystyle u_^{j}^{-}=-\min(u_{j},$0),$0)$$}$

심플렉스 방식이나^{[1]: 181} 내부 포인트 방식을^{[1]: 190} 적용해 선형 프로그래밍 문제를 해결할 수 있다.

점근성

$\tau {\displaystyle (0}$, ${\displaystyle 1}$) ${\displaystyle \tau \in (0,1$의 경우, 어떤 규칙성 조건에서는 $\beta {\displaystyle {\stackrel{}{}}_{}}$^${\displaystyle {\stackrel{}{}}_{}}$^ ${\displaystyle {\tau }_{}}${\$displaystyle {\hat{\beta }}}{\tau }}}}}$은(는) 증상이 없는 정상이다.

${\displaystyle {\sqrt{n}({\hat {\beta }}-{\tau }-\beta _{\tau }}}){d}{\n({\wrigharrow }){-1}D^{x}D^{-1}),}}}$

어디에

${\displaystyle D}$= ${\displaystyle E}$(${\displaystyle {}_{}}$ ${\displaystyle Y_{}}$( ${\displaystyle X}$ ${\displaystyle \beta }$) ${\displaystyle X}$ ${\displaystyle {}^{}}$ ${\displaystyle {\prime \mathrm{}}^{}}$) ${\displaystyle D=E(f_{Y})(X\beta )X^{\prime }}$ 및$$ ${\displaystyle {\Omega }_{}}$x =${\displaystyle E}$(${\displaystyle {}^{\mathrm{}}}$X${\displaystyle }$) .$${\$displaysty Oomega$_{$x=E(X^{\primprime}$X)}X)}X$.$$}$

점근법 분산-공분산 행렬의 직접 추정이 항상 만족스러운 것은 아니다. 계량형 회귀 분석 매개변수에 대한 추론은 회귀 순위 점수 검정 또는 부트스트랩 방법을 사용하여 수행할 수 있다.^[9]

어정쩡함

불변성에 대한 배경은 불변 추정기를 참조하거나 불변성을 참조하십시오.

척도 부등식

> ${\displaystyle a>0}$ 및 $\tau {\displaystyle }$[ ${\displaystyle 0,}$ ${\displaystyle 1}$ ${\displaystyle ]}$ ${\displaystyle \tau \in [0,1]}$인 경우

${\displaystyle {\hat {\beta}(\tau ;aY,X)=a{\hat {\beta }}(\tau ;Y,X),}$

${\displaystyle {\hat {\beta}(\tau ;-aY,X)=-a{\hat {\beta }1-\tau ;Y,X).}$

시프트 부등식

$\gamma {\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {}^{}}$ ${\displaystyle k^{}}$ ${\$ R$^{k}$ 및$$${\displaystyle }\tau {\displaystyle }$[ ${\displaystyle 0}$, ${\displaystyle 1}$ ${\displaystyle ]}$ ${\displaystyle \tau \in [0,1]}$인 경우

${\displaystyle {\hat {\beta}}(\tau ;Y+X\gamma,X)={\hat {\beta }}}}(\tau ;Y,X)+\gamma.}$

설계의 재귀화에 대한 등각도

$A${\${\displaystyle \mathrm{displaystyle}}$ A}을(를) p × p {\$displaystyle p\times$ p$}$ 비동기$$ 행렬과 ${\displaystyle \mathrm{and}}$[ ${\displaystyle 0,}$ 1 ${\displaystyle ]}$ ${\displaystyle \tau \in [0,1]}$이(가) 되도록 두십시오.

${\displaystyle {\hat {\beta}(\tau ;Y,XA)=A^{-1}{\hat {\beta }}(\tau ;Y,X)}$

모노톤 변환에 대한 비침습성

$h{\displaystyle }$ ${\displaystyle h}$이(가) $R{\displaystyle \mathbb{}}$ ${\$의 비감소 함수인 경우 다음 invariance 속성이 적용된다$.$

${\displaystyle h(Q_{Y X}(\tau )\equiv Q_{h(Y) X}(\tau).}$

예제 (1):

If ${\displaystyle W=\exp(Y)}$ and ${\displaystyle Q_{Y X}(\tau )=X\beta _{\tau }}$, then ${\displaystyle Q_{W X}(\tau )=\exp(X\beta _{\tau })}$. 평균 회귀 분석은 $E{\displaystyle \mathrm{}}$ (${\displaystyle \ln }$ ${\displaystyle }$( Y${\displaystyle }$)${\displaystyle \ne }$ ${\displaystyle \ln }$ ${\displaystyle }$(${\displaystyle E}$ )${\displaystyle \operatorname {E}(\ln(Y)\neq \nln(\operatorname {E})(Y$)} 이후 동일한 속성을 가지지 않는다$.$

분량 회귀 분석을 위한 베이지안 방법

양분 회귀 분석은 일반적으로 Y X의 조건부 분포에 대한 모수적 우도를 가정하지 않기 때문에 베이시안 방법은 작업 우도를 사용하여 작동한다. 평탄한 선행 하에서의 결과 후행의 모드가 일반적인 정량 회귀 추정치이기 때문에 편리한 선택은 비대칭 라플라시안 가능성이다.^[10] 그러나 후추론은 주의 깊게 해석해야 한다. 양, 왕, 그리고^[11] 그는 유효한 추론을 위해 후분산 조정을 제공했다. 게다가, 양과 그는^[12] 만약 작업 가능성이 경험적 우도로 선택된다면 점증적으로 유효한 후추론을 가질 수 있다는 것을 보여주었다.

양자 회귀 분석을 위한 기계 학습 방법

단순한 선형회귀를 넘어, 양자회귀까지 확장할 수 있는 몇 가지 기계학습법이 있다. 오차 제곱에서 기울어진 절대값 손실 기능으로 전환하면 구배 강하 기반 학습 알고리즘이 평균 대신 지정된 계량형을 학습할 수 있다. 모든 신경망과 딥러닝 알고리즘을 양자 회귀에 적용할 수 있다는 뜻이다.^[13][14] 또한 나무 기반 학습 알고리즘은 계량형 회귀 분석에 사용할 수 있다(예: 무작위 포리스트의 단순 일반화로서 ^[15]계량형 회귀 숲을 참조).

관측 중단 계량형 회귀 분석

반응 변수가 관측 중단 대상인 경우, 추가 분포 가정 없이는 조건 평균을 식별할 수 없지만 조건부 계량형은 종종 식별할 수 있다. 관측 중단 수량 회귀 분석에 대한 최근 연구는 포트노이^[16] 및 왕과 왕을^[17] 참조하십시오.

예(2):

Let ${\displaystyle Y^{c}=\max(0,Y)}$ and ${\displaystyle Q_{Y X}=X\beta _{\tau }}$. Then ${\displaystyle Q_{$$Y^{c} X}(\tau )=\max(0,X\beta _{\tau$ $\}\}).$ 이것이 검열된 정량 회귀 모형이다. 추정된 값은 분포 가정을 하지 않고도 얻을 수 있지만 계산상의 어려움의 원가로, 그 중 일부는 단순한 3단계 검열된 정량 회귀 절차를 근사치로 사용하여 피할 수 있다.^[18][19]

반응 변수에 대한 랜덤 관측 중단의 경우, Portnoy(2003)^[16]의 관측 중단 계량 회귀 분석은 각 관측 중단점을 적절히 재가중하는 것에 기초하여 모든 식별 가능한 정량함수의 일관된 추정치를 제공한다.

구현

수많은 통계 소프트웨어 패키지에는 다음과 같은 정량적 회귀 분석 구현이 포함된다.

• 매트랩 함수 quantreg^[20]
• 버전 6부터 Eviews.^{[citation needed]}
• 그레틀이 가지고 있다. quantreg 명령하다^[21]
• R은 양자 회귀 분석을 구현하는 몇 가지 패키지를 제공하며, 특히 quantreg 로저 쿤커에 의해,^[22] 그러나 또한 gbm,^[23] quantregForest,^[24] qrnn^[25] 그리고 qgam^[26]
• 파이톤, 경유 Scikit-garden^[27] 그리고 statsmodels^[28]
• SAS 통과 proc quantreg (9.2항)^[29] 및 proc quantselect (^[30]9.3항)
• Stata, 를 통해 qreg 명령하다^[31][32]
• 서약팔 와빗, ~를 통해 --loss_function quantile.^[33]
• 매스매티카 패키지 QuantileRegression.m^[34] GitHub의 MathematicaForPrediction 프로젝트에서 주최한다.

참조

추가 읽기

Wikibook R 프로그래밍에는 다음과 같은 주제의 페이지가 있다: Quantile Regression

• Angrist, Joshua D.; Pischke, Jörn-Steffen (2009). "Quantile Regression". Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. pp. 269–291. ISBN 978-0-691-12034-8.
• Koenker, Roger (2005). Quantile Regression. Cambridge University Press. ISBN 978-0-521-60827-5.