각운동량
Angular momentum이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다.세부사항을 할 수 해 . (2021년 2월) (템플릿메시지 및 에 대해 ) |
| 각운동량 | |
|---|---|
 이 자이로스코프는 각운동량이 보존되어 회전 중에도 직립 상태를 유지합니다. | |
공통 기호 | L |
| SI 기준 단위 | kgµs2−1 |
| 보존? | 네. |
파생상품 기타 수량 | L = I = r × p |
| 치수 | M L2T−1 |
| 시리즈의 일부 |
| 고전 역학 |
|---|
물리학에서 각운동량(희소하지만 운동량의 모멘트 또는 회전운동량)은 선형운동량의 회전유사체이다.이것은 보존된 양이기 때문에 물리학에서 중요한 양입니다. 닫힌 계의 총 각운동량은 일정하게 유지됩니다.각운동량은 방향과 크기를 모두 가지며 둘 다 보존됩니다.자전거와 오토바이, 프리스비[1] 강선 탄환, 자이로스코프는 각운동량 보존에 유용한 특성을 가지고 있다.각운동량 보존은 허리케인이[2] 나선형을 형성하고 중성자별의 회전 속도가 높은 이유이기도 하다.일반적으로 보존은 시스템의 가능한 움직임을 제한하지만 고유하게 결정하지는 않습니다.
점 입자에 대한 3차원 각운동량은 전형적으로 유사벡터 r × p로 표현되며, 이는 입자의 위치 벡터 r (일부 기원에 대한)와 그 운동량 벡터의 교차곱이다. 후자는 뉴턴 역학에서 p = mv이다.운동량과 달리, 각운동량은 입자의 위치가 그것으로부터 측정되기 때문에 어디에서 이 원점을 선택하느냐에 따라 달라집니다.
각운동량은 광범위한 양입니다. 즉, 복합 시스템의 총각운동량은 구성 부품의 각운동량의 합입니다.연속적인 강체 또는 유체의 경우, 총 각운동량은 전체 본체에 걸쳐 각운동량 밀도(부피가 0으로 축소될 때 한계 단위 부피당 각운동량)의 부피 적분입니다.
외력이 없는 경우 선형 운동량을 보존하는 것과 마찬가지로, 외부 토크가 없는 경우 각 운동량을 보존한다.토크는 힘과 유사한 각운동량의 변화율로 정의할 수 있습니다.모든 시스템의 순 외부 토크는 항상 시스템의 총 토크와 동일합니다. 즉, 모든 시스템의 모든 내부 토크의 합계는 항상 0입니다(이것은 뉴턴의 운동 제3법칙의 회전 유사).따라서 폐쇄형 시스템(순 외부 토크가 없는 경우)의 경우 시스템의 총 토크는 0이어야 하며, 이는 시스템의 총 각운동량이 일정함을 의미합니다.특정 상호작용에 대한 각운동량의 변화를 [3]회전이라고 부르기도 하지만, 이는 매우 드문 일입니다.회전은 임펄스의 각도 유사체이다.
고전역학의 정의
각속도와 마찬가지로, 물체의 각운동량에는 두 가지 특별한 유형이 있습니다: 스핀 각운동량은 물체의 질량 중심 주위의 각운동량인 반면, 궤도 각운동량은 선택된 회전 중심 주변의 각운동량입니다.지구는 태양 주위를 공전하는 성격의 궤도 각운동량과 극지축을 중심으로 매일 자전하는 성격의 회전각운동량을 가지고 있다.총 각운동량은 스핀과 궤도각 모멘타의 합이다.지구의 경우, 각운동량은 행성과 태양 사이에서 작지만 중요한 정도로 교환되기 때문에 가장 보존된 양은 태양계의 총 각운동량이다.점 입자의 궤도 각운동량 벡터는 항상 평행하고 궤도 각속도 벡터 θ에 정비례하며, 여기서 비례 상수는 입자의 질량과 원점으로부터의 거리에 좌우된다.강체의 스핀 각도 운동량 벡터는 비례하지만 스핀 각도 속도 벡터 δ와 항상 평행하지는 않으므로 비례 상수는 스칼라가 아닌 2차 텐서로 만든다.
2차원 궤도 각운동량
각운동량은 특정 축에 대한 물체의 회전 관성과 회전 속도(라디안/초)의 곱을 나타내는 벡터량(더 정확히는 의사벡터)입니다.그러나 입자의 궤적이 단일 평면에 있다면, 각운동량의 벡터 특성을 버리고 스칼라(더 정확히는 의사 스칼라)[4]로 취급하는 것으로 충분하다.각운동량은 선형운동량의 회전유사체로 간주할 수 있다.따라서 선형 운동량 p가 질량 m과 선형 속도 v에 비례할 때,
각운동량 L은 [5]관성 I의 모멘트 및 초당 라디안 단위로 측정된 각속도 θ에 비례한다.
물질의 양에만 의존하는 질량과 달리, 관성 모멘트는 또한 회전축의 위치와 물질의 모양에 따라 달라진다.원점 선택에 의존하지 않는 선형 속도와 달리 궤도 각 속도는 항상 고정된 원점에 대해 측정됩니다.따라서 엄밀히 말하면 L은 [6]그 중심에 상대적인 각운동량이라고 할 수 있다.
I 의경우 r 2m({ m}m 원형운동의 경우 r r r r {v이므로 각운동량은 r, {{ L =} {}, r} {frcd {fr로 확장할 수 있다.
회전 반지름 r과 p {\ p의 선형 모멘텀의 곱 여기서 v {\ }는 반지름에서 동등한 선형(접선 (= r\obe})입니다.
이 간단한 분석은 반지름 벡터에 수직인 움직임의 성분만 고려한다면 비원형 움직임에도 적용될 수 있다.그런 경우에는
서 v = v ( {\) { v_ } v)은 운동의 수직 성분이다.확장, m v ( ), {\ L(\)} 정렬, sin ( ) {\ L mv 축소 각운동량도 표현할 수 있습니다.
서 r \r _ { \ } \ ( \ )}은 모멘트 암의 길이이며, 원점에서 입자의 경로로 수직으로 떨어진 선입니다.운동량 모멘트가 [7]가리키는 것은 (모멘트 암의 길이)×(선형 운동량)의 정의입니다.
스칼라—라그랑주 역학의 각운동량
또 다른 접근법은 각운동량을 기계계의 라그랑지안으로 표현되는 각좌표(\의 공역운동량(표준운동량이라고도 함)으로 정의하는 것이다.m(\ m이 외력장이 없는 경우 a a의 원 안에서 움직이도록 구속된 기계 시스템을 고려합니다.시스템의 운동 에너지는
그리고 잠재적인 에너지는
그럼 라그랑지안은
일반화 운동량은 좌표(\에 "공역적으로" 작용한다.
3차원 궤도 각운동량
궤도 각운동량을 3차원으로 완전히 정의하려면 위치 벡터가 각을 쓸어내는 속도, 각도 변위의 순간 평면에 수직인 방향 및 관련된 질량과 [8]이 질량이 우주에서 어떻게 분포되는지 알아야 한다.이 각운동량의 벡터 특성을 유지함으로써 방정식의 일반적인 특성도 유지되며, 회전 중심에 대한 모든 종류의 3차원 운동(원형, 선형 또는 기타)을 설명할 수 있습니다.벡터 표기법에서 원점을 중심으로 움직이는 점 입자의 궤도 각운동량은 다음과 같이 표현될 수 있다.
어디에
- m {\ I은 점 질량에 대한 관성 모멘트입니다.
- × r {display {}})=2}})는 원점에 대한 입자의 궤도 각속도이다.
- {\은는) 원점에 대한 입자의 위치 입니다. r {\ r=\ \
- 는원점에 대한 입자의 선형 속도입니다.
- m은 입자의 질량입니다.
이는 확장, 축소될 수 있으며 벡터 대수의 규칙에 따라 재배열될 수 있습니다.
이는 의 위치 벡터r \ {r와) 선형 p \=의 교차곱이다.교차곱의 정의에 따르면 \벡터는 r과 p둘 에 수직이며, 각속도는 다음과 같이 각변위 평면에 수직이다.벡터의 선두에서 반시계방향으로 이동합니다.로 L\ 벡터는 r및 가 평면을 정의합니다.
단위 u {\을 각도 변위 평면에 수직으로 정의하면 스칼라 각도 속도 {\가 됩니다.
- ^ = {\ 、 { \ \{ { u= sysysy symbmbmb
- , \opha ={v_}}{ 여기서 v {\v_{\}}는 위와 같이 동작의 수직 성분입니다.
따라서 이전 섹션의 2차원 스칼라 방정식은 방향을 지정할 수 있습니다.
L v {\이며, 여기서 모든 움직임은 r {\ r에 수직입니다.
구면 좌표계에서 각운동량 벡터는 다음과 같이 표현된다.
임의의 치수에서의 각운동량
이 섹션은 확장해야 합니다.추가해서 도와주시면 됩니다. (2021년 6월) |
교차곱을 사용하여 각운동량을 정의하는 것은 3차원에만 적용됩니다.이를 바이벡터 L = r µ p로 정의하는 것은 임의의 차원에서 유효하다.
선형 운동량과 유사
각운동량은 선형운동량의 회전유사체로 설명할 수 있다.선형 운동량과 마찬가지로 질량과 변위 요소를 포함합니다.선형 운동량과 달리 위치 및 형상 요소도 포함합니다.
물리학의 많은 문제들은 움직이는 물질이 그 점에 어떤 영향을 미치는지 알기를 원하는 장소, 즉 그 점에 대한 실제 회전 중이든 아니면 단순히 지나쳐 가든지 간에, 물질의 움직임을 수반합니다. 즉, 움직이는 물질이 그 점에 어떤 영향을 미치는지 알기를 바랍니다.-그것에 에너지를 가하거나 그것에 대한 작업을 수행할 수 있을까요?에너지, 즉 작업을 수행할 수 있는 능력은 물질의 관성과 변위를 조합하여 물질에 에너지를 저장할 수 있습니다.관성은 질량에 의해 측정되고 변위는 속도에 의해 측정됩니다.그들의 제품은,
문제의 [9]모멘텀입니다.이 모멘텀을 중심점으로 참조하면 모멘텀이 해당 포인트에 직접 적용되지 않는다는 복잡한 문제가 발생합니다.예를 들어 바퀴의 바깥쪽 가장자리에 있는 물질의 입자는 실질적으로 바퀴의 반경과 같은 길이의 레버 끝에 있으며, 그 운동량은 레버를 중심점 중심으로 회전시킨다.이 가상의 레버는 모멘트 암이라고 알려져 있습니다.이것은 모멘트로 알려진 효과인 모멘트의 길이에 비례하여 운동량의 힘을 곱하는 효과가 있습니다.따라서 입자의 운동량은 특정 지점을 가리킵니다.
여기서 말하는 것처럼 입자의 운동 모멘트와 그 특정 중심점의 운동 모멘트를 각운동량이라고 합니다. v { Lrmv }는 모멘트(m { m} 회전 암 { r와 선형(직선 등가) { v를 결합한 것입니다. 중심점을 가리키는 선형 속도는 단순히 r{ r의 곱입니다.ngular speed \ \ obega、 \ v r \ 、 moment moment moment moment moment moment moment ng 。따라서 각운동량은 m .\ L =obega . } 약간 하면 L m, \ L= r m \ }의 양 r { r m} m은 입자의 관성 모멘트이며, 때로는 제2 모멘트라고도 불린다.이것은 회전 [10]관성의 척도입니다.
위의 번역 모멘텀과 회전 모멘텀은 벡터 형식으로 나타낼 수 [citation needed]있습니다.
v \= 선형운동
{ \{ } ={\ 회전용
운동량의 방향은 직선 이동의 속도 방향과 관련이 있습니다.각운동량의 방향은 회전의 각속도와 관련이 있다.
관성모멘트는 스핀각운동량의 중요한 부분이기 때문에 후자는 반드시 전자의 모든 합병증을 포함하며,[11] 이는 질량의 기본 비트에 회전중심으로부터의 거리의 제곱을 곱하여 계산됩니다.따라서 전체 관성 모멘트 및 각운동량은 회전 중심과 다양한 비트에 대한 회전 방향의 물질 구성에 대한 복잡한 함수입니다.
예를 들어 바퀴나 소행성 같은 강체의 경우, 회전 방향은 단순히 회전 축의 위치 대 물체의 물질입니다.질량의 중심을 통과할 수도 있고 통과하지 않을 수도 있고 완전히 몸 밖에 있을 수도 있습니다.동일한 물체에 대해 각 운동량은 회전이 [12]일어날 수 있는 모든 가능한 축에 대해 다른 값을 가질 수 있습니다.축이 [13]질량 중심을 통과할 때 최소값에 도달합니다.
중심 주위를 회전하는 물체 집합의 경우, 예를 들어 태양계의 모든 본체와 같이, 방향은 대부분의 본체의 축이 시스템의 축에 가깝게 놓여 있는 태양계와 같이 어느 정도 정리되어 있을 수 있습니다.방향은 완전히 무작위일 수도 있습니다.
간단히 말해, 질량이 많고 회전 중심에서 멀수록(모멘트 암이 길수록), 관성 모멘트가 커지며, 따라서 주어진 각 속도에 대한 각 운동량이 커집니다.많은 경우 관성 모멘트, 즉 각운동량은 다음과 같이 [14]단순화할 수 있습니다.
- 서 k{\k}는 회전 반지름으로 전체 m {\ m이 집중된 것으로 간주될 수 있는 축으로부터의 거리입니다.
로 점 m의 관성 모멘트는 다음과 같이 정의된다.
- 서 rr은 회전 중심에서 본 점 질량의 반지름입니다.
그리고 모든 집합 })에 대해 합계를 구한다.
각운동량의 위치와 형태에 대한 의존성은 단위 대 선형운동량에 반영됩니다. 각운동량의 경우 kgµm2/s 또는 Nµmµs, 선형운동량의 경우 kgµm/s 또는 Nµs입니다.관성 모멘트의 곱에 각속도를 곱한 각운동량을 계산할 때, 각속도는 초당 라디안으로 표현되어야 하며, 여기서 라디안은 단일성의 무차원 값을 가정한다.(치수 분석을 수행할 때 라디안을 기본 단위로 취급하는 방향 분석을 사용하는 것이 생산적일 수 있지만 국제 단위 시스템에서는 그렇지 않습니다.)각운동량의 단위는 토크시간으로 해석할 수 있습니다.각운동량이 LNµs인 물체는 LNµs의 [15][16]각임펄스에 의해 0의 각속도로 저감할 수 있다.
각운동량의 축에 수직이고 질량의 중심을[17] 통과하는 평면은 때때로 불변 평면이라고 불리는데, 이는 외부의 영향으로부터 자유로운 시스템 내 물체의 상호작용만 [18]고려한다면 축의 방향이 고정된 상태로 유지되기 때문이다.그러한 평면 중 하나가 태양계의 불변 평면이다.
각운동량 및 토크
뉴턴의 운동 제2법칙은 수학적으로 표현될 수 있다.
또는 힘 = 질량 × 가속.점 입자의 회전 등가는 다음과 같이 도출할 수 있습니다.
즉, 토크(즉, 각운동량의 시간 미분)는
관성 모멘트는 m 2 mr이므로 t r d p(\ style 가 됩니다.}}= t d d + r , { \{ { } { } {\{{ {\로 환원됩니다.
이것은 뉴턴의 제2법칙의 회전 유사체이다.토크가 반드시 각도 가속도에 비례하거나 평행할 필요는 없습니다(예상대로).그 이유는 입자의 관성 모멘트가 시간에 따라 변할 수 있기 때문인데, 이것은 일반적인 질량으로는 일어날 수 없는 일이다.
각운동량 보존
일반적인 고려 사항
뉴턴의 운동 제3법칙의 회전유사체는 "폐쇄 시스템에서는 어떤 물질에도 동일한 [19]축에 대해 등가 토크를 가하지 않고는 어떠한 토크를 가할 수 없다"고 쓰여 있을 것이다.따라서 닫힌 시스템의 물체 간에 각운동량을 교환할 수 있지만 교환 전후의 총각운동량은 일정하게 유지됩니다(보존).[20]
다른 방법으로 보면, 뉴턴의 운동 제1법칙의 회전 유사체는 "강체는 외부의 [19]영향에 의해 작용하지 않는 한 균일한 회전 상태로 계속된다"고 쓰여질 수 있다.따라서 외부의 영향을 받지 않고 시스템의 원래 각운동량은 [21]일정하게 유지됩니다.
각운동량 보존은 중심력 운동을 분석하는 데 사용된다.어떤 물체에 대한 순 힘이 항상 어떤 점, 즉 중심을 향한다면, 모든 힘이 반지름 벡터를 따라 향하고 반지름에 수직인 것이 없기 때문에 중심에 대한 토크는 물체에 없다.수학적으로 토크 × , {\ =\=\ 은(는) 병렬 벡터입니다. 이 r{\{ 및F은) 병렬 벡터입니다.따라서 중심 주위의 물체의 각운동량은 일정합니다.행성이나 위성의 궤도에서의 중력은 항상 주체를 향해 있고 공전하는 물체는 주체를 따라 이동할 때 거리와 속도를 교환함으로써 각운동량을 보존하는 경우이다.중심력 운동은 원자의 Bohr 모델 분석에도 사용됩니다.
행성의 경우, 각운동량은 행성의 회전과 공전 사이에 분포되어 있으며, 이것들은 종종 다양한 메커니즘에 의해 교환된다.지구-달 시스템에서 각운동량이 보존되면 달이 지구에 가하는 조석토크로 인해 각운동량이 지구에서 달로 전달된다.이는 지구의 자전 속도가 하루에 [22]약 65.7나노초로 느려지고 달의 궤도 반경이 연간 [23]약 3.82센티미터로 점차 증가하는 결과를 초래한다.
각운동량 보존은 빙상 선수가 팔과 다리를 수직 회전축에 가깝게 할 때의 각가속도를 설명한다.체질량의 일부를 축에 가깝게 함으로써, 그녀는 몸의 관성 모멘트를 줄인다.각운동량은 관성모멘트와 각속도의 산물이기 때문에 각운동량이 일정하게 유지(보존)되면 스케이트 선수의 각속도(회전속도)가 증가해야 한다.
같은 현상은 작고 작은 별들이 훨씬 더 크고 느리게 회전하는 별들로 형성될 때 매우 빠른 회전 속도를 발생시킵니다.
보존이 시스템의 역학에 대한 완전한 설명은 아니지만 중요한 제약사항입니다.예를 들어 회전하는 팽이는 중력 토크의 영향을 받아 회전축 주위의 각운동량을 변화시키지만 회전 접촉점의 마찰을 무시하여 회전축의 각운동량을 보존하고 세차축의 각운동량을 보존한다.또한, 어떤 행성계에서도, 행성, 별, 혜성, 그리고 소행성은 모두 수많은 복잡한 방식으로 움직일 수 있지만, 시스템의 각 운동량이 보존되기 위해서만 가능합니다.
노에터의 정리는 모든 보존 법칙이 기초 물리학의 대칭(불변)과 연관되어 있다고 말한다.각운동량 보존과 관련된 대칭은 회전 불변성이다.한 축을 중심으로 어떤 각도로 회전하더라도 시스템의 물리학적 특성이 변하지 않는다는 사실은 각운동량이 [24]보존된다는 것을 의미한다.
뉴턴의 운동 제2법칙과의 관계
각운동량 총보존은 회전하 대칭계의 노에터의 정리에서 비롯된 뉴턴의 운동법칙과는 별도로 이해될 수 있지만, 또한 단순히 뉴턴의 제2법칙에서 직접 도달할 수 있는 결과를 계산하는 효율적인 방법으로도 이해될 수 있다.자연의 힘(뉴턴의 제3법칙, 맥스웰 방정식, 로렌츠 힘 등)을 지우는 것.사실, 모든 점의 위치와 속도의 초기 조건과 그러한 조건에서의 힘을 고려할 때, 뉴턴의 제2법칙을 사용하여 위치의 제2도함수를 계산할 수 있으며, 이를 푸는 것은 시간에 [25]따른 물리적 시스템의 발달에 대한 완전한 정보를 제공한다.하지만, 이것은 입자 스핀의 존재 때문에 양자 역학에서는 더 이상 사실이 아니라는 것을 주목하라. 입자 스핀은 우주에서의 점 같은 운동의 누적 효과로는 설명할 수 없는 각 운동량이다.
예를 들어, 피겨 스케이터가 손을 잡고 원형 운동을 가속할 때 관성 모멘트를 줄이는 것을 고려해 보자.각운동량 보존의 관점에서 각운동량 L의 경우 관성모멘트 I와 각속도 θ가 있다.
이를 통해 변경에 필요한 에너지는 다음과 같습니다.
따라서 관성 모멘트의 감소는 에너지를 투자해야 합니다.
이것은 뉴턴의 법칙을 사용하여 계산된 작업과 비교할 수 있습니다.회전하는 본체의 각 점은 각 시점에서 다음과 같은 반경 가속도로 가속됩니다.
운동 중심에 상대적인 위치 벡터가 주어진 시점에서 z축에 수직이고 거리 z에 있는 질량 m의 점을 관찰해 봅시다.이 점에 대한 구심력은 원형 운동을 유지하며 다음과 같다.
따라서 이 지점을 이동 중심에서 더 먼 거리 dz로 이동하기 위해 필요한 작업은 다음과 같습니다.
점 유사하지 않은 물체의 경우 m을 단위 z당 질량 밀도로 대체하여 이 위에 통합해야 합니다.그 결과, 다음과 같이 됩니다.
각운동량을 보존하는 데 필요한 에너지입니다.
위의 계산은 운동학만 사용하여 질량당 수행할 수 있습니다.따라서 피겨 스케이터가 손을 안으로 당기면서 접선 속도를 가속하는 현상은 일반인의 언어로 다음과 같이 이해할 수 있다.스케이트 선수의 손바닥은 일직선이 아니기 때문에 안쪽으로 계속 가속하고 있지만, 안쪽으로의 움직임이 0일 때 가속이 이루어지기 때문에 추가 속도가 붙지는 않는다.그러나 손바닥을 몸에 더 가까이 당기는 경우에는 다릅니다.이제 회전으로 인한 가속도가 속도를 증가시키지만 회전으로 인해 속도가 증가하면 안쪽으로 상당한 속도로 변환되지 않고 회전 속도가 증가합니다.
라그랑주 형식주의에서
라그랑주 역학에서, 주어진 축을 중심으로 회전하는 각운동량은 같은 축을 중심으로 한 각도의 일반화 좌표의 공역운동량이다.예를 들어, Z 축 주위의 각 인 Lz {\는 다음과 같습니다.
서 L {L은 라그랑지안이고 z(\는 z축 주위의 각도입니다.
각도의 시간 도함수인 z { style }}는 각속도 z { _입니다. 일반적으로 라그랑지안은 운동에너지를 통한 각속도에 의존합니다.후자는 z축 주위의 x-y 평면의 접선 부분이 다음과 같도록 반경 및 접선 부분까지의 속도를 분리하여 작성할 수 있습니다.
여기서 첨자 i는 i번째 본체를 나타내고 mT, v, θ는z z축 주위의 질량, 접선 속도 및 해당 축 주위의 각 속도를 각각 나타냅니다.
점처럼 보이지 않고 밀도 θ를 가진 물체의 경우 대신 다음과 같은 것이 있습니다.
여기서 통합은 [26]신체 영역 전체에 걸쳐 진행되며z I는 z축 주위의 관성 모멘트입니다.
따라서 잠재적 에너지가 δ에z 의존하지 않는다고 가정하면(전자파 시스템의 경우 이 가정이 실패할 수 있음), ith 물체의 각 운동량을 알 수 있다.
지금까지 각 물체를 별도의 각도로 회전시켰습니다. 또한 전체 시스템을 회전시키는 전체 각도 θ를z 정의할 수 있습니다. 따라서 각 물체는 z축을 중심으로 회전하며 전체 각도 운동량을 가질 수 있습니다.
오일러-라그랑주 방정식으로부터 다음과 같이 된다.
라그랑지안은 전위를 통해서만 물체의 각도에 의존하기 때문에 다음과 같은 조건이 있습니다.
이 값은 ih 물체의 토크입니다.
그래서는 잠재력이 전반적인 회전의 각도 θz(따라서 물체의 각도에 대한 이견을 통해서만 형태로 V(θ ziθ zj 달려 있을 것))V({\displaystyle V({\theta_{z}}_{나는},{\theta_{z}에 의해}무관한 것을 시스템 회전에, 불변이다_{j. 가정하자}따라서 총 각운동량을 구합니다.
따라서 z축 주위의 각운동량이 보존됩니다.
이 분석은 각 축별로 개별적으로 반복하여 각운동량 벡터에 대한 대화를 제공한다.그러나 세 축 주위의 각도는 독립적이지 않기 때문에 동시에 일반화 좌표로 취급할 수 없습니다. 특히 각 점당 두 개의 각도로 위치를 결정할 수 있습니다.강체의 경우, 완전한 기술을 위해서는 3개의 변환 자유도와 더불어 3개의 회전 자유도의 지정이 요구되지만, 이것들은 데카르트 축을 중심으로 한 회전으로 정의될 수 없다(오일러 각도 참조).이 경고는 각운동량 연산자의 다른 구성요소의 사소한 정류 관계에서 양자 역학에 반영된다.
해밀턴식 형식주의에서
마찬가지로, 해밀턴 역학에서는 해밀턴을 각운동량의 함수로 설명할 수 있다.이전과 같이 ih 물체에 대한 z축 주위의 회전과 관련된 운동 에너지 부분은 다음과 같다.
이는 z축을 따라 운동량에 대한 에너지 의존 p {{}}_i}}}}와 유사하다.
해밀턴 방정식은 z축 주위의 각도를 같은 축 주위의 각 운동량인 공역 운동량과 관련짓습니다.
첫 번째 방정식은 다음과 같다.
그래서 우리는 라그랑주 형식주의와 같은 결과를 얻습니다.
모든 축을 조합하는 경우 운동 에너지는 다음과 같이 기술합니다.
여기서r p는 반경 방향의 운동량이고 관성 모멘트는 3차원 매트릭스입니다. 굵은 글씨는 3차원 벡터를 나타냅니다.
포인트형 바디에는 다음과 같은 기능이 있습니다.
해밀턴의 운동 에너지 부분의 이러한 형태는 중심 전위 문제를 분석하는 데 유용하며, 양자 역학 작업 프레임(예: 수소 원자 문제)으로 쉽게 변환됩니다.
궤도역학에서의 각운동량
고전 역학에서 각운동량 언어는 뉴턴의 운동 법칙으로 대체될 수 있지만, 이것은 태양계의 행성 운동과 같은 중심 전위에서의 운동에 특히 유용합니다.따라서, 태양계에서 행성의 궤도는 그것의 에너지, 각운동량 그리고 좌표 프레임에 상대적인 궤도 장축의 각도에 의해 정의된다.
천체역학 및 천체역학에서, 각운동량과 밀접하게 관련된 양은 다음과 같이 정의된다[27].
특정 각운동량이라고 합니다.L h. { { } = .} 질량은 종종 궤도 역학 계산에서 중요하지 . 왜냐하면 물체의 운동은 중력에 의해 결정되기 때문이다.시스템의 주요 물체는 종종 움직이는 어떤 물체보다 훨씬 더 커서 작은 물체에 대한 중력 효과가 무시될 수 있습니다; 그것은 사실상 일정한 속도를 유지합니다.모든 물체의 운동은 질량에 관계없이 같은 방식으로 중력의 영향을 받고, 따라서 모든 물체는 같은 조건에서 거의 같은 방식으로 움직인다.
입체
각운동량은 또한 자이로스코프나 암석행성과 같은 회전하는 강체를 설명하는 데 매우 유용한 개념이다.밀도함수 θ(r)를 갖는 연속질량분포에서 질량내 위치벡터 r을 갖는 미분용적요소 dV는 질량요소 dm=θ(r)dV를 가진다.따라서 이 원소의 극소 각운동량은 다음과 같습니다.
그리고 이 차이를 전체 질량의 부피에 걸쳐 적분하면 전체 각운동량이 산출됩니다.
다음 유도에서 이와 유사한 적분은 연속 질량의 경우 합계를 대체할 수 있다.
입자의 포집
임의의 기원에 대해 움직이는 입자의 집합은 각운동량의 방정식을 발전시키는 데 도움이 됩니다.각운동량의 움직임을 자신의 질량 중심과 원점에 대한 구성요소로 분해하여 발전시키는 것이 좋습니다.정해진,
- { _ {는 i의 질량입니다.
- 인 입자 i(원점의 위치 벡터입니다.
- _{는 원점을 포함한입자의 속도이다.
- 은 원점을 포함한 질량 중심 위치 벡터입니다.
- 는 원점을 포함한 질량 중심의 속도이다.
- ir} _는 질량 중심을 갖는 입자(\ i의 위치 벡터입니다.
- i \ \{ } { i}는 질량의 중심을 갖는 의 속도이다.
입자의 총 질량은 단순히 입자의 총합일 뿐이고
질량 중심의 위치 벡터는 다음과 [28]같이 정의된다.
검사 결과,
- i + {\i}=\+\ {} i + { \ {V} +\ {i}.
입자 집합의 총 각운동량은 각 입자의 각운동량의 합이다.
R × i) { {} = \ _(\times } } (1)
R확장하는 것 나는}, _{나는}{\displaystyle \mathbf{R}.
V를 넓히는 일 나는}, _{나는}{\displaystyle \mathbf{V}.
그것은(사이드 바를 참조하십시오), 표시할 수 있다.
| 는 증명하다.
어떤 질량의 중심의 정의에 의해는 0,{\displaystyle \mathbf{0},}와 비슷하게 ∑에 나는 비에이라는 나는 v.{\displaystyle \sum_{나는}m_{나는}\mathbf{v}_{나는}.} |
- r { \ _ { i _ { i } \r}_ { i }} i i i i i i m m i v , \ \{ i } m _ { } { \{ 0} ,
따라서 두 번째 항과 세 번째 항은 사라집니다.
첫 번째 항은 재배치할 수 있고
입자의 [29]총 각운동량은 최종적으로
× V + i × i {\ =\ M _}\ \ {v} {v} {i
첫 번째 항은 원점에 대한 질량 중심의 각 운동량입니다.① 단입자와 마찬가지로 아래는 속도 V로 이동하는 질량 중심에서 M질량 1개 입자의 각운동량이다.두 번째 항은 질량 중심을 기준으로 움직이는 입자의 각 운동량으로, 아래의 below 고정 질량 중심과 유사합니다.결과는 일반적입니다. 입자의 움직임은 원점이나 질량의 중심을 중심으로 회전하거나 회전하는 데 제한되지 않습니다.입자는 개별 질량일 필요는 없지만 고체 등 연속 분포의 요소가 될 수 있습니다.
방정식 (2)를 벡터 아이덴티티로 재배치하고, 두 용어에 "하나"를 곱하고, 적절하게 그룹화한다.
모멘트 I I와 각속도(\의 관점에서 입자계의 총 각운동량을 나타낸다.
}} (3)
단입자 케이스
단일 입자가 임의의 원점 주위를 이동하는 경우,
질량중심이 고정된 경우
원점과 관련하여 공간에 고정된 질량의 중심의 경우,
- R R , {\ {\oboldsymbol {\ 및 식 (2)와 (3)은 다음과 같이 감소한다.
일반상대성이론의 각운동량
현대(20세기) 이론 물리학에서 각운동량(내재적인 각운동량 제외 – 아래 참조)은 고전적인 의사벡터 대신 다른 형식주의를 사용하여 기술된다.이 형식주의에서 각운동량은 회전 불변성과 관련된 2-형태 노에테르 전하이다.그 결과, 점근적으로 회전 불변하지 않는 [citation needed]한, 일반적인 곡면 시공간에서는 각운동량이 보존되지 않는다.
고전 역학에서 입자의 각운동량은 평면 요소로 재해석될 수 있습니다.
(이 제품들은 유사한 특성을 가지지만 2가치가 없다) 외부 곱 have이 교차 곱 ×을 대체한다.이는 x 및 p 벡터로 정의되는 평면 요소로서 보다 명확한 기하학적 해석을 할 수 있다는 장점이 있으며, 식은 임의의 수의 차원(2개 이상)에서 참입니다.데카르트 좌표:
또는 인덱스 표기법에서 보다 간결하게:
각속도는 성분 θ를ij 갖는 대칭 2차 텐서로 정의할 수도 있다.두 개의 반대칭 텐서 사이의 관계는 이제 4차 [30]텐서가 되어야 하는 관성 모멘트에 의해 제공됩니다.
다시 말하지만 텐서로서의 L과 δ의 방정식은 모든 차원에 대해 참입니다.이 방정식은 L과 θ가 쌍대수이고 관성 모멘트가 그들 사이의 매핑인 기하학적 대수 형식론에서도 나타난다.
상대론적 역학에서 입자의 상대론적 각운동량은 2차 반대칭 텐서로 표현된다.
4 벡터의 언어, 즉 4개의 위치 X와 4개의 운동량 P로 표현하며 입자의 질량 중심 운동과 함께 위의 L을 흡수한다.
위의 경우 각각, 입자 계통의 경우, 총 각운동량은 개별 입자 각 모멘타의 합일 뿐이며, 질량 중심은 계통의 것이다.
양자역학에서의 각운동량
양자역학에서 각운동량은 (다른 양들과 마찬가지로) 연산자로 표현되며, 그 1차원 투영법은 양자화된 고유값을 가지고 있다.각운동량은 하이젠베르크 불확도 원리에 따라 결정되며, 이는 항상 하나의 투영("성분"이라고도 함)만 일정한 정밀도로 측정할 수 있음을 의미하며, 나머지 두 개는 불확실한 상태로 유지됩니다.이로 인해 양자 입자의 회전축이 정의되지 않는다.양자 입자는 "spin"이라고 불리는 비궤도 각 운동량을 가지고 있지만, 이 각 운동량은 회전 [31]운동과 일치하지 않습니다.상대론적 양자역학에서 위의 상대론적 정의는 장력 연산자가 된다.
스핀, 궤도 및 총 각운동량
r을 양자 위치 연산자로, p를 양자 운동량 연산자로 재해석하여 Lr × p \{L=\ \times \mathbf {p 로 각 운동량의 고전적 정의를 양자 역학으로 옮길 수 있다.L은 연산자로, 구체적으로는 궤도 각운동량 연산자로 불린다.각운동량 연산자의 성분은 Lie 대수의 정류 관계를 충족하므로 (3).실제로, 이러한 연산자는 정확히 양자 힐버트 [33]공간에서의 회전 그룹의 극소량 작용이다.(아래 각운동량 연산자에 대한 설명도 회전 발생기로 참조하십시오.)
하지만, 양자 물리학에서는 스핀 연산자 S에 의해 표현되는 스핀 각 운동량이라고 불리는 다른 형태의 각 운동량이 있다. 스핀은 종종 문자 그대로 한 축을 중심으로 회전하는 입자로 묘사되지만, 이것은 오해의 소지가 있고 부정확한 그림이다: 스핀은 공간에서의 어떤 운동과 관계없는 입자의 본질적인 특성이다.궤도 각운동량과 근본적으로 다르다.모든 소립자는 특징적인 스핀(아마도 0)[34]을 가지며, 거의 모든 소립자는 0이 아닌 [35]스핀을 가진다.예를 들어 전자는 스핀 1/2(실제로는 스핀 θ/2를 의미), 광자는 스핀 1(실제로는 스핀 θ를 의미), 파이-메손은 [36]스핀 0을 가진다.
마지막으로 모든 입자와 필드의 스핀과 궤도 각운동량을 모두 합친 총각운동량 J가 있다(한 입자에 대해 J = L + S).각운동량 보존은 J에는 적용되지만 L이나 S에는 적용되지 않는다. 예를 들어 스핀-오빗 상호작용을 통해 각운동량이 L과 S 사이를 왔다 갔다 하면서 총이 일정하게 유지된다.전자와 광자는 총 각운동량에 대한 정수 기반 값을 가질 필요는 없지만 반정수 [37]값을 가질 수도 있습니다.
분자에서 총 각운동량 F는 회전각운동량 N, 전자 스핀각운동량 S 및 핵 스핀각운동량 I의 합이다.전자 싱글트 상태의 경우, Rovibronic 각운동량은 N이 아니라 J로 표시됩니다. Van [38]Vleck에 의해 설명되었듯이, 분자 고정축이라고 하는 분자 회전 운동량의 구성요소는 공간 고정축에 관한 구성요소와 다른 정류 관계를 가집니다.
양자화
양자역학에서 각운동량은 양자화된다.즉, 연속적으로 변화할 수 없고, 특정 허용값 사이의 "양자 도약"에서만 가능하다.모든 시스템에 대해 다음과 같은 측정 결과에 대한 제한이 적용됩니다. 여기서(\는 플랑크 이고 n^(\은 x, y 또는 z와 같은 유클리드 벡터입니다.
| 재보면... | 결과는... |
| n { S _ { \ { } J { \ displaystyle J _ { \ { } } | |
| 2 (n + ) left [ \ 2 n ( +) \ right 。서 , 1,} | |
| S J | (n + ) [ \ ( + 1)\ right 。 , 1 , , , . { , 1 , \ |
플랑크 상수(\는 일상기준으로 10Js 정도로−34 작기 때문에 거시적 물체의 각운동량에 큰 영향을 주지 않는다.하지만, 그것은 미시적인 세계에서는 매우 중요합니다.예를 들어 화학에서 전자껍질과 서브껍질의 구조는 각운동량의 양자화에 큰 영향을 받습니다.
각운동량의 양자화는 닐스 보어에 의해 원자 모형에서 처음 가정되었고 후에 에르빈 슈뢰딩거에 의해 슈뢰딩거 방정식에서 예측되었다.
불확실성
L × \{L} =\\times \{p에서 6개의 연산자가 관련된다.위치 x (\ (\ z (\displaystyle 및 모멘텀 x (\ p (\ 를 나타냅니다.단, pz (\displaystyledisplaystyle 의 불확정확실현상이 있습니다.단, p_{z}의 원리에 의해 알 수 없습니다.단,이 6가지 양을 모두 임의의 정밀도로 동시에 알 수 있는 것은 아닙니다.따라서 입자의 각운동량에 대해 알 수 있거나 측정할 수 있는 것에는 한계가 있습니다.한 축을 따라 각운동량 벡터의 크기와 성분을 동시에 측정하는 것이 최선의 방법인 것으로 밝혀졌다.
은 각운동량 의 여러 이 하지 않는 것과 밀접한 이 있습니다정확한 정류관계는 각운동량를 참조하십시오
회전 발생기로서의 총 각운동량
위에서 설명한 바와 같이 궤도 각운동량 L은 고전역학에서 다음과 정의된다: L × p\ =\ \ 그러나 총 각운동량 J는 "회전수"[39]로 정의된다.보다 구체적으로 J는 연산자가 다음과 같이 정의됩니다.
모든 시스템을에 대해 로 회전시키는 회전 연산자입니다 (수식의 "는 연산자 지수함수를 나타냅니다.)반대로 말하면, 우리의 양자 힐버트 공간이 무엇이든 간에, 우리는 회전군 SO(3)가 그것에 작용하기를 기대한다.다음으로 SO(3)의 라이 대수의 관련 작용이 있다. 힐버트 공간에 대한 SO(3)의 작용을 설명하는 연산자는 (총)각운동량 연산자이다.
각운동량 연산자와 회전 연산자 사이의 관계는 수학에서 리 대수와 리 군 사이의 관계와 동일합니다.각운동량과 회전 사이의 밀접한 관계는 물리 법칙이 회전 불변할 때마다 각운동량이 보존된다는 것을 증명하는 노에터의 정리에 반영된다.
전기역학에서의 각운동량
전자기장에서 하전 입자의 운동을 설명할 때 표준 운동량 P(이 시스템의 라그랑지안으로부터 도출)는 게이지 불변성이 아니다.따라서 표준 각운동량 L = r × P도 게이지 불변성이 아니다.대신 물리적인 운동량, 이른바 운동량(본 문서 전체에서 사용)은 (SI 단위)이다.
여기서 e는 입자의 전하이고 A는 전자기장의 자기 벡터 전위입니다.게이지 불변 각운동량, 즉 운동각운동량은 다음과 같이 주어진다.
양자역학과의 상호작용은 표준 정류관계에 관한 기사에서 더 자세히 논의된다.
광학에서의 각운동량
고전 맥스웰 전기역학에서 포인팅 벡터는 전자기장의 [40]선형 운동량 밀도입니다.
각운동량 밀도 L , , 은 고전 [41]역학에서와 같이 벡터 곱에 의해 주어진다.
위의 ID는 로컬로 유효합니다.즉, 주어진 t{r의 각 스페이스 r\displaystyle t
자연과 우주의 각운동량
열대성 사이클론 및 기타 관련 기상 현상은 역학을 설명하기 위해 각 운동량의 보존을 수반한다.바람은 주로 코리올리 효과로 인해 저기압 시스템을 중심으로 천천히 회전합니다.저압이 강해지고 천천히 순환하는 공기가 중앙으로 빨려들면 분자는 각운동량을 보존하기 위해 속도를 높여야 한다.그들이 중심에 도착할 때쯤에는 속도가 [42]파괴적이 된다.
요하네스 케플러는 운동량 보존에 대한 지식 없이 행성 운동의 법칙을 알아냈다.그러나 그가 발견한 지 얼마 되지 않아 각운동량 보존으로부터 그들의 유도가 결정되었다.행성들은 타원 궤도에서 더 멀리 있을수록 더 느리게 움직인다. 이것은 궤도 각운동량이 궤도의 반경에 비례한다는 사실로 직관적으로 설명된다.질량이 변하지 않고 각운동량이 보존되기 때문에 속도가 떨어진다.
조석 가속은 궤도를 도는 자연 위성(예: 달)과 그것이 공전하는 1차 행성(예: 지구) 사이의 조석력의 영향이다.달과 지구의 조석 팽대부 사이의 중력 토크는 달이 지속적으로 약간 더 높은 궤도로 추진되고 지구의 자전 속도가 느려지게 만든다.지구는 전체 각운동량이 보존되도록 달로 전달되는 각운동량을 잃는다.
엔지니어링 및 테크놀로지의 각운동량
각운동량 보존을 실용적으로 이용하는 예는 풍부하다.증기 엔진이나 내연 기관과 같은 엔진에서는 피스톤의 횡방향 운동을 회전 운동으로 효율적으로 변환하기 위해 플라이휠이 필요합니다.
관성 항법 시스템은 각운동량이 공간의 관성 프레임에 대해 보존된다는 사실을 명시적으로 사용한다.관성 항법은 극지방 만년설 아래에서 잠수함 여행을 가능하게 하는 것이지만, 현대 항해의 모든 형태에서 중요하다.
강선탄은 각운동량 보존으로 얻을 수 있는 안정성을 사용하여 궤도에 더 정확합니다.강선 총기와 대포의 발명은 전투에서 그들의 사용자에게 상당한 전략적 이점을 주었고, 따라서 역사의 기술적 전환점이 되었다.
역사
프린키피아에서 아이작 뉴턴은 운동 제1법칙의 예에서 각운동량을 암시했다.
응집력에 의한 부분이 항상 직선 운동으로부터 멀어지는 팽이는 공기에 의해 지연되는 경우를 제외하고는 회전을 멈추지 않습니다.더 많은 자유 공간에서 적은 저항으로 만나는 행성과 혜성의 큰 물체는 그들의 움직임을 훨씬 [43]더 오랜 시간 동안 진행적이고 원형으로 보존합니다.
그는 프린키피아에서 직접적으로 각운동량을 조사하지는 않았다.
이러한 종류의 반사로 인해 때때로 몸의 중심 주위에 원형운동이 일어난다.그러나 이것들은 내가 다음 사항에서 고려하지 않는 경우들이다; 그리고 이 [44]주제와 관련된 모든 특정한 것을 증명하는 것은 너무 지루할 것이다.
그러나, 면적 법칙에 대한 그의 기하학적 증명은 뉴턴의 천재성을 보여주는 뛰어난 사례이며, 중심력의 경우 각운동량 보존을 간접적으로 증명한다.
지역의 법칙
뉴턴의 유도
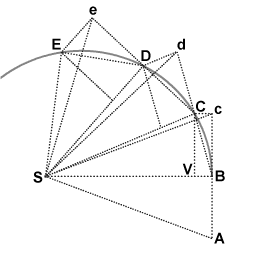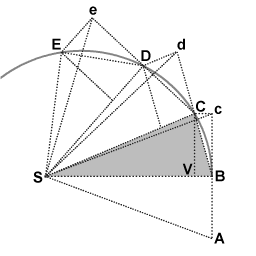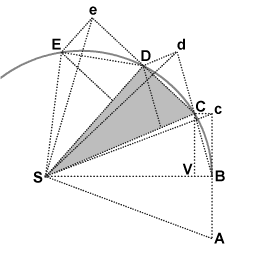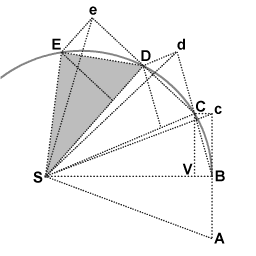
행성이 태양 주위를 돌 때, 태양과 행성 사이의 선은 동일한 시간 간격으로 동일한 영역을 쓸어냅니다.이것은 케플러가 행성운동의 두 번째 법칙을 설명했을 때부터 알려져 왔다.뉴턴은 독특한 기하학적 증거를 도출했고, 태양 중력의 매력적인 힘이 케플러의 모든 법칙의 원인이라는 것을 계속해서 보여주었다.
첫 번째 시간 간격 동안 물체는 A 지점에서 B 지점까지 이동한다.방해받지 않으면 두 번째 간격 동안 계속 c점을 찍습니다.오브젝트가 B에 도착하면 포인트S로 향하는 임펄스를 수신합니다.이 임펄스는 S를 향해 작은 속도를 더하여 이것이 유일한 속도라면 두 번째 간격 동안 B에서 V로 이동할 것이다.속도 구성의 법칙에 의해 이들 2개의 속도가 더해지고, 평행사변형 BcCV의 구성에 의해 점 C가 구해진다.따라서 객체의 경로는 임펄스에 의해 편향되어 두 번째 간격의 끝에 C 지점에 도착합니다.삼각형 SBc와 SBC는 밑변 SB가 같고 높이 Bc 또는 VC가 같기 때문에 면적이 같습니다.대칭에 의해 삼각형 SBc는 삼각형 SAB와 면적이 같기 때문에 오브젝트는 등시간 내에 등면적 SAB와 SBC를 소거한다.
포인트 C에서 오브젝트는 S에 대한 다른 임펄스를 수신하여 다시 세 번째 간격 동안 패스를 d에서 D로 꺾습니다.따라서 삼각형 SAB, SBc, SBC, SCd, SCD, SDe, SDE가 모두 동일한 면적을 갖는 E 이후까지 계속됩니다.시간 간격이 더 작아지면 ABCDE 경로는 연속 곡선에 무한히 근접합니다.
이 유도는 기하학적이며 특정한 힘이 가해지지 않기 때문에 케플러의 행성 운동 제2법칙보다 더 일반적인 법칙을 증명합니다.이는 면적 법칙이 모든 중심력, 유인력 또는 반발력, 연속력 또는 비연속력 또는 0에 적용됨을 보여준다.
면적법칙에서의 각운동량 보존
움직이는 물체에 의해 쓸려나간 영역에 대한 각운동량의 비례성은 삼각형의 밑면, 즉 S에서 물체에 이르는 선은 반지름과 동일하고 삼각형의 높이는 속도의 수직 구성요소에 비례한다는 것을 깨달음으로써 이해될 수 있습니다.만약 그 지역 단위 시간당 일대를 휩쓸고 따라서, 삼각 지역 공식 .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{에 의해 상수입니다.디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-onlyᆮ1(기지)(높이), 제품(기지)(높이)고 따라서 제품 rv⊥은 변함 없다:만약 r와 베이스 길이 있dec., v⊥와 높이Reased 비례적으로 늘려야 할 것이다.질량은 일정하기 때문에 각운동량은 거리와 속도의 교환에 의해 보존됩니다.
삼각 SBC의 경우 면적은 1/2(SB)(VC)와 같다.B에 가해지는 임펄스에 의해 최종적으로 C가 위치하는 경우, 제품(SB)(VC)은 일정하게 유지됩니다.마찬가지로 각 삼각형에 대해서도 마찬가지입니다.
뉴턴 이후
레온하르트 오일러, 다니엘 베르누이, 그리고 패트릭 다시는 모두 케플러의 행성 운동 제2법칙에 대한 분석의 결과인 면적 속도의 보존 측면에서 각운동량을 이해했다.그들이 일반적인 회전 [45]물질에 대한 의미를 깨닫지 못했을 것이다.
1736년, 뉴턴과 마찬가지로 오일러는 그의 기계에서 각운동량 방정식을 [46]더 이상 발전시키지 않고 일부에 대해 언급했다.
베르누이는 1744년 편지에서 "회전 운동의 순간"을 썼는데, 아마도 우리가 [47]현재 이해하고 있는 각운동량의 첫 개념일 것이다.
1799년, 피에르 시몬 라플라스는 고정 평면이 그의 불변 평면인 회전과 연관되어 있다는 것을 처음 깨달았다.
1803년 루이 포인소는 회전을 회전에 수직인 선분으로 표현하기 시작했고 "순간의 보존"에 대해 상세히 설명했다.
1852년 Léon Foucault는 지구의 자전을 보여주는 실험에 자이로스코프를 사용했다.
William J. M. Rankine의 1858년 응용역학 매뉴얼은 처음으로 각운동량을 현대적 의미로 정의했습니다.
길이가 각운동량의 크기에 비례하고 방향이 물체의 운동면 및 정점에 수직인 선으로, 물체의 운동을 선단으로부터 보았을 때 물체의 반지름-반경이 오른손으로 회전하는 것처럼 보이는 선.
같은 책의 1872년 판에서 랭킨은 "각운동량이라는 용어는 헤이워드 [48]씨가 도입했다"고 언급했는데, 아마도 R.B.를 언급했을 것이다.Hayward의 기사는 1856년에 도입되어 1864년에 발표된 Space with [49]Applications에서 어떤 방식으로든 움직일 수 있는 축에 관한 속도, 가속 및 모든 유사한 양을 추정하는 직접적인 방법에 관한 것입니다.랭킨은 18세기 말부터 19세기 [50]초까지 수많은 출판물에서 이 용어를 다루고 있기 때문에 틀렸다.그러나 Hayward의 기사는 영어권 국가에서 이 용어를 처음 사용한 것으로 보인다.이전에 각운동량은 일반적으로 영어로 "[51]회전하는 순간"이라고 불렸다.
「 」를 참조해 주세요.
각주
- ^ "Soaring Science: The Aerodynamics of Flying a Frisbee". Scientific American. August 9, 2012. Retrieved January 4, 2022.
- ^ "Tropical Cyclone Structure". National Weather Service. Retrieved January 4, 2022.
- ^ Moore, Thomas (2016). Six Ideas That Shaped Physics, Unit C: Conservation Laws Constrain Interactions (Third ed.). McGraw-Hill Education. p. 91. ISBN 978-0-07-351394-2.
- ^ Wilson, E. B. (1915). Linear Momentum, Kinetic Energy and Angular Momentum. The American Mathematical Monthly. Vol. XXII. Ginn and Co., Boston, in cooperation with University of Chicago, et al. p. 190 – via Google books.
- ^ Worthington, Arthur M. (1906). Dynamics of Rotation. Longmans, Green and Co., London. p. 21 – via Google books.
- ^ Taylor, John R. (2005). Classical Mechanics. University Science Books, Mill Valley, CA. p. 90. ISBN 978-1-891389-22-1.
- ^ Dadourian, H. M. (1913). Analytical Mechanics for Students of Physics and Engineering. D. Van Nostrand Company, New York. p. 266 – via Google books.
- ^ Watson, W. (1912). General Physics. Longmans, Green and Co., New York. p. 33 – via Google books.
- ^ Barker, George F. (1893). Physics: Advanced Course (4th ed.). Henry Holt and Company, New York. p. 66 – via Google Books.
- ^ Barker, George F. (1893). Physics: Advanced Course (4th ed.). Henry Holt and Company, New York. pp. 67–68 – via Google Books.
- ^ Oberg, Erik; et al. (2000). Machinery's Handbook (26th ed.). Industrial Press, Inc., New York. p. 143. ISBN 978-0-8311-2625-4.
- ^ Watson, W. (1912). General Physics. Longmans, Green and Co., New York. p. 34 – via Google books.
- ^ Kent, William (1916). The Mechanical Engineers' Pocket Book (9th ed.). John Wiley and Sons, Inc., New York. p. 517 – via Google books.
- ^ Oberg, Erik; et al. (2000). Machinery's Handbook (26th ed.). Industrial Press, Inc., New York. p. 146. ISBN 978-0-8311-2625-4.
- ^ Oberg, Erik; et al. (2000). Machinery's Handbook (26th ed.). Industrial Press, Inc., New York. pp. 161–162. ISBN 978-0-8311-2625-4.
- ^ Kent, William (1916). The Mechanical Engineers' Pocket Book (9th ed.). John Wiley and Sons, Inc., New York. p. 527 – via Google books.
- ^ Battin, Richard H. (1999). An Introduction to the Mathematics and Methods of Astrodynamics, Revised Edition. American Institute of Aeronautics and Astronautics, Inc. ISBN 978-1-56347-342-5., 페이지 97
- ^ Rankine, W. J. M. (1872). A Manual of Applied Mechanics (6th ed.). Charles Griffin and Company, London. p. 507 – via Google books.
- ^ a b Crew, Henry (1908). The Principles of Mechanics: For Students of Physics and Engineering. Longmans, Green, and Company, New York. p. 88 – via Google books.
- ^ Worthington, Arthur M. (1906). Dynamics of Rotation. Longmans, Green and Co., London. p. 82 – via Google books.
- ^ Worthington, Arthur M. (1906). Dynamics of Rotation. Longmans, Green and Co., London. p. 11 – via Google books.
- ^ Stephenson, F. R.; Morrison, L. V.; Whitrow, G. J. (1984). "Long-term changes in the rotation of the earth – 700 B.C. to A.D. 1980". Philosophical Transactions of the Royal Society. 313 (1524): 47–70. Bibcode:1984RSPTA.313...47S. doi:10.1098/rsta.1984.0082. S2CID 120566848. +2.40밀리초/세기 나누기 36525일
- ^ Dickey, J. O.; et al. (1994). "Lunar Laser Ranging: A Continuing Legacy of the Apollo Program" (PDF). Science. 265 (5171): 482–90, see 486. Bibcode:1994Sci...265..482D. doi:10.1126/science.265.5171.482. PMID 17781305. S2CID 10157934.
- ^ Landau, L. D.; Lifshitz, E. M. (1995). The classical theory of fields. Course of Theoretical Physics. Oxford, Butterworth–Heinemann. ISBN 978-0-7506-2768-9.
- ^ 테네바움, M. & 폴라드, H. (1985년)초등 수학 교과서의 상미분 방정식.엔지니어링과 과학.
- ^ David Morin (2008). Introduction to Classical Mechanics: With Problems and Solutions. Cambridge University Press. p. 311. ISBN 978-1-139-46837-4. 311페이지 발췌
- ^ Battin, Richard H. (1999). An Introduction to the Mathematics and Methods of Astrodynamics, Revised Edition. American Institute of Aeronautics and Astronautics, Inc. p. 115. ISBN 978-1-56347-342-5.
- ^ Wilson, E. B. (1915). Linear Momentum, Kinetic Energy and Angular Momentum. The American Mathematical Monthly. Vol. XXII. Ginn and Co., Boston, in cooperation with University of Chicago, et al. p. 188, equation (3) – via Google books.
- ^ Wilson, E. B. (1915). Linear Momentum, Kinetic Energy and Angular Momentum. The American Mathematical Monthly. Vol. XXII. Ginn and Co., Boston, in cooperation with University of Chicago, et al. p. 191, Theorem 8 – via Google books.
- ^ Synge and Schild, 텐서 미적분, 도버 출판물, 1978년판, 161쪽. ISBN 978-0-486-63612-2.
- ^ de Podesta, Michael (2002). Understanding the Properties of Matter (2nd, illustrated, revised ed.). CRC Press. p. 29. ISBN 978-0-415-25788-6.
- ^ R.P. Feynman; R.B. Leighton; M. Sands (1964). Feynman's Lectures on Physics (volume 2). Addison–Wesley. pp. 31–7. ISBN 978-0-201-02117-2.
- ^ 홀 2013 섹션 17.3
- ^ Veltman, Martinus J G (2018). Facts And Mysteries In Elementary Particle Physics (revised ed.). World Scientific. ISBN 978-981-323-707-0.
- ^ Thaller, Bernd (2005). Advanced Visual Quantum Mechanics (illustrated ed.). Springer Science & Business Media. p. 114. ISBN 978-0-387-27127-9.
- ^ Strange, Paul (1998). Relativistic Quantum Mechanics: With Applications in Condensed Matter and Atomic Physics (illustrated ed.). Cambridge University Press. p. 64. ISBN 978-0-521-56583-7.
- ^ Ballantine, K. E.; Donegan, J. F.; Eastham, P. R. (2016). "There are many ways to spin a photon: Half-quantization of a total optical angular momentum". Science Advances. 2 (4): e1501748. Bibcode:2016SciA....2E1748B. doi:10.1126/sciadv.1501748. PMC 5565928. PMID 28861467.
- ^ J. H. Van Vleck (1951). "The Coupling of Angular Momentum Vectors in Molecules". Rev. Mod. Phys. 23 (3): 213. Bibcode:1951RvMP...23..213V. doi:10.1103/RevModPhys.23.213.
- ^ Littlejohn, Robert (2011). "Lecture notes on rotations in quantum mechanics" (PDF). Physics 221B Spring 2011. Retrieved 13 Jan 2012.
- ^ Okulov, A Yu (2008). "Angular momentum of photons and phase conjugation". Journal of Physics B: Atomic, Molecular and Optical Physics. 41 (10): 101001. arXiv:0801.2675. Bibcode:2008JPhB...41j1001O. doi:10.1088/0953-4075/41/10/101001.
- ^ Okulov, A.Y. (2008). "Optical and Sound Helical structures in a Mandelstam – Brillouin mirror". JETP Letters (in Russian). 88 (8): 561–566. Bibcode:2008JETPL..88..487O. doi:10.1134/s0021364008200046. S2CID 120371573. Archived from the original on 2015-12-22. Retrieved 2015-10-31.
- ^ "Tropical Cyclone Structure". National Weather Service. Retrieved January 4, 2022.
- ^ Newton, Isaac (1803). "Axioms; or Laws of Motion, Law I". The Mathematical Principles of Natural Philosophy. Andrew Motte, translator. H. D. Symonds, London. p. 322 – via Google books.
- ^ Newton, Axioms; 또는 운동의 법칙, 결과 III
- ^ 역사를 통해 각운동량의 개념에 대한 훌륭하고 자세한 요약은 를 참조하십시오.
- ^ Bruce, Ian (2008). "Euler : Mechanica Vol. 1".
- ^ "Euler's Correspondence with Daniel Bernoulli, Bernoulli to Euler, 04 February, 1744" (PDF). The Euler Archive.
- ^ Rankine, W. J. M. (1872). A Manual of Applied Mechanics (6th ed.). Charles Griffin and Company, London. p. 506 – via Google books.
- ^ Hayward, Robert B. (1864). "On a Direct Method of estimating Velocities, Accelerations, and all similar Quantities with respect to Axes moveable in any manner in Space with Applications". Transactions of the Cambridge Philosophical Society. 10: 1. Bibcode:1864TCaPS..10....1H.
- ^ 예를 들어,
- ^ 예를 들어,
추가 정보
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2006). Quantum Mechanics (2 volume set ed.). John Wiley & Sons. ISBN 978-0-471-56952-7.
- Condon, E. U.; Shortley, G. H. (1935). "Especially Chapter 3". The Theory of Atomic Spectra. Cambridge University Press. ISBN 978-0-521-09209-8.
- Edmonds, A. R. (1957). Angular Momentum in Quantum Mechanics. Princeton University Press. ISBN 978-0-691-07912-7.
- 를 클릭합니다Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, vol. 267, Springer, ISBN 978-0-387-40122-5.
- Jackson, John David (1998). Classical Electrodynamics (3rd ed.). John Wiley & Sons. ISBN 978-0-471-30932-1.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 978-0-534-40842-8.
- Thompson, William J. (1994). Angular Momentum: An Illustrated Guide to Rotational Symmetries for Physical Systems. Wiley. ISBN 978-0-471-55264-2.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0809-4.
- Feynman R, Leighton R, and Sands M. (September 2013). "19–4 Rotational kinetic energy". The Feynman Lectures on Physics. The Feynman Lectures Website (online ed.).
{{cite book}}: CS1 maint: 작성자 파라미터 사용(링크)
외부 링크
- "잠수함, 로켓, 축구의 공통점은 무엇입니까?왜 프로레이트 구상체가 성공을 위한 형태인가」(Scientific American, 2010년 11월 8일)
- 각운동량 보존 – 온라인 교과서의 한 장
- 충돌 과정에서의 각운동량 – 3차원 사례의 파생
- 각운동량과 롤링모션– 더 많은 운동량 이론





 각운동량은
각운동량은  확장할 수 있다.
확장할 수 있다.









 공역운동량(표준운동량이라고도 함)으로 정의하는 것이다.
공역운동량(표준운동량이라고도 함)으로 정의하는 것이다. 원 안에서 움직이도록 구속된
원 안에서 움직이도록 구속된















 됩니다.
됩니다.

 위와 같이 동작의 수직 성분입니다.
위와 같이 동작의 수직 성분입니다.
 , 여기서 모든 움직임은
, 여기서 모든 움직임은 







 양 r
양 r 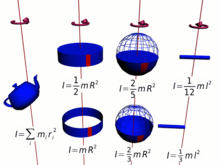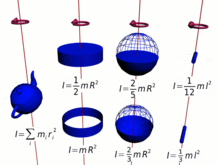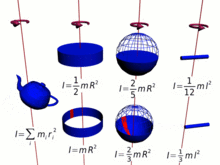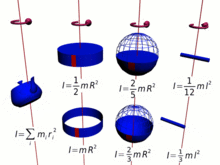










 환원됩니다.
환원됩니다.

 (는) 병렬 벡터입니다. 이
(는) 병렬 벡터입니다. 이  ) 병렬 벡터입니다.따라서 중심 주위의 물체의 각운동량은 일정합니다.행성이나
) 병렬 벡터입니다.따라서 중심 주위의 물체의 각운동량은 일정합니다.행성이나 









 z축 주위의 각도입니다.
z축 주위의 각도입니다. 
















 종종 궤도 역학 계산에서 중요하지
종종 궤도 역학 계산에서 중요하지 




 원점을 포함한
원점을 포함한 원점을 포함한 질량 중심 위치 벡터입니다.
원점을 포함한 질량 중심 위치 벡터입니다. 원점을 포함한 질량 중심의 속도이다.
원점을 포함한 질량 중심의 속도이다. 질량 중심을 갖는 입자
질량 중심을 갖는 입자





![{\displaystyle {\begin{aligned}\mathbf {L} &=\sum _{i}\left[\left(\mathbf {R} +\mathbf {r} _{i}\right)\times m_{i}\mathbf {V} _{i}\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} _{i}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77077ef30b49ac992b78c6a4c6446709bb1720a9)
![{\displaystyle {\begin{aligned}\mathbf {L} &=\sum _{i}\left[\mathbf {R} \times m_{i}\left(\mathbf {V} +\mathbf {v} _{i}\right)+\mathbf {r} _{i}\times m_{i}(\mathbf {V} +\mathbf {v} _{i})\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} +\mathbf {R} \times m_{i}\mathbf {v} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} +\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\right]\\&=\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} +\sum _{i}\mathbf {R} \times m_{i}\mathbf {v} _{i}+\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4784bd78e4066783f47bd72472bfa49a0887b0bf)





![{\displaystyle {\begin{aligned}\mathbf {L} &=M(\mathbf {R} \times \mathbf {V} )+\sum _{i}\left[m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&={\frac {R^{2}}{R^{2}}}M\left(\mathbf {R} \times \mathbf {V} \right)+\sum _{i}\left[{\frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&=R^{2}M\left({\frac {\mathbf {R} \times \mathbf {V} }{R^{2}}}\right)+\sum _{i}\left[r_{i}^{2}m_{i}\left({\frac {\mathbf {r} _{i}\times \mathbf {v} _{i}}{r_{i}^{2}}}\right)\right],\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5324c7fa7e5e94893f678fab046c2538416bc51)




















 x, y 또는 z와
x, y 또는 z와 




![{\displaystyle \left[\hbar ^{2}n(n+1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd720bdca13e8588818fb477347fb90c9789bb4a)














 고전
고전