스태틱스

시리즈의 일부
고전 역학
$({displaystyle {textbf {F}}=squalfrac {d}{dt}})(m*textbf {v}})$ 운동 제2법칙
역사 타임라인 교재
나뭇가지 응용의 천상의 연속체 다이내믹스 운동학 동력학 스태틱스 통계
기초 액셀러레이션 각운동량 커플 달랑베르의 원리 에너지 동적인 잠재적인 힘. 기준범위 관성 기준 프레임 충동 관성/관성 모멘트 덩어리 기계력 기계 작업 순간. 모멘텀 공간 스피드 시간을 토크 속도 가상 작업
제제 뉴턴의 운동 법칙 해석역학 라그랑주 역학 해밀턴 역학 루시아 역학 해밀턴-야코비 방정식 아펠 운동 방정식 쿱만-본 노이만 역학
주요 토픽 감쇠비 변위 운동 방정식 오일러의 운동 법칙 가공의 힘 마찰 고조파 발진기 관성/비관성 기준 프레임 평면 입자 운동 역학 움직임(선형) 뉴턴의 만유인력의 법칙 뉴턴의 운동 법칙 상대 속도 강체 역학 오일러 방정식 단순 고조파 운동 진동
회전 원운동 회전 기준 프레임 구심력 원심력 반응성 코리올리 힘 진자 접선 속도 회전 속도 각도 가속도/변위/주파수/속도
과학자 케플러 갈릴레오 호이겐스 뉴턴 경이다. 호록스 핼리 모페르튀이 다니엘 베르누이 요한 베르누이 오일러 달랑베르 클라이어트 라그랑주 라플라스 해밀턴 포아송 코시 러스 리우빌 어필 깁스 쿠프만 폰 노이만
물리 포털 카테고리
v t

정역학(Statics)은 가속(a=0)을 경험하지 않고 오히려 환경과 정적 평형 상태에 있는 물리적 시스템에 작용하는 (힘과 토크, 즉 "변화")의 해석과 관련된 고전 역학의 한 분야이다.시스템에 대한 뉴턴의 제2법칙의 적용은 다음을 제공합니다.

$(\displaystyle\textbf {F}}=m{\textbf {a}),}$

여기서 굵은 글꼴은 크기와 방향을 가진 벡터를 나타냅니다.$(디스플레이$ 스타일)는 시스템에 작용하는 힘의 합계, $(디스플레이 스타일$ m$)$은 시스템의$$ 질량,$$\($디스플레이$ 스타일$)$은 시스템의 가속도입니다.힘의 합계는 가속도의 방향과 크기를 제공하며 질량에 반비례합니다.$\display$\style ${textbf$ {$a}}$ =$$ 0의 $정적{\displaystyle }$ 평형 가정은 다음과 같다.

$(\displaystyle\textbf {F}}=0, .}$

알 수 없는 힘의 합계를 통해 알 수 없는 힘을 찾을 수 있습니다.정적 평형 상태에서는 시스템의 가속도가 0이고 시스템이 정지해 있거나 질량의 중심이 일정한 속도로 움직입니다.마찬가지로 시스템에 작용하는 모멘트의 합계에 가속도가 0이라는 가정을 적용하면 다음과 같이 됩니다.

${\displaystyle {M}}=I\alpha=0,}$

여기서 M$(\$은 시스템에 작용하는 모든 모멘트의 $합계$이고$,$ I(\$displaystyle$ I$)$는 질량의 관성 모멘트와$$α(\$displaystyle \alpha}$ =$$ 0)는 시스템의 각 가속도를 나타냅니다. 0으로 가정할 경우 다음과 같이 됩니다.

$(\displaystyle\textbf {M}}=0,}$

알 수 없는 모멘트의 합계를 통해 알 수 없는 모멘트를 찾을 수 있습니다.이 두 방정식을 함께 적용하여 시스템에 작용하는 부하(힘 및 모멘트)를 최대 2개까지 풀 수 있습니다.

뉴턴의 제1법칙에 따르면, 이는 시스템의 모든 부분에 대한 순 힘과 순 토크가 0이라는 것을 의미합니다.0에 해당하는 순 힘은 평형의 첫 번째 조건으로 알려져 있으며, 0에 해당하는 순 토크는 평형의 두 번째 조건으로 알려져 있습니다.'정적 불확정'을 참조하십시오.

역사

아르키메데스 (기원전 287년경–기원전 212년경)는 ^[1][2]정역학의 선구적인 연구를 했다.통계학 분야에서의 이후의 발전은 Thebit의 ^[3]작품에서 찾아볼 수 있다.

벡터

스칼라는 질량이나 온도와 같은 크기만을 가진 양입니다.벡터는 크기와 방향을 가지고 있다.벡터 식별에는 다음과 같은 몇 가지 표기가 있습니다.

• 대담한 얼굴의 캐릭터 V
• 밑줄 친 문자 V
• 화살표가 $표시$된 캐릭터 V $→$ {\$displaystyle${\$overright$arrow {$V$

벡터는 평행사변형 법칙 또는 삼각법칙을 사용하여 추가됩니다.벡터는 직교 기저에 성분을 포함합니다.단위 벡터 i, j, k는 각각 x축, y축, z축에 따른 규칙이다.

힘.

힘은 한 몸이 다른 신체에 가하는 작용이다.힘은 밀거나 당기는 것이며, 그 작용의 방향으로 물체를 움직이는 경향이 있다.힘의 작용은 그 크기, 작용 방향 및 적용 지점에 의해 특징지어집니다.따라서, 힘은 벡터량이다. 왜냐하면 그 효과는 ^[4]작용의 크기뿐만 아니라 방향에 따라서도 달라지기 때문이다.

힘은 접촉력 또는 신체력으로 분류된다.접촉력은 직접 물리적 접촉에 의해 생성되며, 예를 들어 지지면에 의해 물체에 가해지는 힘이다.본체의 힘은 중력장, 전기장 또는 자기장 등의 힘장 내에서의 본체의 위치에 의해 발생하며 다른 물체와의 접촉과는 무관하다.물체의 힘의 예는 지구 중력장에 ^[5]있는 물체의 무게이다.

힘의 모멘트

힘이 가해지는 방향으로 몸을 움직이는 경향에 가세해, 축을 중심으로 몸을 회전시키는 경향도 있다.축은 힘의 작용선과 교차하지 않거나 평행하지 않은 선일 수 있다.이러한 회전 경향을 힘의 모멘트(M)라고 합니다.모멘트는 토크라고도 합니다.

한 점에 대한 순간

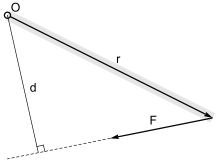
점 O에서 힘의 모멘트의 크기는 O에서 F의 작용선까지의 수직 거리에 힘의 크기를 곱한 것과 같다: M = F · d, 여기서

F = 가해지는 힘

d = 축에서 힘의 작용선까지의 수직 거리.이 수직 거리를 모멘트 암이라고 합니다.

순간의 방향은 오른쪽 규칙으로 지정됩니다.여기서 반시계방향(CCW)은 페이지 밖으로, 시계방향(CW)은 페이지 안으로 들어갑니다.모멘트 방향은 시계 반대 방향의 플러스 기호(+)와 시계 반대 방향의 마이너스 기호(-)와 같은 명시된 기호 규칙을 사용하여 설명할 수 있습니다.모멘트는 벡터로 합산할 수 있습니다.

벡터 형식에서 모멘트는 반지름 벡터 r(점 O에서 작용선까지의 벡터)와 힘 벡터 ^[6]F 사이의 교차곱으로 정의할 수 있습니다.

${\displaystyle {M}}_{O}=\textbf {r}\times {\textbf {F}}$

${\displaystyle r=\leftflash{array}{cc}x_{00}&...&x_{0j}\x_{01}&...&x_{1j}\\......\\x_{i0}&...x_{ij}\\end {array}\right}$

${\displaystyle F=\left({\begin{array}{cc}f_{00}&...&f_{0j}\\f_{01}&...&f_{1j}\...&...\\f_{i0}&...&f_{ij}\\end {array}\right}$

바리뇽의 정리

바리뇽의 정리는 어떤 점에 대한 힘의 모멘트는 같은 점에 대한 힘의 성분들의 모멘트의 합과 같다고 말한다.

평형 방정식

입자의 정적 균형은 정역학에서 중요한 개념이다.입자에 작용하는 모든 힘의 결과가 0일 때만 입자는 평형 상태에 있다.직사각형 좌표계에서 평형 방정식은 3개의 스칼라 방정식으로 나타낼 수 있으며, 여기서 세 방향의 힘의 합계는 0이다.이 개념의 공학적 적용은 부하가 걸린 최대 3개의 케이블의 장력을 결정하는 것입니다. 예를 들어 물체를 들어올리는 호이스트의 각 케이블이나 ^[7]열기구 지면에 고정하는 가이 와이어의 각 케이블에 가해지는 힘입니다.

관성 모멘트

고전 역학에서, 질량 모멘트, 회전 관성 모멘트, 질량의 극성 관성 모멘트 또는 각질량(SI 단위 kg·m²)은 회전 변화에 대한 물체의 저항의 척도입니다.회전하는 물체의 회전 관성입니다.관성 모멘트는 회전 역학에서 질량이 선형 역학에서와 거의 같은 역할을 하며, 각 운동량과 각 속도, 토크와 각 가속도 및 몇 가지 다른 양 사이의 관계를 설명합니다.기호 I와 J는 보통 관성 모멘트 또는 극성 관성 모멘트를 나타낼 때 사용됩니다.

관성 모멘트의 간단한 스칼라 처리로 많은 상황에서 충분하지만, 보다 발전된 텐서 처리로 팽이 돌기나 자이로스코프 운동과 같은 복잡한 시스템을 분석할 수 있다.

이 개념은 레온하르트 오일러에 의해 그의 1765년 저서 Theoryia motus corpus solidorum seu rigidorum에서 소개되었습니다; 그는 관성의 순간과 관성의 주요 축과 같은 많은 관련 개념에 대해 논의했습니다.

솔리드

정적학은 구조 분석, 예를 들어 건축 및 구조 공학에서 사용됩니다.재료의 강도는 정적 평형의 적용에 크게 의존하는 역학의 관련 분야이다.핵심 개념은 정지 상태의 물체의 무게 중심입니다. 물체의 모든 질량이 존재하는 가상 지점을 나타냅니다.물체가 놓여 있는 기초에 상대적인 점의 위치에 따라 외력에 대한 반응의 안정성이 결정된다.무게 중심이 기초 외부에 존재할 경우, 차체가 불안정하게 됩니다. 토크가 작용하기 때문입니다. 작은 교란으로 인해 차체가 떨어지거나 넘어집니다.기초 내에 무게 중심이 존재하면 차체에 작용하는 순 토크가 없기 때문에 차체가 안정적입니다.무게중심이 기초와 일치하면 몸이 전이된다고 한다.

유체

유체 정적으로도 알려진 유체 정역학(hydrodstatics)은 정지 상태의 유체에 대한 연구이다(즉, 정적 평형 상태).정지 상태의 유체의 특성은 유체의 입자에 가해지는 힘이 유체 내부의 동일한 깊이(또는 고도)에서 모든 지점에서 동일하다는 것입니다.순 힘이 0보다 크면 유체가 결과 힘의 방향으로 이동합니다.이 개념은 1647년 프랑스의 수학자이자 철학자 블레즈 파스칼에 의해 약간 확장된 형태로 처음 공식화되었고 파스칼의 법칙으로 알려지게 되었다.그것은 유압학에서 많은 중요한 응용 분야를 가지고 있다.아르키메데스, Abu Rayhann al-Binirun^[8] galileo, Al-Khazini, Galileo Galilei 또한 유체정역학 발전에 있어 주요한 인물이었다.

「 」를 참조해 주세요.

• 크레모나도
• 다이내믹스
• 기계적 평형
• 고체 역학

메모들

레퍼런스

• Beer, F.P. & Johnston Jr, E.R. (1992). Statics and Mechanics of Materials. McGraw-Hill, Inc.
• Beer, F.P.; Johnston Jr, E.R.; Eisenberg (2009). Vector Mechanics for Engineers: Statics, 9th Ed. McGraw Hill. ISBN 978-0-07-352923-3.

외부 링크

• 통계학 개념 지식 온라인 테스트(교사 대상)
• 힌트와 피드백을 포함한 약 300개의 인터랙티브 연습이 있는 무료 엔지니어링 통계 코스웨어: Carnegie Mellon Open Learning Initiative
• 로보틱스 통계

• [1] 2013-06-03년 Wayback Machine에 보관
• 엔지니어링 통계학– 네브래스카 대학교 링컨 과정