외부 대수
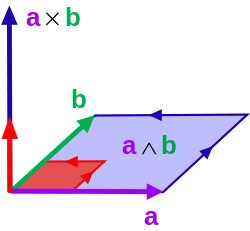
Exterior algebra수학에서, 헤르만 그라스만의 [3]이름을 딴 외부 대수 또는 그라스만 대수는 외부 곱이나 쐐기 곱을 곱으로 사용하는 대수이다.수학에서 벡터의 외부곱 또는 쐐기곱은 기하학에서 영역, 부피 및 그 고차원 유추들을 연구하기 위해 사용되는 대수적 구조이다.두 벡터와의 외부 곱( \ u \ v은 바이벡터(bivector)라고 불리며 벡터 본래의 공간과는 다른 벡터 공간인 외부 정사각형(external square)에 존재한다.The magnitude[4] of can be interpreted as the area of the parallelogram with sides and , which in three dimensions can also be computed using the cross product of the two vectors.일반적으로 방향과 면적이 동일한 모든 평행 평면 표면에는 방향 면적의 측정값과 동일한 쌍방향 벡터가 있습니다.교차곱과 마찬가지로 외부곱은 반교합적이어서 모든 u {\u} v {\ v-(에 대하여 the v - ( display u )이지만 교차곱과 달리 외부곱은 연관성이 있습니다.
이렇게 볼 때 두 벡터의 외부 곱을 2-블레이드라고 합니다.보다 일반적으로, 임의의 수의 k개의 벡터의 외부 곱을 정의할 수 있으며, 때로는 k-블레이드라고도 합니다.그것은 k번째 외부 전력으로 알려진 공간에 산다.3차원 벡터의 스칼라 삼중곱의 크기가 해당 벡터에 의해 생성된 평행입방체의 부피를 제공하는 것과 마찬가지로, 결과 k-블레이드의 크기는 모서리가 주어진 벡터인 k차원 평행입방체의 방향 하이퍼볼륨이다.
외부 대수는 기하학적 질문에 답하기 위한 대수적 설정을 제공한다.예를 들어 블레이드는 구체적인 기하학적 해석을 가지며, 외부 대수의 오브젝트는 일련의 명확한 규칙에 따라 조작할 수 있다.외부 대수는 k-블레이드일 뿐만 아니라 k-블레이드의 합인 객체를 포함한다. 이러한 합을 [5]k-벡터라고 한다.k-블레이드는 벡터의 단순한 산물이기 때문에 대수의 단순한 요소라고 불립니다.임의의 k-벡터의 순위는 합계가 되는 최소 수의 단순 요소로 정의됩니다.외부 곱은 완전 외부 대수까지 확장되므로 대수의 두 요소를 곱하는 것이 의미가 있습니다.이 곱을 갖춘 외부 대수는 연관 대수로, αβ \ β \ \ \ \ the \ \ \ the \ the ( \ display style \ alpha ( \ \ displa \ displesign \ discape ) \ \ the the \ the the the the the the the the the the the the the the the the k 벡터의 곱의 합계.다른 차수의 원소가 곱될 때, 그 차수는 다항식의 곱셈처럼 더해진다.이것은 외부 대수가 등급이 매겨진 대수라는 것을 의미한다.
외부 대수의 정의는 기하학적 벡터뿐만 아니라 벡터장이나 함수와 같은 다른 벡터 유사 객체의 공간에도 의미가 있습니다.완전일반성에서는 외부대수는 교환환 상의 모듈 및 추상대수의 다른 관심 구조들에 대해 정의될 수 있다.이것은 외부 대수가 가장 중요한 응용 프로그램 중 하나를 찾는 보다 일반적인 구조 중 하나이며, 여기서 그것은 미분 기하학을 사용하는 영역에서 기초적인 미분 형식의 대수로서 나타난다.외부대수는 또한 대수학 자체에서 편리한 도구로 만드는 많은 대수적 특성들을 가지고 있다.벡터 공간에 대한 외부 대수의 연관성은 벡터 공간의 함수의 한 종류로, 벡터 공간의 선형 변환과 특정한 방식으로 호환된다는 것을 의미합니다.외형대수는 이중공간에도 적자가 있음을 의미하는 바이알대수의 한 예이며, 이 이중적자는 외형대수의 한 예이다.이 이중 대수는 정확히 교대 다선형 형태의 대수이며, 외부 대수와 그 이중 대수의 쌍은 내부 곱에 의해 주어진다.
동기 부여 사례
평면 내 영역
데카르트 ^{는 단위 벡터 쌍으로 구성된 기저를 갖춘 실제 벡터 공간이다.
라고 가정해 보자
는R2(\에 기재된 주어진 벡터 쌍입니다.v와 w를 두 변으로 하는 독특한 평행사변형이 있다.이 평행사변형의 면적은 다음과 같은 표준 결정식 공식에 의해 주어진다.
이제 v 및 w의 외부 제품을 살펴보겠습니다.
여기서 첫 번째 단계는 외부 곱에 대한 분배 법칙을 사용하고 마지막 단계는 외부 곱이 교대로 존재한다는 사실을 사용합니다. 2 1 - ( 1 2) { style \ \ {} =-( { \ {e} { {f} {f} {f} { {f}oduct는 또한 { \ } { \ { \ mathbf { e } _ {2} \ } _ { )。이 마지막 식에서 계수는 행렬의 결정 요인입니다 [v w].이것이 양수이거나 음수일 수 있다는 사실은 v와 w가 정의되는 평행사변형의 꼭지점으로서 시계 반대 또는 시계 반대 방향으로 향할 수 있다는 직관적인 의미를 갖는다.이러한 영역을 평행사변형의 부호 영역이라고 부릅니다. 부호 영역의 절대값은 일반 영역이며, 부호는 그 방향을 결정합니다.
이 계수가 사인 영역이라는 사실은 우연이 아니다.사실, 이 영역을 대수적 구문으로 공리화하려고 하면 외부 곱이 서명된 영역과 관련되어야 한다는 것을 비교적 쉽게 알 수 있다.상세하게, A(v, w)가 벡터 v와 w 쌍이 인접한 두 변을 형성하는 평행사변형의 부호 영역을 나타낸다면, A는 다음 특성을 충족해야 한다.
- A(rv, sw) = rsA(v, w)는 어느 한 변의 면적을 동일한 양만큼 재스케일링하기 때문에(한 변의 방향을 반대로 하면 평행사변형의 방향이 반전된다).
- v에 의해 결정되는 퇴화 평행사변형(즉, 선분)의 면적은 0이므로 A(v, v) = 0이다.
- a(w, v) = -A(v, w), v와 w의 역할을 교환하면 평행사변형의 방향이 반전되기 때문이다.
- a(v + rw, w) = 임의의 실수 r에 대해 A(v, w)이다. 왜냐하면 w의 배수를 v에 더하면 평행사변형의 밑변이나 높이에 영향을 주지 않고 결과적으로 면적을 보존하기 때문이다.
- 단위 정사각형의 면적이 1이므로 A1(e2, e) = 1이다.
마지막 특성을 제외하고, 두 벡터의 외부 곱은 면적과 동일한 특성을 만족합니다.어떤 의미에서 외부제품은 평행사변형의 면적을 평행평면(여기서는 변1 e, e를2 가진 면) 중 선택된 평행사변형의 면적에 비교함으로써 최종성을 일반화한다.즉, 외부 제품은 베이스에 의존하지 않는 영역의 [6]공식을 제공한다.
크로스 및 트리플 제품
2차원 스칼라 곱을 갖는 3차원 배향 벡터 공간에서의 벡터의 경우, 외부 대수는 교차곱 및 삼중곱과 밀접하게 관련된다.표준 기준(e1, e2, e3)을 사용하여 벡터 쌍의 외부 곱
그리고.
이
여기서 (e12 , e2, e3 , e3, e1 is e)는 공간2 R 3 style \ ^{{R}}\right의 기초입니다.위의 계수는 주어진 방향을 가진 3차원 벡터의 교차곱에 대한 일반적인 정의와 동일하며, 유일한 차이점은 외부곱이 일반 벡터가 아니라 2-벡터이며, 외부곱은 방향 선택에 의존하지 않는다는 것이다.
제3의 벡터를 도입하다
세 벡터의 외부 곱은
여기서1 e e2 e e3 e는 1차원 공간3 ( 3^{^{의 기본 벡터입니다.스칼라 계수는 세 벡터의 세 곱이다.
3차원 유클리드 벡터 공간에서의 교차곱과 삼중곱은 각각 기하학적 해석과 대수적 해석을 모두 받아들인다.교차곱 u × v는 u와 v 모두에 수직이고 크기가 두 벡터에 의해 결정되는 평행 사변형의 면적과 동일한 벡터로 해석될 수 있다.또한 u 및 v 열이 있는 행렬의 부행렬로 구성된 벡터로도 해석할 수 있습니다.u, v, w의 3중 곱은 기하학적 지향 볼륨을 나타내는 부호 있는 스칼라입니다.대수적으로, 이것은 열 u, v, w가 있는 행렬의 행렬식이다.3차원의 외부 제품도 마찬가지로 1개 또는 2개 이상의 벡터에 걸쳐 있는 방향선, 면적, 볼륨 등과 식별할 수 있습니다.외부 곱은 스칼라 곱이 없는 경우에도 이러한 기하학적 개념을 모든 벡터 공간 및 임의의 수의 차원으로 일반화합니다.
형식적 정의와 대수적 특성
필드 K 위의 벡터 공간 V의 외부 대수δ( {{는 x δV 형식의 모든 요소에 의해 생성된 양면 이상 I에 의해 텐서 대수 T(V)의 몫 대수로서 정의된다(즉, V의 곱으로 표현될 수 있는 모든 텐서).아이디얼 I에는 x + y x (+ )- x - y \ x + \ x = (+ y )\ ( x + y )\otimes= ( x + y )\ ( x + y display x + y\ times x - y\ times x - y\ times x - y \ times x y \ times x y \ times x of y \ times x these y \times x 이러한 이상은 제로 벡터 공간을 제외하고 다릅니다.
그렇게,
는 연관대수입니다.곱셈을 외적이라 하고 denoted로 표기한다.즉, T(V)의 텐서 곱 θ에 의해θdisplaystyle 의 곱이 유도됨을 의미한다.
T0 = K, T1 = V 및( ( ) T ()i I { ( \ \ ( 0 } ( ) \ T^ { ( ) \ right )\I= \ { 0 \ 0\ 0 \ } i 、 V t t as as 、 V t t as 、 、 。이러한 주입은 일반적으로 포함물로 간주되며, 자연 매립물, 자연 주입물 또는 자연 포함물이라고 합니다.canical이라는 단어는 또한 자연 대신 일반적으로 사용된다.
대체 제품
외부 제품은위 구조에 의해 모든 \ x \ V \ x \ display x 0인 V \ styleV 를 번갈아 시공합니다.따라서 제품은 X V x V로 가정하기 위해 V V 에서도 반작용적입니다.
이런 이유로
보다 일반적으로 θ가 정수 [1, ..., k]의 순열이고 x1, x2, ..., x가k V의 요소라면 다음과 같이 된다.
여기서 sgn(signature)은 치환의 시그니처입니다.[8]
특히, x = x일j 때i, 일부 i µ j에 대해, 다음과 같은 교대 특성 일반화도 성립한다.
외부 제품의 분포 특성과 함께, 한 가지 더 일반화된 것은 { 1, 2,,, { },가 선형 종속 벡터 집합일 경우에만 해당한다는 것입니다.
외부 전원
k( V ) \ \\ { }\ ( \ 로 표시된 V의 k번째 외부 거듭제곱은 형식의 요소에 의해 확장된 () \ ( )의 벡터 부분 공간입니다.
α ( ) \ \ \ \ ^ { }\ ( \ )이면 α는 k 벡터라고 한다.만약, 게다가 α V의 k요소 외부 제품으로 표현될 수 있다면 α 분해할 수 있는 것으로 알려져 있다.비록 분해할 수 있는 k-vectors⋀ k스팬({\displaystyle \bigwedge \nolimits ^{km그리고 4.9초 만}(V\right)}, ⋀ k의 모든 요소({\displaystyle \bigwedge \nolimits ^{km그리고 4.9초 만}(V\right)}분해할 수 있는 있다.예를 들어 R4{\displaystyle \mathbb{R}^{4},}에 다음과 같은 2-vector:분해할 수 있는 것이 아니다.
(α α α 0 0이므로 이것은 심플렉틱 형태이다.)[9]
기초 및 치수
V의 치수가 n이고 {e1, …, en}가 V의 기준인 경우 집합은
는" ( {^{의 기본입니다.그 이유는 다음과 같습니다.양식의 외부 제품을 지정하면
모든 벡터j v는 기저 벡터i e의 선형 조합으로 쓸 수 있다. 외부 곱의 이중성을 사용하여 이러한 기저 벡터의 외부 곱의 선형 조합으로 확장할 수 있다.동일한 기저 벡터가 여러 번 나타나는 외부 곱은 0이며, 기저 벡터가 올바른 순서로 나타나지 않는 외부 곱은 정렬할 수 있으며, 두 기저 벡터가 위치를 바꿀 때마다 부호를 변경할 수 있다.일반적으로 기저 k-벡터의 결과 계수는 벡터j v를 기저i e로 기술하는 행렬의 부계수로 계산할 수 있다.
기본 요소를 카운트함으로써k () \ \ ^ {의 치수는 이항계수와 같습니다.
여기서 n은 벡터의 차원이고 k는 곱의 벡터 수입니다.이항계수는 예외적인 경우에도 정확한 결과를 산출한다. 특히 k > n의 경우k () \\ ^{ = { 0 }이다.
외부 대수의 모든 요소는 k 벡터의 합으로 쓸 수 있다.따라서 벡터 공간으로서 외부 대수는 직합이다.
(여기서 규칙 ( V) \ \ \^ { } \ ( \ )=K V의 기초가 되는 필드 및 (V) =displaystyle \right)=V이므로 그 차원은 이항 계수의 합인n 2와 같다
k-벡터의 등급
α ∈( ) \ \^{인 경우 분해 가능한 k 벡터의 선형 조합으로 α를 표현할 수 있습니다.
예를(i) 들어, 각 α는 분해할 수 있다.
k-벡터 α의 순위는 그러한 α의 팽창에서 분해 가능한 k-벡터의 최소 개수이다.이것은 텐서 등급의 개념과 유사하다.
순위는 2-벡터의 연구에서 특히 중요하다(Sternberg 1964, §II.6). (Bryant et al. 1991).2-벡터 α의 순위는 α 계수 행렬의 반값으로 식별할 수 있다.따라서i 만약 e가 V의 기초라면, α는 다음과 같이 독특하게 표현될 수 있다.
여기서ij a = -aji(계수의 행렬은 스큐-스큐 행렬)입니다.따라서ij 행렬 a의 순위는 짝수이며, 형식 α의 2배이다.
특성 0에서 2-벡터 α는 다음과 같은 경우에만 등급 p를 갖는다.
- ∧ p { { } { \ \ \ \ \ 0 ∧ ∧ ∧ ∧⏟ α ⏟ ⏟ ⏟ αα α α α α α α α α α α α α α α α α α α α α α α α α α α α α α α α
단계적 구조
p-벡터가 있는 k-벡터의 외부 곱은 (k + p)-벡터이며, 다시 한 번 쌍선형성을 호출합니다.그 결과, 전조의 직접합계 분해는
외부 대수에는 등급이 매겨진 대수의 추가 구조를 제공한다.
게다가 만약 K가 베이스 필드라면, 우리는
- 0 (V )= }^{\! = K} 및 (V = . \ \ }^{\!=V .
외부 곱은 반상환 등급으로 매겨집니다. 즉, α k() \ \ \ \ ^ { } \ ( \ ) β () \ \ beta \ \ \ ^ { ^ { } \ nolimits ( V \ nright ( V \ nright}일 경우 과 같이 됩니다.
Bourbaki(1989)는 외부 대수에 대한 등급부 구조를 연구하는 것 외에 등급부 모듈(이미 자체의 계조를 갖는 모듈)의 외부 대수에 대한 것과 같은 외부 대수에 대한 추가 등급부 구조를 연구한다.
보편적 재산
V를 필드 K 위의 벡터 공간이라고 하자.비공식적으로 ( ) \ \ left ( \ 의 곱셈은 기호를 조작하여 분배법칙인 관계법칙을 부과하고 v v V ∈ V ∈ V { }을 사용하여 수행됩니다. 정식으로 v \ \ v ) \ wed \ wed \ ( V )이러한 규칙이 곱셈에 적용되는 대수. 즉, V에 번갈아 곱셈을 하는 V를 포함하는 단수 대응 는θ의 동형 이미지를 포함해야 한다. 즉, 외부 대수는 다음과 같은 보편적 [10]속성을 갖는다.
임의의 단수 연관 K-대수 A와 임의의 K-선형 지도 j : V → A가 V의 모든 v에 대해 j(v)j(v) = 0이면, 정확히 하나의 단수 대수 동형 f :θ ( \ → A가 존재한다. (위 참조).
V를 포함하고 곱셈이 V에서 교대로 이루어지는 가장 일반적인 대수를 구성하기 위해, V를 포함하는 가장 일반적인 연상 대수인 텐서 대수 T(V)에서 시작하여 적절한 몫을 취함으로써 교대 특성을 적용하는 것이 자연스럽다.따라서 V의 v v v 형식의 모든 요소에 의해 생성된 T(V)의 양면 아이디얼 I를 취하여 (V ) \ \ \right )를 몫으로 정의한다.
(및use( V)의 곱셈 기호로서 「」를 사용합니다.\ \ ( \ 。그러면 () \ \ ( \ )는 V를 포함하고 있으며 위의 보편적 특성을 충족한다는 것을 쉽게 알 수 있습니다.
결과, 벡터 공간 V에 그 외부 대수θ를 할당하는 연산은 벡터 공간 범주에서 대수 범주까지의 함수이다
먼저 ( )\ \ left ( \ )를 정의하고 다음으로 외부 파워( V){ \ { k }\ ( \right )를 특정 서브스페이스로 지정하는 것이 아니라 공간k ( ) \ style \ { nigweddge를 정의할 수 있습니다.st를 조합하여 대수 ( ) \ \ ( \ )를 만듭니다이 접근법은 종종 미분 기하학에서 사용되며 다음 절에서 설명합니다.
일반화
가환환 R과 R-모듈 M이 주어지면 위와 같이 외부대수 θdisplaystyle를 텐서대수 T(M)의 적절한 몫으로 정의할 수 있다.그것은 유사한 보편적 성질을 만족시킬 것이다.require( )\ \ ( \ )속성의 많은 부분에서도 M이 투영 모듈이어야 합니다.유한 차원성이 사용되는 경우, 속성은 M을 최종 생성 및 투영해야 합니다.가장 일반적인 상황에 대한 일반화는 부르바키(1989)에서 찾을 수 있다.
벡터 다발의 외부 대수는 기하학과 위상학에서 자주 고려된다.Serre-Swan 정리에 의해 유한 차원 벡터 다발의 외부 대수의 대수적 특성과 최종 생성된 투영 모듈의 외부 대수의 대수적 특성 사이에는 본질적인 차이가 없다.모듈 단에 대해 보다 일반적인 외부 대수를 정의할 수 있습니다.
교대 텐서 대수
K가 특성 [11]0의 장이라면, K 위의 벡터 공간 V의 외부 대수는 반대칭 텐서로 이루어진 T(V)의 벡터 부분 공간과 규범적으로 동정할 수 있다.외부 대수는 x x x 형태의 요소들에 의해 생성된 이상 I에 의한 T(V)의 몫이라는 것을 기억하라.
T(V)를 균질 텐서 r의 공간이라고 하자r.이것은 분해 가능한 텐서에 의해 확장됩니다.
분해 가능한 텐서의 반대칭성(또는 때때로 스큐-대칭성)은 다음과 같이 정의된다.
여기서 합계는 기호 {1, ..., r}의 대칭 순열 그룹에 대해 취해진다.이는 선형성과 동질성에 의해 전체 텐서 대수 T(V)에서 Alt로 표시되는 연산으로 확장된다.이미지 Alt(T(V))는 A(V)로 표시된 교대 텐서 대수입니다.이것은 T(V)의 벡터 부분 공간이며, T(V)의 그것으로부터 등급화된 벡터 공간의 구조를 계승한다. { } { {\ by by 。
이 곱은 텐서곱과 다르지만, Alt의 커널은 정확히 이상 I이며 (K가 특성 0을 갖는다고 가정하면) 정준 동형성이 존재한다.
색인 표기법
V가 유한 차원 n을 가지며, V의1 기저 e, ..., e가n 주어졌다고 가정하자.그러면 모든 교대 텐서 t ar A(V) tr T(V)는 지수 표기법으로 다음과 같이 쓸 수 있다.
여기서i1⋅⋅⋅ir t는 인덱스에서 완전히 반대칭입니다.
r과 p 등급의 두 교대 텐서 t와 s의 외부 곱은 다음과 같다.
이 텐서의 성분은 텐서 곱 s t t의 성분의 스큐 부분으로, 지수에 대괄호로 표시된다.
내부 제품은 다음과 같이 색인 표기법으로도 설명할 수 있다.t 0 1 r - { t=을 랭크 r의 반대칭 텐서라고 .그런 다음, α∗ δ V의 경우, 다음과α 같이 주어지는 r - 1 등급의 교대 텐서이다.
여기서 n은 V의 치수입니다.
이중성
교대 연산자
2개의 벡터 공간 V와 X와 자연수 k가 주어졌을 때, V에서k X로의 교대 연산자는 다선형 지도이다.
v, ..., v가k V의 선형 의존 벡터일 때마다1,
지도
외부인 해당 k( 스타일 k -벡터(즉, 하는 k k -벡터)의 KK) 와도 교대로 관련지어집니다.실제로 이 맵은 V에 된 " 일반적인" 교대 연산자이며, 다른 교대 f f X f w{\ f=\ w의 고유한 선형 맵 :k () { \} \ X가 존재합니다. 이 유니버설 속성은 \k ( )
교대로 다선형 형태
위의 설명은 기준 필드인 X = K인 경우를 전문으로 합니다.이 경우, 교대 다선형 함수
는 교대 다선형 형태라고 불립니다.모든 교대 다선형 형태의 집합은 벡터 공간이다. 두 개의 그러한 지도 또는 스칼라가 있는 그러한 지도의 곱의 합이 다시 교대하기 때문이다.외승의 보편적 특성에 의해, V 위의 도수 k의 교대 공간은 이중 벡터 공간k ( \ \ left ( \ style \ ( \ bigwedge \ ^ { } \ left ( \ )\ right 와 자연 동형이다.^{*}}. 만약 V, 만약 V다차원 그러면 후자는 자연스럽게({\displaystyle \bigwedge \nolimits ^{km그리고 4.9초 만}(V^{*}\right)}k⋀. 특히, isomorphic[해명 필요한]유한 차원의., 교대의 지도로 Vk K까지 그 공간의 치수는 이항 계수(nk).{\d.isplaystyle{\tbinom{n
이러한 식별 하에, 외부 제품은 구체적인 형태를 취합니다. 즉, 두 개의 특정 제품에서 새로운 반대칭 맵을 생성합니다.예를 들어 suppose : Vk → K와 : : Vm → K가 2개의 안티캐스팅 맵이라고 가정합니다.다중선형 지도의 텐서 곱의 경우와 마찬가지로, 외부 곱의 변수 개수는 변수 개수의 합이다.다중 선형 형태를 가진 외부 동력 요소의 식별 선택에 따라 외부 생성물은 다음과 같이 정의된다.
또는 로서
여기서 기준 필드 K의 특성이 0인 경우 다중 선형 맵의 교대 Alt는 변수의 모든 순열에서 부호 조정 값의 평균으로 정의된다.
필드 K가 유한 특성을 갖는 경우 인수나 상수가 없는 두 번째 식과 동등한 버전이 잘 정의됩니다.
여기서k,m Sh sk+m S는 세트 {1, 2, ..., k + m}의 (k, m) 셔플의 서브셋입니다.이것은, ( (1) < ( (2) < < ( k) 및 ( ( k + 1) < ( ( k + 2 ) < < ( k + m ) < < < σ σ σ σ σ where where where where where where where where where where 。
인테리어 제품
V가 유한 차원이라고 가정합니다.V가∗ 벡터 공간 V에 대한 이중 공간을 나타내면, 각 α δ∗ V에 대해 대수δ () \를 정의할 수 있다.
이 유도체는 α 또는 때로는 삽입 연산자 또는 α에 의한 수축과 함께 내부 산물이라고 불립니다.
{w \ \ ^ {} 。w는 V와 K의 다중∗ 선형 매핑이므로 k폴드 데카르트 곱 V∗ × V∗ × ... × V의 값에∗ 의해 정의됩니다.만약1 u2, uk−1, ..., ..., ..., V가 V의 요소인∗ 경우, 1을 정의합니다.
또한 f가 순수 스칼라( whenever Vα { display style \ \ })에 속한다고 가정합니다.
자명한 특성 및 속성
내장 제품은 다음 특성을 충족합니다.
- 각 k와 각 α µ∗ V에 대해(일반적으로 - { { \ \^ { -V= \ { \ } )
- v가 V의 요소인 경우( { =\
), ivα = α(v)는 V의 원소와 V의 원소∗ 사이의 이중 쌍이다.
- 각 α δ∗ V에 대해 i는α 도수 -1의 단계적 유도체이다.
이 세 가지 특성은 내부 제품의 특성뿐만 아니라 일반적인 무한 차원 사례에서 제품을 정의하기에 충분합니다.
인테리어 제품의 추가 특성은 다음과 같습니다.
호지 이중성
V의 차원 n이 유한하다고 가정합니다.그러면 내부 산출물은 벡터 공간의 표준 동형성을 유도한다.
재귀적 정의에 의하면
기하학적 설정에서는 1차원 벡터 공간인 최상위 외부전력n () \ \\ ^ { } \ ( \ 의 0이 아닌 요소를 볼륨형(또는 방향형)이라고 부르기도 합니다.다만, 이 용어가 불명확한 경우가 있습니다.오리엔테이션이란 이름은 벡터 공간의 질서 있는 기초를 고정하는 것과 같기 때문에 선호되는 상위 요소의 선택이 외부 대수 전체의 방향을 결정한다는 사실에서 유래한다.바람직한 부피 형태 θ에 대해 동형성은 명시적으로 다음과 같이 주어진다.
부피 형태와 더불어 벡터 공간 V에 V를∗ V로 식별하는 내부 곱이 있다면, 그 결과 생기는 동형성을 호지 별 연산자라고 하며, 원소를 호지 쌍체에 매핑합니다.
\\ (V) \ \ \ → ( ) \ \\ left \ → a k ( \ displaystyle \ ^ { k ^ { k \ right ( V \ right )의 구성은 항상 맵의 스칼라입니다.대부분의 애플리케이션에서 볼륨 형태는 V의 직교 기준의 외부 제품이라는 점에서 내부 제품과 호환됩니다.이 경우,
여기서 id는 아이덴티티 매핑이며, 내부 제품에는 메트릭시그니처(p, q)가 있습니다(puses 및 q minuses).
내부 제품
V가 유한 차원 공간인 경우, V 위의 내적(또는 의사-유클리드 내적)은 V와∗ V의 동형성을 정의하며, 따라서 k ^{와 V}V)의 동형성을 정의한다. 이 두 공간 간의 쌍은 내부 제품의 형태를 취합니다.분해 가능한 k-벡터에서는
내부 산물의 매트릭스 결정 요인특별한 경우i v = w에서i 내부곱은 gramian 행렬의 행렬식(θv, vθij)에 의해 주어진 k-합성의 제곱 노름이다.그런 다음, 이것은 의 비퇴화 생성물로 빌리너리 조기( 복합적인 경우 sesquilinary 만약i e, i = 1, 2, ..., n이 V의 정규 기저, 그리고 그 형태의 벡터,
k ( )\ \ \ ^ { }\ left ( \ )의 직교 기저를 구성합니다.
내적에는 외적 곱셈과 내적 곱셈이 서로 인접해 있다.구체적으로는 vk- ( ) \ v \\^ { k - \( \right 의 wdisplay( ) \ w \ \ \ ^ { \ display .
여기서♭ x v∗ V는 음악적 동형사상이며, 다음과 같이 정의된 선형함수이다.
모든 y v V에 대해.이 성질은 외부 대수의 내적을 완전히 특징짓는다.
일반적으로 v - ( V) \ \ \ { k - } \ left ( \right )、 \ \ \ \ { } \ \ ) 、 s
서 x ( ) l ( ) \ \ style { \ } \ \ bigwedge \^ { } \ ( ^ { * } \ ) \ ( \ \ \은(는) 정의되어 있는2개의 l-param입니다.
() \ y \ \ \ ^ { } \ \ right ) } }
바이알게브라 구조
등급 대수δ(의 쌍대와의 교대 다선형 형태 에는 대응 관계가 있다.외부 대수(대칭 대수뿐 아니라)는 텐서 대수로부터 바이알 대문자 구조, 그리고 실제로 홉프 대수 구조를 계승한다.주제에 대한 자세한 설명은 텐서 대수에 대한 기사를 참조하십시오.
위에서 정의한 다중선형 형태의 외부 곱은 () \ \left ( \ )에 정의된 공동생산물과 이중으로 되어 있어 연골대수의 구조를 제공한다.공동연산은 선형함수 : () \ left ( \ ) → (V) \ style \ \ ( V \ ) ( ) \ style \ \ ( \ ( V \ right ) 。
v'V로 설정합니다.기호 1은 필드 K의 단위 요소를 나타냅니다. ( () \ \ ( V \right ) ( () \ \ left ( V \ ) v 。이 공동제작의 정의는 (선형) 동형사상에 의해 ( \로 풀스페이스δ(V)로 확대된다.이 동형사상의 올바른 형태는 순진하게 쓸 수 있는 것이 아니라 연골문헌에서 신중하게 정의된 것이어야 한다.이 경우, 사람들은
이를 상세하게 확장하면 분해 가능한 요소에 대해 다음과 같은 식을 얻을 수 있습니다.
여기서 두 번째 합계가 모든 (p+1, k-p)-shuffle에 이어집니다.상기 내용은 필드 요소 1을 추적하기 위해 알림 트릭을 사용하여 작성됩니다. 이 트릭은 1(\1을 쓰는 것입니다. 이 트릭은 셔플 위로 합계가 확대되는 동안 여러 위치로 섞입니다.shuffle은 공동 대수의 첫 번째 공리부터 직접 이어집니다.k \ _{ k } 의 상대적 순서는 riffle shuffle로 유지됩니다.riffle shuffle은 순서가 매겨진 시퀀스를 왼쪽과 오른쪽의 2개의 순서로 분할하기만 하면 됩니다.
공동제작물이 대수의 등급을 유지하는지 관찰하십시오.풀스페이스( V ) \ displaystyle \\(V right )로 확장하면 다음과 같이 됩니다.
이 절에서 사용하는 텐서 기호 θ는 주의해서 이해해야 한다. 즉, 교대곱의 정의에 사용되는 텐서 기호와 동일하지 않다.직감적으로 보면, 텐서 곱으로 생각하기 가장 쉬운데, 텐서 곱은 여전히 (이중)선형이지만, 이중대수의 정의, 즉 오브젝트display () \ \ ( V \ )display ( ). 순진한 쐐기 기호의 정의에 따라 따르는 등식(1 µ v) 1 (1 µ w) = 1 ) (v µ w) 및 (v † 1) 1 (1 µ w) = v , w를 고려함으로써 여운을 남길 수 있다.이 구별은 텐서 대수에 관한 기사에서 더 자세히 개발된다.여기서 교대곱 θ는 2차 대수의 곱셈에 명확하게 대응하고 기호 θ는 2차 대수의 정의에 자유롭게 사용할 수 있다는 점에서 문제가 훨씬 적다.실제로는 하나의 예외를 제외하고 θ의 교대로 합계를 쐐기 기호로 치환하는 치명적인 트랩을 회피하는 한 특별한 문제가 발생하지 않습니다.다른 공간에서 동작하는 것을 이해하고, ,과 다른 제품을 구성할 수 있습니다.아래에 예를 제시하겠습니다.이중 공간에 대한 교대곱은 공동생산 측면에서 제시될 수 있습니다.여기서 바이알 대수의 구성은 외부 대수에 대한 교대 부호를 정확하게 추적할 필요성을 제외하고 텐서 대수 기사의 구성과 거의 정확하게 유사하다.
공동 제작의 관점에서, 이중 공간의 외부 제품은 공동 제작의 등급이 매겨진 이중 제품일 뿐입니다.
여기서 오른쪽 텐서 곱은 다선형 선형 맵(양립할 수 없는 균질도 요소에 대해 0으로 계산됨: 보다 정확하게는 α β = β β β β β β δ δ δ δ where where where where where where where where where where 、 it it it it it it where where where where where where where where where where where where where presently presently presently presently presently presently
counit은 동형사상 θ :θ ( V ) \ \ (\right )→ K이며, 인수의 0-제곱 성분을 반환한다.공동생산과 국가는 외부 산물과 함께 외부 대수에서 바이알대수의 구조를 정의한다.
S( ) ( -) ( x + ) {\ S) =1)^{\에 의해 정의된 대척수를 사용하면 외부 대수는 더욱 홉 [15]대수가 된다.
기능성
V와 W가 벡터 공간의 쌍이고 f : V → W가 선형 맵이라고 가정합니다.그리고 나서, 보편적 특성에 의해, 등급화된 대수의 독특한 동형이 존재한다.
그렇게 해서
특히 ( )\ \ ( f \ 는 균질도를 유지합니다.분해 가능한 요소에 대한 () \ \ left ( \ )의 k 등급 구성요소는 다음과 같이 지정됩니다.
허락하다
V와 W의 기저를 기준으로 한 변환k( ) \ displaystyle \ \nolimitsright)의 성분은 k × k f의 부행렬이다.특히 V = W 및 V가 유한 차원 n일 경우,n () { \ \ ^ { } \ ( \ )는 1차원 벡터 공간n () \ \\ ^ { n ^ { } \ left \ right의 매핑이며, 따라서 그 자체가 주어집니다.
정확성
0 { 0 W 0이(가) 벡터 공간의 짧은 시퀀스인 ,
다음과 같이 등급화된 벡터 [16]공간의 정확한 시퀀스입니다.
직접 합계
특히, 직합의 외부 대수는 외부 대수의 텐서 곱과 동형이다.
이것은 단계적 동형사상입니다. 즉,
일반적으로 벡터 0 V {\ 0 U0의 짧은 정확한 시퀀스에 대해 자연스러운 여과가 있습니다.
서 P의 F p \ F는 1 …k + - p v 1 …- \ \ wedge { + 1 \ u _ { 1 } \ \ \ } \ 。v_{ V 입니다.대응하는 인용구는 자연 동형성을 인정한다.
- p + / F - ( ) (( W) \ F+ / } \ cong { \ bigwedge }^{ \\ \}^{ {} ( + 1 by by by by by by by by byby by by by by by by by by by by by by by by k by by by by by by by by by k by by by by by by by
특히 U가 1차원이라면
정확하고 W가 1차원이라면
정확합니다.[18]
적용들
선형 대수
선형대수에 대한 응용에서 외부곱은 행렬의 행렬식 및 부계수를 기술하기 위한 추상적 대수적 방법을 제공한다.예를 들어, 정사각형 행렬의 행렬식은 행렬의 각 변이 행렬의 열인 평행동위원소의 부피와 동일하다는 것은 잘 알려져 있다.이는 행렬식을 열 벡터의 외부 곱으로 정의할 수 있음을 나타냅니다.마찬가지로 행렬의 k × k 마이너는 한 번에 k를 선택한 열 벡터의 외부 곱을 통해 정의할 수 있습니다.이러한 아이디어는 행렬뿐만 아니라 선형 변환으로도 확장될 수 있습니다. 선형 변환의 결정 인자는 주어진 참조 평행 동위원소의 방향 볼륨을 확장하는 요인입니다.따라서 선형 변환의 결정 요인은 변환이 최상위 외부 전력에 미치는 영향을 기준으로 정의할 수 있습니다.작은 외부 세력에 대한 변환의 작용은 변환의 마이너리티에 대해 말할 수 있는 근거에 의존하지 않는 방법을 제공합니다.
기술 상세:정의들
V[19] V를 필드 K 위의 n차원 벡터 공간으로 .기본값은 { {{1입니다.
- End V \ \ \ { ( , V \ \ ^ { } \{ } ( \ ^ { } )에 단순하게 정의합니다정의를 모든 텐서로 선형으로 확장합니다.보다 으로는 단순한 텐서 상에서 p End ( V) ( p) \ \^ { } { } \ { ( \ { p} V ) ,( \ k ) 를 정의할 수 있습니다.즉, A가 작용하게 될 k개의 성분을 선택한 다음 다른 선택에서 얻은 모든 결과를 요약한다.만약 p, k{\displaystyle p<, k}<, k=0{\textstyle\bigwedge ^{p}A^{k}=0 p}. ⋀ nV{\textstyle\bigwedge ^{n}V}기초 e1에1-dimensional은 ∧⋯ ∧ en{\displaystyle e_{1}\wedge \cdots \wedge e_{n}}, 우리는 한 k{\textstyle\bigwedge ^{n}A^{k}}wi에 대해 ⋀를 확인할 수 있⋀을 정의 내린다.ththe 고유번호 K K가 만족
- [ End pV ) { \{\}^{에 대해서는 외부 전치 T End ( n- V) \ \ ^{ { 를 정의합니다
- A ( ) { A \ {} ( )} 、 A A ) A (n - - ) style \ A \ detyle \ det A 。이러한 정의는 다른 버전과 동일합니다.
기본 속성
행렬식, 추적 및 인접의 다른 정의에서 얻은 모든 결과는 이 정의에서 얻을 수 있다(이러한 정의는 동일하기 때문에).다음은 이러한 새로운 정의와 관련된 몇 가지 기본 속성입니다.
- 는K {\ K선형입니다.
- 우리는 표준 동형성을 가지고 있다.단, V^{와n - V^{ 사이에는 표준 동형이 없습니다.
- 된 매트릭스 k \ \ {}의 엔트리는\ \ 입니다.
- 특히,그렇기 때문에
- 특히,
- 다항식 ( ) A ( ) \ { { } ( ) \ A \ {} ( )는 다음과 같이 구할 수 있습니다.유사하게,
레버리어 알고리즘
n \ \bigwedgek}는 다항식의 n- {t)^{항계수이다그들은 또한(⋀ n− 1p)T{\textstyle \left(\bigwedge ^{n-1}A^{p}\right)^{\mathrm{T}의 표정에}}와 엔(adj )k{\textstyle\bigwedge ^{n}(\operatorname{adj}A)^{k}}⋀. k{\textstyle\bigwedge ^{n}A^에 대해 ⋀ 컴퓨팅의 르베리에의 Algorithm[20]은 경제적인 방법이 나타나고 있다.{k} 및 - A \ \ bigwedge ^ { A^k :
- n - 0 { \ ^ { n - }
- k -, n- 2, , , , { k =, , \, 의 ,
물리
물리학에서는 많은 양이 교대로 연산자에 의해 자연스럽게 표현된다.예를 들어 하전 입자의 움직임이 4차원 시공간에서의 속도와 가속도 벡터에 의해 설명된다면, 속도 벡터의 정규화를 위해서는 전자력이 속도상의 교대 연산자여야 한다.이것의 6가지 자유도는 전기장과 자기장과 동일하다.
선형 형상
분해 가능한 k 벡터는 기하학적 해석을 가지고 있다: 쌍벡터 u v v는 변 u와 v가 있는 방향성 평행사변형의 면적에 의해 주어진 벡터에 의해 "가중치된" 평면을 나타낸다. 유추적으로, 3벡터 u v v w w는 방향성 평행사변형의 가장자리에 의해 가중치가 부여된 3공간이다., v 및 w.
투영 형상
V {^{의 분해 가능한 k 벡터는 V의 가중치 k차원 선형 서브스페이스에 해당한다.특히, Gr(V)로 표시된k V의 k차원 부분공간의 그래스마니안은 투영 Pk 의 대수적 부분변수로 자연스럽게 식별될 수 있다(\ P\left이것은 플뤼커 매립이라고 불립니다.
미분 지오메트리
외부 대수는 미분 [21]형태를 정의하는 데 사용되는 미분 기하학에서 주목할 만한 응용 분야를 가지고 있습니다.미분 형태는 벡터의 길이, 평행사변형의 영역, 고차원 물체의 부피를 평가하는 수학적 객체입니다. 따라서 그것들은 곡선, 표면 및 고차원 다지관에 걸쳐 미적분으로부터 선 적분 및 표면 적분을 일반화하는 방식으로 통합될 수 있습니다.미분 가능한 다양체의 한 점에서의 미분 형태는 그 점에서의 접선 공간상의 교대 다선형 형태이다.마찬가지로, 차수 k의 형태는 접선 공간의 k번째 외부 검정력에 대한 선형 함수이다.그 결과, 다선형 형태의 외적물은 미분 형식의 자연 외적물을 정의한다.미분 형태는 미분 기하학의 다양한 영역에서 중요한 역할을 합니다.
특히, 외부 도함수는 다지관상의 미분 형식의 외부 대수에 미분 등급 대수의 구조를 부여한다.외부 도함수는 매니폴드 간의 부드러운 매핑을 따라 풀백과 일치하므로 자연 미분 연산자입니다.외부 도함수를 갖춘 미분 형식의 외부 대수는 코호몰로지가 기본 다양체의 de Rham 코호몰로지라고 불리는 코체인 복합체이며 미분 가능 다양체의 대수적 위상학에서 중요한 역할을 한다.
표현 이론
표현 이론에서, 외부 대수는 벡터 공간의 범주에서 두 개의 기본적인 슈어 함수 중 하나이며, 다른 하나는 대칭 대수이다.이러한 구성은 일반 선형 그룹의 축소 불가능한 표현을 생성하기 위해 사용됩니다. 기본 표현을 참조하십시오.
초공간
복소수 위의 외부 대수는 페르미온과 초대칭에 관련된 물리 이론에서 기본적인 역할을 하는 슈퍼 대수의 전형적인 예입니다.외부 대수의 단일 요소는 슈퍼넘버[22] 또는 그래스만 수라고 불립니다.외부대수 자체는 1차원 초공간일 뿐입니다.외부대수의 모든 점들의 집합일 뿐입니다.이 공간의 토폴로지는 기본적으로 약한 토폴로지이며, 열린 집합은 실린더 집합입니다.n차원 초공간은 외부 대수의 n배 산물이다.
리 대수 호몰로지
L을 필드 K 위의 Lie 대수로 하면, L의 외부 대수에 연쇄 복합체의 구조를 정의할 수 있다.이것은 K-선형 매핑입니다.
분해 가능한 원소에 정의되다
야코비 항등식은 θθ = 0인 경우에만 유지되며, 따라서 이것은 반교합 비연관대수 L이 리 대수가 되기 위해 필요하고 충분한 조건이다., 이 경우 L L은 경계 연산자 θ를 가지는 체인 복합체이다.이 복합체와 관련된 호몰로지는 리 대수 호몰로지이다.
호몰로지 대수
외부대수는 호몰로지 대수학의 기본 대상인 코스줄 복합체를 구성하는 데 있어 주요 요소이다.
역사
외부대수는 1844년 헤르만 그라스만에 의해 Ausdehnungslehre, 즉 [23]확장 이론이라는 포괄적 용어로 처음 도입되었다.이것은 더 일반적으로 확장된 양의 대수(또는 자명한) 이론을 언급했고 벡터 공간의 현대적 개념의 초기 선구자 중 하나였다.생베낭은 또한 그라스만보다 [24]우선시하는 외부 미적분에 대한 비슷한 생각을 발표했다.
대수학 자체는 케일리와 실베스터의 다차원 이론의 형식적인 측면을 포착하는 일련의 규칙 또는 공리로 만들어졌습니다.따라서 그것은 기하학적 [25]관점에서 형식적 추론의 작업에만 초점을 맞춘 것을 제외하면 명제적 미적분학과 매우 유사했다.특히, 이 새로운 개발은 이전에는 좌표 관점에서만 조사되었던 특성인 차원의 자명한 특성화를 가능하게 했다.
벡터와 다중 벡터의 새로운 이론은 1888년 주세페 페아노에 의해 철저히 조사되기 전까지 19세기 중반의 [26]수학자들에게서 사라졌다.페아노의 업적은 또한 프랑스 기하학 학파(특히 앙리 푸앵카레, 엘리 카르탕, 가스통 다르부)가 그라스만의 사상을 미적분학에 적용하면서 그 주제가 통일된 세기가 바뀔 때까지 다소 모호하게 남아있었다.
잠시 후, 알프레드 노스 화이트헤드는 페아노와 그라스만의 아이디어를 빌려 그의 보편대수를 도입했다.그리고 이것은 대수체계의 자명한 개념을 확고한 논리적 기반 위에 놓음으로써 추상대수의 20세기 발전을 위한 길을 열었다.
「 」를 참조해 주세요.
- 외부 미적분 아이덴티티
- 교대 대수
- 대칭대수, 대칭유사체
- 클리포드 대수, 0이 아닌 2차 형식을 사용한 외부 대수의 일반화
- 와일 대수, 심플렉틱 형식에 의한 대칭 대수의 양자 변형
- 다선형 대수
- 텐서 대수
- 기하학 대수
- 코스줄 콤플렉스
메모들
- ^ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- ^ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 83. ISBN 0-7167-0344-0.
- ^ Grassmann(1844)은 이것을 확장 대수로 소개했다.클리포드 1878).그는 단지 그가 정의한 생산물을 나타내기 위해 외적물(outher, outside)이라는 단어를 사용했다. 오늘날에는 외적물이라고 불리며, 아마도 현대 선형대수에서 정의된 외적물과 구별하기 위해서이다.
- ^ 엄밀히 말하면, 그 크기는 어떤 추가적인 구조, 즉 벡터가 유클리드 공간에 있다는 것에 달려 있다.우리는 주제에 대한 직관을 개발하는 데 도움이 되는 경우를 제외하고는 일반적으로 이 구조가 이용 가능하다고 가정하지 않는다.
- ^ k-벡터라는 용어는 4차원 벡터 공간의 요소를 의미할 수 있는 4-벡터와 같은 유사한 용어와 동일하지 않으며 혼동되어서는 안 된다.소수의 저자들은 k-벡터 대신 k-멀티벡터라는 용어를 사용하므로 이러한 혼동을 피할 수 있다.
- ^ 이 영역의 공리화는 레오폴드 크로네커와 칼 바이얼스트라스 때문이다. 부르바키(1989b, 역사주)를 참조하라.최신 치료법에 대해서는 Mac Lane & Birkhoff(1999, Oremi IX.2.2)를 참조하십시오.기초 처치에 대해서는 Stren(1993년, 5장)을 참조하십시오.
- ^ Mac Lane & Birkhoff (1999년)
- ^ 이것의 증거는 부르바키(1989)에서 보다 일반적인 것에서 찾을 수 있다.
- ^ Sternberg(1964, § III.6)를 참조한다.
- ^ 부르바키(1989년, § III.7.1), 맥 레인 & 버크호프(1999년, 정리 16.6.8)를 참조한다.보편적 재산에 대한 자세한 내용은 Mac Lane & Birkhoff(1999년, 제6장)와 Bourbaki의 작품을 통해 확인할 수 있습니다.
- ^ 일반화는 부르바키(1989년, § III.7.5)를 참조한다.
- ^ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- ^ 참고: 여기에 표시된 방향은 정확하지 않습니다. 다이어그램은 모든 k-양식에 대해 방향이 정의되어 있다는 느낌을 줄 뿐입니다.
- ^ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 58–60, 83, 100–109, 115–119. ISBN 0-7167-0344-0.
- ^ 실제로, V의 외부 대수는 V 위의 아벨리안 리 초대수 구조의 포섭 대수이다.
- ^ 또한 V와 W가 교환 링 상의 모듈인 경우에도 이 부분은 더 일반적입니다.이는 에피모피즘을 에피모피즘으로 변환합니다.Bourbaki(1989, Proposition 3, § III.7.2) 참조.
- ^ 이 문장은 V와 W가 교환 링을 통해 투영 모듈인 경우에만 일반화합니다.그렇지 않으면 일반적으로 \ \ 가 단형을 단형으로 변환하지 않습니다.부르바키(1989년, 발의안 제12호, 제III.7.9조)를 참조한다.
- ^ 이러한 여과는 벡터 번들 및 교환 링 상의 투영 모듈에도 적용됩니다.따라서 모든 짧은 정확한 시퀀스가 다른 아벨 범주에서 분할되는 것은 아니기 때문에 이것은 직합에 대해 위에서 인용한 결과보다 더 일반적이다.
- ^ S.Winitzki, 외부 제품을 통한 선형 대수학, https://sites.google.com/site/winitzki/linalg
- ^ W.Kahan(2009), 요르단의 정상형.https://www.cs.berkeley.edu/~wkahan/MathH110/jordan.pdf
- ^ James, A. T. (1983). "On the Wedge Product". In Karlin, Samuel; Amemiya, Takeshi; Goodman, Leo A. (eds.). Studies in Econometrics, Time Series, and Multivariate Statistics. Academic Press. pp. 455–464. ISBN 0-12-398750-4.
- ^ Bryce DeWitt, Supermanifolds, (1984) 케임브리지 대학 출판사 ISBN 0-521-42377-5(1장 1페이지 참조)
- ^ Kannenberg(2000)는 Grassmann의 작품을 영어로 번역하여 Ausdehnungslehre를 확장 이론으로 번역하였다.
- ^ J Itard, 과학 전기 사전(뉴욕 1970~1990)
- ^ 저자들은 과거에 이 미적분을 확장의 미적분(Whitehead 1898; Forder 1941), 또는 광범위한 대수(Clifford 1878)라고 다양하게 언급했고 최근에는 확장 벡터 대수(Browne 2007)라고 불렀다.
- ^ 부르바키 1989, 페이지 661
레퍼런스
수학적 참고 자료
- Bishop, R.; Goldberg, S. I. (1980), Tensor analysis on manifolds, Dover, ISBN 0-486-64039-6
- 이 글에서 채택한 관점에서의 Hodge 이중성에 대한 자세한 설명뿐만 아니라 교대 텐서 및 교대 형식의 처리도 포함합니다.
- Bourbaki, Nicolas (1989), Elements of mathematics, Algebra I, Springer-Verlag, ISBN 3-540-64243-9
- 이것이 그 기사의 주된 수학적 참고 자료이다.교환환에 대한 모듈의 외부 대수를 소개합니다(단, 이 기사는 주로 링이 필드인 경우에 특화되어 있지만). 여기에는 유니버설 속성, 펑터빌리티, 이중성 및 바이알 대문자 구조에 대한 설명이 포함됩니다.§ III.7 및 § III.11을 참조한다.
- Bryant, R. L.; Chern, S. S.; Gardner, R. B.; Goldschmidt, H. L.; Griffiths, P. A. (1991), Exterior differential systems, Springer-Verlag
- Mac Lane, S.; Birkhoff, G. (1999), Algebra, AMS Chelsea, ISBN 0-8218-1646-2
- 16장 6-10절에서는 이중성, 결정식 및 미성년자, 교대 형식을 포함한 외부 대수에 대한 보다 기본적인 설명을 제공한다.
- Sternberg, Shlomo (1964), Lectures on Differential Geometry, Prentice Hall
- 외부 대수를 교대 텐서로서 고전적으로 처리하고 미분 기하학에 대한 응용 프로그램을 포함합니다.
이력 레퍼런스
- Bourbaki (1989, Historical note on chapters II and III)
- Clifford, W. (1878), "Applications of Grassmann's Extensive Algebra", American Journal of Mathematics, The Johns Hopkins University Press, 1 (4): 350–358, doi:10.2307/2369379, JSTOR 2369379
- Forder, H. G. (1941), The Calculus of Extension, Internet Archive
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre – Ein neuer Zweig der Mathematik (in German) (선형 확장 이론 – 수학의 새로운 분과) 대체 참조
- Kannenberg, Lloyd (2000), Extension Theory (translation of Grassmann's Ausdehnungslehre), American Mathematical Society, ISBN 0-8218-2031-1
- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva; 를 참조해 주세요.
- Whitehead, Alfred North (1898), A Treatise on Universal Algebra, with Applications, Cambridge
기타 참고 자료 및 추가 자료
- Browne, J. M. (2007), Grassmann algebra – Exploring applications of Extended Vector Algebra with Mathematica
- 응용 분야에 초점을 맞춘 외부 대수 및 기하 대수 입문.또한 역사 섹션과 참고 문헌 목록도 포함됩니다.
- Spivak, Michael (1965), Calculus on manifolds, Addison-Wesley, ISBN 978-0-8053-9021-6
- 외부 대수의 미분 형태, 특히 적분 및 Stokes의 정리에 초점을 맞춘 적용을 포함합니다.이 텍스트에서 " V 는 V 상에서 k-폼을 번갈아 하는 공간을 의미합니다.즉, Spivak k의 경우, 이 문서에서는 "^{라고 부릅니다엔덤 4
- Strang, G. (1993), Introduction to linear algebra, Wellesley-Cambridge Press, ISBN 978-0-9614088-5-5
- 부호 있는 영역, 볼륨 및 고차원 볼륨으로서의 결정 인자의 공리화에 대한 기본적인 처리를 포함합니다.
- Onishchik, A.L. (2001) [1994], "Exterior algebra", Encyclopedia of Mathematics, EMS Press
- 웬델 H.플레밍(1965) 여러 변수의 함수, 애디슨 웨슬리.
- 6장: 외부 대수와 미분학, 205-38페이지.다변량 미적분학의 이 교과서는 대학의 미적분 시퀀스에 미분 형식의 외부 대수를 능숙하게 소개한다.
- Winitzki, S. (2010), Linear Algebra via Exterior Products
- 외부 곱을 사용한 기본 유한 차원 선형 대수에서의 좌표 자유 접근법 소개.
- Shafarevich, I. R.; Remizov, A. O. (2012). Linear Algebra and Geometry. Springer. ISBN 978-3-642-30993-9.
- 제10장:외부 제품 및 외부 대수학
- "사영 기하학의 그래스만 방법" Cesare Burali-Forti가 사영 기하학에 외부 대수의 적용에 대해 세 개의 음표로 이루어진 영어 번역본
- C. Burali-Forti, "H. Grassmann의 방법에 따른 미분 기하학 입문" 외부 대수의 기하학적 응용에 관한 초기 책의 영어 번역
- "연장 이론의 원리에 따른 기계" 외부 대수의 응용에 관한 그라스만의 논문의 영어 번역





 대하여
대하여 


 단위
단위 











 x
x




 =
=



























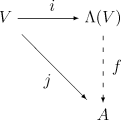

 텐서대수 T(M)의 적절한 몫으로 정의할 수 있다.그것은 유사한 보편적 성질을 만족시킬 것이다.require
텐서대수 T(M)의 적절한 몫으로 정의할 수 있다.그것은 유사한 보편적 성질을 만족시킬 것이다.require






![{\displaystyle (t~{\widehat {\otimes }}~s)^{i_{1}\cdots i_{r+p}}=t^{[i_{1}\cdots i_{r}}s^{i_{r+1}\cdots i_{r+p}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3a6e1f0d329e0d2883efe13d67dc45065142bba)
 랭크 r의 반대칭 텐서라고
랭크 r의 반대칭 텐서라고 







 존재합니다. 이
존재합니다. 이






























 (는) 정의되어 있는2개의 l-param입니다.
(는) 정의되어 있는2개의 l-param입니다.





 상대적 순서는 riffle shuffle로 유지됩니다.riffle shuffle은 순서가 매겨진 시퀀스를 왼쪽과 오른쪽의 2개의 순서로 분할하기만 하면 됩니다.
상대적 순서는 riffle shuffle로 유지됩니다.riffle shuffle은 순서가 매겨진 시퀀스를 왼쪽과 오른쪽의 2개의 순서로 분할하기만 하면 됩니다. 




 균질도를 유지합니다.분해 가능한 요소에 대한
균질도를 유지합니다.분해 가능한 요소에 대한 



 (가) 벡터 공간의
(가) 벡터 공간의 



















 만족
만족








 엔트리는
엔트리는





















![\partial (x_1\wedge\cdots\wedge x_{p+1}) = \frac{1}{p+1}\sum_{j<\ell}(-1)^{j+\ell+1}[x_j,x_\ell]\wedge x_1\wedge\cdots\wedge \hat{x}_j\wedge\cdots\wedge\hat{x}_\ell\wedge\cdots\wedge x_{p+1}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/78a74a56321a71b4e71d78158149d5c833f7a56e)
 경계 연산자 θ를
경계 연산자 θ를