각속도
Angular velocity| 각속도 | |
|---|---|
공통 기호 | ω |
| SI 기준 단위 | s−1. |
| 광범위? | 네. |
| 집약적? | 있음(강체만 해당) |
| 보존? | 아니요. |
아래의 동작 좌표 변환 | 의사 벡터 |
파생상품 기타 수량 | ω = d520 / dt |
| 치수 | |
| 시리즈의 일부 |
| 고전 역학 |
|---|
물리학에서 각속도 또는 회전속도(θ 또는 δ)는 각주파수 [1]벡터라고도 하며, 물체의 각도 위치 또는 방향이 시간에 따라 얼마나 빨리 변하는지를 나타내는 의사벡터 표현이다(즉, 물체가 점이나 축에 대해 얼마나 빨리 회전하는지).의사벡터의 크기는 물체가 회전하거나 회전하는 속도인 각 속도를 나타내며, 그 방향은 회전의 순간 평면 또는 각 변위에 대해 정규적입니다.각 속도의 방향은 일반적으로 오른손 [2]법칙에 의해 지정된다.
각속도에는 두 가지 유형이 있습니다.
- 궤도 각속도는 점 물체가 고정된 원점을 중심으로 얼마나 빨리 회전하는지, 즉 원점에 대한 각도 위치의 시간 변화 속도를 의미한다.
- 스핀각속도는 강체가 회전 중심에 대해 얼마나 빨리 회전하는지를 말하며 궤도각속도와는 대조적으로 원점 선택과는 무관하다.
일반적으로 각속도에는 단위시간당 각도의 치수가 있습니다(직선속도로부터의 거리를 공통의 시간으로 치환하는 각도).각 속도의 SI 단위는 [3]초당 라디안이며, 라디안은 무차원 양이므로 각 속도의 SI 단위는 s로 표시될−1 수 있다.각속도는 보통 오메가 기호(,, 때로는 ω)로 표현된다.관례상 양의 각속도는 반시계방향 회전을 나타내고 음의 각속도는 시계방향 회전을 나타냅니다.
예를 들어 정지 위성은 적도 상공에서 하루에 1회 궤도, 즉 24시간마다 360도 궤도를 완성하며, 각속도 θ = (360°)/ (24h) = 15°/h 또는 (2µ rad)/ (24h) 26 0.26rad/h이다.각도를 라디안 단위로 측정할 경우 선형 속도는 반지름에 각 속도를 r { v입니다. 따라서 지구 중심에서 궤도 반지름이 42,000km일 때 위성의 우주 통과 속도는 v = 42,000km × 0.26/h ≈ 11,000km/h이다.위성이 지구의 자전과 함께 동쪽으로 이동하기 때문에(북극 위에서는 시계 반대 방향으로) 각 속도는 양수입니다.
점입자의 궤도 각속도
2차원 입자

x축으로부터의 각도 에 의해 주어진 위치를 갖는 r {\r에서의 가장 단순한 원운동의 경우, 궤도 각속도는 시간에 대한 각도 변화율이다: = d d textstyle \ { phi } { d } { }} 。\은 라디안 단위로 측정되며, 원 주위의 양의 x축에서 입자까지의 호 길이는 이며, 선형 속도는 ( ) = r ( ) { v) =rac\= { 입니다
평면 내에서 움직이는 입자의 일반적인 경우, 궤도 각 속도는 선택된 원점에 대한 위치 벡터가 "스위프 아웃" 각도로 이동하는 속도입니다.이 다이어그램은 O(\ O에서 P(\ P까지의 위치 r(\과 극좌표를 나타내고 있습니다. (모든 변수는 t(\ t의 함수입니다.)입자는 v δ + δ \ \+ \ 선형 속도 분할을 가지며, 반경 vδ \_ {\\}}}} 은 반지름 및 교차 에 평행합니다erp}}: 반지름에 입니다.반지름 성분이 없는 경우 입자는 원점을 중심으로 이동하지만, 교차 반지름 성분이 없는 경우 원점에서 직선으로 이동합니다.반지름 운동은 각도를 변경하지 않기 때문에 선형 속도의 교차 반지름 성분만 각 속도에 기여합니다.
각속도 θ는 시간에 대한 각위치 변화율이며, 이는 다음과 같이 교차 방사 속도로부터 계산할 수 있다.
여기서 크로스 레이디얼 vµ {\}}는 부호화된 크기 vµ {\ _입니다. 반시계 방향 이동에는 양의 값, 시계 방향에는 음의 값입니다.선형 v {\에 대한 극좌표를 취하면 반지름 벡터에 대한 v {\v}(선형 속도) 및 각도 {\ \}(\ })가 됩니다. 이러한 관점에서 는 과 같습니다.
공식은 r ( cos ( ) , sin ( )\ r}= ( r \ cos ( \ varphi ) , r \ ( \ )} , r \ r } } } } } } of of of of of of of of of of of of of } of of of of of } of of } these of of these r these these of of of of of으로 d t ( - r sin 、 sin( + { \ } { d } { \ ( ) - 、 + ) ( \ { ( \ ( \ { r } ( \ )d {\frac {= {dt} } {dot } }을 있으면 r {{r은 반경 단위 벡터이고 수직 성분은 r {r 로 됩니다.^ { { { varphi은는) 수직 단위 벡터이기 때문에 r { }} 입니다.
2차원에서 각속도는 방향을 나타내는 플러스 또는 마이너스 기호가 있는 수치이지만 방향을 가리키지는 않습니다.일반적으로 부호는 반지름 벡터가 시계 반대 방향으로 돌면 양수, 시계 반대 방향으로 돌면 음수로 간주됩니다.각속도는 의사척도로 불리며 한쪽 축을 반전시키거나 두 축을 전환하는 등 패리티 반전 하에서 부호를 변경하는 수치이다.
3차원 입자
3차원 공간에서 우리는 다시 움직이는 입자의 위치 벡터 r을 갖게 된다.여기서 궤도각속도는 r이 각도를 소거하는 속도이며, 그 방향이 r이 각도를 소거하는 순간 평면(즉, r과 v에 의해 스판되는 평면)에 수직인 의사벡터이다.단, 어떤 평면에 수직인 두 가지 방향이 있기 때문에 각속도 방향을 고유하게 특정하기 위한 추가 조건이 필요하며, 기존에는 오른손 법칙을 사용한다.
의사 u {\을(를) r 및 v로 스판되는 평면에 수직인 단위 벡터로 하여 오른쪽 규칙을 만족하도록 합니다(즉, 각도 변위의 순간 방향이u {\ 위에서 반대 방향임).위의 2차원 사례와 같이 이 평면에서 , ) {(r,\를 취하면 궤도 각속도 벡터를 다음과 같이 정의할 수 있다.
여기서 θ는 r과 v 사이의 각도입니다.교차곱의 관점에서 보면 다음과 같습니다.
위의 방정식을 통해 접선 속도를 다음과 같이 복구할 수 있습니다.
각속도 벡터 추가
외부 에 대해 회전각속도 로 회전하는 F1({1})에서 점의 회전중심을 displaystyle로 회전하는 경우, w는 1 + θ _{ _를 F2에 대한 회전중심점 주변의 점의 합성 궤도각속도 벡터가 되도록 정의할 수 있다. 이 연산은 통상적인 벡터 덧셈과 일치하며, 진정한 v의 대수구조와 같은 각속도를 제공한다.엑터(extor)가 아니라 그냥 의사일 뿐이죠
위의 덧셈의 유일한 명백한 특성은 교환성이다.이는 속도 텐서 W(아래 참조)가 스큐-텐서이므로 R W {\ R는 R + t + ( W t ) +the { \ R + \ + { \ 1 {2 ( + 로 확장 가능한 회전행렬이다.}\ dtW_{1는 첫 번째 순서와 교환하므로 1 + 2 1 \ 1
또한 감산은 음의 벡터의 덧셈으로도 정의됩니다.
강체 또는 기준 프레임의 회전각 속도
3개의 단위 좌표 벡터가 회전하는 프레임이 주어졌을 때, 3개 모두 각 순간의 각속도가 동일해야 합니다.이러한 프레임에서 각 벡터는 일정한 스칼라 반경을 가진 이동 입자로 간주할 수 있다.
회전 프레임은 강체의 맥락에서 나타나며, 이를 위해 특수 공구가 개발되었습니다. 즉, 스핀 각 속도는 벡터 또는 텐서로 설명할 수 있습니다.
일반적인 정의와 일관되게 프레임의 스핀 각 속도는 회전 중심에 대한 세 벡터 중 하나의 궤도 각 속도로 정의된다.프레임에 대한 각속도 벡터의 추가는 일반적인 벡터 추가(선형 이동의 구성)로도 정의되며 짐벌에서처럼 회전을 분해하는 데 유용합니다.벡터의 모든 성분은 이동 프레임을 정의하는 파라미터의 도함수(Uler 각도 또는 회전 행렬)로 계산할 수 있습니다.일반적인 경우와 마찬가지로 덧셈은 ut + 2 2 + 1\ style \ {1 + \ _ {2 \ _ {1}= \ obega _ {2} + \ _ {1 입니다.
오일러의 회전정리에 따르면 회전하는 프레임은 각속도 벡터의 방향인 순간회전축을 가지며 각속도 크기는 2차원 경우와 일치한다.
강체에 고정된 Rstyle\을 선택하면 차체 내 모든 지점의 r이 다음과 같이 지정됩니다.
본체 고정 프레임의 기본 벡터의 구성요소
고정된 점 O를 중심으로 회전하는 강체를 고려합니다.벡터 style 의 직교 정규 세트로 구성된 기준 프레임을 본체에 구축합니다.O에 대한 프레임과 본체의 각속도 벡터는 다음과 같습니다.
서 e t{ { dot \ } _ { } = i ,, ,{ \ } { i } = 1, 2} { } { = 1,까지의 프레임 입니다.
이 공식은 식과 호환되지 않습니다.
이 공식은 프레임 또는 강체에 적용되는 반면, 이 섹션의 공식은 O에 대한 단일 지점의 각 속도만 정의하기 때문이다.강체의 경우 단일 스타일mega이 체내 모든 입자의 움직임을 설명해야 합니다.
오일러 각도의 성분
스핀 각속도 유사 벡터의 성분은 레온하르트 오일러가 오일러 각도와 중간 프레임을 사용하여 처음 계산했다.
- 기준 프레임의 1축(세차축)
- 기준 프레임에 대한 이동 프레임의 노드 라인(너테이션 축)
- 이동 프레임의 한 축(내부 회전 축)
오일러는 이 세 개의 축 각각에 대한 각속도 유사 벡터의 투영이 연관된 각도의 도함수라는 것을 증명했다. (이것은 순간 회전을 세 개의 순간 오일러 회전으로 분해하는 것과 같다.)그 [5]때문에,
이 베이스는 직교적인 것이 아니라 사용하기 어렵지만 이제 베이스 변경만으로 속도 벡터를 고정 프레임이나 이동 프레임으로 변경할 수 있습니다.예를 들어 모바일프레임으로의 변경은 다음과 같습니다.
서 i ^, {{\hat { {\은 이동체에 고정된 프레임의 단위 벡터입니다.이 예는 오일러 [citation needed]각도에 대한 Z-X-Z 규칙을 사용하여 만들어졌습니다.
텐서
위에서 정의한 각속도 벡터 ( x , y , z) {{\ _ _는 다음과 같이 각속도 텐서로서 동등하게 표현될 수 있다. 행렬(또는 선형 매핑) W = W(t)
이것은 극소 회전 행렬입니다.선형 매핑 W는 (as × ) {}}\로 동작합니다.
방향 매트릭스에서 계산
고정 축을 중심으로 균일한 원형 운동을 하는 r \{r은 다음을 만족합니다.
이동 직교 좌표 _},\ { _{3인 프레임의 방향행렬 A(t)가 주어지면 각속도 텐서 W(t)를 다음과 같이 구할 수 있다.각 속도는 세 벡터 \ =\ _에 대해 동일해야 합니다. 따라서 세 벡터 방정식을 행렬의 열에 배열하면 다음과 같습니다.
(이것은 A(t)가 균일하게 회전하지 않아도 유지됩니다.)따라서 각속도 텐서는 다음과 같다.
의 역행렬 A(\ A는 A이기 때문이다.
특성.
일반적으로 n차원 공간에서의 각속도는 두 번째 등급 스큐-대칭 텐서인 각변위 텐서의 시간파생물이다.
이 텐서 W는 n(n-1)/2개의 독립 성분을 가질 것이며, 이는 n차원 내부 곱 [6]공간의 회전의 Lie 그룹의 Lie 대수의 차원이다.
속도 벡터에 대한 이중성
3차원에서는 2등급 텐서가 3차원에서는 의사벡터와 이중이기 때문에 각속도는 의사벡터로 나타낼 수 있다.각속도 텐서 W = W(t)는 스큐-변형 행렬이기 때문에:
호지 쌍은 벡터이며, 이는 정확히 이전의 각속도 [ x , y , z {\{\ { __{이다.
W의 지수
초기 프레임 A(0)를 알고 일정한 각속도 텐서 W가 주어지면 주어진 t에 대해 A(t)를 얻을 수 있다.행렬 미분 방정식을 호출합니다.
이 방정식은 다음과 같이 통합될 수 있습니다.
이는 회전의 Lie 그룹과의 연결을 나타냅니다.
W는 스큐대칭입니다.
우리는 각 속도 텐서가 스큐 대칭이라는 것을 증명한다.이(가) T -W {\{}를 충족합니다.
회전행렬 A는 전치와는 반대인 직교이므로 \ I \ A^ { \ { \ text} A (t) { A 의 , 방정식의 시간 도함수를 취하면 다음과 같이 됩니다.
공식( B) T {\
따라서 W는 전치선의 음수이며, 이는 왜곡 대칭임을 의미합니다.
코디네이트 프리 설명
임의의 t{\ t에서 각속도 텐서는 원점을 중심으로 회전하는 강체상의 점의 위치 r t와 v의 선형 지도를 나타낸다.
이 선형 지도와 각속도 의사벡터(\의 관계는 다음과 같습니다.
W는 직교 변환의 도함수이기 때문에, 쌍선형 형태는
스큐가 되어 있습니다.따라서 우리는 외부 대수의 2에 다음과 같은 한 선형 형식L2}V이 있다는 사실을 적용할 수 있다.
서 r s V \ \ \r s의 외부 곱입니다.
L의 샤프♯ L을 취하면 얻을 수 있다.
L의♯ Hodge dual로서 : ( L ) : ( \ style \ \ } : ( { \ sharp )를 소개하고, 바람직한 단위 3-display 하여 Hodge dual의 정의를 2회 적용한다.
어디에
정의상.
는 임의의 벡터이므로 스칼라 곱의 비이성으로부터 다음과 같이 됩니다.
벡터장으로서의 각속도
강체의 스핀 각속도 텐서는 강체 내(강체 내) 속도에 매핑되는 선형 변환이므로 상수 벡터장으로 간주할 수 있다.특히 스핀각속도는 3차원 회전군 SO(3)의 라이 대수 SO(3)의 원소에 속하는 킬링 벡터장이다.
또한 스핀각속도 벡터장이 강체의 직선속도 벡터장 v(r)의 컬의 정확히 절반임을 알 수 있다.기호에서는
강체에 관한 고려 사항
회전하는 강체에 대한 각 속도에 대한 동일한 방정식을 얻을 수 있습니다.여기서 강체가 원점 주위를 회전한다고 가정하지 않는다.대신, 각 순간마다 선형 속도 V(t)로 움직이는 임의의 점 주위를 회전한다고 가정할 수 있습니다.
방정식을 얻으려면 프레임에 부착된 강체를 상상하고 강체에 대해 고정된 좌표계를 고려하는 것이 편리합니다.그런 다음 이 좌표와 고정 "실험실" 시스템 사이의 좌표 변환을 연구한다.
오른쪽 그림과 같이 실험실 시스템의 원점은 O점이고 강체 시스템의 원점은 O and이며 O is에서 O is까지의 벡터는 R이다.강체 중의 입자 i는 점 P에 위치하고 있으며, 이 입자의 벡터 위치는 랩 프레임 내에서는 R이며, 본체 프레임 내에서는 r 위치에i 있다i.입자의 위치는 다음과 같이 기록될 수 있습니다.
강체의 명확한 특징은 강체의 두 점 사이의 거리가 시간에 따라 변하지 않는다는 것이다., 벡터 의 길이는 변하지 않습니다.오일러의 회전정리에 의해 벡터 i {\를 o {\ { 로 할 수 있습니다. 서R {\{은 3×3 이고 r의 입니다e는 일정한 시점에 t = 0이라고 합니다.이 는 이제 회전 행렬 R(\만 변경되고 강체가 O점 중심으로 회전하므로 기준 벡터 \r} _가 아니기 때문에 유용합니다.또한 회전행렬의 세 열은 강체와 함께 회전하는 기준 프레임의 세 버서(versor)를 나타내기 때문에 이제 모든 축에 대한 회전을 볼 수 있습니다. 반면 {\ _는 회전 축과 평행한 경우 회전하지 않습니다. 따라서 다음과 같습니다.수직인 축에 대한 회전(즉, 각속도 유사 벡터의 성분이 평행하게 보이지 않으며, 각 속도에 수직인 성분만 계산할 수 있음)입자의 위치는 다음과 같이 표시됩니다.
시간 도함수를 취하면 입자의 속도가 산출됩니다.
여기서i V는 (실험 프레임에서) 입자의 속도이고 V는 O†(강체 프레임의 원점)의 속도입니다.R {은 회전 이므로 그 역행렬은 전치입니다. 우리는 = R R { {{I } {R } ^{ \ {
또는
서 W R R { W = { {\} text은 이전의 각속도 텐서이다.
이것이 스큐 대칭 매트릭스임을 증명할 수 있으므로, 우리는 그 듀얼을 취하여 정확히 이전의 각속도 벡터인 3차원 의사 벡터를 수 있다 {\ {\ :
위의 속도식에 W를 θ로 대입하고 행렬 곱셈을 등가 교차곱으로 대입하면 다음과 같습니다.
강체 내 점의 속도는 강체에 고정된 기준점의 속도와 기준점에 대한 입자의 궤도 각 속도를 포함하는 교차 곱의 두 가지 용어로 나눌 수 있다.이 각속도는 물리학자들이 "원점 O"에 대한 기준점 O"의 궤도 각속도와는 대조적으로 강체의 "회전 각속도"라고 부르는 것입니다.
일관성.
우리는 강체가 임의의 점을 중심으로 회전한다고 가정해 왔다.우리는 이전에 정의된 스핀 각 속도가 원점 선택과 무관하다는 것을 증명해야 한다. 즉, 스핀 각 속도가 회전 강체의 고유 특성임을 의미한다.(원점 입자의 궤도 각속도와의 현저한 대비에 주목하십시오.)
오른쪽 그래프를 참조해 주세요.실험1 프레임의 원점은 O이고, O와2 O는 강체 위의 고정점 2개이며, 는 각각 v 1과 v({})입니다.O와2 O에 대한1 각속도를 각각 1 스타일 스타일 스타일로 가정합니다점 P와2 점 O는 단 하나의 속도이기 때문에
위의 두 가지는 다음을 산출한다.
점 P( 2는 임의이므로 다음과 같이 됩니다.
기준점이 순간 회전축인 경우 강체 내 점의 속도 표현은 각 속도 항만 갖는다.이는 순간 회전축의 속도가 0이기 때문이다.순간 회전축의 예로는 문의 경첩이 있습니다.또 다른 예는 순수하게 롤링하는 구형(또는 보다 일반적으로 볼록한) 강체의 접촉점이다.
「 」를 참조해 주세요.
레퍼런스
- ^ Cummings, Karen; Halliday, David (2007). Understanding physics. New Delhi: John Wiley & Sons Inc., authorized reprint to Wiley – India. pp. 449, 484, 485, 487. ISBN 978-81-265-0882-2.(UP1)
- ^ Hibbeler, Russell C. (2009). Engineering Mechanics. Upper Saddle River, New Jersey: Pearson Prentice Hall. pp. 314, 153. ISBN 978-0-13-607791-6.(EM1)
- ^ Taylor, Barry N. (2009). International System of Units (SI) (revised 2008 ed.). DIANE Publishing. p. 27. ISBN 978-1-4379-1558-7. 27페이지 발췌
- ^ Singh, Sunil K. "Angular Velocity". OpenStax. Rice University. Retrieved 21 May 2021.
- ^ K.S.HEDRIH: 레온하르트 오일러(1707–1783)와 강체역학
- ^ John Baez 웹사이트의 Classical Mechanics 페이지에 있는 회전과 각운동량, 특히 질문 1과 2.
- Symon, Keith (1971). Mechanics. Addison-Wesley, Reading, MA. ISBN 978-0-201-07392-8.
- Landau, L.D.; Lifshitz, E.M. (1997). Mechanics. Butterworth-Heinemann. ISBN 978-0-7506-2896-9.
외부 링크
- Arthur Lalanne Kimball의 대학 물리학 교과서 (입자의 각속도)
- Pickering, Steve (2009). "ω Speed of Rotation [Angular Velocity]". Sixty Symbols. Brady Haran for the University of Nottingham.



 의해 주어진 위치를 갖는
의해 주어진 위치를 갖는 











 .반지름 성분이 없는 경우 입자는 원점을 중심으로 이동하지만, 교차 반지름 성분이 없는 경우 원점에서 직선으로 이동합니다.반지름 운동은 각도를 변경하지 않기 때문에 선형 속도의 교차 반지름 성분만 각 속도에 기여합니다.
.반지름 성분이 없는 경우 입자는 원점을 중심으로 이동하지만, 교차 반지름 성분이 없는 경우 원점에서 직선으로 이동합니다.반지름 운동은 각도를 변경하지 않기 때문에 선형 속도의 교차 반지름 성분만 각 속도에 기여합니다. 
 부호화된 크기 v
부호화된 크기 v 대한 극좌표를 취하면 반지름 벡터에 대한
대한 극좌표를 취하면 반지름 벡터에 대한 
 됩니다. 이러한 관점에서
됩니다. 이러한 관점에서 





 반경 단위 벡터이고 수직 성분은 r
반경 단위 벡터이고 수직 성분은 r 


 (를) r 및 v로 스판되는 평면에 수직인 단위 벡터로 하여 오른쪽 규칙을 만족하도록 합니다(즉, 각도 변위의 순간 방향이
(를) r 및 v로 스판되는 평면에 수직인 단위 벡터로 하여 오른쪽 규칙을 만족하도록 합니다(즉, 각도 변위의 순간 방향이






 회전하는 경우, w
회전하는 경우, w F2
F2 R
R 
 첫 번째 순서와 교환하므로
첫 번째 순서와 교환하므로 
 선택하면 차체 내 모든 지점의
선택하면 차체 내 모든 지점의  다음과 같이 지정됩니다.
다음과 같이 지정됩니다.
 직교 정규
직교 정규 
 e
e  프레임
프레임  체내 모든 입자의 움직임을 설명해야 합니다.
체내 모든 입자의 움직임을 설명해야 합니다. 


 이동체에 고정된 프레임의 단위 벡터입니다.이 예는 오일러 [
이동체에 고정된 프레임의 단위 벡터입니다.이 예는 오일러 [ 다음과 같이 각속도 텐서로서 동등하게 표현될 수 있다. 행렬(또는 선형 매핑) W = W(t)
다음과 같이 각속도 텐서로서 동등하게 표현될 수 있다. 행렬(또는 선형 매핑) W = W(t)









![\boldsymbol\omega=[\omega_x,\omega_y,\omega_z]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)

 (가)
(가) 





 각속도 텐서는 원점을 중심으로 회전하는 강체상의 점의 위치
각속도 텐서는 원점을 중심으로 회전하는 강체상의 점의 위치  선형 지도를 나타낸다.
선형 지도를 나타낸다.












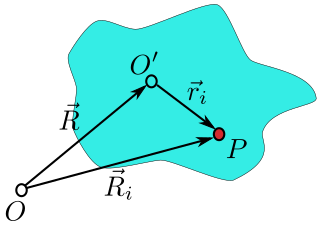

 길이는 변하지 않습니다.
길이는 변하지 않습니다.
 3×3
3×3 










 각각 v 1
각각 v 1 v
v