평면 입자 운동 역학
Mechanics of planar particle motion| 시리즈의 일부 |
| 고전 역학 |
|---|
이 문서에서는 비관성 [2][3][4]기준 프레임에서 관찰된 평면 운동[1] 상태의 입자에 대해 설명합니다.평면 운동의 가장 유명한 예는 중력적으로 서로 끌리는 두 구의 운동과 이 문제를 행성 [5]운동으로 일반화하는 것과 관련이 있다.원심력, 2체 문제, 궤도 및 케플러의 행성 운동 법칙을 참조하십시오.이러한 문제는 분석 역학,[6] 즉 주어진 힘의 법칙에서 궤도를 결정하는 일반적인 분야에 속합니다.이 기사는 평면 운동을 둘러싼 운동학적 문제, 즉 입자 궤적이 주어진 특정 궤적을 도출하는 데 필요한 힘의 결정에 더 초점을 맞추고 있다.여기서 가상의 힘으로 제시된 일반적인 결과는 여러 특정 비관성 프레임에서 볼 수 있는 이동 입자의 관찰에 적용됩니다. 예를 들어, 국부 프레임(하나는 움직이지 않는 것처럼 보이도록 움직이는 입자에 묶인 것)과 공회전 프레임(임의로 위치하지만 고정된 축과 회전 속도를 가진 것)e 입자는 반지름 운동과 0 방위 운동만 있는 것으로 보입니다).가공의 힘에 대한 라그랑주식 접근법이 도입되었다.
전자기력과 같은 실제 힘과 달리, 가상의 힘은 물체 사이의 물리적 상호작용에서 비롯되지 않는다.
가공의 힘을 이용한 해석
가상 힘의 출현은 일반적으로 비관성 기준 프레임의 사용과 관련이 있으며 관성 기준 프레임의 사용과 관련이 없다.관성 프레임과 가상의 힘(관성력 또는 의사 힘이라고도 함) 사이의 연결은 예를 들어 Arnol'[7]d로 표현된다.
비관성계의 운동 방정식은 관성력이라고 불리는 추가 항에 의해 관성계의 방정식과 다릅니다.이를 통해 시스템의 비관성 특성을 실험적으로 검출할 수 있습니다.
--
Iro는 [8]이 주제에 대해 약간 다른 방침을 제시한다.
두 기준 프레임의 불균일한 상대 운동으로 인한 추가 힘을 의사 힘이라고 합니다.
--
가상의 힘은 관성 기준 프레임의 운동 방정식에 나타나지 않습니다. 관성 프레임에서 물체의 운동은 실제 충격력에 의해 설명됩니다.그러나 회전 프레임과 같은 비관성 프레임에서는 실제 힘과 함께 가상의 힘이 포함된다면 뉴턴의 제1법칙과 제2법칙은 여전히 정확한 물리적 예측을 위해 사용될 수 있습니다.비관성 기준 프레임에서 역학의 문제를 해결하기 위해, 교과서에서 주어진 조언은 가상의 힘을 실제 힘처럼 다루고 관성 [9]프레임에 있는 것처럼 행동하라는 것입니다.<[10] >
가상의 힘을 실제 힘처럼 다루고 관성 프레임에 있는 것처럼 가정합니다.
--
"실제 힘처럼 가공의 힘을 취급하는 것"은 특히 특정 비관성 프레임에서 볼 수 있는 가공의 힘이 해당 프레임 내에서 이루어진 좌표 변환 아래의 벡터, 즉 실제 힘과 같은 벡터로서 변환된다는 것을 의미한다는 것을 언급해야 한다.
기준 개체 및 관찰 프레임 이동
다음으로 시간 가변 좌표가 관성 및 비관성 기준 프레임 모두에서 사용되므로 시간 가변 좌표를 사용하는 것은 관찰자의 변경과 혼동해서는 안 되며 관찰자가 선택한 설명의 변경일 뿐이다.이 점에 대한 자세한 설명과 그 주제에 대한 몇 가지 인용이 뒤따른다.
기준범위 및 좌표계
기준 프레임이라는 용어는 매우 넓은 의미로 자주 사용되지만, 현재 논의에서는 관찰자의 운동 상태, 즉 관성 기준 프레임 또는 비관성 기준 프레임을 가리키도록 그 의미가 제한된다.
좌표계라는 용어는 움직임을 기술하기 위한 변수 집합의 다른 가능한 선택들, 운동 상태에 관계없이 모든 관찰자가 사용할 수 있는 선택들 사이를 구별하는 데 사용됩니다.예를 들어 데카르트 좌표, 극좌표 및 (더 일반적으로) 곡선 좌표가 있습니다.
다음은 "운동 상태"와 "좌표계"[11][12]에 관한 두 가지 인용문입니다.
우리는 먼저 기준 프레임의 개념을 소개하는데, 그 자체는 관찰자의 생각과 관련이 있다: 기준 프레임은 어떤 의미에서는 "관찰자가 운반하는 비유클리드 공간"이다.좀 더 수학적인 정의를 내리겠습니다.참조 프레임은...관찰자의 강체 운동을 가진 유클리드 공간의 모든 점들의 집합.R로 된 프레임은 관찰자와 함께 움직인다고 합니다.원점 O의 좌표계 R을 설정하여 R을 기준으로 파티클의 공간 위치를 라벨링합니다({도끼의 해당 집합,}프레임 R{\displaystyle{\mathfrak{R}의 강체 운동 공유},}R{\displaystyle{\mathfrak{R}를 육체적인 실현}을 줄것을 액자 R{\displaystyle{\mathfrak{R}}}, 좌표 R에서 R'[해명 필요한] 가지고 다니며에 의해 변해 있다. 얼마나 자주'o'를에서 검토할 수 있을 것다고 각 인스턴트 o.에f 시간, 이 프레임의 물리적 양을 나타내기 위해 도입된 고유 물체(표준 및 텐서)의 구성요소에 대한 동일한 좌표 변환.
--
특수 상대성 이론과 일반 상대성 이론의 전통적인 발전에서는 상당히 다른 두 가지 생각을 구별하지 않는 것이 관례였다.첫 번째는 좌표계의 개념으로, 단순히 시공간 근방의 사건에 4개의 숫자를 매끄럽게, 반전할 수 있는 할당으로 이해된다.두 번째 기준 프레임은 그러한 숫자를 할당하는 데 사용되는 이상화된 시스템을 가리킵니다… 불필요한 제한을 피하기 위해, 우리는 이 배치를 운율의 개념과 분리할 수 있습니다.…우리의 목적에 있어서 특히 중요한 것은 각 기준 프레임이 시공간에서 발생하는 각 이벤트마다 일정한 운동 상태를 갖는 것입니다.…특수 상대성 이론의 맥락에서 그리고 우리가 관성 운동의 기준 프레임으로 스스로를 제한하는 한, 관성 기준 프레임과 그것이 유도하는 관성 좌표계 사이의 차이에 거의 의존하지 않는다.이러한 편안한 상황은 특수 상대성 이론 내에서조차 비균일한 움직임의 기준 프레임을 고려하기 시작하면 즉시 중단된다.…기준 프레임의 개념은 좌표계와 다른 구조로 다시 등장했습니다.
--
시간 가변 좌표계
일반좌표계에서 좌표에 대한 기저 벡터는 고정위치에서 시간적으로 변화하거나 고정시간에서의 위치에 따라 변화하거나 둘 다 변화할 수 있다.관성 프레임과 비관성 프레임에 부착된 좌표계는 시간, 공간 또는 둘 다에서 다양한 기저 벡터를 가질 수 있다는 점에 주목해야 한다. 예를 들어 관성 프레임에서 [13]볼 수 있는 극좌표 궤적의 설명이다.회전하는 [14]프레임에서 볼 수 있습니다.관측치에 대한 시간 의존적 설명은 관측치가 만들어지고 기록되는 기준 범위를 변경하지 않습니다.
국소 좌표계의 가공력

원형 [15]궤도에서 움직이는 입자에 대해 논할 때, 관성 기준 프레임에서 구심력과 접선력을 식별할 수 있다.그러면 모자를 바꾸고, 관점을 바꾸고, 일반적으로 원심력과 오일러력으로 불리는 가공의 힘에 대해 말하는 것은 문제가 되지 않는 것처럼 보인다.그러나 어휘의 이 전환의 기초가 되는 것은 우리가 시작한 관성 프레임에서 구심력과 접선력이 이치에 맞는 회전 기준 프레임으로 바뀐 것입니다. 입자가 움직이지 않고 가상의 원심력과 오일러 힘이 작용해야 하는 것입니다.그 스위치는 무의식적이지만 진짜예요
(단순한 원형 궤도가 아닌) 일반적인 평면 운동으로 입자에 앉아 있다고 가정합니다.어떤 분석이 가상의 원심력과 오일러력을 도입하기 위한 모자 전환의 기초가 되는가?
이 질문을 조사하려면 관성 기준 프레임에서 시작합니다.평면 운동에서 일반적으로 사용되는 좌표계,[16] 이른바 국소 좌표계를 사용하면, 그림 1에서와 같이 궤적에 수직인 구심 내력(그림 1에서 u와 반대 방향n)과 다음에 보이는 궤적에 평행한 접선력에 대한 공식을t 쉽게 식별할 수 있다.
그림 1에 표시된 국소 좌표계의 단위 벡터를 도입하기 위해, 한 가지 접근방식은 관성 프레임워크의 데카르트 좌표로 시작하고 이러한 데카르트 좌표를 기준으로 국소 좌표를 설명하는 것이다.그림 1에서 호 길이 s는 시간 t에서 입자가 경로를 따라 이동한 거리입니다.데카르트 좌표에 성분 x(t), y(t)가 있는 경로 r(t)는 호 길이 s(t)를 사용하여 다음과 [17]같이 설명된다.

s의 사용을 보는 한 가지 방법은 입자의 경로를 시간과 무관하게 스카이 라이터가 남긴 흔적과 같이 공간에 있다고 생각하는 것입니다.이 경로상의 모든 위치는 경로상의 어떤 시작점으로부터의 거리 s를 명시함으로써 설명됩니다.경로 ds에 따른 증분 변위는 다음과 같이 설명됩니다.
| (1) |
이 변위는 반드시 s에서 곡선에 접선하므로 곡선에 접선하는 단위 벡터는 다음과 같습니다.
이와는 별도로, 데카르트 xy 축을 따라 정렬되지 않은 단위 벡터를 사용한다고 해서 우리가 더 이상 관성 프레임에 있지 않다는 것을 의미하지는 않습니다.즉, s에 따라 다른 단위 벡터를 사용하여 경로를 설명하지만 관성 프레임에서 움직임을 관찰할 수 있습니다.
탄젠트 벡터를 사용하면 곡선에 대한 탄젠트 각도(예: θ)는 다음과 같이 지정됩니다.
s의 관점에서 경로 특성에 대한 위의 결과를 사용하여, 입자의 경로에 접선하고 정상적인 성분으로 기술된 관성 기준 프레임의 가속도는 함수 s(t) 및 다양한 시간 도함수 측면에서 찾을 수 있다(이전처럼 소수점은 s에 대한 차이를 나타낸다).
다음으로 관찰 프레임을 변경합니다.입자 위에 앉아 입자가 정지해 있는 비관성 프레임을 채택합니다(속도 0).이 프레임은 지속적으로 변화하는 원점을 가지고 있는데, 이 원점은 시간 t에 있는 경로의 곡률 중심(그림 1의 접촉 원의 중심)이며, 회전 속도는 시간 t에 있는 원점에 대한 입자의 운동 각도 속도입니다.이 비관성 프레임은 또한 궤적에 대해 수직이고 그것과 평행한 단위 벡터를 사용합니다.
이 프레임의 각 속도는 시간 t에서의 곡률 중심 주위의 입자의 각 속도입니다.관성 프레임의 구심력은 몸이 정지해 있는 비관성 프레임에서 원심력을 극복하는 데 필요한 힘으로 해석됩니다.마찬가지로, 관성 프레임에서 보이는 경로를 따라 속도의 가속을 일으키는 힘은 입자가 정지해 있는 비관성 프레임에서 오일러 힘을 극복하는 데 필요한 힘이 됩니다.프레임에는 코리올리의 힘이 없습니다.왜냐하면 이 프레임에서는 입자의 속도가 0이기 때문입니다.예를 들어, 비행기의 조종사에게 이러한 가상의 힘은 직접적인 [19]경험의 문제입니다.그러나 이러한 가공의 힘은 원과 같이 특별히 단순한 경로에 있지 않는 한 입자 자체 이외의 단순한 관측 기준 프레임과 관련될 수 없다.
즉, 정성적 관점에서 비행기의 경로는 제한된 시간 동안 원의 호로 근사할 수 있으며, 제한된 시간 동안 특정 곡률 반경이 적용되며, 원심력과 오일러 힘은 그 반경의 원형 운동을 기반으로 분석할 수 있다.비행기 선회 관련 기사를 참조하십시오.
다음으로 고정축을 중심으로 회전하는 기준 프레임에 대해 자세히 설명합니다.
극좌표에서의 가공력
입자 운동에 대한 설명은 종종 극좌표와 같은 비직교 좌표계에서 더 간단하다.운동 방정식이 곡선 좌표계의 관점에서 표현될 때, 좌표가 변화함에 따라 기저 벡터가 어떻게 변화하는지를 나타내는 추가 항이 나타납니다.이러한 항은 극좌표(또는 원통형)로 변환될 때 자동으로 발생하므로 가상의 힘이 아니라 극좌표 [20]가속에 단순히 추가된 항입니다.
두 가지 용어
순수 수학적인 처리에서는 좌표계가 연관된 프레임(관성 또는 비관성)에 관계없이 곡선 좌표를 사용할 때 관찰된 입자의 가속도에 여분의 항이 나타납니다.예를 들어 극좌표에서 가속도는 다음과 같이 표시됩니다(자세한 내용은 아래 참조).
"운동 상태"와 "좌표계"가 다른 것이 분명하다고 가정할 때, "운동 상태"에 대한 원심력의 의존성과 정확히 반대되는 의존성을 가진 "좌표계" 버전과 대조되는 "좌표계"로부터의 독립성은 두 개의 다른 아이디어가 있음을 나타낸다."부적절한 힘"이라는 용어로 지칭됩니다.본 기사에서는 이 두 가지 아이디어("운동 상태") 중 하나를 강조하지만, 다른 하나는 설명된다.
아래에서는 (첫 번째) 관성 기준 프레임에서, 그리고 (두 번째) 회전 기준 프레임에서 사용하기 위해 극좌표가 도입된다."가상력"이라는 용어의 두 가지 다른 용도가 지적된다.그러나 먼저 가상의 힘에 대한 "좌표" 용어가 어떻게 생겨났는지를 설명하기 위해 간단한 탈선을 따른다.
라그랑지안 접근법
"수학적 편의성" 이상의 참조로 "좌표" 관성력의 도입에 동기를 부여하기 위해, 다음 내용은 이러한 힘이 일부 저자들이 "일반화된" 가공력 또는 "일반화된 관성력"[24][25][26][27]이라고 부르는 것에 해당함을 보여주는 빗나감이다.이러한 힘은 일반적으로 {qk}로 표시된 일반화 좌표로 시스템을 설명하는 데 기초하는 역학에 대한 라그랑지안 역학 접근방식을 통해 도입됩니다.이들 좌표에 대한 유일한 요구사항은 시스템 상태를 고유하게 특징짓는 데 필요하고 충분하다는 것입니다. 시스템 내 입자의 좌표일 필요는 없습니다.대신, 예를 들어 로봇 팔의 링크 각도와 확장이 될 수 있습니다.기계계가 N개의 입자로 구성되어 있고 m개의 독립적인 운동학적 조건이 가해진다면, n = 3N - m의 독립적인 일반화 좌표 {qk}[28]에 의해 시스템을 고유하게 특성화할 수 있다.
고전역학에서 라그랑지안은 시스템의 운동 에너지 T T에서 잠재적 에너지 U[29]를 뺀 값으로 정의된다.기호에서는
라그랑주 역학에서 주어진 조건 하에서, 시스템의 라그랑주 방정식이 알려진 경우, 라그랑주 방정식을 오일러-라그랑주 방정식의 특정 계열인 오일러-라그랑주 방정식으로 직접 치환함으로써 시스템의 운동 방정식을 얻을 수 있다.
다음은 몇 가지 [30]정의입니다.
- 정의:라그랑주 함수 또는 라그랑주 함수i, q는 좌표, i{\({는 일반화 속도입니다.
- / L/ i ( \ \ L / \ { {_ { i } are general generalaaa 。
- § / \ \L / \ q _ { i}는 일반화 힘입니다
- d t L q i - L i 0 { \ { \ { { \ {{ _ { i } } } - { \ { { d _ { i } } } } - { \ frac { \ frac Lagrange } l l l l l l l l l l l l l l l 。
라그랑주 역학이 어떻게 작동하는지 개략적으로 설명하는 것은 여기서의 목적이 아니다.관심 있는 독자는 이 방법을 설명하는 다른 기사를 볼 수 있습니다.현재 목표는 단순히 라그랑지안 접근법이 관성 프레임에서 사라지지 않는 "일반화된 가공의 힘"을 초래할 수 있다는 것을 보여주는 것이다.여기서 관련된 것은 단일 입자의 경우, 라그랑지안 접근방식은 방금 도입된 "좌표" 가공의 힘을 정확하게 포착하도록 배열될 수 있다는 것이다.
진행하려면 하나의 입자를 고려하여 일반화k 좌표를 {q} = (r, θ)로 도입한다.그런k 다음 Hildebrand는 q = (r, θ)의 극좌표로 "일반화된 모멘타"를 보여준다.
간단히 말해서, 좌표와 그 도함수에 대한 일부 저자들의 강조와 관성 기준 프레임에서 사라지지 않는 (일반화된) 가공의 힘의 도입은 라그랑주 역학에서 일반화 좌표를 사용한 결과이다.예를 들어 McQuarrie Hildebrand [22]및 von Schwerin을 [32]참조하십시오[31].다음은 로봇 조작기 [33][34][35]설계에 사용되는 이 사용 방법의 예입니다.
위의 [Lagrange-Uler] 방정식에는 세 가지 유형의 항이 있습니다.첫 번째는 일반화 좌표의 두 번째 도함수를 포함한다.두 번째는 q 의 입니다. 여기서 계수는q\에따라 달라질 있습니다. 이들은 두 가지 유형으로 더 분류됩니다.유형 q i2의 곱을 포함하는 용어를 원심력이라고 하며, q 의 곱을 포함하는 용어를 코리올리력이라고 합니다.세 번째 유형은 q만의 함수이며 중력이라고 합니다.
--
로봇 조작기의 경우 방정식은 크리스토펠 기호 δijk(아래에서 자세히 설명)를 사용하여 다음과 [36][37]같은 형태로 작성할 수 있습니다.
일반화된 가상 힘의 도입은 종종 통지 없이 "일반화"라는 단어를 지정하지 않고 이루어집니다.이러한 허술한 용어 사용은 끝없는 혼란을 초래한다. 왜냐하면 이러한 일반화된 가공의 힘은 표준적인 "운동 상태" 가공의 힘과는 달리 관성 기준 프레임에서 사라지지 않기 때문이다.
관성 기준 프레임의 극좌표
아래에서는 극좌표를 이용하여 관성프레임에서 볼 수 있는 입자의 가속도를 도출한다.정의에 따르면 관성 프레임에는 "운동 상태" 가상 힘이 없습니다.그 프레젠테이션에 이어, 이러한 "힘"의 비벡터 변환 거동에 기초하여 "좌표" 가공 힘의 대조적인 용어를 제시하고 비판한다.
관성 프레임에서 r을를) 움직이는 입자의 위치 벡터로 .데카르트 성분(x, y)은 다음과 같습니다.
단위 벡터는 반지름 방향 로 정의됩니다
이러한 단위 벡터는 시간에 따라 방향이 달라집니다.
이러한 파생상품을 사용하여 포지션의 첫 번째 파생상품과 두 번째 파생상품은 다음과 같습니다.
그러나 수학적인 관점에서 보면 이 방정식의 오른쪽에 2차 도함수만 배치하는 것이 편리할 수 있습니다. 즉, 위의 방정식을 다음과 같이 정렬하여 작성합니다.
이 새롭게 정의된 "힘"은 관성 프레임에서 0이 아니며, 따라서 관성 프레임에서 0이고 비관성 [38]프레임에서만 0이 아닌 이전에 확인된 가공 힘과 확실히 같지 않다.이 기사에서 새로 정의된 이러한 힘은 "좌표" 원심력과 "좌표" 코리올리력으로 불리며 "운동 상태" 힘으로부터 분리됩니다.
원산지 변경
이 그림은 이른바 '중심항' 2 ( r { \ { \ } ^{2 )가 진정한 힘으로서 변환되지 않는다는 것을 보여주고 있으며, 이 용어를 단지 '항'이 아닌 원심력으로 언급하고 있습니다.프레임 S에서 입자가 원점에서 반경 방향으로 일정한 속도로 이동한다고 가정합니다.그림 2를 참조해 주세요.뉴턴의 제1법칙에 따르면 입자에 가해지는 힘은 0이다.이제 프레임 S'에서도 같은 것을 볼 수 있습니다.프레임 S'는 동일하지만 원래 위치가 바뀌었습니다.S'에서 입자는 여전히 일정한 속도로 직선 운동을 하므로 힘은 0입니다.
두 프레임에 극좌표를 사용하면 어떨까요?프레임 S에서 반경 운동은 일정하고 각도 운동은 없습니다.따라서 가속은 다음과 같습니다.
위의 사실에도 불구하고 극좌표를 채택하여 r 2{\ r}^{를 "중심력"이라고 하고 r {\을 "가속력"으로 한다고 가정합니다(가능한 정당성에 연연하지 않습니다).물리학의 적절한 공식화가 기하학이고 좌표에 의존하지 않는다는 것을 고려할 때 이 결정은 어떻게 이루어집니까?일반 공분산에 [39]대한 문서를 참조하십시오.공변식을 형성하기 위해 이 소위 원심 "힘"을 다음과 같이 벡터 표기법에 넣을 수 있습니다.
이 문제를 넘어서는 실제 가해지는 순력은 0입니다(정속에서의 직선 운동에서는 실제 가해지는 힘이 없습니다).극좌표를 채택하여 r 2{\ r}^{를 "중심력"으로 재해석하고 r 을(를) "가속력"으로 하면 프레임 S'가 됩니다. 즉, 일정한 속도에서의 직선운동에는 극좌표에서의 순력이 필요하지만 i는 필요 없습니다.n 데카르트 좌표또, 이 곤혹스러움은 프레임 S'[clarification needed]에는 해당되지만, 프레임 S에는 해당되지 않는다.
의 부조화는 r원심력이 아니라 의 두가지 용어 중 하나임을 나타낸다가속도가 두 가지 용어로 구성되어 있다는 이 관점은 프레임에 의존하지 않습니다. 즉, 모든 관성 프레임에 원심력이 0입니다.그것은 또한 좌표계에 의존하지 않는다: 우리는 데카르트, 극 또는 다른 곡선계를 사용할 수 있다: 그것들은 모두 0을 생성한다.
물론 위의 물리적 인수와는 별개로, 미분의 수학적 규칙 적용에 기초한 위의 도출은 방사 가속도가 r- 2(\{\{r}\{\theta }} 라는 두 가지 로 실제로 구성되어 있음을 보여준다.
즉, 다음 서브섹션에서는 이러한 원심력과 코리올리 항과 특정 회전 기준 프레임과 관련된 가상의 힘(관성 프레임과 구별됨) 사이에 연관성이 있음을 보여준다.
공회전 프레임
입자의 평면운동의 경우, 관성프레임에서 0이 아닌 것으로 판명된 '좌표' 원심 및 코리올리 가속항은 매우 특별한 비관성 동시회전 프레임에 나타나는 '운동상태' 원심 및 코리올리 항의 음수임을 알 수 있다(다음 [40]항 참조).그림 3을 참조해 주세요.공회전 프레임을 정의하려면 먼저 입자까지의 거리 r(t)가 정의되는 원점을 선택합니다.이 원점을 통과하는 입자의 운동면에 수직인 회전축을 설정한다.그리고 선택 모멘트 t에서 공회전 프레임 δ의 회전속도를 이 축선 dθ/dt 주위의 입자의 회전속도와 일치시킨다.공회전 프레임은 잠시 동안만 적용되며 파티클이 이동할 때 연속적으로 다시 선택해야 합니다.자세한 내용은 극좌표, 원심 및 코리올리 항을 참조하십시오.
회전 기준 프레임의 극좌표
다음으로, (비관성) 회전 프레임의 가공의 힘을 구하기 위해서 같은 어프로치를 사용한다.예를 들어 둘 다 시계 반대 방향으로 같은 속도로 회전하는 회전 극좌표계를 관측의 회전범위에서 사용하는 경우 회전범위 내의 반경 좌표는 r이지만 회전범위 내의 각도 θ'는 시간에 따라 다음과 같이 운동방정식을 구한다.
입자의 가속에서 이러한 "추가 항"은 각속도 [42]δ에서 프레임의 회전에 의해 유입되는 힘인 회전 프레임에 대한 "운동 상태" 가상 힘이다.
이 회전 프레임에서 "좌표" 가공의 힘은 무엇입니까?이전과 같이 2차 시간 도함수만 뉴턴의 법칙 오른쪽에 배치한다고 가정합니다.
편의상 {\를소위 "가속"으로 하는 경우 용어 - 2 - ) { style ( { \ \ } } ^2-{} )는 이른바 "가성 힘"에 추가되는데, 이는 "운동 상태" 가공의 힘이 아니라 실제로 δ=0일 때에도 지속되는 힘의 구성요소이다. 즉, 관성 기준 프레임에서도 지속된다.이러한 추가 항이 추가되기 때문에 "좌표" 가공력은 "운동 상태" 가공력과 동일하지 않다.이러한 추가 항 때문에 "좌표" 가공 힘은 관성 기준 프레임에서도 0이 아니다.
공동 회전 프레임에 대한 자세한 정보
단, 회전 프레임의 경우 입자와 동일한 각속도를 가지므로 특정 순간에 δ = dδ/dt(극좌표는 그림 3의 순간적인 비직접적 동일 프레임에 설정됨)가 된다.이 경우, 현시점에서는 dθdt =0 입니다.이 공회전 비관성 프레임에서 "좌표" 가상 힘은 프레임의 움직임에 의한 힘일 뿐이다. 즉, 이전 섹션의 그림 3의 공회전 프레임에 대한 비고에서 설명한 것처럼 "운동 상태" 가상 힘과 동일하다.
곡선 좌표에서의 가공력
Bullo와 Lewis를 인용하면: "예외적인 상황에서만 라그랑지안 시스템의 구성을 벡터 공간의 벡터로 설명할 수 있습니다.자연 수학 설정에서 시스템의 구성 공간은 곡면 공간, 또는 더 정확하게 미분 [43]가능한 다양체로 설명됩니다."
데카르트 좌표 대신 운동 방정식이 곡선 좌표계에서 표현될 때 크리스토펠 기호는 아래에서 자세히 설명된 바와 같이 이 좌표계에서 표현된 입자의 가속도에 나타난다.곡선 좌표에서 관성 기준 프레임의 관점에서 입자 운동에 대한 설명을 고려합니다.데카르트 좌표에서 점 P의 위치가 (x, y, z)이고 곡선 좌표에서 (q12, q3. q)라고 가정합니다.다음으로 다음 설명과 관련된 함수가 존재합니다.
이런 [48]관계를 이용해서
"운동 상태" 대 "조정" 가상 힘
앞서 이 기사에서는 두 용어 사이에 구별이 도입되었다. 이 기사에서는 관성 기준 프레임에서 사라지는 가공력을 "운동 상태" 가공력이라고 부르고 특정 좌표계의 미분에서 발생하는 가공력을 "좌표" 가공력이라고 부른다.위의 가속도에 대한 식을 사용하여 관성 기준 프레임에서 뉴턴의 운동 법칙은 다음과 같습니다.
위의 뉴턴의 법칙에 대한 "좌표" 접근법은 이 방정식의 오른쪽에 있는k 유일한 항으로서 좌표 {q}의 2차 시간 도함수를 유지하는 것이며, 물리학보다는 수학적 편의에 더 많은 동기를 부여합니다.이를 위해 힘의 법칙을 다시 작성할 수 있으며, 방정식의 힘 쪽에 대한 두 번째 합계를 다음과 같이 취할 수 있다.
프레임이 예를 들어 회전 기준 프레임에서 관성이 아닌 경우, "운동 상태" 가상 힘은 위의 "좌표" 가상 힘 [51]표현에 포함된다.또한 속도의 1차 시간 도함수로 표현된 "가속도"에 의해 단순히 시간상 좌표k {q}의 2차 도함수가 아닌 항이 발생할 경우, 2차 도함수가 아닌 항도 방정식의 힘 측에 가져와 가상의 힘에 포함된다.라그랑주 공식의 관점에서, 그것들은 일반화된 가공의 힘이라고 불릴 수 있다.예를 들어 Hildebrand를 [22]참조하십시오.
크리스토펠 기호와 가상의 힘의 "좌표" 버전에 관한 역학 공식은 운동 [35][52]방정식의 라그랑주 공식과 관련하여 로봇의 설계에 종종 사용된다.
주 및 참고 자료
- ^ 예를 들어,John Joseph Uicker; Gordon R. Pennock; Joseph Edward Shigley (2003). Theory of Machines and Mechanisms. Oxford University Press. p. 10. ISBN 0-19-515598-X., Harald Iro (2002). A Modern Approach to Classical Mechanics. World Scientific. p. Chapter 3 and Chapter 4. ISBN 981-238-213-5.
- ^ 가상 힘(의사 힘, 관성력 또는 달랑베르 힘이라고도 함)은 비관성 기준 프레임에서 관찰자를 위해 존재한다.예를 들어, NASA: Accelerated Frames of Reference를 참조하십시오. 관성력, 사이언스 조이 왜건: 원심력 - 웨이백 머신에 보관된 2018-08-04
- ^ Jerrold E. Marsden; Tudor S. Ratiu (1999). Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems. Springer. p. 251. ISBN 0-387-98643-X.
- ^ John Robert Taylor (2004). Classical Mechanics. Sausalito CA: University Science Books. p. Chapter 9, pp. 327 ff. ISBN 1-891389-22-X.
- ^ Florian Scheck (2005). Mechanics (4th ed.). Birkhäuser. p. 13. ISBN 3-540-21925-0.
- ^ Edmund Taylor Whittaker (1988). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies: With an Introduction to the Problem of Three Bodies (Fourth edition of 1936 with foreword by Sir William McCrea ed.). Cambridge University Press. p. Chapter 1, p. 1. ISBN 0-521-35883-3.
- ^ V. I. Arnol'd (1989). Mathematical Methods of Classical Mechanics. Springer. p. 129. ISBN 978-0-387-96890-2.
- ^ Harald Iroh (2002). A Modern Approach to Classical Mechanics. World Scientific. p. 180. ISBN 981-238-213-5.
- ^ Louis N. Hand; Janet D. Finch (1998). Analytical Mechanics. Cambridge University Press. p. 267. ISBN 0-521-57572-9.
- ^ K.S. Rao (2003). Classical Mechanics. Orient Longman. p. 162. ISBN 81-7371-436-3.
- ^ Jean Salençon; Stephen Lyle (2001). Handbook of Continuum Mechanics: General Concepts, Thermoelasticity. Springer. p. 9. ISBN 3-540-41443-6.
- ^ 존 D. 노튼(1993)일반 공분산과 일반 상대성 이론의 기초: 80년간의 논쟁, Prog의원. 물리, 56페이지 835-6
- ^ 관성 기준 프레임(이러한 저자들이 "뉴턴 기준 프레임"이라고 부르는 것)에서 극좌표를 다루는 무어와 스톰멜, 제2장, 페이지 26을 참조한다.
- ^ 예를 들어, Moore와 Stommel은 회전 극좌표계에서 가속도 항에는 회전 프레임의 회전 속도에 대한 참조가 포함되어 있다고 지적합니다.Henry Stommel & Dennis W. Moore (1989). An Introduction to the Coriolis Force. p. 55. ISBN 9780231066365.
- ^ 입자라는 용어는 역학에서 물체의 방향을 고려하지 않고 물체를 설명하는 데 사용됩니다.강체라는 용어는 방향 또한 하나의 요소일 때 사용됩니다.따라서 강체의 질량 중심은 "입자"이다.
- ^ 기준 및 좌표계의 관측 프레임은 독립적인 아이디어입니다.기준 프레임은 관찰자의 운동 상태와 관련된 물리적 개념입니다.좌표계는 관측치에 적합하도록 선택할 수 있는 수학적 설명입니다.시간에 따라 움직이는 좌표계의 변경은 입자 운동의 설명에 영향을 미치지만 관찰자의 운동 상태는 변경되지 않습니다.자세한 내용은 참조 범위 참조
- ^ 곡률에 관한 기사에서는 곡선이 호 길이 s가 아닌 임의의 변수(t로 표시)에 의해 매개변수화되는 보다 일반적인 경우를 다룬다.
- ^ Ahmed A. Shabana; Khaled E. Zaazaa; Hiroyuki Sugiyama (2007). Railroad Vehicle Dynamics: A Computational Approach. CRC Press. p. 91. ISBN 978-1-4200-4581-9.
- ^ 하지만 조종사는 입자가 아니기 때문에 코리올리의 힘도 경험하게 된다.예를 들어 조종사의 머리가 움직이면 머리가 비관성 프레임의 속도를 가지며 코리올리의 힘을 받게 됩니다.이 힘은 조종사의 방향 감각을 잃게 한다.Coriolis 효과(인식), 및 를 참조해 주세요.
- ^ Hugo A Jakobsen (2007). Chemical Reactor Modeling. Springer. p. 724. ISBN 978-3-540-25197-2.
- ^ Ramamurti Shankar (1994). Principles of Quantum Mechanics (2nd ed.). Springer. p. 81. ISBN 0-306-44790-8.
- ^ a b c d Francis Begnaud Hildebrand (1992). Methods of Applied Mathematics (Reprint of 2nd Edition of 1965 ed.). Courier Dover Publications. p. 156. ISBN 0-486-67002-3.
- ^ 이 문서에서는 사용되고 있지만, 이러한 이름은 일반적으로 사용되고 있지 않습니다.다른 명칭으로는 "운동 상태" 가공력 대신 "뉴턴 가공력"과 "좌표 가공력" 대신 "일반화된 가공력"이 있다.이 마지막 항은 일반화 좌표를 사용하는 역학의 라그랑지 공식에서 유래한다.참조
- ^ Donald T. Greenwood (2003). Advanced Dynamics. Cambridge University Press. p. 77. ISBN 0-521-82612-8.
- ^ Farid M. L. Amirouche (2006). Fundamentals of Multibody Dynamics: Theory and Applications. Springer. p. 207. ISBN 0-8176-4236-6.
- ^ Harold Josephs; Ronald L. Huston (2002). Dynamics of Mechanical Systems. CRC Press. p. 377. ISBN 0-8493-0593-4.
- ^ Ahmed A. Shabana (2001). Computational Dynamics. Wiley. p. 217. ISBN 0-471-37144-0.
- ^ Cornelius Lanczos (1986). The Variational Principles of Mechanics (1970 reprint of 4th ed.). Dover Publications. p. 10. ISBN 0-486-65067-7.
- ^ Cornelius Lanczos (1986). The Variational Principles of Mechanics (Reprint of 1970 4th ed.). Dover Publications. pp. 112–113. ISBN 0-486-65067-7.
- ^ Vladimir Igorevich Arnolʹd (1989). Mathematical Methods of Classical Mechanics. Springer. p. 60. ISBN 0-387-96890-3.
- ^ Donald Allan McQuarrie (2000). Statistical Mechanics. University Science Books. pp. 5–6. ISBN 1-891389-15-7.
centrifugal polar coordinates.
- ^ Reinhold von Schwerin (1999). Multibody system simulation: numerical methods, algorithms, and software. Springer. p. 24. ISBN 3-540-65662-6.
- ^ George F. Corliss, Christele Faure, Andreas Griewank, Laurent Hascoet (editors) (2002). Automatic Differentiation of Algorithms: From Simulation to Optimization. Springer. p. 131. ISBN 0-387-95305-1.
{{cite book}}:author=범용명(도움말)이 있습니다.CS1 유지: 여러 이름: 작성자 목록(링크) - ^ Jorge A. C. Ambrósio, ed. (2003). Advances in Computational Multibody Systems. Springer. p. 322. ISBN 1-4020-3392-3.
- ^ a b Shuzhi S. Ge; Tong Heng Lee; Christopher John Harris (1998). Adaptive Neural Network Control of Robotic Manipulators. World Scientific. pp. 47–48. ISBN 981-02-3452-X.
- ^ Richard M. Murray; Zexiang Li; S. Shankar Sastry (1994). A mathematical introduction to robotic manipulation. CRC Press. p. 170. ISBN 0-8493-7981-4.
- ^ Lorenzo Sciavicco; Bruno Siciliano (2000). Modelling and control of robot manipulators (2 ed.). Springer. pp. 142 ff. ISBN 1-85233-221-2.
- ^ 이 용어들을 가상의 힘으로 사용하는 치료법은 다음을 참조하십시오.
- ^ 다소 추상적이지만 완전한 설명은 를 참조하십시오.
- ^ 다음과 같은 내용 존 R테일러(2005년)를 참조하십시오.고전 역학.대학 과학 책. 우편 §9.10,를 대신하여 서명함. 358–359.아이 에스비엔 1-891389-22-X.선택한 인스턴트 t0에, 프레임 S'입자 같은 속도로...이 회전하다.그 관성에 의한 프레임에서, 힘지만 가속도 더 복잡합니다 더 단순한( 없"의제"힘) 있다.회전 프레임에, 그것은 그 반대이다
- ^ Henry Stommel & Dennis W. Moore (1989). An Introduction to the Coriolis Force. Columbia University Press. p. 55. ISBN 0-231-06636-8.
an additional centrifugal force.
- ^ 이 파생은 다음에서 찾을 수 있습니다.
- ^ Francesco Bullo; Andrew D. Lewis (2005). Geometric Control of Mechanical Systems. Springer. p. 3. ISBN 0-387-22195-6.
- ^ PM Morse & H Feshbach (1953). Methods of Mathematical Physics (First ed.). McGraw Hill. p. 25.
- ^ PM Morse & H Feshbach (1953). Methods of Mathematical Physics (First ed.). McGraw Hill. pp. 47–48.
- ^ I-Shih Liu (2002). Continuum mechanics. Springer. p. Appendix A2. ISBN 3-540-43019-9.
- ^ K. F. Riley; M. P. Hobson; S. J. Bence (2006). Mathematical Methods for Physics and Engineering. Cambridge University Press. p. 965. ISBN 0-521-86153-5.
tensor Christoffel symbol.
- ^ JL Synge & A Schild (1978). Tensor Calculus (Reprint of 1969 ed.). Courier Dover Publications. p. 52. ISBN 0-486-63612-7.
tensor Christoffel symbol.
- ^ 크리스토펠 기호 형식을 회전 좌표계에 적용하는 방법은 다음을 참조하십시오.
- ^ 두 가지 유형의 가상의 힘을 하나로 묶는 것에 대한 보다 광범위한 비판은 을 참조하십시오.
- ^ 실버스타인을 만나보세요.
- ^ 참조
추가 정보
- 프린키피아에서의 뉴턴의 기술
- 원심반력 - 콜롬비아 전자 백과사전
- M. Alonso와 E.J. Finn, 기초대학 물리학, Addison-Wesley
- 구심력 vs.원심력 - Oswego City School District의 온라인 Regents Exam 물리 튜토리얼에서 제공
- 원심력은 블랙홀 근처에서 안쪽으로 작용합니다.
- HyperPhysics 개념 현장의 원심력
- 대상 링크 목록
- Kenneth Franklin Riley; Michael Paul Hobson; Stephen John Bence (2002). "Derivatives of basis vectors and Christoffel symbols". Mathematical methods for physics and engineering: A comprehensive guide (2 ed.). Cambridge University Press. pp. 814 ff. ISBN 0-521-89067-5.
외부 링크
- 브라이언 피들러(오클라호마 대학 기상학부)의 평면 자바 물리에서의 움직임으로 가공의 힘을 나타내고 있습니다.물리릿은 회전 시점과 비회전 시점의 원근법을 모두 보여줍니다.
- 가상의 힘을 나타내는 브라이언 피들러(오클라호마 대학 기상학부)의 포물선 표면 자바 물리에서의 움직임.물리릿은 회전 시점과 비회전 시점의 원근법을 모두 보여줍니다.
- 관성 프레임과 회전 기준 프레임 모두에서 본 장면을 보여주는 애니메이션 클립으로 코리올리와 원심력을 시각화합니다.
- 산술 페이지에서 구심력과 원심력
- h2g2에서의 원심력
- 존 배즈:원심력이 달을 지탱합니까?


![{\displaystyle \mathbf {r} (s)=\left[x(s),\ y(s)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea9cb4aedaa6696cd195a0329b20a3a6d4c1f0d0)
![{\displaystyle d\mathbf {r} (s)=\left[dx(s),\ dy(s)\right]=\left[x'(s),\ y'(s)\right]ds\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f369d0a67b3fd1a430404e1948543c6cfe83d1d)
![{\displaystyle \left[x'(s)^{2}+y'(s)^{2}\right]=1\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c42e82eda34ce15d98149c930dfb7ba7cec77d)
![{\displaystyle \mathbf {u} _{t}(s)=\left[x'(s),\ y'(s)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f6a31e355c8b457ba63dc0240c2b8c5c3ecefdb)
![{\displaystyle \mathbf {u} _{n}(s)=\left[y'(s),\ -x'(s)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d6f1209c8d88eaee90a0b6cabe8eff225f320bd)







![{\displaystyle {\begin{aligned}\mathbf {a} (s)&={\frac {d}{dt}}\mathbf {v} (s)={\frac {d}{dt}}\left[{\frac {ds}{dt}}\left(x'(s),\ y'(s)\right)\right]\\&=\left({\frac {d^{2}s}{dt^{2}}}\right)\mathbf {u} _{t}(s)+\left({\frac {ds}{dt}}\right)^{2}\left(x''(s),\ y''(s)\right)\\&=\left({\frac {d^{2}s}{dt^{2}}}\right)\mathbf {u} _{t}(s)-\left({\frac {ds}{dt}}\right)^{2}{\frac {1}{\rho }}\mathbf {u} _{n}(s)\ ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf62e2af470cf7ac8350883dd103c3a3cd34c0a2)





 일반화 속도입니다.
일반화 속도입니다.





 . 여기서 계수는
. 여기서 계수는
 곱을 포함하는 용어를 원심력이라고 하며,
곱을 포함하는 용어를 원심력이라고 하며,  곱을 포함하는 용어를 코리올리력이라고 합니다.세 번째 유형은 q
곱을 포함하는 용어를 코리올리력이라고 합니다.세 번째 유형은 q
 관절 i에 대한 일반화 힘이다.따라서 크리스토펠 기호와 관련된 용어는 "일반화된 원심"과 "일반화된 코리올리" 용어를 결정합니다.
관절 i에 대한 일반화 힘이다.따라서 크리스토펠 기호와 관련된 용어는 "일반화된 원심"과 "일반화된 코리올리" 용어를 결정합니다. 
















 진정한 힘으로서 변환되지 않는다는 것을 보여주고 있으며, 이 용어를 단지 '항'이 아닌 원심력으로 언급하고 있습니다.프레임 S에서 입자가 원점에서 반경 방향으로 일정한 속도로 이동한다고 가정합니다.그림 2를 참조해 주세요.뉴턴의 제1법칙에 따르면 입자에 가해지는 힘은 0이다.이제 프레임 S'에서도 같은 것을 볼 수 있습니다.프레임 S'는 동일하지만 원래 위치가 바뀌었습니다.S'에서 입자는 여전히 일정한 속도로 직선 운동을 하므로 힘은 0입니다.
진정한 힘으로서 변환되지 않는다는 것을 보여주고 있으며, 이 용어를 단지 '항'이 아닌 원심력으로 언급하고 있습니다.프레임 S에서 입자가 원점에서 반경 방향으로 일정한 속도로 이동한다고 가정합니다.그림 2를 참조해 주세요.뉴턴의 제1법칙에 따르면 입자에 가해지는 힘은 0이다.이제 프레임 S'에서도 같은 것을 볼 수 있습니다.프레임 S'는 동일하지만 원래 위치가 바뀌었습니다.S'에서 입자는 여전히 일정한 속도로 직선 운동을 하므로 힘은 0입니다. 







 유지하면 0의
유지하면 0의  "가속력"으로
"가속력"으로 


 값이 변경되므로(그림 2 참조), 동일한 기준 프레임에 있는 관찰자는 실제 사건이 동일하더라도 서로 다른 "힘"을 볼 수 있다.l. 물리력(가짜 또는 실제)이 어떻게 한 프레임 S에서 0이 될 수 있는가? 그러나 몇 피트 떨어진 다른 프레임 S'에서는 0이 아닐 수 있는가?정확히 같은 입자 거동이라도
값이 변경되므로(그림 2 참조), 동일한 기준 프레임에 있는 관찰자는 실제 사건이 동일하더라도 서로 다른 "힘"을 볼 수 있다.l. 물리력(가짜 또는 실제)이 어떻게 한 프레임 S에서 0이 될 수 있는가? 그러나 몇 피트 떨어진 다른 프레임 S'에서는 0이 아닐 수 있는가?정확히 같은 입자 거동이라도 
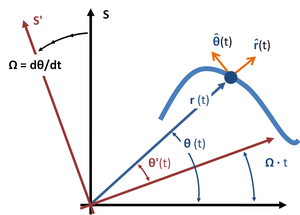


![{\displaystyle {\begin{aligned}{\frac {d^{2}\mathbf {r} }{dt^{2}}}&=\left[{\ddot {r}}-r\left({\dot {\theta }}'+\Omega \right)^{2}\right]{\hat {\mathbf {r} }}+\left[r{\ddot {\theta }}'+2{\dot {r}}\left({\dot {\theta }}'+\Omega \right)\right]{\hat {\boldsymbol {\theta }}}\\&=({\ddot {r}}-r{\dot {\theta }}'^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}'+2{\dot {r}}{\dot {\theta }}'){\hat {\boldsymbol {\theta }}}-\left(2r\Omega {\dot {\theta }}'+r\Omega ^{2}\right){\hat {\mathbf {r} }}+\left(2{\dot {r}}\Omega \right){\hat {\boldsymbol {\theta }}}\ .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04a2849482f33a30abf63f543aca1d59ac5dcc2e)


 단위 질량당 코리올리 힘의 반지름 성분입니다.
단위 질량당 코리올리 힘의 반지름 성분입니다. 


 이른바 "가성 힘"에 추가되는데, 이는 "운동 상태" 가공의 힘이 아니라 실제로 δ=0일 때에도 지속되는 힘의 구성요소이다. 즉, 관성 기준 프레임에서도 지속된다.이러한 추가 항이 추가되기 때문에 "좌표" 가공력은 "운동 상태" 가공력과 동일하지 않다.이러한 추가 항 때문에 "좌표" 가공 힘은 관성 기준 프레임에서도 0이 아니다.
이른바 "가성 힘"에 추가되는데, 이는 "운동 상태" 가공의 힘이 아니라 실제로 δ=0일 때에도 지속되는 힘의 구성요소이다. 즉, 관성 기준 프레임에서도 지속된다.이러한 추가 항이 추가되기 때문에 "좌표" 가공력은 "운동 상태" 가공력과 동일하지 않다.이러한 추가 항 때문에 "좌표" 가공 힘은 관성 기준 프레임에서도 0이 아니다.