모멘트(물리학)
Moment (physics)| 시리즈의 일부 |
| 고전 역학 |
|---|
물리학에서 모멘트는 거리와 물리량의 곱을 포함하는 수학식이다.모멘트는 일반적으로 고정된 기준점에 대해 정의되며 기준점으로부터 다소 떨어진 곳에 위치한 물리적 양을 참조합니다.이런 식으로 모멘트는 수량의 위치 또는 배치를 설명합니다.예를 들어, 종종 토크라고 불리는 힘의 모멘트는 물체에 가해지는 힘과 기준점에서 물체까지의 거리의 산물이다.원칙적으로 물리량에 거리를 곱하여 모멘트를 생성할 수 있다.일반적으로 사용되는 수량에는 힘, 질량 및 전하 분포가 포함됩니다.
정교
가장 기본적인 형태에서 모멘트는 점까지의 거리와 그 점에서의 물리량(힘이나 전하 등)의 곱입니다.
서 Q Q는 점에 가해지는 힘, 점 전하, 점 질량 등의 물리량입니다.양이 한 점에만 집중되지 않는 경우, 모멘트는 공간에 대한 해당 양의 밀도의 적분입니다.
서 { }는 전하 밀도, 질량 또는 고려되는 양의 분포입니다.
보다 복잡한 형태는 거리와 물리량 사이의 각도 관계를 고려하지만, 위의 방정식은 모멘트의 본질적인 특징, 즉 r () \ r ) or 동등한 항의 존재를 포착한다.즉, 복수의 모멘트가 존재하며(n의 값마다 1개 모멘트는 일반적으로 이 측정되는 기준점에 따라 달라지지만, 특정 모멘트(기술적으로 가장 낮은 0이 아닌 모멘트)에 대해서는 이러한 의존성이 사라지고 모멘트가 기준 poi로부터 독립된다.없습니다.
n의 각 값은 다른 모멘트에 대응합니다.첫 번째 모멘트는 n = 1에 대응하고 두 번째 모멘트는 n = 2에 대응합니다.0번째 모멘트(n = 0)는 모노폴 모멘트라고도 불리며, 첫 번째 모멘트(n = 1)는 다이폴 모멘트라고도 불리며, 두 번째 모멘트(n = 2)는 특히 전하 분포의 맥락에서 4극 모멘트라고도 불린다.
예
- 힘의 모멘트 또는 토크는 첫 번째 순간입니다. }, 더 으로r × \ \
- 마찬가지로 각운동량은 운동량의 첫 번째 모멘트이다: × \ =\ \ 운동량 자체는 모멘트가 아니다.
- 전기 쌍극자 모멘트는 첫 번째 순간이기도 합니다. 개의 반대점 전하의 경우 p d \ } 、 r ) 3 \ \mathbf 、 \r} 、 \r ( \r) ) 、 \ 、 \r 、 \ r 。
질량 모멘트:
- 총 질량은 질량의 0번째 순간이다.
- 질량 중심은 총 질량에 의해 정규화된 첫 번째 질량 이다. M i i { \ \{ 1 } { { i} \ } { r } { i } m { } _ {i ( bject mass distribution () \ ( \ )。
- 관성 모멘트는 두 번째 질량 모멘트입니다. 의경우 r 2m({ I 점 질량의 집합의 경우 })^{i}, 또는 r ( ) d 3 r \ textstyle r^2 \r ho { m( )질량의 중심은 종종 (항상 그렇지는 않지만) 참조점으로 간주됩니다
다극 모멘트
밀도 함수가 유한하고 특정 영역에 국한된다고 가정할 때, 해당 영역 밖에서 1/r 전위는 일련의 구형 고조파로 표현될 수 있다.
q m { style q _ { \ m}은 멀티폴 모멘트라고 불리며 다음과 같은 형식을 취합니다.
서 rr은 구면 좌표 、 、 {\ { \' , \right 로 표현되는 적분 변수입니다.보다 완전한 처리는 다극 팽창 또는 구형 다극 모멘트를 기술하는 페이지에서 찾을 수 있다.(주의: 위의 방정식의 표기법은 Jackson에서[1] 따온 것입니다.참조된 페이지에서 사용되는 표기법은 약간 다를 수 있습니다.
{ }가 전하 밀도를 나타내는 경우 { _ { }은 전하 모멘트의 입니다. 00 _ { m}는 단극 모멘트의 입니다. 1m { displaystyle q _ { 1 m }은 다이폴 모멘트의 입니다.({는 4극 모멘트 등을 투영한 것입니다
다극 모멘트 적용
다중극 팽창은 1/r 스칼라 전위에 적용되며, 그 예로는 전위와 중력 전위가 포함된다.이러한 전위에 대해서는, 처음 몇개의 모멘트를 계산해, 전하(또는 질량)의 국소 분포에 의해서 생성되는 장의 강도를 근사하기 위해서 이 식을 사용할 수 있다.충분히 큰 r에 대해서는 모노폴 및 다이폴 모멘트만으로 합리적인 근사치를 얻을 수 있다.고차 모멘트를 계산함으로써 높은 충실도를 달성할 수 있습니다.이 기법의 확장은 상호작용 에너지와 분자간 힘을 계산하기 위해 사용될 수 있다.
기법은 또한 알 수 없는 분포의 성질을 하기 위해 사용할 수 있다 다극 모멘트에 관한 측정치를 취하여 기초 분포의 성질을 추론하기 위해 사용할 수 있다.이 기술은 [2][3]분자와 같은 작은 물체에도 적용되지만, 우주 [4]그 자체에도 적용되어 왔다. 예를 들어 우주 마이크로파 배경 방사선을 분석하기 위해 WMAP와 플랑크 실험에서 사용된 기술이다.
역사
고대 그리스에서 유래한 것으로 여겨지는 작품에서 순간의 개념은 단어 πήrhrhrhrhrh(rhop,, "경사")와 σσππ (α(동일한 [5][6][7]경사의 이소로파)와 같은 합성물에 의해 암시된다.이 작품들의 맥락은 [8]레버와 관련된 역학과 기하학이다.특히 아르키메데스의 작품에서 이 순간은 다음과 같은 표현으로 지적된다.
- "가변 크기(δμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμμαα μα [a]μα μα μα μα μα μα μα μα μα μα α α α α α
또한, "기계 이론의 방법"과 같은 현존하는 문헌에서는 기하학적 도형의 무게 중심, 면적, 부피를 유추하기 위해 모멘트를 사용한다.
1269년, 모어베케의 윌리엄은 아르키메데스와 에우조르시의 다양한 작품들을 라틴어로 번역했다.The term ῥοπή is transliterated into ropen.[6]
1450년 경, 야코부스 크레모넨시스는 비슷한 문헌에 있는 ππή를 라틴어 모멘텀(lit.movement)[10]으로 번역했다.같은 용어는 조르지오 발라가 1501년에 번역한 후에 프란체스코 마우를리코, 페데리코 코만디노, 귀도발도 델 몬테, 아드리안 반 라멘, 플로렌스 리보, 프란체스코 부오나미키, 마린 메르센[5], 갈릴레오 갈릴레이에 의해 유지되고 있다.그런데 왜 번역에 모멘텀이라는 단어가 선택되었습니까?트레카니에 따르면 중세 이탈리아에서 초기 번역가들이 살았던 장소인 모멘토는 전달된 의미에서 "시간의 순간"과 "무게의 순간"[b]을 모두 의미한다고 한다.
1554년, 프란체스코 모를리코는 프롤로지 시브 세르몬즈라는 작품에서 라틴어의 모멘텀을 명확히 했다.다음은 Marshall Clagett이 [6]제시한 라틴어에서 영어로 번역한 것입니다.
"...등가하지 않은 거리에서의 등가중량은 동등하지 않지만, [등가하지 않은 거리에서의]등가중량은 동등할 수 있다.저울에서 알 수 있듯이 먼 거리에 매달린 중량은 더 무겁다.따라서, 특정한 세 번째 종류의 힘 또는 세 번째 크기의 차이가 존재합니다. 즉, 신체와 무게 모두와 다른 힘이며, 이것을 [c]모멘트라고 합니다.따라서, 물체는 양[즉, 크기]과 질[즉, 재료] 모두에서 무게를 획득하지만, 무게는 물체가 매달려 있는 거리로부터 모멘트를 받는다.그러므로, 거리가 무게에 반비례할 때, 아르키메데스가 "등각 [d]모멘트에 관한 책"에서 증명했듯이, 무게의 모멘트는 같다.따라서 가중치 또는 [오히려] 다른 연속량과 같은 모멘트는 공통의 종말, 즉 무게의 중심이나 평형점에서 결합됩니다.무게중심의 중심은 몸이 얼마나 자주, 또는 언제 매달려 있든 항상 우주의 중심을 향해 수직 방향으로 기울어져 있는 지점입니다.
신체, 체중, 순간 외에도, 추진력 또는 [e]힘이라고 할 수 있는 특정한 네 번째 힘이 있다.아리스토텔레스는 <기계적 질문>에서 그것을 연구했는데, 그것은 앞서 말한 세 가지[힘 또는 크기]와는 완전히 다르다.[...]"
1586년, Simon Stevin은 De Beghinselen Der Weghconst에서 기세를 나타내는 네덜란드어 staltwicht("주차 중량")을 사용했다.
1632년 갈릴레오 갈릴레이는 두 개의 주요 세계 체제에 관한 대화를 출판하고 그의 [11]전임자들 중 하나를 포함한 많은 의미를 지닌 이탈리아 모멘토를 사용한다.
1643년 토마스 살루스베리는 갈릴레이의 작품 중 일부를 영어로 번역했다.Salusbury는 라틴어 모멘텀과 이탈리아어 모멘토를 영어의 [f]모멘트로 번역합니다.
1765년, 라틴어 운동량 관성(영어: 관성 모멘트)은 호롤로지움 [12]진동에서 크리스티안 호이겐스의 수량 중 하나를 가리키기 위해 레온하르트 오일러에 의해 사용되었습니다.Huygens 1673은 1646년 Marin Mersenne에 의해 진동의 중심을 찾는 일에 자극을 받았다.[13][14]
1811년에 점과 평면에 관한 프랑스 용어 모멘트둔 힘(영어: 힘의 모멘트)은 에트리페 드 메카니크에서 [15]시메옹 드 푸아송에 의해 사용되었다.영어 번역본은 1842년에 나온다.
1884년에 James Thomson은 기계의 회전력 측정(프로펠러와 [16][17]로터 사용) 맥락에서 토크라는 용어를 제안했습니다.오늘날 동력계는 기계의 토크를 측정하기 위해 사용된다.
1893년 Karl Pearson은 곡선에 맞는 과학적 [18]측정의 맥락에서 n번째 모멘트와 스타일 _})이라는 용어를 사용했다.피어슨은 몇 년 전 기상 자료와 관련된 특이한 패턴을 관찰하고 그 원인에 [19]대한 설명을 요구한 존 벤에게 답장을 보냈다.Pearson의 응답에서는 기계적 "중력 중심"은 평균이고 "거리"는 평균으로부터의 편차라는 유추법이 사용됩니다.이것은 나중에 수학의 순간으로 진화했다.모멘트의 기계적 개념과 편차의 n제곱의 합계를 포함하는 통계 함수 사이의 유사성은 라플라스, 크램프, 가우스, 엔케, 크주버, 퀘테트, 드 [20]포레스트를 포함한 몇몇 이전 사람들에 의해 발견되었다.
「 」를 참조해 주세요.
- 토크(또는 힘의 모멘트), 기사 커플링(메트릭기)을 참조하십시오.
- 모멘트(수학)
- 역학적 평형: 피벗에 대한 시계 방향 모멘트의 합계가 동일한 피벗에 대한 시계 반대 모멘트의 합계와 같도록 물체가 균형을 이룰 때 적용됩니다.
- 관성모멘트( m 2 =\ mr는 회전운동의 논의에서 질량과 유사하다.회전 속도의 변화에 대한 물체의 저항을 나타내는 척도입니다.
- 운동량의( × mv) {{L}r} \times mathbf { ), 선형 운동량의 회전 유사체입니다
- 자기 모멘트 A } \로, 자기 소스의 강도와 방향을 측정하는 쌍극자 모멘트입니다.
- 전기 쌍극자 모멘트, 둘 이상의 전하 간 전하 차이 및 방향을 측정하는 쌍극자 모멘트.예를 들어 d의 거리로 분리된 전하 -q와 q 사이의 전기 쌍극자 모멘트는( d (\p{입니다.
- 벤딩 모멘트, 구조 요소를 벤딩하는 모멘트
- 면적의 첫 번째 모멘트, 전단 응력에 대한 저항성과 관련된 물체의 특성
- 두 번째 모멘트 면적, 휘어짐 및 휘어짐 저항과 관련된 물체의 특성
- 비틀림 저항과 관련된 물체의 특성인 극성 관성 모멘트
- 이미지 모멘트, 이미지의 통계 속성
- 지진 모멘트, 지진의 크기를 측정하는 데 사용되는 양
- 플라즈마 모멘트, 밀도, 속도 및 압력 측면에서 플라즈마의 유체 설명
- 관성 모멘트 목록
- 관성 모멘트 목록
- 다극 확장
- 구면 다극 모멘트
메모들
- ^ 또 다른 번역은 [6]1500년대에 프란체스코 마우를리코가 사용했던 "동등한 순간을 가지다"이다.문자 그대로의 번역은 "동일한 성향을 가지다"입니다.
- ^ Treccani는 moménto에 대해 다음과 같이 쓰고 있다.[... alla tradizione medievale, nella quale quotomentava, per lo pi,, minima portzion di tempo, la pi pic piccola piccola di del'ora, la pr'ora, pr'ora pr'ora prisamenta precommotamente di di del'ora (프리멘토, 1/40 di di'언 모멘토에 빌란시아 트라콜리';"
- ^ 라틴어: 모멘텀.
- ^ 이 책의 현대 번역은 "평면의 균형에 관한 것"이다.마우를리코가 사용한 "평면의 동등한 순간에" 번역은 또한 그가 아르키메데스의 생각을 고체 물체에 적용하는 De momentis aequalibus("등각적인 순간에 대하여")라는 그의 4권짜리 책에서도 메아리친다.
- ^ 라틴어: 추진력 또는 시각.이 네 번째 힘은 운동량이라고도 불리는 영국 라틴어 운동의 모멘텀의 지적 전조였다.
- ^ 이는 문서, 기념비, 논거와 같은 다른 라틴어 엔텀 단어와 매우 일치하며 프랑스어와 영어로 문서, 예를 들어 documentum, monumentum, argumentum.
레퍼런스
- ^ J. D. 잭슨, 고전 전기역학, 제2판, 뉴욕, 와일리(1975년) 페이지 137
- ^ Spackman, M. A. (1992). "Molecular electric moments from x-ray diffraction data". Chemical Reviews. 92 (8): 1769–1797. doi:10.1021/cr00016a005.
- ^ Dittrich와 Jayatilaka, 단결정 회절 데이터의 다이폴 모멘트 신뢰성 측정 및 결정 내 강화 평가, 전자 밀도 및 화학적 결합 II, 이론 전하 밀도 연구, Stalke, D(Ed), 2012, https://www.springer.com/978-3-642-30807-9.
- ^ Baumann, Daniel (2009). "TASI Lectures on Inflation". arXiv:0907.5424 [hep-th].
- ^ a b Mersenne, Marin (1634). Les Méchaniques de Galilée. Paris. pp. 7–8.
- ^ a b c d e Clagett, Marshall (1964–84). Archimedes in the Middle Ages (5 vols in 10 tomes). Madison, WI: University of Wisconsin Press, 1964; Philadelphia: American Philosophical Society, 1967–1984.
- ^ 리델, 헨리 조지, 스콧, 로버트, 페르세우스 프로젝트의 그리스 영어 어휘집
- ^ Clagett, Marshall (1959). The Science of Mechanics in the Middle Ages. Madison, WI: University of Wisconsin Press.
- ^ Dijksterhuis, E. J. (1956). Archimedes. Copenhagen: E. Munksgaard. p. 288.
- ^ "moment". Oxford English Dictionary. 1933.
- ^ Galluzzi, Paolo (1979). Momento. Studi Galileiani. Rome: Edizioni dell' Ateneo & Bizarri.
- ^ 오일러, 레온하르트(1765년).Theoria motus corporum solidorumseu rigidorum:.Exprimisnostrae cognitionis principiis stabilita(광고는 motus,huiusmodicorpora cadere possunt에 나타나기,[운동의 또는 강성 고체 상태의 물체는 이론:우리 지식은 첫번째 원칙은 해당 기관에서 발생할 수 있는 모든 동작에 적합하게 확립했습니다.](라틴어로)accommodata.로스토크와 그라이프스발트(독일):AFRöse. 페이지의 주 166. 아이 에스비엔 978-1-4297-4281-8.페이지 166:"Definitio 7.422년부터. 운동량 관성 기업은 eujuspiam 축 est otmonium productorum, quae oriuntur, si singula corpitalis elementa per quadarata distantiarum suarum ab axce multiplicentur)"(정의 7.422).어떤 축에 대한 물체의 관성 모멘트는 물체의 개별 요소에 축으로부터의 거리의 제곱을 곱할 때 발생하는 모든 곱의 합이다.)
- ^ Huygens, Christiaan (1673). Horologium oscillatorium, sive de Motu pendulorum ad horologia aptato demonstrationes geometricae (in Latin). p. 91.
- ^ Huygens, Christiaan (1977–1995). "Center of Oscillation (translation)". Translated by Mahoney, Michael S. Retrieved 22 May 2022.
- ^ Poisson, Siméon-Denis (1811). Traité de mécanique, tome premier. p. 67.
- ^ Thompson, Silvanus Phillips (1893). Dynamo-electric machinery: A Manual For Students Of Electrotechnics (4th ed.). New York, Harvard publishing co. p. 108.
- ^ Thomson, James; Larmor, Joseph (1912). Collected Papers in Physics and Engineering. University Press. p. civ.
- ^ Pearson, Karl (October 1893). "Asymmetrical Frequency Curves". Nature. 48 (1252): 615–616. doi:10.1038/048615a0. S2CID 4057772.
- ^ Venn, J. (September 1887). "The Law of Error". Nature. 36 (931): 411–412. doi:10.1038/036411c0. S2CID 4098315.
- ^ Walker, Helen M. (1929). Studies in the history of statistical method, with special reference to certain educational problems. Baltimore, Williams & Wilkins Co. p. 71.


 점에 가해지는 힘, 점 전하, 점 질량 등의 물리량입니다.양이 한 점에만 집중되지 않는 경우, 모멘트는 공간에 대한 해당 양의 밀도의
점에 가해지는 힘, 점 전하, 점 질량 등의 물리량입니다.양이 한 점에만 집중되지 않는 경우, 모멘트는 공간에 대한 해당 양의 밀도의 


 측정되는 기준점에 따라 달라지지만, 특정 모멘트(기술적으로 가장 낮은 0이 아닌 모멘트)에 대해서는 이러한 의존성이 사라지고 모멘트가 기준 poi로부터 독립된다.없습니다.
측정되는 기준점에 따라 달라지지만, 특정 모멘트(기술적으로 가장 낮은 0이 아닌 모멘트)에 대해서는 이러한 의존성이 사라지고 모멘트가 기준 poi로부터 독립된다.없습니다.











 구면 좌표
구면 좌표 표현되는 적분 변수입니다.보다 완전한 처리는
표현되는 적분 변수입니다.보다 완전한 처리는 
 전하 모멘트의
전하 모멘트의 
 4극 모멘트 등을 투영한 것입니다
4극 모멘트 등을 투영한 것입니다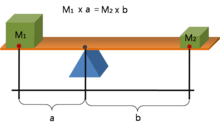
 용어를 사용했다.피어슨은 몇 년 전 기상 자료와
용어를 사용했다.피어슨은 몇 년 전 기상 자료와 




