광자

광자

광자는 외부의 청록색 레이저 빔, 내부의 주황색 레이저 빔 및 그 형광에 의해 방출됩니다.
구성.	소립자
통계학	보손의
가족	게이지 보손
상호 작용	전자기, 약한(및 중력)
기호.	γ
이론화된	알베르트 아인슈타인 (1905) "광자"라는 이름은 일반적으로 길버트 N에 기인합니다. 루이스 (1926)
덩어리	0(이론적 값) < 1x10−18 eV/c2 (실험한계)[1]
평균 수명	안정된[1]
전하	0 < 1x10e−35[1]
색전하	0
스핀	1파운드
스핀 상태	+1º, -1º
패리티	−1[1]
C 패리티	−1[1]
축약된	I(JP C)=0,1(1−−)[1]

광자(光子, )는 빛과 전파와 같은 전자기 복사와 전자기력의 전달자를 포함하는 전자기장의 양자인 기본 입자입니다.광자는 질량이 ^[a]없기 때문에 항상 진공 상태에서 빛의 속도인 299792458 m/s (또는 약 186,282 mi/s)로 움직입니다.광자는 보손 입자의 부류에 속합니다.

다른 기본 입자와 마찬가지로 광자는 양자 역학에 의해 가장 잘 설명되며 파동과 ^[2]입자의 특성을 특징으로 하는 파동-입자 이중성을 나타냅니다.현대의 광자 개념은 20세기의 첫 20년 동안 막스 플랑크의 연구를 기반으로 한 알버트 아인슈타인의 연구로 시작되었습니다.플랑크는 물질과 전자기 복사가 어떻게 서로 열평형에 있을 수 있는지 설명하려고 노력하는 동안, 물질 물체 내에 저장된 에너지는 정수의 이산적이고 동일한 크기의 부분으로 구성되어 있다고 생각해야 한다고 제안했습니다.광전 효과를 설명하기 위해, 아인슈타인은 빛 자체가 별개의 에너지 단위로 만들어진다는 생각을 소개했습니다.1926년 길버트 N. Lewis는 이러한 에너지 ^[3][4][5]단위에 대해 광자라는 용어를 대중화했습니다.그 후, 많은 다른 실험들이 아인슈타인의 ^[6][7][8]접근법을 검증했습니다.

입자 물리학의 표준 모델에서 광자와 다른 기본 입자는 시공간의 모든 점에서 특정 대칭을 갖는 물리적 법칙의 필요한 결과로 설명됩니다.전하, 질량 및 스핀과 같은 입자의 고유 특성은 게이지 대칭에 의해 결정됩니다.광자 개념은 레이저, 보스-아인슈타인 응축, 양자장 이론 및 양자 역학의 확률론적 해석을 포함한 실험 물리학과 이론 물리학에서 중대한 발전을 이끌었습니다.그것은 광화학, 고해상도 현미경 및 분자 거리 측정에 적용되었습니다.게다가, 광자는 양자 컴퓨터의 요소로서, 그리고 양자 암호화와 같은 광학 이미징 및 광학 통신의 응용을 위해 연구되어 왔습니다.

명명법

퀀타라는 단어는 1900년 이전에 전기를 포함한 다양한 양의 입자나 양을 의미하기 위해 사용되었습니다.1900년, 독일 물리학자 막스 플랑크는 흑체 복사를 연구하고 있었고, 그는 분자 내에 저장된 에너지가 "유한 등분의 ^[9]정수로 구성된 이산량"이라면 특히 더 짧은 파장에서 실험적인 관측이 설명될 것이라고 제안했습니다.1905년, 알버트 아인슈타인은 흑체 복사와 광전 효과를 포함한 많은 빛과 관련된 현상들이 공간적으로 국소화된 이산 파동 패킷으로 ^[10]구성된 전자파를 모델링함으로써 더 잘 설명될 것이라고 제안한 논문을 발표했습니다.그는 그러한 파동 패킷을 가벼운 양자(독일어: ein Lichtquant)^[b]라고 불렀습니다.

광자라는 이름은 빛을 뜻하는 그리스어인 ῶρος에서 유래했습니다.1928년 아서 콤프턴은 ^[3][11]1926년 12월 18일 네이처에 보낸 편지에서 이 용어를 만든 G.N. 루이스를 언급하며 광자를 사용했습니다.같은 이름이 이전에 사용되었지만 루이스 이전에는 결코 널리 채택되지 않았습니다: 1916년 미국 물리학자이자 심리학자인 레오나드 T. 1921년 아일랜드 물리학자 존 졸리에 의해, 1924년 프랑스 생리학자 르네 뷔름서(1890-1993)에 의해, 1926년 프랑스 물리학자 프리티프 울퍼스(1891-1971)^[5]에 의해 트롤랜드가 발견되었습니다.이 이름은 처음에 눈의 조명과 그에 따른 빛의 감각과 관련된 단위로 제안되었고 나중에 생리학적 맥락에서 사용되었습니다.비록 울퍼스와 루이스의 이론이 많은 실험에 의해 모순되었고 결코 받아들여지지 않았지만, 새로운 이름은 콤프턴이 그것을 사용한 ^[5][c]직후에 대부분의 물리학자들에 의해 채택되었습니다.

물리학에서 광자는 일반적으로 γ(그리스 문자 감마) 기호로 표시됩니다.광자에 대한 이 기호는 아마도 1903년 어니스트 러더퍼드가 이름 붙인 폴 ^[13][14]빌라드가 1900년에 발견한 감마선에서 유래했을 것이고 1914년 러더퍼드와 에드워드 안드레이드가 ^[15]전자기 복사의 한 형태로 보여주었습니다.화학과 광학 공학에서 광자는 일반적으로 광자 에너지인 hν로 표시됩니다. 여기서 h는 플랑크 상수이고 그리스 문자 γ(nu)는 광자의 ^[16]주파수입니다.

물리적 특성

광자는 질량이 ^[d]없고 ^[18][19]전하가 없으며 안정적인 입자입니다.진공 상태에서 광자는 세 가지 가능한 ^[20]편광 상태를 가집니다.광자는 ^{[21]: 29–30} 전자기학의 게이지 보손이며, 따라서 광자의 다른 모든 양자 수(렙톤 수, 중입자 수, 풍미 양자 수 등)는 ^[22]0입니다.또한 광자는 페르미-디랙 통계가 아닌 보스-아인슈타인 통계를 따릅니다.즉, 파울리 배타^{[23]: 1221} 원리를 따르지 않으며 둘 이상이 동일한 결합 양자 상태를 점유할 수 있습니다.

광자는 많은 자연적인 과정에서 방출됩니다.예를 들어, 전하가 가속되면 싱크로트론 방사선을 방출합니다.분자, 원자 또는 핵이 더 낮은 에너지 수준으로 전환되는 동안, 전파에서 감마선에 이르기까지 다양한 에너지의 광자가 방출됩니다.광자는 입자와 해당 반입자가 소멸될 때 방출될 수 있습니다(예: 전자-양전자 ^{[23]: 572, 1114, 1172} 소멸).

상대론적 에너지와 운동량

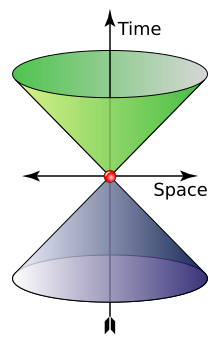
빈 공간에서 광자는 c(빛의 속도)에서 이동하고 에너지와 운동량은 E = pc에 의해 관련됩니다. 여기서 p는 운동량 벡터 p의 크기입니다.이는 m = ^[24]0인 다음과 같은 상대론적 관계에서 비롯됩니다.

${\displaystyle E^{2}=p^{2}c^{2}+m^{2}c^{4}~}$

광자의 에너지와 운동량은 오직 그 주파수(${displaystyle \nu$ 또는 반대로 파장(θ)에만 의존합니다.

${\displaystyle E=\hbar \,\omega =h\nu =sysfrac {,h\,c\,}{\delay }}$

$표시({style {boldsymbol {p}}=\hbar {boldsymbol {k}}~,}$

여기서 k는 파동 벡터, 여기서

• k k k = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion{display:sfrac-block;mw-align:-0.5em;sfrac-size:85%;text-align:center}.mwparser-outparser-outputputputputparac.mwid.n.mwd.d.d.d.d.d.d.d.mwmwd.mwarser-output .sr-only{border:0;filename:rect(0,0,0,0);높이:1px;filename:-1px;hidden;filename:0;위치:절대;폭:1px} 2px/filename은 파형입니다
• δ 2 δ는 각주파수이며,
• ħ h/2π는 감소된 플랑크 상수입니다.^[25]

p${${{$boldsymbol {p}}$가 광자의 전파 방향을 가리키기 $때문$에, 그 운동량의 크기는

${\displaystyle p\equiv \left{{\boldsymbol {p}}\right =\hbark=nu \,{c}}=displaystyle p\equiv \"left boldsymbol {p}~}$

편광 및 스핀 각운동량

광자는 또한 광자 편광과 관련된 스핀 각운동량을 전달합니다.

광자의 각운동량은 +θ 또는 -θ의 두 가지 가능한 값을 가집니다.이 두 가지 가능한 값은 원형 편광의 두 가지 가능한 순수 상태에 해당합니다.광선의 광자 집합은 이 두 값의 혼합을 가질 수 있습니다. 선형 편광 광선은 가능한 두 개의 각운동량의 동일한 수로 구성된 것처럼 작용합니다.^{[26]: 325}

빛의 스핀 각운동량은 그 주파수에 의존하지 않으며, C. V. 라만과 S에 의해 실험적으로 검증되었습니다.1931년에 ^[27]바가반탐.

반입자 소멸

자유 공간에서 반입자를 가진 입자를 소멸시키려면 다음과 같은 이유로 적어도 두 개의 광자가 생성되어야 합니다.운동량 프레임의 중심에서 충돌하는 반입자는 순 운동량이 없는 반면, 단일 광자는 항상 운동량을 가집니다(우리가 본 것처럼 광자의 주파수 또는 파장에 의해 결정되기 때문에 0이 될 수 없습니다.따라서 운동량(또는 동등하게, 번역 불변성)을 보존하려면 순 ^{[e][28]: 64–65} 운동량이 0인 광자가 적어도 두 개 생성되어야 합니다.두 광자의 에너지 또는 동등한 주파수는 4-모멘트 보존에서 결정될 수 있습니다.

다른 방법으로 볼 때, 광자는 자체 반입자로 간주될 수 있습니다(따라서 "반포톤"은 단순히 반대 운동량, 동일한 편광 및 180° 위상 이탈을 가진 일반 광자입니다).반대 과정인 쌍생성은 감마선과 같은 고에너지 광자가 ^[29]물질을 통과하는 동안 에너지를 잃는 지배적인 메커니즘입니다.그 과정은 원자핵의 전기장에서 허용되는 "하나의 광자로의 소멸"의 반대입니다.

전자기 복사의 에너지와 운동량에 대한 고전적인 공식은 광자 이벤트로 다시 표현될 수 있습니다.예를 들어, 압력은 단위 면적당 힘이고 힘은 단위 ^[30]시간당 운동량의 변화이기 때문에 물체에 대한 전자기 복사 압력은 단위 시간당 광자 운동량과 단위 면적당 광자 운동량의 전달에서 파생됩니다.

광자 질량에 대한 실험적 확인

현재 일반적으로 받아들여지는 물리적 이론은 광자가 엄격하게 질량이 없다고 암시하거나 가정합니다.광자가 엄격하게 질량이 없는 입자가 아니라면 진공 상태에서 정확한 빛의 속도 c로 움직이지 않을 것입니다.속도는 더 낮을 것이고 주파수에 따라 다릅니다.상대성 이론은 여기에 영향을 받지 않을 것입니다; 소위 빛의 속도 c는 빛이 움직이는 실제 속도가 아니라 이론적으로 어떤 물체라도 ^[31]시공간에서 도달할 수 있는 속도의 상한인 자연의 상수가 될 것입니다.따라서, 그것은 여전히 시공간의 파문(중력파와 중력자)의 속도일 것이지만, 광자의 속도는 아닐 것입니다.

만약 광자가 0이 아닌 질량을 가지고 있다면, 다른 효과들도 있을 것입니다.쿨롱의 법칙은 수정될 것이고 전자기장은 추가적인 물리적 자유도를 가질 것입니다.이러한 효과는 빛의 속도의 주파수 의존성보다 광자 질량에 대한 더 민감한 실험 프로브를 산출합니다.만약 쿨롱의 법칙이 정확하게 유효하지 않다면, 그것은 외부 전기장을 받을 때 중공 도체 내에 전기장의 존재를 허용할 것입니다.이것은 쿨롱의 ^[32]법칙에 대한 매우 고정밀 테스트를 위한 수단을 제공합니다.이러한 실험의 null 결과는 m≲ 10⁻¹⁴ eV/^[33]c의² 한계를 설정했습니다.

은하 벡터 퍼텐셜에 의한 효과를 감지하기 위해 설계된 실험에서 빛의 질량에 대한 더 날카로운 상한이 얻어졌습니다.은하 자기장이 매우 큰 길이 스케일로 존재하기 때문에 은하 벡터 퍼텐셜이 매우 크지만, 광자가 질량이 없을 경우 자기장만 관측할 수 있습니다.광자가 질량을 갖는 경우 질량 항 1/2m²AA는 은하 플라즈마에 영향을 미칠 것입니다_μ^μ.그러한 효과가 보이지 않는다는 사실은 m < 3×10⁻²⁷ eV/^[34]c의² 광자 질량에 대한 상한을 의미합니다.은하 벡터 전위는 자화된 ^[35]링에 가해지는 토크를 측정하여 직접 조사할 수도 있습니다.이러한 방법을 사용하여 입자 데이터 ^[36]그룹에서 지정한 1.07x10eV⁻²⁷/c²(10달톤 상당⁻³⁶)의 더 날카로운 상한을 얻었습니다.

은하 벡터 퍼텐셜에 의해 야기된 효과의 비관측으로 인한 이러한 급격한 한계는 모델에 ^[37]의존하는 것으로 나타났습니다.광자 질량이 힉스 메커니즘을 통해 생성되면 쿨롱의 법칙 테스트에서 m µ⁻¹⁴ 10eV/c의² 상한이 유효합니다.

역사적 발전

18세기까지의 대부분의 이론에서, 빛은 입자들로 구성되어 있는 것으로 그려졌습니다.입자 모델은 빛의 굴절, 회절, 복굴절을 쉽게 설명할 수 없기 때문에, 빛에 대한 파동 이론은 르네 데카르트 (1637),^[38] 로버트 훅 (1665),^[39] 크리스티안 하위헌스 ^[40](1678)에 의해 제안되었지만, 입자 모델은 ^[41]주로 아이작 뉴턴의 영향으로 인해 지배적으로 유지되었습니다.19세기 초, 토마스 영과 어거스트 프레넬은 빛의 간섭과 회절을 명확하게 보여주었고, 1850년까지 파동 모델이 일반적으로 ^[42]받아들여졌습니다.1888년 하인리히 헤르츠의 전파^[44] 탐지에 의해 실험적으로 확인된 빛이 전자기파라는 제임스 클러크 맥스웰의^[43] 1865년 예측은 빛의 입자 모델에 대한 마지막 타격으로 보였습니다.

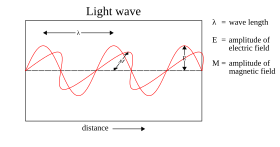
그러나 맥스웰 파동 이론이 빛의 모든 특성을 설명하는 것은 아닙니다.맥스웰 이론은 빛의 에너지가 주파수가 아닌 강도에만 의존한다고 예측합니다. 그럼에도 불구하고, 몇몇 독립적인 실험들은 빛에 의해 원자에 전달되는 에너지가 강도가 아닌 빛의 주파수에만 의존한다는 것을 보여줍니다.예를 들어, 어떤 화학 반응은 특정 임계값보다 높은 주파수의 빛에 의해서만 유발됩니다. 임계값보다 낮은 주파수의 빛은 아무리 강렬해도 반응을 시작하지 않습니다.마찬가지로, 충분히 높은 주파수의 빛을 금속판에 비추면 전자가 방출될 수 있습니다(광전 효과). 방출된 전자의 에너지는 빛의 ^[45][f]강도가 아니라 빛의 주파수에만 관련됩니다.

이와 동시에, 다양한 연구자들[47]이 40년에 걸쳐 수행한 흑체 복사에 대한 연구는 막스 플랑크의 가설[48][49]에 이르러서는 주파수 γ의 전자기 복사를 흡수하거나 방출하는 모든 시스템의 에너지는 에너지 양자 E = hν의 정수배라는 것에 도달했다,[10][50] 어떤 형태의 en에너지 양자화는 물질과 전자기 복사 사이에서 관찰된 열 평형을 설명하기 위해 가정되어야 합니다; 광전 효과에 대한 이러한 설명으로, 아인슈타인은 1921년 노벨 ^[51]물리학상을 받았습니다.

빛의 맥스웰 이론은 전자기 복사의 가능한 모든 에너지를 허용하기 때문에, 대부분의 물리학자들은 처음에 에너지 양자화가 복사를 흡수하거나 방출하는 물질에 대한 알려지지 않은 제약에서 비롯되었다고 가정했습니다.1905년, 아인슈타인은 에너지 양자화가 전자기 복사 그 ^[10]자체의 특성이라고 처음으로 제안했습니다.비록 그는 맥스웰 이론의 타당성을 받아들였지만, 아인슈타인은 맥스웰 광파의 에너지가 ^[10]공간에 지속적으로 전파되더라도 서로 독립적으로 움직이는 점과 같은 양자로 국소화된다면 많은 변칙적인 실험이 설명될 수 있다고 지적했습니다.1909년과^{[50] [52]}1916년에 아인슈타인은 만약 흑체 복사에 관한 플랑크의 법칙이 받아들여진다면, 에너지 양자는 운동량 p = h / µ를 전달해야 하며, 이는 완전한 입자가 된다는 것을 보여주었습니다.이 광자 운동량은 아서 ^[53]콤프턴에 의해 실험적으로 관찰되었고, 1927년 노벨상을 수상했습니다.그렇다면 가장 중요한 질문은 맥스웰의 빛에 대한 파동 이론을 실험적으로 관찰된 입자 특성과 어떻게 통합하느냐 하는 것이었습니다.이 질문에 대한 답은 알버트 아인슈타인의 남은 ^[54]삶을 차지했고, 양자 전기역학과 그 후계자인 표준 모델에서 해결되었습니다.(아래의 ① 양자장 이론과 ② 게이지 보손으로서 참조)

아인슈타인의 1905년 예측은 로버트 밀리칸의 노벨상 ^[55]강연에서 설명한 것처럼 20세기의 첫 20년 동안 여러 가지 방법으로 실험적으로 검증되었습니다.하지만, 콤프턴의 실험이^[53] 광자가 그들의 파동수 ^{[full citation needed]}(1922)에 비례하는 운동량을 전달한다는 것을 보여주기 전에, 대부분의 물리학자들은 전자기 복사 자체가 미립자일 수 있다는 것을 믿기를 꺼렸습니다.(예를 들어 빈,^[47] 플랑크^[49], 밀리칸의 노벨상 강연 참조).^[55]대신, 에너지 양자화는 방사선을 흡수하거나 방출하는 물질에 대한 알려지지 않은 제약에서 비롯된다는 믿음이 널리 퍼져 있었습니다.태도는 시간이 지남에 따라 변했습니다.부분적으로, 그 변화는 관측된 ^[56]결과를 설명하기 위해 빛 자체에 양자화를 설명하지 않는 것이 훨씬 더 어려웠던 콤프턴 산란을 밝히는 것과 같은 실험으로 추적될 수 있습니다.

콤프턴의 실험 이후에도 닐스 보어, 헨드릭 크레이머스, 존 슬레이터는 빛의 맥스웰 연속 전자기장 모델, 이른바 BKS ^[57]이론을 보존하기 위해 마지막 시도를 했습니다.BKS 이론의 중요한 특징은 에너지 보존과 운동량 보존을 어떻게 처리했는지입니다.BKS 이론에서, 에너지와 운동량은 물질과 방사선 사이의 많은 상호 작용에서 평균적으로만 보존됩니다.그러나 정제된 콤프턴 실험은 보존 법칙이 개별 ^[58]상호 작용에 대해 유효하다는 것을 보여주었습니다.따라서, 보어와 그의 동료들은 그들의 ^[54]모델에게 "가능한 한 명예로운 장례식"을 주었습니다.그럼에도 불구하고, BKS 모델의 실패는 베르너 하이젠베르크의 매트릭스 ^[59]역학 개발에 영감을 주었습니다.

몇몇 물리학자들은^[60] 전자기 복사가 양자화되지 않지만 물질이 양자 역학의 법칙을 따르는 것처럼 보이는 반고전적 모델을 개발하는 것을 고집했습니다.비록 1970년대에 광자의 존재에 대한 화학적, 물리적 실험의 증거가 압도적이었지만, 이 증거는 절대적으로 확정적으로 여겨질 수 없었습니다. 왜냐하면 그것은 빛과 물질의 상호 작용에 의존했고, 충분히 완전한 물질 이론은 원칙적으로 증거를 설명할 수 있기 때문입니다.그럼에도 불구하고, 모든 반고전 이론은 1970년대와 1980년대에 광자 상관 ^[g]실험에 의해 결정적으로 반박되었습니다.따라서 양자화는 빛의 속성 그 자체라는 아인슈타인의 가설은 증명된 것으로 간주됩니다.

파동-입자 이중성 및 불확실성 원리

광자는 양자역학의 법칙을 따르기 때문에, 그들의 행동은 파동적인 측면과 입자적인 측면을 모두 가지고 있습니다.측정 기기에서 광자를 감지하면 단일 입자 단위로 등록됩니다.그러나 광자를 검출할 확률은 파동을 설명하는 방정식에 의해 계산됩니다.이러한 측면의 조합을 파동-입자 이중성이라고 합니다.예를 들어, 광자가 감지될 수 있는 위치에 대한 확률 분포는 회절 및 간섭과 같은 파동과 같은 현상을 명확하게 표시합니다.이중 슬릿을 통과하는 단일 광자는 맥스웰의 파동 ^[63]방정식에 의해 결정된 간섭 패턴에 의해 주어진 확률 분포로 화면의 한 지점에서 에너지를 수신합니다.하지만, 실험은 광자가 전자기 방사선의 짧은 펄스가 아님을 확인합니다. 광자의 맥스웰 파동은 회절되지만 광자 에너지는 전파하면서 확산되지 않으며 빔 스플리터를 만날 ^[64]때 이 에너지가 분할되지 않습니다.오히려, 수신된 광자는 원자핵과 같은 파장보다 훨씬⁻¹⁵ 작은 시스템이나 심지어 점과 같은 전자를 포함한 임의의 작은 시스템에 의해 전체적으로 흡수되거나 방출되기 때문에 점과 같은 입자처럼 작용합니다.

많은 입문서가 비상대론적 양자 역학의 수학적 기술을 사용하여 광자를 다루는 반면, 광자는 본질적으로 상대론적이기 때문에 이것은 어떤 면에서 어색한 과도한 단순화입니다.광자는 정지 질량이 0이기 때문에 광자에 대해 정의된 파동 함수는 비상대론적 양자 ^[h]역학의 파동 함수에서 익숙한 모든 특성을 가질 수 없습니다.이러한 어려움을 피하기 위해 물리학자들은 아래에 설명된 광자의 두 번째 양자화 이론인 광자가 전자기 모드의 여기를 양자화하는 ^[69]양자 전기 역학을 사용합니다.

또 다른 어려움은 불확실성 원리에 대한 적절한 아날로그를 찾는 것입니다. 하이젠베르크는 전자와 고에너지 광자를 포함하는 사고 실험을 분석할 때 이 개념을 도입했습니다.하지만, 하이젠베르크는 이러한 측정에서 "불확실성"이 무엇을 의미하는지에 대한 정확한 수학적 정의를 제공하지 않았습니다.위치-운동량 불확실성 원리의 정확한 수학적 진술은 케나드, 파울리, 바일에 ^[70][71]기인합니다.불확실성 원리는 실험자가 입자의 위치와 운동량과 같이 두 개의 "공역적인" 양 중 하나를 측정할 수 있는 상황에 적용됩니다.불확도 원리에 따르면 입자가 어떻게 준비되든 위치 측정 결과가 더 확실해지면 운동량 측정 결과가 더 작아지고 그 ^[72]반대의 경우도 마찬가지라는 두 가지 대체 측정 결과에 대해 정확한 예측을 할 수 없습니다.일관된 상태는 양자 역학이 ^[69]허용하는 한 전체적인 불확실성을 최소화합니다.양자 광학은 전자기장 모드에 일관된 상태를 사용합니다.전자파의 진폭 측정과 위상 사이에는 위치-운동량 불확실성 ^[69]관계를 연상시키는 트레이드오프가 있습니다.이것은 때때로 전자파에 존재하는 광자 수의 불확실성인 $(디스플레이$ 스타일 $\Delta$ N$)$과 파동 위상의 불확실성인 $({디스플레이$ 스타일 $\Delta \phi$로 비공식적으로 표현됩니다. 하지만 이것은 케너드-폴리-의 불확실성 관계일 수 없습니다.위치 및 운동량과 달리 위상$$δ({$displaystyle \phi})$는 에르미트 ^[73]연산자로 나타낼 수 없습니다.

광자 가스의 보스-아인슈타인 모델

1924년 사티엔드라 나스 보스는 전자기학을 사용하지 않고 위상 ^[74]공간의 거친 입자 계수를 수정하여 플랑크의 흑체 복사 법칙을 도출했습니다.아인슈타인은 이 수정이 광자가 엄격하게 동일하다고 가정하는 것과 같고 대칭 양자 역학 상태의 요구 사항으로 이해되는 "신비한 비국소적 상호 작용"^[75][76]을 암시한다는 것을 보여주었습니다.이 작업은 일관성 있는 상태의 개념과 레이저의 개발로 이어졌습니다.같은 논문에서 아인슈타인은 보스의 형식주의를 물질 입자(보손)로 확장하고 충분한 온도에서 가장 낮은 양자 상태로 응축될 것이라고 예측했습니다;^[77] 이 보스-아인슈타인 응축은 1995년에 실험적으로 관찰되었습니다.그것은 나중에 Lene Hau에 의해 1999년과 ^[79]2001년에^[78] 빛을 느리게 하고 완전히 멈추기 위해 사용되었습니다.

이것에 대한 현대적인 관점은 광자가 정수 스핀으로 인해 (반 정수 스핀을 가진 페르미온과 반대로) 보손이라는 것입니다.스핀 통계 정리에 따르면, 모든 보손은 보스-아인슈타인 통계를 따릅니다(모든 페르미온은 페르미-디랙 ^[80]통계를 따릅니다).

자극 및 자발적 방출

1916년, 알버트 아인슈타인은 플랑크의 방사선 법칙이 광자와 원자의 반고전적이고 통계적인 처리로부터 파생될 수 있다는 것을 보여주었고, 이는 원자가 광자를 방출하고 흡수하는 속도 사이의 연관성을 암시합니다.이 조건은 원자에 의한 방사선의 방출과 흡수의 기능이 서로 독립적이며, 열평형이 방사선과 원자의 상호작용을 통해 만들어진다는 가정에서 비롯됩니다.열평형의 공동이 그 자체의 모든 부분과 전자기 복사로 채워져 있고 원자가 그 복사를 방출하고 흡수할 수 있다고 생각해보세요.열평형은 진동수가 θ(θ)인 광자의 에너지 밀도가 평균적으로 일정해야 하며, 따라서 광자가 방출되는 속도는 흡수되는 속도와 같아야 한다.[81]

아인슈타인은 관련된 다양한 반응 속도에 대한 간단한 비례 관계를 가정하기 시작했습니다.그의 모형에서, 시스템이 낮은 에너지 Ej에서 높은 에너지 Ei로 전환하여 낮은 에너지 Ej의 광자를 흡수하는 속도 Rji({displaystyle R_{ji})는 에너지 Ej({displaystyle E_{j})를 가진 원자의 NJ({displaystyle N_{j})와 에너지 D(displaystyle)에 비례한다그$$ 주파수의 주변 광자에 대한 $민감$도${\displaystyle \rho }$ (${\displaystyle }$ν$$) {\$displaystyle \rho (\nu)},$

${\displaystyle R_{ji}=N_{j}B_{ji}\rho(\nu)\!}$

$여기$서 $({$는 흡수율 상수입니다.역 과정의 경우, 두 가지 가능성이 있습니다: 광자의 자발적 방출 또는 원자와 지나가는 광자의 상호 작용 및 원자의 낮은 에너지 상태로의 복귀에 의해 시작된 광자의 방출.아인슈타인의 접근법에 따르면, 주파수$\delta {\displaystyle }$({$displaystyle R_{$ij$$$})$의 광자 방출과$$더 높은 $에너지{\displaystyle {}_{}}$ ${\displaystyle {Ei}_{}}$({$displaystyle E_{i})$에서 더 낮은 $에너지{\displaystyle {}_{}}$ $({$로의 전환에 대한 해당 ${\displaystyle {\mathrm{속도}}_{}}$는 다음과 같습니다.

${\displaystyle R_{ij}=N_{i}A_{ij}+N_{i}B_{ij}\rho (\nu )\!}$

$여기$서 $({$는 광자를 자발적으로 방출하는 속도 상수이고, $({$는 주변 광자(유도 방출 또는 자극 방출)에 대한 반응에 대한 속도 상수입니다.열역학적 평형 상태에서, $상태$가 i${displaystyle$ i$$$}$인 원자와 $상태$가$$j{$displaystyle$ j$}$인 원자의 수는 평균적으로 일정해야 하므로, $({$ji})와$$ $({$의 $비율$은 같아야 합니다.또한, 볼츠만 통계의 파생과 유사한 주장에 따르면, Ni({displaystyle N_{i})와 Nj({j})의 비율은 gi / gj exp ⁡ (Ej - Ei ) / (k T ), \displaystyle g_{i}/g_{j}\exp {(E_{j}-E})이며, 여기서 gsty_{j}는 gsty}의 상태를 나타낸다$Lei}$와 j${displaystyle$$j$$\}$의 각각$Ei{$${\displaystyle {displaystyle}_{}}$ E_{i$}$와 Ej${$displaystyle E_${j}$의 에너지, 볼츠만 상수$$$k{\displaystyle }$ 및 T${displaystyle$ T$}$의 시스템 온도.$이$로부터, ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {\mathrm{Bij}}_{}}$ $=$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {\mathrm{Bji}}_{}}${$displaystyle g_{i}B_{ij$}=$g_{j}B_{ji}$와

${\displaystyle A_{ij}=displayfrac {8\pih\nu ^{3}}{c^{3}}B_{ij}}$

$({$와 $({$는 총칭하여 아인슈타인 ^[82]계수로 알려져 있습니다.

아인슈타인은 자신의 속도 방정식을 완전히 정당화할 수는 없었지만, 물리학자들이 "양자 가설에 맞게 수정된 역학과 전기역학"을 얻으면 계수 Aij, Bij를 계산할 수 있어야 한다고 주장했다.[83]얼마 지나지 않아 1926년 폴 디랙은 반고전적 ^[84]접근법을 사용하여 Bij$($ ${\displaystyle {\mathrm{스타일}}_{}}$ $B_{ij})$ $속도$ 상수를 도출했고, 1927년에는 양자 ^[85][86]이론의 틀 안에서 첫 번째 원리로부터 모든 속도 상수를 도출하는 데 성공했습니다.디랙의 연구는 양자전기역학, 즉 전자기장 자체의 양자화의 기초였습니다.Dirac의 접근법은 두 번째 양자화 또는 양자장 ^[87][88][89]이론이라고도 불립니다; 초기의 양자 역학적 처리는 물질 입자를 전자기장이 아닌 양자 역학으로만 취급합니다.

아인슈타인은 자발적으로 방출된 광자의 방향을 결정하지 않았기 때문에 그의 이론이 불완전해 보인다는 사실에 고민했습니다.빛 입자 운동의 확률론적 특성은 뉴턴이 복굴절과 더 일반적으로 인터페이스에서 빛 빔을 투과 빔과 반사 빔으로 분할하는 처리에서 처음 고려되었습니다.뉴턴은 빛 입자의 숨겨진 변수가 단일 광자가 취할 ^[41]두 경로 중 어떤 경로를 결정한다는 가설을 세웠습니다.유사하게, 아인슈타인은 양자역학과의 분리를^[54] 시작하면서, 운에 아무것도 남기지 않는 더 완전한 이론을 희망했습니다.역설적이게도, 파동^[90][91] 함수에 대한 맥스 보른의 확률론적 해석은 더 완전한 ^[92]이론을 찾는 아인슈타인의 후기 연구에서 영감을 받았습니다.

양자장론

전자기장의 양자화

1910년, 피터 데비는 플랑크의 흑체 복사 법칙을 비교적 간단한 ^[93]가정에서 도출했습니다.그는 공동의 전자기장을 푸리에 모드로 분해했고, 어떤 모드에서든 에너지가 ${\displaystyle h}$의 $정수$ 배수라고 가정했습니다. 여기서$γ$${\displaystyle$$\nu}$는 전자기 모드의 주파수입니다.플랑크의 흑체 복사 법칙은 기하학적 합으로 바로 이어집니다.하지만,^[50] 데비의 접근법은 1909년 아인슈타인에 의해 도출된 흑체 복사의 에너지 변동에 대한 정확한 공식을 제공하지 못했습니다.

1925년, Born, Heisenberg, Jordan은 데비의 개념을 핵심적인 ^[94]방법으로 재해석했습니다.고전적으로 보여질 수 있는 것처럼, 전자기장의 푸리에 모드(파 벡터 k와 편광 상태에 의해 색인화된 전자기 평면파의 완전한 집합)는 결합되지 않은 단순 고조파 발진기의 집합과 같습니다.양자 역학적으로 처리된 이러한 발진기의 에너지 수준은 E$=$ ${\displaystyle \mathrm{nh}}$$\nu {\displaystyle }$ {\$displaystyle$$$E = $nh\nu$이며, 여기서$$ν {\$displaystyle$ \$nnu}$는 발진기 주파수입니다.핵심적인 새로운 단계는 $에너지{\displaystyle }$ E$=$ ${\displaystyle \mathrm{nh}}$${\displaystyle \nu }$ {{$displaystyle$ E$=$$nh$\nu$}$를 각각의 $에너지{\displaystyle }$ h$$ν ${{$$displaystyle$n$\}$개의$$ 광자를 $가진{\displaystyle }$ 상태로 식별하는 것이었습니다. 이 접근 방식은 올바른 에너지 변동 공식을 제공합니다.

디랙은 이것을 한 걸음 ^[85][86]더 나아갔습니다.그는 전하와 전자기장 사이의 상호 작용을 전체적으로 에너지와 운동량을 보존하면서 광자 상태의 전환을 유도하는 작은 섭동으로 취급했습니다.디랙은 $아인슈타인$의 $Aij$$계수$와$Bij$계수를$$ 첫 번째 원리에서 도출할 수 있었습니다$.$광자의 보스-아인슈타인 통계는 전자기장을 정확하게 양자화한 자연스러운 결과임을 보여주었습니다(보스의 추론은 반대 방향으로 진행되었습니다; 그는 B-E 통계를 가정하여 플랑크의 흑체 복사 법칙을 도출했습니다).디랙의 시대에, 광자를 포함한 모든 보손이 보스-아인슈타인 통계를 따라야 한다는 것은 아직 알려지지 않았습니다.

디랙의 2차 섭동 이론은 가상 광자, 전자기장의 과도적 중간 상태를 포함할 수 있습니다. 정적 전기 및 자기 상호 작용은 이러한 가상 광자에 의해 매개됩니다.이러한 양자장 이론에서 관측 가능한 사건의 확률 진폭은 물리적이지 않은 모든 가능한 중간 단계를 합산하여 계산된다. 따라서 가상 광자는 E = pc{displaystyle E=pc}를 만족하도록 제한되지 않으며 추가 편광 상태를 가질 수 있다실제 광자의 두 가지 상태 대신에 3-4개의 편광 상태를 유지합니다.이러한 일시적인 가상 광자는 결코 관찰될 수 없지만, 관측 가능한 ^[95]사건의 확률에 측정 가능하게 기여합니다.실제로, 그러한 2차 및 고차 섭동 계산은 총합에 명백하게 무한한 기여를 할 수 있습니다.이러한 비물리적 결과는 ^[96]재규격화 기법을 사용하여 수정됩니다.

다른 가상 입자도 합에 기여할 수 있습니다. 예를 들어, 두 광자는 가상 전자-양전자 ^[97]쌍을 통해 간접적으로 상호 작용할 수 있습니다.전자-광자 산란뿐만 아니라 이러한 광자-광자 산란(2광자 물리학 참조)은 계획된 입자 가속기인 국제 선형 ^[98]충돌기의 작동 모드 중 하나입니다.

현대 물리학 표기법에서 전자기장의 양자 상태는 각 전자기 모드에 대한 상태의 텐서 곱인 포크 상태로 기록됩니다.

${\displaystyle n_{k_{0}}\rangle \otimes n_{k_{1}}\rangle \otimes \otimes n_{k_{n}}\rangle \times }$

여기서 n k ⟩ \ displaystyle n_{k_{i}\rangle은 n k \ displaystyle \,n_{k_{i}}개의 광자가 모드 k k \ displaystyle k_{i}에 있는 상태를 나타낸다. 이 표기법에서 모드 k k에서 새로운 광자의 생성(예: 원자 전이에서 방출)은 nk → k + displaystydisplaystyle {k}로 기술된다$ngle \rightarrow n_{k_{i}}+1\rangle$ 이 표기법은 위에서 설명한 Born, Heisenberg 및 Jordan의 개념을 나타낼 뿐 물리학을 추가하지 않습니다.

게이지 보손으로

전자기장은 게이지 필드로 이해될 수 있습니다. 즉,^[99] 게이지 대칭이 시공간의 모든 위치에서 독립적으로 유지되어야 하는 결과로 발생하는 필드입니다.전자기장의 경우, 이 게이지 대칭은 절대값 1의 복소수의 아벨 U(1) 대칭이며, 이는 관측 가능한 값이나 에너지 또는 라그랑지안과 같은 실제 값 함수에 영향을 주지 않고 복소수 필드의 위상을 변화시키는 능력을 반영합니다.

아벨 게이지 필드의 양자는 대칭이 깨지지 않는 한 무질량 전하 입자여야 합니다. 따라서 광자는 무질량이고 전하 및 정수 스핀을 가질 것으로 예측됩니다.전자기 상호 작용의 특정 형태는 광자가 ±1 회전을 가져야 한다고 지정합니다. 따라서 광자의 헬리시티는 $ℏ{{$displaystyle $\pm \hbar$이어야 합니다. 이 두 스핀 구성 요소는 오른손과 왼손 원형 편광의 고전적인 개념에 해당합니다.그러나 양자 전기 역학의 일시적 가상 광자는 비물리적 편광 ^[99]상태를 채택할 수도 있습니다.

일반적인 물리학 표준 모델에서 광자는 전약 상호 작용에서 4개의 게이지 보손 중 하나이며, 나머지 3개는 W, W⁻, Z로⁰ 표시되며⁺ 약한 상호 작용을 담당합니다.광자와 달리, 이 게이지 보손은 SU(2) 게이지 대칭을 깨는 메커니즘으로 인해 질량이 있습니다.전약 상호작용에서 W 및 Z 게이지 보손과 광자의 통일은 셸던 글래쇼, 압두스 살람, 스티븐 와인버그에 의해 달성되었으며 1979년 노벨 ^{[100][101][102]}물리학상을 수상했습니다.물리학자들은 이 네 개의 게이지 보손과 양자 색역학의 여덟 개의 글루온 게이지 보손을 연결하는 대규모 통합 이론을 계속 가설하고 있습니다. 하지만 양성자 붕괴와 같은 이러한 이론의 핵심 예측은 ^[103]실험적으로 관찰되지 않았습니다.

강입자 성질

에너지 광자와 강입자 사이의 상호 작용 측정은 강입자의 전하와 광자의 상호 작용에 의해 예상되는 것보다 상호 작용이 훨씬 더 강렬하다는 것을 보여줍니다.게다가, 양성자와 중성자의 전하 구조가 상당히 다르지만, 에너지 광자와 양성자의 상호 작용은 광자와^[104] 중성자의 상호 작용과 유사합니다.이 효과를 설명하기 위해 벡터 중간자 지배라고 불리는 이론이 개발되었습니다.VMD에 따르면 광자는 전하 및 벡터 ^[105]중간자와만 상호 작용하는 순수 전자기 광자의 중첩입니다.그러나 매우 짧은 거리에서 실험적으로 조사되면 광자의 본질적인 구조는 쿼크와 글루온 성분의 플럭스로 인식되고 QCD의 점근 자유에 따라 준자유이며 광자 구조 ^[106][107]함수에 의해 설명됩니다.2000년 리뷰에서 이론적 예측과 데이터의 포괄적인 ^[108]비교가 제시되었습니다.

시스템 질량에 대한 기여

광자를 방출하는 시스템의 에너지는 방출 시스템의 나머지 프레임에서 측정된 광자의 에너지 E(디스플레이 스타일 E)에 의해 감소하며, 이는 E/c2({displaystyle {E}/{c^{2}})의 질량 감소를 초래할 수 있다. 마찬가지로 광자를 흡수하는 시스템의 질량은 상응하는 양만큼 증가한다.응용 프로그램으로, 광자와 관련된 핵 반응의 에너지 균형은 일반적으로 관련된 핵의 질량과 감마 광자(그리고 ^[109]핵의 반동 에너지와 같은 다른 관련 에너지에 대한 E${$ $형식$의 용어로 작성됩니다.

이 개념은 양자 전기 역학의 주요 예측에 적용됩니다(QED, 위 참조).그 이론에서, 전자의 질량(또는 더 일반적으로, 렙톤)은 재정규화라고 알려진 기술에서 가상 광자의 광자의 질량 기여를 포함함으로써 수정됩니다.이러한 "방사선 보정"은 렙톤의 자기 쌍극자 모멘트, 램 시프트, 뮤오늄 ^[110]및 포지트로늄과 같은 결합된 렙톤 쌍의 초미세 구조와 같은 QED의 많은 예측에 기여합니다.

일반 상대성 이론에 따르면 광자는 응력-에너지 텐서에 기여하기 때문에 다른 물체에 중력을 작용시킵니다.반대로, 광자는 중력에 의해 영향을 받습니다. 보통 직선 궤도는 중력 렌즈에서와 같이 뒤틀린 시공간에 의해 구부러질 수 있고, 파운드-렙카 실험에서와 같이 더 높은 중력 전위로 이동함으로써 주파수가 낮아질 수 있습니다.그러나 이러한 효과는 광자에만 국한되지 않습니다. 고전적인 ^[111]전자파에 대해서도 정확히 동일한 효과가 예측될 수 있습니다.

물질적으로

투명한 물질을 통과하는 빛은 진공에서 빛의 속도인 c보다 낮은 속도로 이동합니다.속도가 감소하는 요인을 재료의 굴절률이라고 합니다.고전적인 파동 그림에서, 속도가 느려지는 것은 물질에서 전기 편광을 유도하는 빛, 새로운 빛을 방출하는 편광 물질, 그리고 새로운 빛이 원래의 빛의 파동을 방해하여 지연된 파동을 형성하는 것으로 설명될 수 있습니다.입자 사진에서, 속도 저하는 대신 광자와 물질의 양자 들뜸의 혼합으로 설명되어 편광자로 알려진 준입자(다른 준입자는 이 목록 참조)를 생성할 수 있습니다. 이 편광자는 유효 질량이 0이 아니므로 c에서 이동할 수 없습니다.서로 다른 주파수의 빛은 다른 속도로 물질을 통과할 수 있습니다. 이를 분산(산란과 혼동하지 않음)이라고 합니다.어떤 경우에, 그것은 물질에서 빛의 속도를 극도로 느리게 만들 수 있습니다.다른 준입자와의 광자 상호작용의 영향은 라만 산란과 브릴루인 ^[112]산란에서 직접 관찰될 수 있습니다.

광자는 물질에 의해 산란될 수 있습니다.예를 들어, 광자는 태양의 중심부에서 오는 길에 너무 많은 충돌을 일으켜 복사 에너지가 ^[113]표면에 도달하는 데 약 백만 년이 걸릴 수 있습니다; 하지만, 일단 열린 공간에 들어가면, 광자는 ^[114]지구에 도착하는 데 8.3분밖에 걸리지 않습니다.

광자는 또한 핵, 원자 또는 분자에 의해 흡수될 수 있으며, 에너지 수준 사이의 전환을 유발합니다.전형적인 예는 1958년 노벨상 수상자 생화학자 조지 발드와 동료들에 의해 발견된 시각에 책임이 있는 레티날(CHO₂₀₂₈)의 분자 전이입니다.흡수는 시스-트랜스 이성질화를 유발하며, 이는 다른 전이와 결합하여 신경 임펄스로 전달됩니다.광자의 흡수는 염소의 광분해에서와 같이 화학적 결합을 깨뜨릴 수도 있습니다. 이것은 ^[115][116]광화학의 주제입니다.

기술 응용 프로그램

광자는 기술에서 많은 응용 분야를 가지고 있습니다.이러한 예는 고전적인 빛 이론에서 작동할 수 있는 렌즈 등과 같은 일반적인 광학 장치가 아닌 광자 자체의 적용을 설명하기 위해 선택됩니다.레이저는 매우 중요한 응용 분야이며 위에서 자극 방출 하에서 논의됩니다.

개별 광자는 몇 가지 방법으로 감지할 수 있습니다.고전적인 광전자 증배관은 광전 효과를 이용합니다. 충분한 에너지의 광자가 금속판에 부딪혀 전자를 자유롭게 하여 전자의 눈사태를 더욱 증폭시킵니다.반도체 전하 결합 장치 칩은 유사한 효과를 사용합니다. 입사 광자는 감지할 수 있는 미세 커패시터에 전하를 생성합니다.가이거 계수기와 같은 다른 검출기는 광자의 능력을 사용하여 장치에 포함된 가스 분자를 이온화하여 ^[117]가스의 감지 가능한 전도도 변화를 유발합니다.

플랑크의 에너지 $공식{\displaystyle }$ E$=$ ${\displaystyle h}$ {\$displaystyle$ E=$h\nu}$는 광자 흡수로 인한 에너지 변화를 계산하고 주어진 광자 방출에서 방출되는 빛의 주파수를 결정하기 위해 설계 엔지니어와 화학자에 의해 종종 사용됩니다.예를 들어, 가스 방전 램프의 방출 스펙트럼은 서로 다른 전자 에너지 수준 ^[118]구성을 가진 (혼합물) 가스로 채워서 변경할 수 있습니다.

어떤 조건에서는 에너지 전이가 개별적으로 불충분한 "두 개의" 광자에 의해 들뜨게 될 수 있습니다.이는 샘플이 서로 다른 색상의 두 빔이 크게 겹치는 스펙트럼에서만 에너지를 흡수하기 때문에 고해상도 현미경을 사용할 수 있습니다(2광자 여기 현미경 참조).게다가, 이 광자들은 더 ^[119]낮은 에너지를 가지고 있기 때문에 샘플에 더 적은 피해를 줍니다.

어떤 경우에는 두 개의 에너지 전환이 결합되어 한 시스템이 광자를 흡수할 때 다른 가까운 시스템이 에너지를 "도둑질"하고 다른 주파수의 광자를 재방출할 수 있습니다.이것은 분자생물학에서 적절한 ^[120]단백질의 상호작용을 연구하기 위해 사용되는 기술인 형광 공명 에너지 전달의 기초입니다.

몇 가지 다른 종류의 하드웨어 난수 생성기는 단일 광자의 검출을 포함합니다.하나의 예에서, 생성될 무작위 시퀀스의 각 비트에 대해, 광자는 빔 분할기로 전송됩니다.이러한 상황에서 동일한 확률의 두 가지 가능한 결과가 있습니다.실제 결과는 시퀀스의 다음 비트가 "0"인지 "1"^[121][122]인지 확인하는 데 사용됩니다.

양자 광학과 계산

양자 광학 분야에서 광자의 응용에 많은 연구가 할애되어 왔습니다.광자는 매우 빠른 양자 컴퓨터의 요소로 적합한 것으로 보이며, 광자의 양자 얽힘은 연구의 초점입니다.비선형 광학 프로세스는 2광자 흡수, 자기 위상 변조, 변조 불안정성 및 광학 파라메트릭 발진기와 같은 주제를 가진 또 다른 활발한 연구 영역입니다.그러나 이러한 프로세스는 일반적으로 광자 자체를 가정할 필요가 없습니다. 종종 원자를 비선형 진동자로 취급하여 모델링할 수 있습니다.자발적 매개 변수 다운 변환의 비선형 과정은 종종 단일 광자 상태를 생성하는 데 사용됩니다.마지막으로, 광자는 광학 통신의 일부 측면, 특히 양자 ^[123]암호화에 필수적입니다.

2광자 물리학은 광자 사이의 드문 상호작용을 연구합니다.2018년, MIT 연구원들은 편광자를 ^[124][125]포함할 수 있는 결합된 광자 세쌍둥이의 발견을 발표했습니다.

참고 항목

메모들

레퍼런스

진일보한 내용

외부 링크

• Wiki Quote에서 광자와 관련된 인용문
• Wiktionary에서 광자의 사전적 정의
• Wikimedia Commons의 포토와 관련된 미디어