양자수
Quantum number| 에 관한 일련의 기사의 일부 |
| 양자역학 |
|---|
양자 물리학과 화학에서 양자 수는 양자 시스템의 역학에서 보존된 양의 값을 나타냅니다.양자 번호는 해밀턴과 함께 이동하는 연산자의 고유값(시스템 에너지와 동시에[note 1] 정밀하게 알 수 있는 양)과 그에 상응하는 고유값에 해당합니다.양자계의 모든 양자수의 사양은 시스템의 기본상태를 완전히 특징지어 원칙적으로 함께 측정할 수 있다.
양자역학의 중요한 측면은 많은 관측 가능한 [note 2]관심량의 양자화이다.특히, 이것은 양자수가 이산적인 정수 집합이나 반정수 집합의 값을 취하도록 유도한다. 그러나 경우에 따라서는 무한대에 근접할 수 있다.이것은 질량, 전하 또는 운동량과 같은 시스템을 특징짓는 모든 값이 연속적으로 분포하는 고전 역학과 양자 역학을 구별합니다.양자수는 종종 원자에 있는 전자의 에너지 수준을 구체적으로 설명하지만, 다른 가능성에는 각운동량, 스핀 등이 포함됩니다.중요한 계열은 풍미 양자수입니다. 즉, 입자의 유형과 기본 힘을 통해 입자와 다른 입자의 상호작용을 결정하는 내부 양자수입니다.어떤 양자계도 하나 이상의 양자수를 가질 수 있다. 따라서 모든 가능한 양자수를 나열하는 것은 어렵다.
주어진 시스템에 필요한 양자수
양자수의 집계는 시스템마다 다르며 보편적인 해답은 없다.따라서 분석할 각 시스템에 대해 이러한 파라미터를 찾아야 합니다.양자화된 시스템은 적어도 하나의 양자수를 필요로 한다.양자 시스템의 역학(즉, 시간 진화)은 양자 연산자에 의해 해밀턴 H의 형태로 설명된다.시스템의 에너지에 해당하는 시스템의 양자 수는 하나, 즉 해밀턴의 고유값 중 하나입니다.각 선형 독립 연산자 O에 대해 해밀턴과 통신하는 하나의 양자 번호가 있습니다.해밀턴호와 함께 통근하는 완전한 통근 관측 장치(CSCO)는 모든 양자 번호로 시스템을 특징짓습니다.양자 번호와 CSCO 연산자 사이에는 일대일 관계가 있으며, 각 양자 번호는 해당 연산자의 고유값 중 하나를 취합니다.통근 오퍼레이터의 완전한 세트를 형성하기 위해서 임의로 선택될 수 있는 다른 베이스의 결과로서, 다른 상황에서의 동일 시스템의 기술에는 다른 세트의 양자수를 사용할 수 있다.
원자 중의 전자
4개의 양자수가 원자의 전자를 완전히 설명할 수 있습니다.
그러나 스핀-궤도 상호작용은 이러한 숫자와 관련이 있다.따라서, 이러한 기저 벡터에 대해 직교 선택이 이루어진 경우, 더 적은 양자 수로 시스템에 대한 완전한 설명을 제공할 수 있습니다.
특이성
시스템의 다른 전자는 다른 양자수를 가질 것이다.예를 들어 점유율이 가장 높은 궤도 전자, 실제 분화 전자(즉, 원소를 앞의 것과 구별하는 전자), aufbau 근사치에 따른 분화 전자.랜턴에서는, 한층 더 예를 들면, 관련하는 전자는 각각 6s, 5d, 4f 오비탈에 있다.이 경우 주요 양자 수는 6, 5, 4입니다.
공통 용어
여기서 사용되는 모델은 아래에 주어진 네 개의 양자수 n, θ, mℓ, m을s 사용하여 전자를 기술합니다.또한 핵입자 상태(예: 양성자와 중성자)의 고전적 설명에서 일반적인 명명법이다.분자 궤도에 대한 양자 설명은 해밀턴과 그 대칭이 다르기 때문에 다른 양자 수를 필요로 한다.
주양자수
주요 양자수는 전자의 전자껍질, 즉 에너지 수준을 나타냅니다.n의 값은 1부터 원자의 가장 바깥 전자를 포함하는 껍질까지이다[1].
- n = 1, 2, ...
예를 들어 세슘(Cs)에서 가장 바깥쪽에 있는 원자가 전자는 에너지 레벨이 6인 셸에 있으므로 세슘의 전자는 1에서 6까지의 n 값을 가질 수 있습니다.
시간 독립 퍼텐셜에 있는 입자의 경우(슈뢰딩거 방정식 참조), 각 운동량(J를2 포함하는 항)에 의한 기여로 에너지 E의 n번째 고유값도 표시합니다.따라서 이 숫자는 전자와 핵 사이의 거리(즉, 반경 좌표 r)에만 의존합니다.평균 거리는 n만큼 증가합니다.따라서 서로 다른 주요 양자수를 갖는 양자 상태는 서로 다른 껍질에 속한다고 한다.
방위 양자수
방위 양자수(각운동량 양자수 또는 궤도 양자수)는 부껍질을 설명하고 관계를 통해 궤도 각운동량의 크기를 나타냅니다.
- L2 = ħ2 ( ( + 1 + 1)
화학 및 분광학에서 θ = 0은 s 오비탈, θ = 1, p 오비탈, θ = 2, d 오비탈, θ = 3, f 오비탈이라고 한다.
δ 값은 0 ~ n - 1이므로 첫 번째 p 궤도(θ = 1)는 두 번째 전자 껍질(n = 2)에 나타나고 첫 번째 d 궤도(θ = 2)는 세 번째 껍질(n = 3)에 나타나는 식이다.[2]
- θ = 0, 1, 2, ... - 1
n = 3,420 = 0으로 시작하는 양자수는 원자의 세 번째 전자껍질의 s 오비탈에 있는 전자를 나타낸다.화학에서, 이 양자수는 매우 중요하다. 왜냐하면 그것은 원자 궤도의 모양을 지정하고 화학 결합과 결합 각도에 강한 영향을 미치기 때문이다.방위 양자수는 또한 궤도에 존재하는 각도 노드의 수를 나타낼 수 있다.예를 들어 p 오비탈의 경우 θ = 1이므로 p 오비탈의 각도 노드 양은 1이다.
궤도의 모양은 방위 양자수로도 주어진다.
자기 양자수
자기 양자 번호는 해당 하위 껍질 내의 특정 궤도(또는 "구름")를 나타내며 지정된 축을 따라 궤도 각 운동량을 투영합니다.
- Lz = mℓ µ
mℓ 값은 정수 간격으로 [3][page needed]-4 ~0 입니다.
s 부껍질(s subshell)은 하나의 궤도만을 포함하므로, s 오비탈에서 전자의 m은ℓ 항상 0이 될 것이다.p 하위껍질(p 하위껍질 = 1)은 세 개의 궤도(일부 시스템에서는 세 개의 "소형" 구름으로 표시됨)를 포함하므로, p 오비탈에서 전자의 m은ℓ -1, 0 또는 1이 됩니다.d 하위 쉘(표준 = 2)에는 -2, -1, 0, 1, 및 2의 m 값을 가진ℓ 5개의 궤도가 포함됩니다.
스핀 양자수
스핀 양자 수는 각 궤도 내에서 전자의 고유 스핀 각 운동량을 나타내며 지정된 축을 따라 스핀 각 운동량 S의 투영을 제공합니다.
- Sz = ms µ.
일반적으로 m 값은s -s에서 s까지이며, 여기서 s는 입자의 고유 스핀 각 [4]운동량과 관련된 스핀 양자수이다.
- ms = -s, -s + 1, -s + 2, ..., s - 2, s - 1, s.
전자){수 s.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den spin다.Border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/2, 결과적으로)±1/2 것이다,"스핀 업 하다"과"스핀 다운하다"국가들을 가리킨다.파울리 배타 원리로 인해 개별 궤도에 있는 각 전자는 서로 다른 양자 수를 가져야 하며, 따라서 궤도는 절대 두 개 이상의 전자를 포함하지 않습니다.
규칙.
m과s m에는 범용ℓ 고정값이 없습니다.오히려ℓ m과s m 값은 임의입니다.선택에 이 상수의 유일한 제약 조건은 이 명명 schematic 계산 또는 설명의 특별한 집합 안에 사용했다(예를 들어, 궤도 첫 전자로 궤도에 종사하mℓ)−1 또는 mℓ)0또는mℓ=1로 묘사될 수는 있지만 다음 짝 안지은 전자의 궤도의mℓ 값 b.야 한다 일치해야만 한다는 것이다ed그러나 다른 궤도의 전자에 할당된 m은ℓ 다시 m = -1 또는ℓ m = 0 또는ℓ m = 1)일ℓ 수 있다.
이러한 규칙은 다음과 같이 요약됩니다.
이름. 기호. 의미. 값의 범위 가치의 예 주양자수 n 껍데기 1 µn n = 1, 2, 3, … 방위 양자수(각운동량) ℓ 서브셸(오비탈은 0, p 오비탈은 1 등) 0 ≤ℓ n - 1 n = 3의 경우:
θ = 0, 1, 2 (s, p, d)자기 양자수(각운동량 투영) 마ℓ 궤도(오비탈 방향) - m mℓ 。 = 2의 경우:
mℓ = -2, -1, 0, 1, 2스핀 양자수 마s 전자의 스핀(-1/2 = "스핀 다운", 1/2 = "스핀 업") - s ms m ≤ s 전자 s = 1/2일 경우,
따라서s m = -1/2, +1/2
예제:2p 원자 궤도에 위치한 탄소(C) 원자의 가장 바깥쪽 원자가 전자에 사용되는 양자수는 n = 2 (2번째 전자껍질), δ = 1 (p 오비탈 부껍질ℓ), m = 1, 0, -1, ms = 1/2 (전자 스핀)이다.
분광학 결과에 따르면 최대 두 개의 전자가 하나의 궤도를 차지할 수 있습니다.그러나 파울리 배타 원리를 다루는 훈드의 규칙에 따르면 두 전자는 절대 같은 정확한 양자 상태나 같은 양자 수의 집합을 가질 수 없다.두 개의 가능한 값으로 스핀을 나타내는 네 번째 양자수는 충돌을 해결하기 위한 임시 가정으로 추가되었다. 이 가정은 나중에 상대론적 양자 역학과 유명한 스턴-게라크 실험의 결과에 의해 자세히 설명될 것이다.
배경
양자역학의 역사를 통해 많은 다른 모델들이 제안되었지만, 가장 두드러진 명명 체계는 Friedrich Hund, Robert S.의 Hund-Mulliken 분자 궤도 이론에서 비롯되었습니다. 뮬리켄, 그리고 슈뢰딩거, 슬레이터, 존 레너드 존스의 공헌.이 명명 체계는 보어 에너지 수준, 훈드-뮬리켄 궤도 이론, 그리고 분광학과 훈드의 법칙에 [5]기초한 전자 스핀에 대한 관찰을 통합했습니다.
총 각도 모멘타 수
입자의 총 각운동량
스핀-오빗 상호작용을 고려할 때 L 연산자와 S 연산자는 더 이상 해밀턴 연산자와 함께 이동하지 않으므로 고유값은 시간이 지남에 따라 변한다.따라서 다른 양자수 집합을 사용해야 합니다.이 세트에는[6][7] 다음이 포함됩니다.
예를 들어 양자 번호로 정의되는 다음 8가지 상태를 생각해 보겠습니다.
n ℓ 마ℓ 마s § + s § - s mℓ + ms (1) 2 1 1 +1/2 3/2 1/23/2 (2) 2 1 1 - 1/2 3/2 1/2 1/2 (3) 2 1 0 +1/2 3/2 1/2 1/2 (4) 2 1 0 - 1/2 3/2 1/2 - 1/2 (5) 2 1 −1 +1/2 3/2 1/2 - 1/2 (6) 2 1 −1 - 1/2 3/2 1/2- 3/2 (7) 2 0 0 +1/2 1/2 - 1/2 1/2 (8) 2 0 0 - 1/2 1/2 - 1/2 - 1/2
시스템의 양자 상태는 이러한 8개 상태의 선형 조합으로 설명할 수 있습니다.그러나 스핀-오빗 상호작용이 존재하는 경우, 해밀턴의 고유 벡터인 8개의 상태로 동일한 시스템을 기술하려면(즉, 각각이 시간에 따라 다른 것과 섞이지 않는 상태를 나타냄), 다음 8개의 상태를 고려해야 한다.
j 마j 패리티 3/2 3/2 이상한 상기 (1)상태에서 오는 모습 3/2 1/2 이상한 상기 (2) 및 (3)상태에서 오는 3/2 - 1/2 이상한 상기 (4) 및 (5)의 주로부터 오는 3/2 - 3/2 이상한 위 (6)상태에서 오는 1/2 1/2 이상한 상기 (2) 및 (3)상태에서 오는 1/2 - 1/2 이상한 상기 (4) 및 (5)의 주로부터 오는 1/2 1/2 심지어. 상기의 상태(7)에서 오는 모습 1/2 - 1/2 심지어. 위 (8)상태에서 오는 모습
핵각운동량 양자수
핵에서, 양성자와 중성자의 전체 집합(핵자)은 각 핵자의 각 모멘타(일반적으로 I로 표기)로 인해 결과적으로 각 운동량을 가진다.중성자의 총 각운동량이 j = δ + s이고n 양성자의 경우 j = δ + s(양성자와 중성자의 경우 s가 다시 1/2(주 참조))이면p 핵 각운동량 양자수는 다음과 같이 주어진다.
- I = jn - jp , jn - jp + 1, jn - jp + 2, ..., (jn + jp) - 2, (jn + jp) - 1, (jn + jp)
참고: 핵(및 원자) 상태의 궤도 각 모멘타는 모두 θ의 정수 배수이며, 중성자와 양성자의 고유 각 모멘텀은 반정수 배수이다.핵자의 고유 스핀과 궤도 운동을 조합하면 홀수 A 핵의 총 스핀 I에 대한 반정수 값, 짝수 A 핵에 대한 정수 값이 항상 제공된다는 것은 즉시 명백해질 것이다.
핵 각운동량 상태 표기에 사용되는 수치 I와의 동등성은 수소(H), 탄소(C), 나트륨(Na)의 일부 동위원소의 예는 다음과 같다.[8]
1
1HI = (1/+2) 9
6C
.I = (3/−2) 20
11나I = 2+ 2
1HI = 1+ 10
6C
.I = 0+ 21
11나I = (3/+2) 3
1HI = (1/+2) 11
6C
.I = (3/−2) 22
11나I = 3+ 12
6C
.I = 0+ 23
11나I = (3/+2) 13
6C
.I = (1/−2) 24
11나I = 4+ 14
6C
.I = 0+ 25
11나I = (5/+2) 15
6C
.I = (1/+2) 26
11나I = 3+
단 하나의 핵자의 차이에도 불구하고, I의 비정상적인 변동의 이유는 양성자와 중성자의 홀수 및 짝수 때문이다 – 핵자 쌍은 홀수 또는 짝수인 핵자를 남기는 총 각운동량이 0이다.핵 스핀의 특성은 외부 자기장과 상호작용하는 핵자기 모멘트로 인해 유기 [7]화학에서는 NMR 분광학, [8]핵의학에서는 MRI의 운영에 중요한 요소이다.
소립자
소립자는 보통 소립자에 고유하다고 하는 많은 양자수를 포함하고 있다.그러나 소립자는 입자 물리학의 표준 모델의 양자 상태이며, 따라서 이러한 입자의 양자 수는 Bohr 원자의 양자 수가 Hamiltonian에 미치는 것과 같은 관계를 가지고 있다는 것을 이해해야 한다.즉, 각 양자수는 문제의 대칭을 나타냅니다.양자장 이론에서는 시공간 대칭과 내부 대칭을 구별하는 것이 더 유용하다.
시공간 대칭과 관련된 대표적인 양자수는 스핀(회전 대칭과 관련), 패리티, C 패리티 및 T 패리티(시공간 Poincaré 대칭과 관련)입니다.대표적인 내부 대칭은[clarification needed] 렙톤수, 바리온수 또는 전하입니다.(이런 종류의 양자수의 전체 목록은 풍미에 관한 기사를 참조하십시오.)
곱셈 양자수
대부분의 보존된 양자수는 가법적이기 때문에 소립자 반응에서 양자수의 합은 반응 전과 후에 같아야 한다.그러나 일반적으로 패리티라고 불리는 일부는 곱셈입니다. 즉, 그 곱은 보존됩니다.모든 곱셈 양자수는 대칭(패리티와 같은 것)에 속하며 대칭 변환을 두 번 적용하는 것은 아무것도 하지 않는 것과 같습니다(혁신).
「 」를 참조해 주세요.
메모들
레퍼런스
- ^ Beiser, A. (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1.[페이지 필요]
- ^ Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. Vol. 1. Oxford University Press. ISBN 0-19-855129-0.[페이지 필요]
- ^ Eisberg & Resnick 1985.
- ^ Peleg, Y.; Pnini, R.; Zaarur, E.; Hecht, E. (2010). Quantum Mechanics. Schuam's Outlines (2nd ed.). McGraw Hill (USA). ISBN 978-0-07-162358-2.[페이지 필요]
- ^ 화학, 물질, 우주, R.E. Dickerson, I. Geis, W.A. Benjamin Inc., 1976, ISBN 0-19-855148-7
- ^ Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. Vol. 1. Oxford University Press. ISBN 0-19-855129-0.[페이지 필요]
- ^ a b Atkins, P. W. (1977). Molecular Quantum Mechanics Part III: An Introduction to Quantum Chemistry. Vol. 2. Oxford University Press.[ISBN 실종][페이지 필요]
- ^ a b Krane, K. S. (1988). Introductory Nuclear Physics. John Wiley & Sons. ISBN 978-0-471-80553-3.[페이지 필요]
추가 정보
- Dirac, Paul A. M. (1982). Principles of quantum mechanics. Oxford University Press. ISBN 0-19-852011-5.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Halzen, Francis & Martin, Alan D. (1984). QUARKS AND LEPTONS: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2.
- Eisberg, Robert Martin; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. ISBN 978-0-471-87373-0 – via Internet Archive.
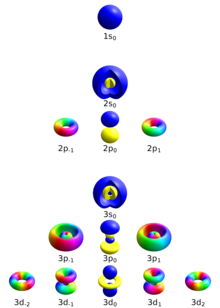

 (는) 동시에 대각선화가 가능하므로
(는) 동시에 대각선화가 가능하므로 


