Page semi-protected

중력

Gravity
기타 용도는 중력(동음이의하지 않음)을 참조하십시오.
"중력"과 "중력의 법칙"은 여기로 방향을 바꿉니다. 기타 용도는 중력(동음이의) 및 중력 법칙(동음이의)을 참조하십시오.
사진 속 두 개의 거대한 은하의 모양은 중력으로 인해 왜곡되어 있습니다.
에 관한 시리즈의 일부
고전역학
운동 제2법칙
나뭇가지
기본사항
제형
핵심 주제
로테이션
사이언티스트

물리학에서 중력은 질량을 가진 모든 물체 사이에 상호 인력을 일으키는 근본적인 상호 작용입니다.[1] 중력은 네 가지 기본 상호작용 중 단연코 가장 약한 것으로 강한 상호작용보다 약 10배38, 전자기력보다 10배36, 약한 상호작용보다 10배나29 약합니다. 그 결과 아원자 입자 수준에서는 큰 영향을 미치지 않습니다.[2] 그러나 중력은 거시적 규모에서 물체 사이의 가장 중요한 상호작용이며, 행성, 별, 은하, 심지어 빛의 움직임을 결정합니다.

지구에서는 중력이 물리적인 물체에 무게를 주고, 달의 중력은 바다의 달 아래 조수를 담당합니다. (대항행 조수는 지구와 달이 서로 궤도를 도는 관성에 의해 발생합니다.) 중력은 또한 많은 중요한 생물학적 기능을 가지고 있어, 중력의 과정을 통해 식물의 성장을 안내하고 다세포 생물의 유체 순환에 영향을 미칩니다.

우주의 원래 기체 물질 사이의 중력의 인력으로 인해 결합하여 별을 형성하고 결국 은하계로 응축되었기 때문에 중력은 우주의 많은 대규모 구조물을 담당합니다. 중력은 무한한 범위를 가지고 있지만, 물체가 멀어질수록 그 효과는 약해집니다.

중력은 일반상대성이론(Albert Einstein, 1915년 제안)에 의해 가장 정확하게 설명되는데, 중력을 힘이 아니라 시공간의 곡률로 설명하는데, 이는 질량의 불균등한 분포로 인해 발생하고, 질량이 측지선을 따라 이동하게 하기 때문입니다. 이 시공간 곡률의 가장 극단적인 예는 블랙홀인데, 블랙홀의 사건 지평선을 지나면 빛조차 빠져나올 수 없는 것이 없습니다.[3] 그러나 대부분의 응용 분야에서 중력은 뉴턴의 만유인력 법칙에 의해 잘 근사화되며, 중력은 질량의 곱에 비례하고 그들 사이의 거리의 제곱에 반비례합니다.

입자물리학의 현재 모델은 아마도 양자중력, 초중력 또는 중력 특이점의 형태로, 일반적인 공간과 시간과 함께 플랑크 시대(우주 탄생 후 최대 10초−43) 동안에 개발되었으며, 아마도 원시 상태에서 시작되었을 것이라는 것을 암시합니다. 현재 알려지지 않은 방식으로 거짓 진공, 양자 진공 또는 가상 입자와 같은.[4] 과학자들은 현재 양자역학과 일치하는 중력 이론을 개발하기 위해 노력하고 있습니다.[5] 양자 중력 이론은 중력이 물리학의 다른 세 가지 근본적인 상호 작용과 공통의 수학적 틀(모든 것에 대한 이론)에서 통합되도록 허용합니다.

정의들

중력은 우주의 모든 질량들 사이의 상호적인 인력입니다. 중력은 행성이나 다른 천체의 표면에 있는 중력의 인력입니다.[6] "중력"은 중력 외에도 행성의 회전에 따른 원심력을 포함할 수 있습니다(#지구 중력 참조).[7]

역사

주요 기사: 중력 이론의 역사

고대세계

중력의 본질과 메커니즘은 다양한 고대 학자들에 의해 탐구되었습니다. 그리스에서 아리스토텔레스는 지구가 우주의 중심이고 우주의 모든 질량을 지구 쪽으로 끌어당기기 때문에 물체가 지구 쪽으로 떨어진다고 믿었습니다. 그는 또한 떨어지는 물체의 속도가 무게와 함께 증가해야 한다고 생각했는데, 이는 나중에 거짓으로 밝혀진 결론이었습니다.[8] 아리스토텔레스의 견해는 고대 그리스 전역에서 널리 받아들여졌지만, 중력의 인력이 지구에만 있는 것이 아니라고 정확히 예측한 플루타르코스와 같은 다른 사상가들도 있었습니다.[9]

중력을 힘으로 이해하지는 못했지만, 고대 그리스 철학자 아르키메데스는 삼각형의 무게 중심을 발견했습니다.[10] 그는 또한 같은 무게의 두 개가 같은 무게중심을 가지고 있지 않다면, 두 무게의 무게중심은 그들의 무게중심을 잇는 선의 가운데에 있을 것이라고 가정했습니다.[11] 2세기 후, 로마의 공학자이자 건축가인 비트루비우스는 그의 De Architectura에서 중력은 물질의 무게가 아니라 물질의 "성질"에 의존한다고 주장했습니다.[12] 서기 6세기 비잔티움 알렉산드리아 학자 존 필로포누스(John Philoponus)는 시간이 지남에 따라 감소하는 원인력을 통합하여 "운동의 지속은 힘의 지속적인 작용에 달려 있다"는 아리스토텔레스의 이론을 수정한 추진력 이론을 제안했습니다.[13]

서기 7세기에 인도의 수학자이자 천문학자인 브라마굽타는 중력이 물체를 지구로 끌어당기는 매력적인 힘이라는 아이디어를 제안했고 그것을 묘사하기 위해 구루트바카르 ṣ ṇ라는 용어를 사용했습니다.

고대 중동에서 중력은 치열한 논쟁의 주제였습니다. 페르시아의 지식인 알비루니는 중력의 힘이 지구만의 것이 아니라고 믿었고, 그는 다른 천체들도 중력의 인력을 발휘해야 한다고 정확하게 가정했습니다.[17] 이에 비해 알카지니는 우주의 모든 물질이 지구의 중심에 끌린다는 아리스토텔레스와 같은 입장을 견지했습니다.[18]

기울어진 피사의 탑 전설에 따르면 갈릴레오가 낙하하는 물체의 속도에 대한 실험을 수행했습니다.

과학혁명

주요 기사: 과학혁명

16세기 중반, 다양한 유럽 과학자들은 무거운 물체가 더 빠른 속도로 떨어진다는 아리스토텔레스적인 개념을 실험적으로 반증했습니다.[19] 특히 스페인 도미니카 신부 도밍고 데 소토(Domingo de Soto)는 1551년 자유낙하 상태의 신체가 균일하게 가속한다고 썼습니다.[19] 데 소토는 신체의 타락에 대한 아리스토텔레스의 가르침과 모순되는 베네데토 바르치, 프란체스코 베토, 루카 기니, 그리고 지오반 벨라소를 포함하여, 이탈리아의 다른 도미니카 사제들에 의해 시행된 초기의 실험들에 의해 영향을 받았을 수 있습니다.[19] 16세기 중반 이탈리아의 물리학자 지암바티스타 베네데티는 비중 때문에 같은 물질로 만들어졌지만 질량이 다른 물체는 같은 속도로 떨어질 것이라고 주장하는 논문을 발표했습니다.[20] 플랑드르의 물리학자 사이먼 스테빈은 1586년 델프트 타워 실험을 통해 타워에서 떨어질 때 크기와 무게가 다른 두 개의 대포알이 같은 속도로 떨어지는 것을 관찰했습니다.[21] 마침내 16세기 후반 갈릴레오 갈릴레이가 구르는 공들을 자세히 측정한 결과, 중력 가속도는 모든 물체에 동일하다는 사실을 확실히 확인할 수 있었습니다.[22] 갈릴레오는 공기 저항이 밀도가 낮고 표면적이 높은 물체가 대기에서 더 느리게 떨어지는 이유라고 가정했습니다.

1604년 갈릴레오는 낙하하는 물체의 거리가 경과한 시간의 제곱에 비례한다는 가설을 정확하게 세웠습니다.[23] 이것은 나중에 1640년에서 1650년 사이에 이탈리아의 과학자인 예수회 그리말디와 리치올리에 의해 확인되었습니다. 그들은 또한 진자의 진동을 측정함으로써 지구 중력의 크기를 계산했습니다.[24]

뉴턴의 중력 이론

주요 기사: 뉴턴의 만유인력 법칙과 역제곱 법칙에 대한 뉴턴-후크 우선순위 논쟁

1657년, 로버트 훅은 그의 현미경 사진을 출판했는데, 그는 달이 자체적으로 중력을 가지고 있어야 한다고 가정했습니다.[25] 1666년, 그는 두 가지 원칙을 더 추가했습니다: 모든 물체는 어떤 힘에 의해 굴절될 때까지 직선으로 움직인다는 것과 가까운 물체일수록 인력이 더 강하다는 것입니다. 1666년 왕립학회에 보낸 교신에서 후크는[26]

저는 지금까지 받아온 어떤 시스템과도 매우 다른 세계의 시스템을 설명하겠습니다. 다음과 같은 위치에 기반을 두고 있습니다. 1. 모든 천체는 자신의 고유한 중심에 대한 부분의 인력을 가지고 있을 뿐만 아니라 자신의 활동 영역 내에서 서로를 끌어당긴다는 것. 2. 단순한 운동을 하는 모든 물체는 원, 타원 또는 다른 곡선을 묘사하도록 하는 어떤 외부 힘에 의해 지속적으로 편향되지 않는 한 직선으로 계속 움직일 것입니다. 3. 이 매력은 몸이 가까울수록 훨씬 더 큽니다. 그 힘들이 거리의 증가에 의해 감소하는 비율에 관해서는, 나는 그것을 발견하지 못했다는 것을 알고 있습니다.

후크의 1674년 그레샴 강연 "지구의 연간 운동을 증명하기 위한 시도"는 중력이 "모든 천체"에 적용된다고 설명했습니다.[27]

영국의 물리학자이자 수학자인 아이작 뉴턴 경 (1642–1727)

1684년 뉴턴은 에드먼드 핼리에게 "궤도에 있는 물체의 운동에 관하여"라는 제목의 원고를 보냈는데, 이 원고는 케플러의 행성 운동 법칙에 대한 물리적인 정당성을 제공했습니다.[28] 핼리는 이 원고에 감명을 받아 뉴턴에게 이 원고를 확대할 것을 촉구했고, 몇 년 후 뉴턴은 '자연철학의 수학적 원리'라는 획기적인 책을 출판했습니다. 이 책에서 뉴턴은 중력을 보편적인 힘으로 설명하고 "행성을 궤도에 유지시키는 힘은 행성이 회전하는 중심에서 거리의 제곱으로 상호 작용해야 한다"고 주장했습니다. 이 문장은 나중에 다음과 같은 역제곱 법칙으로 요약되었습니다.

여기서 F는 힘, m과 m은 상호작용하는 물체의 질량, r은 질량 중심 사이의 거리, G는 중력 상수 6.674×10 m ⋅ kg ⋅입니다.

뉴턴의 프린시피아는 과학계의 호평을 받았고, 그의 중력 법칙은 순식간에 유럽 전역으로 퍼져나갔습니다.[30] 한 세기 이상이 지난 1821년, 그의 중력 이론은 해왕성의 존재를 예측하는 데 사용되었을 때 훨씬 더 큰 명성을 얻었습니다. 그해 프랑스 천문학자 알렉시스 부바르는 이 이론을 이용해 천왕성의 궤도를 모형화한 표를 만들었고, 이 표는 행성의 실제 궤도와 크게 다르다는 것을 보여주었습니다. 이러한 불일치를 설명하기 위해, 많은 천문학자들은 천왕성의 궤도 너머에 큰 물체가 있을 것이라고 추측했습니다. 1846년 천문학자 존 카우치 애덤스와 어베인 르 베리에는 각각 뉴턴의 법칙을 이용해 밤하늘에서 해왕성의 위치를 예측했고, 그 행성은 하루 만에 그곳에서 발견되었습니다.[31]

일반 상대성 이론

참고 항목: 일반상대성이론 소개
일반 상대성 이론
Spacetime curvature schematic
기본개념
현상
시공간
  • 등식
  • 형식주의
등식
형식주의
고급이론
솔루션
사이언티스트

결국, 천문학자들은 수성의 궤도에서 이심률이 발견되었는데, 이는 뉴턴의 이론으로는 설명할 수 없는 것이었습니다: 궤도의 근일점은 한 세기에 약 42.98 아크초씩 증가하고 있었습니다. 이 불일치에 대한 가장 명확한 설명은 아직 발견되지 않은 천체(태양 주위를 수성보다 훨씬 더 가깝게 돌고 있는 행성 등)였지만, 그러한 천체를 찾기 위한 모든 노력은 성과가 없는 것으로 밝혀졌습니다. 마침내 1915년 알버트 아인슈타인은 수성의 궤도를 정확하게 모델링할 수 있는 일반 상대성 이론을 개발했습니다.[32]

일반 상대성 이론에서 중력의 영향은 힘 대신 시공간 곡률에 기인합니다. 아인슈타인은 이 아이디어를 동등성 원리의 형태로 생각하기 시작했는데, 이 발견은 나중에 그가 "내 인생에서 가장 행복한 생각"이라고 묘사했습니다.[33] 이 이론에서 자유낙하는 관성 운동과 동등한 것으로 간주되며, 이는 자유낙하하는 관성 물체가 지면의 비 관성 관측자에 비해 가속된다는 것을 의미합니다.[34][35] 뉴턴 물리학과는 달리 아인슈타인은 물체에 아무런 힘을 가하지 않고도 이 가속도가 일어나는 것이 가능하다고 믿었습니다.

아인슈타인은 시공간은 물질에 의해 휘어져 있으며, 자유 낙하하는 물체는 휘어진 시공간에서 국부적으로 직선 경로를 따라 이동한다고 제안했습니다. 이 직선 경로를 측지선이라고 합니다. 뉴턴의 제1운동법칙과 마찬가지로 아인슈타인은 물체에 가해지는 힘이 물체를 측지선에서 벗어나게 할 것이라고 믿었습니다. 예를 들어, 지구 표면에 서 있는 사람들은 지구의 기계적 저항이 그들에게 상승력을 가하기 때문에 측지 경로를 따라가는 것이 방지됩니다. 이것은 시공간에서 측지선을 따라 움직이는 것이 관성으로 간주되는 이유를 설명합니다.

중력에 대한 아인슈타인의 설명은 이전에 당황스러웠던 실험 결과들을 매우 다양하게 설명할 수 있었기 때문에 대다수의 물리학자들은 빠르게 받아들여졌습니다.[36] 앞으로 몇 년 동안, 광범위한 실험들이 일반 상대성 이론의 아이디어에 추가적인 지지를 제공했습니다.[37][38][39][40] 뉴턴의 역제곱 법칙은 여전히 유용하고 상당히 정확한 근사치로 남아 있지만, 오늘날 아인슈타인의 상대성 이론은 절대적인 정밀도가 필요한 모든 중력 계산에 사용됩니다.[41]

현대연구

현대 물리학에서 일반 상대성 이론은 중력을 이해하는 틀로 남아 있습니다.[42] 물리학자들은 일반 상대성 이론의 기초를 이루는 아인슈타인 장 방정식의 해결책을 찾기 위해 계속 노력하고 있는 반면, 일부 과학자들은 일반 상대성 이론이 특정 시나리오에서는 전혀 적용되지 않을 수도 있다고 추측했습니다.[41]

아인슈타인 장방정식

아인슈타인 필드 방정식은 물질이 시공간의 곡률에 어떻게 영향을 미치는지 설명하는 10개의 편미분 방정식 체계입니다. 시스템은 종종 형태로 표현됩니다.

여기서 G는 아인슈타인 텐서, g는 메트릭 텐서, T는 응력-에너지 텐서, λ는 우주, G G}는 뉴턴 상수 c c}는 빛의 속도입니다. 상수 κ = π G c 4 {\ \ = 8\pi G} {c^{4}}}}을 아인슈타인 중력 상수라고 합니다.

질량을 가진 구형, 대전되지 않은, 회전하지 않는 물체 주변의 시공간을 설명하는 슈바르츠실트 메트릭의 예시

주요 연구 분야는 아인슈타인 필드 방정식에 대한 정확한 해를 발견하는 것입니다. 이러한 방정식을 푸는 것은 특정 물리적 조건에서 메트릭 텐서(시공간의 곡률과 기하학적 구조를 정의함)에 대한 정확한 값을 계산하는 것과 같습니다. 무엇이 그러한 해결책을 구성하는지에 대한 공식적인 정의는 없지만 대부분의 과학자들은 기본 함수 또는 선형 미분 방정식을 사용하여 표현할 수 있어야 한다는 데 동의합니다.[45] 이 방정식의 가장 주목할 만한 해결책은 다음과 같습니다.

  • 슈바르츠실트 해는 회전하지 않고 대전되지 않은 거대한 물체를 둘러싼 시공간을 설명합니다. 충분히 작은 물체의 경우 이 솔루션은 중심 특이점을 가진 블랙홀을 생성했습니다.[46] 중심 질량에서 멀리 떨어진 지점에서는 슈바르츠실트 해가 예측한 가속도가 뉴턴의 중력 이론이 예측한 가속도와 거의 일치합니다.[47]
  • 전하를 띤 회전하지 않는 구형 대칭 물체를 분석하는 라이스너-노르트스트롬 해는 1916년에서 1921년 사이에 여러 다른 연구자들에 의해 독립적으로 발견되었습니다.[48] 경우에 따라 이 솔루션은 이중 사건 지평선을 가진 블랙홀의 존재를 예측할 수 있습니다.[49]
  • 슈바르츠차일드 해를 회전하는 거대한 물체에 일반화하는 커 해. 회전 효과를 아인슈타인 필드 방정식에 인수분해하는 것이 어렵기 때문에, 이 해는 1963년까지 발견되지 않았습니다.[50]
  • 전하를 띠고 회전하는 거대한 물체를 위한 커-뉴먼 솔루션입니다. 이 해는 1964년에 Kerr 해에 사용된 것과 동일한 복잡한 좌표 변환 기법을 사용하여 도출되었습니다.[51]
  • 1922년 알렉산더 프리드만이 발견한 우주론적 프리드만-르마 î트르-로버트슨-워커 해는 1927년 조르주 르마 î트르에 의해 확인되었습니다. 이 해법은 우주의 팽창을 예측하는 데 혁명적이었고, 에드윈 허블의 일련의 측정 끝에 7년 후에 확인되었습니다.[52] 심지어 일반 상대성 이론은 정적인 우주와 양립할 수 없다는 것을 보여주었고, 아인슈타인은 나중에 팽창하지 않는 우주를 설명하기 위해 자신의 필드 방정식을 설계한 것이 잘못되었음을 인정했습니다.[53]

오늘날 아인슈타인 장방정식이 풀리지 않은 중요한 상황들이 많이 남아 있습니다. 이 중 가장 중요한 것은 쌍체 문제인데, 이 문제는 상호 작용하는 두 개의 거대한 물체(태양과 지구, 또는 쌍성계의 두 별) 주변의 시공간 기하학에 관한 것입니다. 세 개 이상의 거대한 물체의 상호작용을 고려하면 상황은 더욱 복잡해지며, 일부 과학자들은 아인슈타인 필드 방정식이 이러한 맥락에서 결코 풀리지 않을 것이라고 의심합니다.[54] 그러나 포스트 뉴턴 확장 기법을 사용하여 n체 문제의 필드 방정식에 대한 근사 해를 구성하는 것은 여전히 가능합니다.[55] 일반적으로 아인슈타인 필드 방정식의 극단적인 비선형성 때문에 가장 구체적인 경우를 제외한 모든 경우에 해결하기가 어렵습니다.[56]

중력과 양자역학

주요 기사: 중력자와 양자중력

중력의 영향을 대규모로 예측하는 데 성공했음에도 불구하고 일반 상대성 이론은 궁극적으로 양자 역학과 양립할 수 없습니다. 일반 상대성 이론은 중력을 시공간의 매끄럽고 연속적인 왜곡으로 설명하는 반면, 양자역학은 모든 힘이 양자로 알려진 이산 입자의 교환에서 발생한다고 주장하기 때문입니다. 이 모순은 물리학자들에게 특히 성가신 것인데, 다른 세 가지 기본적인 힘(강력, 약력, 전자기)이 수십 년 전에 양자적 틀과 조화를 이루었기 때문입니다.[57] 이에 따라 현대 연구자들은 중력과 양자역학을 보다 일반적인 틀로 통합할 수 있는 이론을 찾기 시작했습니다.[58]

한 가지 경로는 양자장 이론의 틀에서 중력을 설명하는 것이며, 이는 다른 근본적인 상호작용을 정확하게 설명하는 데 성공했습니다. 전자기력은 가상 광자의 교환에서 발생하며, 중력에 대한 QFT 설명은 가상 중력자의 교환이 있다는 것입니다.[59][60] 이 설명은 고전적 한계에서 일반 상대성 이론을 재현합니다. 그러나 이 접근 방식은 양자 중력에 대한 보다 완전한 이론([61]또는 양자 역학에 대한 새로운 접근 방식)이 필요한 플랑크 길이의 짧은 거리에서는 실패합니다.

2024년 2월 23일, 연구자들은 처음으로 미시적 수준에서 중력을 측정했다는 연구 결과를 보고했습니다.[62][63]

일반 상대성 시험

주요 기사: 일반 상대성 시험

일반 상대성 이론의 예측을 시험하는 것은 역사적으로 어려웠습니다. 왜냐하면 그것들은 작은 에너지와 질량에 대한 뉴턴 중력의 예측과 거의 같기 때문입니다.[64] 그럼에도 불구하고, 개발된 이래로, 지속적인 일련의 실험 결과들이 이 이론을 뒷받침해 왔습니다.[64]

1919년 개기일식은 일반 상대성 이론의 예측을 시험할 수 있는 최초의 기회 중 하나를 제공했습니다.
  • 1919년, 영국의 천체물리학자 아서 에딩턴은 그해 일식 동안 예측된 빛의 중력 렌즈 현상을 확인할 수 있었습니다.[65][66] 에딩턴은 일반 상대성 이론의 예측에 따라 뉴턴의 원근 이론이 예측한 별빛 편향의 두 배를 측정했습니다. 비록 에딩턴의 분석은 나중에 논란이 되었지만, 이 실험은 거의 하룻밤 사이에 아인슈타인을 유명하게 만들었고, 일반 상대성 이론이 과학계에서 널리 받아들여지게 만들었습니다.[67]
  • 1959년 미국 물리학자 로버트 파운드와 글렌 렙카는 감마선을 이용해 중력 시간 팽창 예측을 확인하는 실험을 했습니다. 74피트 높이의 탑 아래로 광선을 보내고 바닥에서 광선의 진동수를 측정함으로써, 과학자들은 빛이 중력원을 향해 이동할 때 적색편이 된다는 것을 확인했습니다. 관측된 적색편이는 또한 중력장이 존재할 때 시간이 더 느리게 흐른다는 아이디어를 뒷받침했습니다.[68]
  • 어윈 1세는 질량이 큰 물체에 가까운 빛이 지나가는 시간 지연을 처음으로 확인했습니다. 1964년 행성간 우주선 신호에서 샤피로.[69]
  • 1971년, 과학자들은 백조자리 은하에서 최초의 블랙홀을 발견했습니다. 이 블랙홀은 더 작은 별을 소비하면서 X선의 폭발을 방출하기 때문에 감지되었고, 백조자리 X-1로 알려지게 되었습니다.[70] 이 발견은 일반 상대성 이론에 대한 또 다른 예측을 확인시켜 주었는데, 아인슈타인의 방정식은 빛이 충분히 크고 작은 물체에서 벗어날 수 없다는 것을 암시했기 때문입니다.[71]
  • 일반 상대성 이론은 중력이 빛과 물질에 똑같이 작용한다는 것을 의미하며, 이는 충분히 무거운 물체가 빛을 휘감고 중력 렌즈를 만들 수 있다는 것을 의미합니다. 이 현상은 1979년 미국 애리조나주 키트피크 국립천문대의 2.1m 망원경을 이용한 관측으로 처음 확인됐는데, 이 망원경에서 은하계 YGKOW G1을 중심으로 빛이 휘어진 같은 퀘이사의 거울 이미지 2장이 포착됐습니다.[72][73]
  • 회전하는 거대한 물체가 그 주위를 시공간적으로 비틀어야 한다는 아이디어인 프레임 드래깅은 2011년 중력 탐사선 B의 결과에 의해 확인되었습니다.[74][75]
  • 2015년 LIGO 관측소는 일반 상대성 이론에 의해 그 존재가 예측된 희미한 중력파를 감지했습니다. 과학자들은 이 파동이 15억 광년 떨어진 곳에서 발생한 블랙홀 합병에서 나온 것으로 믿고 있습니다.[76]

구체적 사항

지구 중력

중력에 의해 자유롭게 낙하할 수 있는 초기 정지 상태의 물체는 경과 시간의 제곱에 비례하는 거리를 떨어 뜨립니다. 이 이미지는 30분의 1초에 걸쳐 있으며 초당 20번의 플래시로 캡처되었습니다.
주요 기사: 지구의 중력

모든 행성체(지구 포함)는 자체 중력장으로 둘러싸여 있으며, 뉴턴 물리학은 모든 물체에 매력적인 힘을 가하는 것으로 개념화할 수 있습니다. 구대칭 행성을 가정할 때, 지표면 위의 어느 특정 지점에서 이 장의 세기는 행성의 질량에 비례하고 물체의 중심에서 거리의 제곱에 반비례합니다.

만약 지구와 비슷한 질량을 가진 물체가 그것을 향해 떨어진다면, 그에 상응하는 지구의 가속도는 관측할 수 있을 것입니다.

중력장의 세기는 그 영향을 받는 물체의 가속도와 수치적으로 같습니다.[77] 지구 표면 근처에 떨어지는 물체의 가속 속도는 위도, 산과 능선과 같은 표면 특징, 그리고 아마도 비정상적으로 높거나 낮은 표면 밀도에 따라 매우 약간 다릅니다.[78] 중량 및 측정을 위해 표준 중력 값은 국제 단위 시스템(SI)에 따라 국제 중량 및 측정국에 의해 정의됩니다.

지구에 작용하는 중력은 (a) 뉴턴의 만유인력 법칙에 따른 중력 인력과 (b) 지구에 묶여 회전하는 기준틀의 선택으로 발생하는 원심력의 두 가지 힘의 결과(벡터 합)입니다.[7] 지구의 자전으로 인한 원심력과 적도의 점들이 지구의 중심에서 가장 멀리 떨어져 있기 때문에 적도에서 중력이 가장 약합니다. 중력은 위도에 따라 달라지며 적도에서는 초속2 약 9.780m에서 극점에서는 초속2 약 9.832m로 증가합니다.[79][80]

기원.

플랑크 시대(우주 탄생 후 최대 10초−43)에 개발된 초기 중력(양자중력, 초중력 또는 중력 특이점의 형태일 가능성이 있음)은 아마도 원시 상태(허위 진공, 양자 진공 또는 가상 입자 등)에서 비롯되었을 것입니다. 알 [4]수 없는 방법으로

중력 복사

LIGO Hanford Observatory
2015년 9월 중력파가 처음 관측된 미국 워싱턴에 위치한 LIGO 핸포드 천문대
본문: 중력파

일반 상대성 이론은 중력 복사를 통해 에너지가 계 밖으로 운반될 수 있다고 예측합니다. 중력 복사에 대한 최초의 간접적인 증거는 1973년 헐스-테일러 쌍성의 측정을 통해서였습니다. 이 계는 서로의 궤도를 돌고 있는 펄서와 중성자별로 구성되어 있습니다. 중력 복사로 인한 에너지 손실량에 대해 일치하는 에너지 손실로 인해 처음 발견된 이후 궤도 주기가 감소했습니다. 이 연구는 1993년 노벨 물리학상을 수상했습니다.[81]

중력 복사에 대한 최초의 직접적인 증거는 2015년 9월 14일 LIGO 검출기에 의해 측정되었습니다. 지구에서 13억 광년 떨어진 두 블랙홀의 충돌 과정에서 방출되는 중력파를 측정했습니다.[82][83] 이 관측은 아인슈타인과 다른 사람들이 그러한 파동이 존재한다는 이론적 예측을 확인시켜줍니다. 또한 빅뱅을 포함한 우주의 중력과 사건의 본질에 대한 실질적인 관찰과 이해의 길을 열어줍니다.[84] 중성자별과 블랙홀 형성은 또한 감지 가능한 양의 중력 복사를 만듭니다.[85] 이 연구는 2017년 노벨 물리학상을 수상했습니다.[86]

중력 속도

본문: 중력의 속도

2012년 12월, 중국의 한 연구팀은 보름달과 초승달 동안 지구 조수의 위상 지연을 측정한 결과 중력 속도가 빛의 속도와 같다는 것을 증명하는 것으로 보인다고 발표했습니다.[87] 이것은 만약 태양이 갑자기 사라진다면, 지구는 빛이 그 거리를 여행하는 데 걸리는 시간인 8분 동안 빈 곳의 궤도를 정상적으로 계속 돌 것이라는 것을 의미합니다. 연구팀의 연구 결과는 2013년 2월 사이언스 회보에 발표되었습니다.[88]

2017년 10월, LIGO와 처녀자리 검출기는 감마선 위성과 같은 방향에서 신호를 보는 광학 망원경으로부터 2초 이내에 중력파 신호를 받았습니다. 이를 통해 중력파의 속도가 빛의 속도와 같다는 것을 확인했습니다.[89]

이상 및 불일치

Gravity 변칙과 혼동하지 마십시오.

적절하게 설명되지 않은 관측 결과가 있는데, 이는 더 나은 중력 이론의 필요성을 가리키거나 다른 방식으로 설명될 수 있습니다.

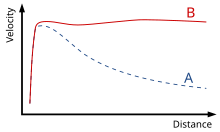
전형적인 나선은하의 회전곡선: 예측(A)과 관측(B). 곡선 사이의 불일치는 암흑 물질에 기인합니다.
  • 초고속 별: 은하계의 별들은 관측된 정상 물질의 분포에 따라 변방의 별들이 필요한 것보다 더 빠르게 움직이는 속도의 분포를 따릅니다. 은하단 내의 은하들도 비슷한 패턴을 보입니다. 중력을 통해 상호 작용하지만 전자기적으로 상호 작용하지 않는 암흑 물질이 이러한 불일치를 설명할 것입니다. 뉴턴 역학에 대한 다양한 수정도 제안되었습니다.
  • 플라이바이 이상: 다양한 우주선이 중력 보조 기동 중에 예상보다 더 큰 가속을 경험했습니다.
  • 가속화된 확장: 우주의 팽창이 빨라지는 것 같습니다.[90] 이를 설명하기 위해 암흑 에너지가 제안되었습니다.[91]
  • 천문 단위의 비정상적인 증가: 최근의 측정 결과에 따르면 행성 궤도는 에너지를 방출함으로써 질량을 잃는 것이 태양을 통해서만 이루어졌을 때보다 더 빠르게 넓어지고 있습니다.
  • 여분의 에너지 광자: 은하단을 통과하는 광자는 에너지를 얻고 나가는 과정에서 다시 에너지를 잃어야 합니다. 우주의 가속 팽창은 광자가 모든 에너지를 되돌려주는 것을 멈추어야 하지만, 이를 고려하더라도 우주 마이크로파 배경 복사의 광자를 고려하면 예상보다 두 배 많은 에너지를 얻을 수 있습니다. 이것은 중력이 특정 거리 척도에서 역제곱보다 더 빨리 떨어짐을 나타낼 수 있습니다.[92]
  • 초대형 수소 구름: 라이먼-알파 숲의 스펙트럼선은 수소 구름이 예상보다 특정 규모에서 더 많이 뭉쳐 있으며 암흑 흐름과 마찬가지로 중력이 특정 거리 규모에서 역제곱보다 더 느리게 떨어지는 것을 나타낼 수 있음을 시사합니다.[92]

대안이론

주요 기사: 일반 상대성 이론의 대안

역사적 대안이론

현대의 대안이론

참고 항목

참고문헌

  1. ^ "dict.cc dictionary :: gravitas :: English-Latin translation". Archived from the original on 13 August 2021. Retrieved 11 September 2018.
  2. ^ Krebs, Robert E. (1999). Scientific Development and Misconceptions Through the Ages: A Reference Guide (illustrated ed.). Greenwood Publishing Group. p. 133. ISBN 978-0-313-30226-8.
  3. ^ "HubbleSite: Black Holes: Gravity's Relentless Pull". hubblesite.org. Archived from the original on 26 December 2018. Retrieved 7 October 2016.
  4. ^ a b – Staff. "Birth of the Universe". University of Oregon. Archived from the original on 28 November 2018. Retrieved 24 September 2016. "플랑크 시간"과 "플랑크 시대"에 대해 우주의 맨 처음에서 논의합니다.
  5. ^ Overbye, Dennis (10 October 2022). "Black Holes May Hide a Mind-Bending Secret About Our Universe - Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos". The New York Times. Retrieved 10 October 2022.
  6. ^ 맥그로-힐 딕트 (1989)
  7. ^ a b Hofmann-Wellenhof, B.; Moritz, H. (2006). Physical Geodesy (2nd ed.). Springer. ISBN 978-3-211-33544-4. § 2.1: "The total force acting on a body at rest on the earth's surface is the resultant of gravitational force and the centrifugal force of the earth's rotation and is called gravity.
  8. ^ Cappi, Alberto. "The concept of gravity before Newton" (PDF). Culture and Cosmos. Archived (PDF) from the original on 9 October 2022.
  9. ^ Bakker, Frederik; Palmerino, Carla Rita (1 June 2020). "Motion to the Center or Motion to the Whole? Plutarch's Views on Gravity and Their Influence on Galileo". Isis. 111 (2): 217–238. doi:10.1086/709138. hdl:2066/219256. ISSN 0021-1753. S2CID 219925047.
  10. ^ Reviel Neitz; William Noel (13 October 2011). The Archimedes Codex: Revealing The Secrets of the World's Greatest Palimpsest. Hachette UK. p. 125. ISBN 978-1-78022-198-4. Archived from the original on 7 January 2020. Retrieved 10 April 2019.
  11. ^ CJ Tuplin, Lewis Wolpert (2002). Science and Mathematics in Ancient Greek Culture. Hachette UK. p. xi. ISBN 978-0-19-815248-4. Archived from the original on 17 January 2020. Retrieved 10 April 2019.
  12. ^ Vitruvius, Marcus Pollio (1914). "7". In Alfred A. Howard (ed.). De Architectura libri decem [Ten Books on Architecture]. Herbert Langford Warren, Nelson Robinson (illus), Morris Hicky Morgan. Harvard University, Cambridge: Harvard University Press. p. 215.
  13. ^ 필로포누스의 자극에 대한 용어는 "ἑνέργεια ἀσώμα τος κινητική"("Incorporal motive energia")이다. CAG XVII, Ioannis Philoponi in Aristotelis Physicorum Libros Quinque Posteriores Commentaria, Walter de Gruyter, 1888, p. 642: "λέγω δὴ ὅτι ἑνέργειά τις ἀσώμα τος κινητικὴ ἑνδίδοτα ι ὑπὸ τοῦ ῥιπτοῦντος τῷ ῥιπτουμένῳ [나는 자극(비인구적 동기 에너지)이 던지는 사람으로부터 던지는 사람에게 전달된다고 말합니다."
  14. ^ Pickover, Clifford (16 April 2008). Archimedes to Hawking: Laws of Science and the Great Minds Behind Them. Oxford University Press. ISBN 9780199792689. Archived from the original on 18 January 2017. Retrieved 29 August 2017.
  15. ^ Bose, Mainak Kumar (1988). Late classical India. A. Mukherjee & Co. Archived from the original on 13 August 2021. Retrieved 28 July 2021.
  16. ^ * Sen, Amartya (2005). The Argumentative Indian. Allen Lane. p. 29. ISBN 978-0-7139-9687-6.
  17. ^ Starr, S. Frederick (2015). Lost Enlightenment: Central Asia's Golden Age from the Arab Conquest to Tamerlane. Princeton University Press. p. 260. ISBN 9780691165851.
  18. ^ Rozhanskaya, Mariam; Levinova, I. S. (1996). "Statics". In Rushdī, Rāshid (ed.). Encyclopedia of the History of Arabic Science. Vol. 2. Psychology Press. pp. 614–642. ISBN 9780415124119.
  19. ^ a b c Wallace, William A. (2018) [2004]. Domingo de Soto and the Early Galileo: Essays on Intellectual History. Abingdon, UK: Routledge. pp. 119, 121–22. ISBN 978-1-351-15959-3. Archived from the original on 16 June 2021. Retrieved 4 August 2021.
  20. ^ Drabkin, I. E. (1963). "Two Versions of G. B. Benedetti's Demonstratio Proportionum Motuum Localium". Isis. 54 (2): 259–262. doi:10.1086/349706. ISSN 0021-1753. JSTOR 228543. S2CID 144883728.
  21. ^ Schilling, Govert (31 July 2017). Ripples in Spacetime: Einstein, Gravitational Waves, and the Future of Astronomy. Harvard University Press. p. 26. ISBN 9780674971660. Archived from the original on 16 December 2021. Retrieved 16 December 2021.
  22. ^ 갈릴레오 (1638), 두 개의 새로운 과학, 첫날 살비아티는 다음과 같이 말합니다. "만약 이것이 아리스토텔레스가 의미했던 것이라면, 당신은 거짓에 해당하는 또 다른 오류를 그에게 부담시킬 것입니다. 왜냐하면, 지구에는 그런 순전한 높이가 없기 때문입니다. 아리스토텔레스는 실험을 할 수 없었을 것이 분명합니다. 그러나 그는 우리가 보는 것과 같은 효과에 대해 말할 때 우리에게 그가 실험을 수행했다는 인상을 주고 싶어합니다."
  23. ^ Gillispie, Charles Coulston (1960). The Edge of Objectivity: An Essay in the History of Scientific Ideas. Princeton University Press. pp. 3–6. ISBN 0-691-02350-6.
  24. ^ J.L. Heilbron, 17세기와 18세기의 전기: 초기근대물리학에 관한 연구 (버클리: 캘리포니아 대학교 출판부, 1979), 180.
  25. ^ 그리빈 & 그리빈(2017), p. 57.
  26. ^ Stewart, Dugald (1816). Elements of the Philosophy of the Human Mind. Vol. 2. Edinburgh; London: Constable & Co; Cadell & Davies. p. 434.
  27. ^ 후크(1679), 지구의 연간 운동을 증명하기 위한 시도, 2, 3페이지
  28. ^ Sagan, Carl & Druyan, Ann (1997). Comet. New York: Random House. pp. 52–58. ISBN 978-0-3078-0105-0. Archived from the original on 15 June 2021. Retrieved 5 August 2021.
  29. ^ "2018 CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 20 May 2019.
  30. ^ "The Reception of Newton's Principia" (PDF). Archived (PDF) from the original on 9 October 2022. Retrieved 6 May 2022.
  31. ^ "This Month in Physics History". www.aps.org. Retrieved 6 May 2022.
  32. ^ Nobil, Anna M. (March 1986). "The real value of Mercury's perihelion advance". Nature. 320 (6057): 39–41. Bibcode:1986Natur.320...39N. doi:10.1038/320039a0. S2CID 4325839.
  33. ^ Webb, Joh; Dougan, Darren (23 November 2015). "Without Einstein it would have taken decades longer to understand gravity". Retrieved 21 May 2022.
  34. ^ "Gravity and Warped Spacetime". black-holes.org. Archived from the original on 21 June 2011. Retrieved 16 October 2010.
  35. ^ Dmitri Pogosyan. "Lecture 20: Black Holes – The Einstein Equivalence Principle". University of Alberta. Archived from the original on 8 September 2013. Retrieved 14 October 2011.
  36. ^ Brush, S. G. (1 January 1999). "Why was Relativity Accepted?". Physics in Perspective. 1 (2): 184–214. Bibcode:1999PhP.....1..184B. doi:10.1007/s000160050015. ISSN 1422-6944. S2CID 51825180.
  37. ^ Lindley, David (12 July 2005). "The Weight of Light". Physics. 16.
  38. ^ "Hafele-Keating Experiment". hyperphysics.phy-astr.gsu.edu. Retrieved 22 May 2022.
  39. ^ "How the 1919 Solar Eclipse Made Einstein the World's Most Famous Scientist". Discover Magazine. Retrieved 22 May 2022.
  40. ^ "At Long Last, Gravity Probe B Satellite Proves Einstein Right". www.science.org. Retrieved 22 May 2022.
  41. ^ a b "Einstein showed Newton was wrong about gravity. Now scientists are coming for Einstein". NBC News. 3 August 2019. Retrieved 22 May 2022.
  42. ^ Stephani, Hans (2003). Exact Solutions to Einstein's Field Equations. Cambridge University Press. p. 1. ISBN 978-0-521-46136-8.
  43. ^ "Einstein Field Equations (General Relativity)". University of Warwick. Retrieved 24 May 2022.
  44. ^ "How to understand Einstein's equation for general relativity". Big Think. 15 September 2021. Retrieved 24 May 2022.
  45. ^ Ishak, Mustafa. "Exact Solutions to Einstein's Equations in Astrophysics" (PDF). University of Texas at Dallas. Archived (PDF) from the original on 9 October 2022. Retrieved 25 May 2022.
  46. ^ "The Schwarzchild Metric and Applications" (PDF). p. 36. Archived (PDF) from the original on 9 October 2022. Retrieved 26 May 2022.
  47. ^ Ehlers, Jurgen (1997). "Examples of Newtonian limits of relativistic spacetimes". Classical Quantum Gravity. 14 (1A): 122–123. Bibcode:1997CQGra..14A.119E. doi:10.1088/0264-9381/14/1A/010. hdl:11858/00-001M-0000-0013-5AC5-F. S2CID 250804865.
  48. ^ "Surprise: the Big Bang isn't the beginning of the universe anymore". Big Think. 13 October 2021. Retrieved 26 May 2022.
  49. ^ Norebo, Jonatan (16 March 2016). "The Reissner-Nordström metric" (PDF). Archived (PDF) from the original on 9 October 2022.
  50. ^ Teukolsky, Saul (1 June 2015). "The Kerr metric" (PDF). Classical and Quantum Gravity. 32 (12): 124006. arXiv:1410.2130. Bibcode:2015CQGra..32l4006T. doi:10.1088/0264-9381/32/12/124006. S2CID 119219499. Archived (PDF) from the original on 9 October 2022.
  51. ^ Newman, E. T.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. (June 1965). "Metric of a Rotating, Charged Mass". Journal of Mathematical Physics. 6 (6): 918–919. Bibcode:1965JMP.....6..918N. doi:10.1063/1.1704351. ISSN 0022-2488. S2CID 122962090.
  52. ^ Pettini, M. "RELATIVISTIC COSMOLOGY" (PDF). Archived (PDF) from the original on 9 October 2022. Retrieved 27 May 2022.
  53. ^ O’Raifeartaigh, Cormac; O’Keeffe, Michael (2017). "Einstein's 1917 Static Model of the Universe: A Centennial Review". The European Physical Journal H. 42 (3): 41. arXiv:1701.07261. Bibcode:2017EPJH...42..431O. doi:10.1140/epjh/e2017-80002-5. S2CID 119461771.
  54. ^ Siegel, Ethan. "This Is Why Scientists Will Never Exactly Solve General Relativity". Forbes. Retrieved 27 May 2022.
  55. ^ Spyrou, N. (1 May 1975). "The N-body problem in general relativity". The Astrophysical Journal. 197: 725–743. Bibcode:1975ApJ...197..725S. doi:10.1086/153562. ISSN 0004-637X.
  56. ^ Sleator, Daniel (6 June 1996). "Hermeneutics of Classical General Relativity". Retrieved 23 May 2022.
  57. ^ "Gravity Probe B – Special & General Relativity Questions and Answers". einstein.stanford.edu. Retrieved 1 August 2022.
  58. ^ Huggett, Nick; Matsubara, Keizo; Wüthrich, Christian (2020). Beyond Spacetime: The Foundations of Quantum Gravity. Cambridge University Press. p. 6. ISBN 9781108655705.
  59. ^ Feynman, R.P.; Morinigo, F.B.; Wagner, W.G.; Hatfield, B. (1995). Feynman lectures on gravitation. Addison-Wesley. ISBN 978-0-201-62734-3.
  60. ^ Zee, A. (2003). Quantum Field Theory in a Nutshell. Princeton University Press. ISBN 978-0-691-01019-9.
  61. ^ Randall, Lisa (2005). Warped Passages: Unraveling the Universe's Hidden Dimensions. Ecco. ISBN 978-0-06-053108-9.
  62. ^ Lea, Robert (23 February 2024). "'Quantum gravity' could help unite quantum mechanics with general relativity at last - "By understanding quantum gravity, we could solve some of the mysteries of our universe — like how it began, what happens inside black holes, or uniting all forces into one big theory."". Space.com. Archived from the original on 24 February 2024. Retrieved 23 February 2024.
  63. ^ Fuchs, Tim M.; et al. (23 February 2024). "Measuring gravity with milligram levitated masses". Science Advances. 10 (8). doi:10.1126/sciadv.adk294. Archived from the original on 24 February 2024. Retrieved 24 February 2024.
  64. ^ a b "Testing General Relativity". NASA Blueshift. Retrieved 29 May 2022.
  65. ^ Dyson, F.W.; Eddington, A.S.; Davidson, C.R. (1920). "A Determination of the Deflection of Light by the Sun's Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919". Phil. Trans. Roy. Soc. A. 220 (571–581): 291–333. Bibcode:1920RSPTA.220..291D. doi:10.1098/rsta.1920.0009. Archived from the original on 15 May 2020. Retrieved 1 July 2019.Dyson, F.W.; Eddington, A.S.; Davidson, C.R. (1920). "A Determination of the Deflection of Light by the Sun's Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919". Phil. Trans. Roy. Soc. A. 220 (571–581): 291–333. Bibcode:1920RSPTA.220..291D. doi:10.1098/rsta.1920.0009. Archived from the original on 15 May 2020. Retrieved 1 July 2019.인용문, p. 332: "따라서 소브랄과 프린시페 원정의 결과는 빛의 편향이 태양 근처에서 일어나고 그것이 태양의 중력장에 기인하는 것처럼 아인슈타인의 일반화된 상대성 이론이 요구하는 양이라는 것을 거의 의심하지 않을 수 있습니다."
  66. ^ Weinberg, Steven (1972). Gravitation and cosmology. John Wiley & Sons. ISBN 9780471925675.인용문, p. 192: "12개의 별들이 모두 연구되었고, 1.98 ± 0.11"과 1.61 ± 0.31"의 값을 산출했으며, 아인슈타인의 예측 θ = 1.75"와 상당히 일치했습니다.
  67. ^ Gilmore, Gerard; Tausch-Pebody, Gudrun (20 March 2022). "The 1919 eclipse results that verified general relativity and their later detractors: a story re-told". Notes and Records: The Royal Society Journal of the History of Science. 76 (1): 155–180. arXiv:2010.13744. doi:10.1098/rsnr.2020.0040. S2CID 225075861.
  68. ^ "General Astronomy Addendum 10: Graviational Redshift and time dilation". homepage.physics.uiowa.edu. Retrieved 29 May 2022.
  69. ^ Asada, Hideki (20 March 2008). "Gravitational time delay of light for various models of modified gravity". Physics Letters B. 661 (2–3): 78–81. arXiv:0710.0477. Bibcode:2008PhLB..661...78A. doi:10.1016/j.physletb.2008.02.006. S2CID 118365884.
  70. ^ "The Fate of the First Black Hole". www.science.org. Retrieved 30 May 2022.
  71. ^ "Black Holes Science Mission Directorate". webarchive.library.unt.edu. Retrieved 30 May 2022.
  72. ^ Subal Kar (2022). Physics and Astrophysics: Glimpses of the Progress (illustrated ed.). CRC Press. p. 106. ISBN 978-1-000-55926-2. 106페이지 발췌
  73. ^ "Hubble, Hubble, Seeing Double!". NASA. 24 January 2014. Retrieved 31 May 2022.
  74. ^ "NASA's Gravity Probe B Confirms Two Einstein Space-Time Theories". Nasa.gov. Archived from the original on 22 May 2013. Retrieved 23 July 2013.
  75. ^ ""Frame-Dragging" in Local Spacetime" (PDF). Stanford University. Archived (PDF) from the original on 9 October 2022.
  76. ^ "Gravitational Waves Detected 100 Years After Einstein's Prediction". LIGO Lab Caltech. Retrieved 30 May 2022.
  77. ^ Cantor, G.N.; Christie, J.R.R.; Hodge, M.J.S.; Olby, R.C. (2006). Companion to the History of Modern Science. Routledge. p. 448. ISBN 978-1-134-97751-2. Archived from the original on 17 January 2020. Retrieved 22 October 2017.
  78. ^ Nemiroff, R.; Bonnell, J., eds. (15 December 2014). "The Potsdam Gravity Potato". Astronomy Picture of the Day. NASA.
  79. ^ Boynton, Richard (2001). "Precise Measurement of Mass" (PDF). Sawe Paper No. 3147. Arlington, Texas: S.A.W.E., Inc. Archived from the original (PDF) on 27 February 2007. Retrieved 22 December 2023.
  80. ^ "Curious About Astronomy?". Cornell University. Archived from the original on 28 July 2013. Retrieved 22 December 2023.
  81. ^ "The Nobel Prize in Physics 1993". Nobel Foundation. 13 October 1993. Retrieved 22 December 2023. for the discovery of a new type of pulsar, a discovery that has opened up new possibilities for the study of gravitation
  82. ^ Clark, Stuart (11 February 2016). "Gravitational waves: scientists announce 'we did it!' – live". the Guardian. Archived from the original on 22 June 2018. Retrieved 11 February 2016.
  83. ^ Castelvecchi, Davide; Witze, Witze (11 February 2016). "Einstein's gravitational waves found at last". Nature News. doi:10.1038/nature.2016.19361. S2CID 182916902. Archived from the original on 12 February 2016. Retrieved 11 February 2016.
  84. ^ "WHAT ARE GRAVITATIONAL WAVES AND WHY DO THEY MATTER?". popsci.com. 13 January 2016. Archived from the original on 3 February 2016. Retrieved 12 February 2016.
  85. ^ Abbott, B. P.; et al. (LIGO Scientific Collaboration & Virgo Collaboration) (October 2017). "GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral" (PDF). Physical Review Letters. 119 (16): 161101. arXiv:1710.05832. Bibcode:2017PhRvL.119p1101A. doi:10.1103/PhysRevLett.119.161101. PMID 29099225. Archived (PDF) from the original on 8 August 2018. Retrieved 28 September 2019.
  86. ^ Devlin, Hanna (3 October 2017). "Nobel prize in physics awarded for discovery of gravitational waves". the Guardian. Archived from the original on 3 October 2017. Retrieved 3 October 2017.
  87. ^ 중국 과학자들이 중력의 속도에 대한 증거를 발견했습니다. 2013년 1월 8일 웨이백 머신(astrowatch.com , 12/28/12)에서 보관되었습니다.
  88. ^ TANG, Ke Yun; HUA ChangCai; WEN Wu; CHI ShunLiang; YOU QingYu; YU Dan (February 2013). "Observational evidences for the speed of the gravity based on the Earth tide". Chinese Science Bulletin. 58 (4–5): 474–477. Bibcode:2013ChSBu..58..474T. doi:10.1007/s11434-012-5603-3.
  89. ^ "GW170817 Press Release". LIGO Lab – Caltech. Archived from the original on 17 October 2017. Retrieved 24 October 2017.
  90. ^ "The Nobel Prize in Physics 2011 : Adam G. Riess Facts". NobelPrize.org. Retrieved 19 March 2024.
  91. ^ "What is Dark Energy? Inside our accelerating, expanding Universe". science.nasa.gov. Retrieved 19 March 2024.
  92. ^ a b Chown, Marcus (16 March 2009). "Gravity may venture where matter fears to tread". New Scientist. Archived from the original on 18 December 2012. Retrieved 4 August 2013.
  93. ^ Brans, C.H. (March 2014). "Jordan–Brans–Dicke Theory". Scholarpedia. 9 (4): 31358. arXiv:gr-qc/0207039. Bibcode:2014Schpj...931358B. doi:10.4249/scholarpedia.31358.
  94. ^ Horndeski, G.W. (September 1974). "Second-Order Scalar–Tensor Field Equations in a Four-Dimensional Space". International Journal of Theoretical Physics. 88 (10): 363–384. Bibcode:1974IJTP...10..363H. doi:10.1007/BF01807638. S2CID 122346086.
  95. ^ Milgrom, M. (June 2014). "The MOND paradigm of modified dynamics". Scholarpedia. 9 (6): 31410. Bibcode:2014SchpJ...931410M. doi:10.4249/scholarpedia.31410.
  96. ^ Haugan, Mark P; Lämmerzahl, C (2011). "Einstein gravity from conformal gravity". arXiv:1105.5632 [hep-th].

원천

추가읽기

외부 링크