토크

토크
토크
	한 평면으로만 제한된 회전을 가진 시스템에서 힘 F, 토크 τ, 선형 운동량 p 및 각 운동량 L 사이의 관계(중력 및 마찰력으로 인한 힘과 모멘트는 고려되지 않음).
공통기호	τ{\},M
SI단위	N ⋅m
기타단위	파운드-포스-feet, lbf ⋅ 인치, ozf ⋅ 인치
SI 기준 단위로	kg ⋅m ⋅
치수	M L2 T−2

물리학과 역학에서 토크는 선형 힘의 회전 유사체입니다.^[1]힘의 모멘트(Moment of force)라고도 합니다.그것은 고립된 물체에 전달될 각운동량의 변화율을 설명합니다.

이 개념은 아르키메데스가 지렛대의 사용에 대한 연구에서 비롯되었는데, 이는 그의 유명한 인용구인 "지렛대와 지구를 움직일 곳을 준다면 지구를 움직일 것입니다."에 반영되어 있습니다.선형 힘이 물체에 가해지는 밀거나 당기는 것처럼 토크는 선택한 지점에 대해 물체에 가해지는 비틀림으로 간주될 수 있습니다.토크는 힘의 수직 성분의 크기와 힘이 결정되는 지점에서 작용선의 거리의 곱으로 정의됩니다.에너지 보존 법칙은 토크를 이해하는 데도 사용될 수 있습니다.토크의 기호는 일반적으로 τ ${\displaystyle {\boldsymbol {\tau}},$ 소문자 그리스 문자 tau입니다.힘의 모멘트라고 할 때 일반적으로 $M$ 으로 표시됩니다.

3차원에서 토크는 의사벡터이며, 점입자의 경우 변위 벡터와 힘 벡터의 교차곱에 의해 제공됩니다.강체에 인가되는 토크의 크기는 인가되는 힘, 토크가 측정되는 지점과 인가되는 지점을 연결하는 레버 암 벡터^[2], 힘과 레버 암 벡터 사이의 각도의 세 가지 양에 따라 달라집니다.기호:

{\bold 기호 {\tau }}=\mathbf {r} \times \mathbf {F}

\tau =rF\sin \theta,

어디에

${\boldsymbol {\tau }}$ $\tau$ {\ $displaystyle {\bold$ $\tau$ }}는 토크 ${\boldsymbol {\tau }}$ 터이고 $\tau$ {\ $displayst$ ${\boldsymbol {\tau }}$ $\tau$ }은 토크의 크기입니다.
$\mathbf {r}$ ${\$ 은 위치 $\mathbf {r}$ 벡터(토크가 측정되는 지점에서 힘이 가해지는 지점까지 벡터)이고, r은 위치 벡터의 크기입니다.
$\mathbf {F}$ ${\$ 는 $\mathbf {F}$ 힘 벡터이고, F는 힘 벡터의 크기,
${\$ 는 오른쪽 규칙에 따라 $r$ 과 $F$ 모두에 수직인 벡터를 생성하는 교차곱을 나타냅니다 $\times$ .
$\theta$ {\ $displaystyle \theta$ }는 $\theta$ 힘 벡터와 레버 암 벡터 사이의 각도입니다.

토크의 SI 단위는 뉴턴 미터(N ⋅m)입니다.토크 단위에 대한 자세한 내용은 § 단위를 참조하십시오.

역사

토크(torque, 라틴어 torque ēre에서 'twist'라는 뜻)라는 용어는 제임스 톰슨이 제안한 것이라고 하며, 1884년 4월에 인쇄에 등장했습니다.Silvanus P는 같은 해에 사용을 검증했습니다. Dynamo-Electric Machinery 초판의 Thompson입니다.^[5]톰슨(Thompson)은 다음과 같이 용어에 동기를 부여합니다.^[4]

힘에 대한 뉴턴의 정의가 (선을 따라) 운동을 일으키거나 만드는 경향이 있는 것처럼, 토크는 (축을 중심으로) 비틀림을 일으키거나 만드는 경향이 있는 것으로 정의될 수 있습니다.더 복잡한 아이디어를 제시하는 "커플"이나 "순간"과 같은 용어를 사용하는 것보다 이 행동을 하나의 확실한 개체로 취급하는 용어를 사용하는 것이 더 좋습니다.축을 회전시키기 위해 적용되는 트위스트의 단일 개념은 일정한 레버리지를 가진 선형 힘(또는 한 쌍의 힘)을 적용하는 더 복잡한 개념보다 더 좋습니다.

오늘날 토크는 지리적 위치와 학문 분야에 따라 다른 어휘를 사용하는 것을 말합니다.이 글은 토크라는 단어를 사용할 때 미국 물리학에서 사용된 정의를 따릅니다.^[6]

영국과 미국의 기계공학에서는 토크를 힘의 모멘트(moment of force)라고 하며, 보통 힘의 모멘트(moment of force)로 줄여서 말합니다.^[7]이 용어는 적어도 시메옹 데니스 푸아송의 트라예 드 메카니크에서 1811년까지 거슬러 올라갈 수 있습니다.^[8]포아송의 작품에 대한 영어 번역본은 1842년에 등장합니다.

각운동량에 대한 정의 및 관계

레버에 수직으로 작용하는 힘은 레버의 지점(레버 암의 길이)으로부터의 거리를 곱한 힘입니다.예를 들어, 지점에서 2미터 떨어진 곳에 작용하는 3뉴턴의 힘은 지점에서 6미터 떨어진 곳에 작용하는 1뉴턴의 힘과 동일한 토크를 발휘합니다.오른손의 손가락이 레버 암 방향에서 힘 방향으로 말려 있으면 엄지가 토크 방향을 가리킵니다.^[9]

일반적으로 점 입자(일부 기준 프레임에서 위치 r)의 토크를 교차 생성물로 정의할 수 있습니다.

{\bold 기호 {\tau }}=\mathbf {r} \times \mathbf {F},

여기서 F는 입자에 작용하는 힘입니다.토크의 크기 τ은 다음과 같습니다.

\tau =rF\sin \theta,

여기서 F는 가해진 힘의 크기이고, θ는 위치와 힘 벡터 사이의 각도입니다.아니면.

\tau =rF_{\perp}

여기서 F는_⊥ 입자의 위치에 수직으로 향하는 힘의 양입니다.입자의 위치 벡터와 평행하게 향하는 힘은 토크를 발생시키지 않습니다.^[10]^[11]

토크 벡터가 위치 벡터와 힘 벡터 모두에 수직이라는 것은 교차 생성물의 특성에서 따옵니다.반대로 토크 벡터는 위치와 힘 벡터가 놓이는 평면을 정의합니다.결과 토크 벡터 방향은 우측 규칙에 의해 결정됩니다.^[10]

물체의 순토크는 물체의 각운동량 변화율을 결정합니다.

{\bold 기호 {\tau }}={\frac {\mathrm {d} \mathbf {L}{\mathrm {d} t}

여기서 L은 각운동량 벡터이고 t는 시간입니다.

점입자의 운동에 대해서는,

\mathbf {L} = I{\bolds 기호 {\omega}},

여기서 $I$ 는 관성 모멘트이고 ω은 궤도 각속도 의사벡터입니다.다음과 같습니다.

{\bold 기호 {\tau }}_{\mathrm {net}}=I_{1}{\dot {\omega_{1}}{\hat {\bold 기호 {e_{1}}}}+I_{2}{\dot {\omega_{2}}{\hat {\bold 기호 {e_{2}}}}}+I_{3}{\dot {\omega_{3}}{\hat {\bold 기호 {e_{3}}}}}+I_{1}\omega_{1}{\frac {d{\hat {\bold 기호 {e_{1}}}}{dt}}+I_{2}\omega_{2}{\frac {d{\hat {\bold 기호 {e_{2}}}}{dt}}+I_{3}\omega_{3}{\frac {d{\hat {\bold 기호 {e_{3}}}}{dt}}=I{\bold 기호 {\vec {\dot {\omega}}}}+{\bold 기호 {\vec {\omega}}}\회(I{\bold 기호 {\vec {\omega}}})

동사의 도함수를 사용하는 것은

{d{\bold 기호 {\hat {e_{i}}}} \overdt}={\vec {\bold 기호 {\omega}}}\times {\hat {e_{i}}

이 방정식은 점 입자에 대한 뉴턴의 제2법칙의 회전 유사체이며, 모든 유형의 궤적에 대해 유효합니다.

회전하는 원반처럼 회전축의 관성 모멘트만 존재하는 단순한 경우에는 회전하는 뉴턴의 제2법칙은 다음과 같습니다.

{\bold 기호 {\tau }}=I{\bold 기호 {\alpha}}

여기서 I =

{\textstyle I=mr^{2}}

{\textstyle I=mr^{2}}

{\textstyle

I =

mr^{2}}

및

{\boldsymbol {\alpha }}={\boldsymbol {\vec {\dot {\omega }}}}

= ω ˙

{\boldsymbol {\alpha}

=

{\bec {\dot {\omega}}}.

정의 등가성의 증명

단일 점 입자에 대한 각운동량의 정의는 다음과 같습니다.

\mathbf {L} =\mathbf {r} \times \mathbf {p}

여기서 p는 입자의 선형 운동량이고 r은 원점으로부터의 위치 벡터입니다.이것의 시간 미분은 다음과 같습니다.

{\frac {\mathrm {d} \mathbf {L} {\mathrm {d} t}}=\mathbf {r} \t} \times {\frac {\mathrm {d} t} + {\frac {\mathrm {d} \mathbf {r} {\mathrm {d} t} \times \mathbf {p} \times \mathbf {p} \times \mathrm {p

이 결과는 벡터를 구성 요소로 나누고 제품 규칙을 적용하면 쉽게 증명할 수 있습니다.이제 force ${\textstyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}}$ = ${\textstyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}}$ ${\textstyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}}$ ${\textstyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}}$ ${\textstyle \mathbf {F}$ = {\ $frac {\mathrm {d} \mathrm {p}$ } ${\mathrm {d}$ t $}($ 질량이 일정한지 여부에 관계없이)의 정의와 속도 ${\textstyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\mathbf {v} }$ ${\textstyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\mathbf {v} }$ ${\textstyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\mathbf {v} }$ ${\textstyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\mathbf {v} }$ = ${\textstyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\mathbf {v} }$ ${\textstyle {\mathrm {r} \mathbf$ {r} ${\mathrm {d}$ t} =\ $mathbf {v} }$

{\frac {\mathrm {d} \mathbf {L} {\mathrm {d} t} =\mathbf {r} \times \mathbf {F} +\mathbf {v} \times \mathbf {p} .

운동량 $\mathbf {p}$ ${\$ 과 $\mathbf {p}$ (와) $\mathbf {v}$ 된 $속도$ v {\ $displaystyle$ \mathbf ${v}}$ 의 교차곱은 속도와 운동량이 평행하므로 0이므로 $\mathbf {v}$ 두 번째 항이 사라집니다.

정의에 따라 토크 τ = r × F.따라서 입자의 토크는 시간에 대한 각운동량의 1차 도함수와 같습니다.

만약 여러 힘이 작용한다면, 뉴턴의 제2법칙은 대신 F = ma라고 읽으며, 다음과 같습니다.

{\frac {\mathrm {d} \mathbf {L} {\mathrm {d} t} =\mathbf {r} \times \mathbf {F} _{\mathrm {net} = {\bold 기호 {\tau }_{\mathrm {net}}

점 입자에 대한 일반적인 증거입니다.

증명은 위의 증명을 각 점 입자에 적용한 후 모든 점 입자를 합산함으로써 점 입자 시스템으로 일반화될 수 있습니다.마찬가지로, 증명은 질량 내의 각 점에 위의 증명을 적용한 후, 전체 질량에 걸쳐 적분함으로써 연속 질량으로 일반화될 수 있습니다.

유닛

토크는 힘의 시간 거리 차원, 상징적으로 TLM을⁻²² 갖습니다.이러한 기본 치수는 에너지 또는 일에 대한 치수와 동일하지만, 공식 SI 문헌은 뉴턴 미터(N ⋅m) 단위를 사용하고 줄을 사용하지 말 것을 제안합니다.뉴턴 미터 단위는 N ⋅m으로 적절히 표시됩니다.

전통적인 임페리얼 및 미국의 토크 단위는 파운드 풋(lbf-ft) 또는 작은 값의 파운드 인치(lbf-in)입니다.미국에서 토크는 가장 일반적으로 발-파운드(lb-ft 또는 ft-lb로 표시됨)와 인치-파운드(in-lb로 표시됨)로 불립니다.^[14]^[15]실무자들은 문맥과 약어의 하이픈에 의존하여 이러한 것들이 에너지 또는 질량 모멘트가 아닌 토크를 가리킵니다(상징 ft-lb가 적절하게 의미하는 바와 같이).

특례 기타 사실

모멘트 암 공식

물리학 이외의 분야에서 토크의 정의로 종종 주어지는 매우 유용한 특수한 경우는 다음과 같습니다.

{\displaystyle \tau =({\text{moment암}})({\text{force}).

오른쪽 그림에는 위에서 언급한 벡터 r과 F와 함께 "모멘트 암"의 구성이 나와 있습니다.이 정의의 문제점은 토크의 방향을 제시하지 않고 크기만을 제시하기 때문에 3차원적인 경우에는 사용하기 어렵다는 것입니다.힘이 변위 벡터 r에 수직이면 모멘트 암은 중심까지의 거리와 같고 토크는 주어진 힘에 대해 최대가 됩니다.수직력에서 발생하는 토크의 크기에 대한 방정식:

\tau =({\text{distance to center}})({\text{force}).

예를 들어, 사람이 0.5m 길이의 렌치 말단에 10N의 힘(또는 렌치의 비틀림 지점으로부터 0.5m 작용하는 10N의 힘)을 가하면 토크는 5N ⋅m이 됩니다. 이는 사람이 렌치에 수직하고 이동면에서 힘을 가해 렌치를 움직인다고 가정한 것입니다.

서로 반대되는 두 힘_g F와 -F에_g 의해 발생하는 토크는 토크 방향으로 **각운동량** L에 변화를 일으킵니다.이로 인해 상단이 눌리게 됩니다.

정적 평형

물체가 정적 평형에 있기 위해서는 힘의 합이 0이어야 할 뿐만 아니라 모든 점에 대한 토크(모멘트)의 합도 0이어야 합니다.수평력과 수직력이 존재하는 2차원 상황의 경우, 필요한 힘의 합은 두 개의 $방정식$ 인 σ $HH$ = $0$ 과 σ $V$ = $0$ 이고, 세 번째 방정식인 토크는 σ τ = $0$ 입니다.즉, 정적으로 결정된 평형 문제를 2차원으로 풀기 위해 3개의 방정식을 사용합니다.

순력 대 토크

시스템에 작용하는 순력이 0일 때 공간의 어느 지점에서 측정한 토크는 동일합니다.예를 들어, 균일한 자기장에서 전류 전달 루프의 토크는 기준 시점에 관계없이 동일합니다.알짜힘 $\mathbf {F}$ $\mathbf {F}$ 가 0이 아니고, τ ${\boldsymbol {\tau }}_{1}$ ${\displaystyle$ ${\$ $tau$ $}}$ $_{1}$ 에서 $\mathbf {r} _{1}$ 한 $\mathbf {r} _{1}$ 토크가 r 1 {\ $displaystyle$ \ $mathbf$ { $r}_{$ 1}에서 측정한 $\mathbf {r} _{1}$ $\mathbf {r} _{2}$ 라면 $,$ r 2 {\ $displaystyle$ \ $mathbf {r}$ _{2}에서 측정한 토크는

{\bold 기호 {\tau }}_{2}={\bold 기호 {\tau }}_{1}+(\mathbf {r} _{1}-\mathbf {r} _{2})\times \mathbf {F}

기계토크

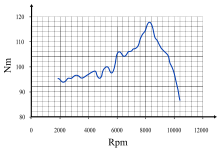
토크는 엔진의 기본 사양 중 일부를 구성합니다. 엔진의 출력은 토크에 구동축의 각속도를 곱한 값으로 표시됩니다.내연 기관은 제한된 회전 속도 범위(보통 소형차의 경우 약 1,000~6,000rpm)에서만 유용한 토크를 생성합니다.동력계로 해당 범위에서 다양한 토크 출력을 측정하여 토크 곡선으로 나타낼 수 있습니다.

증기 엔진과 전기 모터는 0rpm에 가까운 최대 토크를 생성하는 경향이 있으며, 회전 속도가 증가함에 따라 토크가 감소합니다(마찰 증가 및 기타 제약으로 인해).왕복 증기 기관과 전기 모터는 클러치 없이 0rpm부터 무거운 부하를 시작할 수 있습니다.

토크, 동력, 에너지의 관계

만약 힘이 멀리서 작용하도록 허락된다면, 그것은 기계적인 일을 하는 것입니다.마찬가지로 토크가 각변위를 통해 작용할 수 있도록 허용하면 작업을 수행하는 것입니다.수학적으로, 질량 중심을 통과하는 고정된 축을 중심으로 회전하는 경우, 워크 W는 다음과 같이 나타낼 수 있습니다.

W=\int _{\theta _{1}}^{\theta _{2}}\tau \\mathrm {d} \theta ,

여기서 τ은 토크이고, θ와 θ은 (각각) 차체의 초기 및 최종 각도 위치를 나타냅니다.

증명

유한 선형 변위 ${\displaystyles}$ 에 작용하는 가변 힘에 의해 행해지는 일은 원소 선형 변위 $\mathrm {d} \mathbf {s}$ ${d} \mathbf {s}$ 에 대한 힘을 적분함으로써 주어집니다 $s$ .

W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} \mathbf {s}

그러나, 무한소 선형 변위 $\mathrm {d} \mathbf {s}$ $\mathrm {d} \mathbf {s}$ 는 대응하는 각 변위 $\mathrm {d} {\boldsymbol {\theta }}$ θ $\mathrm {d} {\boldsymbol {\theta}$ 와 반지름 $\mathbf {r}$ r $\mathbf {r$ 과(와) 관련이 있습니다.

\mathrm {d} \mathbf {s} =\mathrm {d} {\bold 기호 {\theta}}\times \mathbf {r}

작업에 대한 위 식의 대체는 다음과 같습니다.

W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} {\bold 기호 {\theta}}\times \mathbf {r}

식 $\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r}$ ⋅ $\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r}$ θ $\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r}$ x r ${\displaystyle \mathbf {F} \cdot \mathrm {d} {\$ bold $기호 {\theta}}\times \mathbf {r}}$ 는 [ $\left[\mathbf {F} \,\mathrm {d} {\boldsymbol {\theta }}\,\mathbf {r} \right]$ θ ${\displaystyle$ \ $left[\mathbf {F} \,\mathrm {d} {\bold$ 기호 ${\theta}}\,\mathbf {r} \right]}$ 에서 주어진 스칼라 삼중곱입니다 $\left[\mathbf {F} \,\mathrm {d} {\boldsymbol {\theta }}\,\mathbf {r} \right]$ 동일한 스칼라 삼중곱에 대한 대체 식을 다음과 같습니다.

\left[\mathbf {F} \,\mathrm {d} {\bold 기호 {\theta}}\,\mathbf {r} \right]=\mathbf {r} \times \mathbf {F} \cdot \mathrm {d} {\bold 기호 {\theta}}

하지만 토크의 정의에 의하면,

{\bold 기호 {\tau }}=\mathbf {r} \times \mathbf {F}

업무의 표현에 있어서 그에 상응하는 대체성은,

W=\int _{s_{1}}^{s_{2}}{\bold 기호 {\tau }}\cdot \mathrm {d}{\bold 기호 {\theta}}

적분의 파라미터가 선형변위에서 각도변위로 변경되었기 때문에 적분의 한계 또한 상응하게 변경되어 다음을 제공합니다.

W=\int _{\theta _{1}}^{\theta _{2}}{\bold 기호 {\tau }}\cdot \mathrm {d}{\bold 기호 {\theta}

토크와 각도 변위가 같은 방향이면, 스칼라 곱은 크기의 곱으로 줄어듭니다. 즉, τ ⋅ ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$ θ = τ ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$ θ ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$ ⁡ ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$ = ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$ τ ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$ θ ${\displaystyle {\boldsymbol {\$ tau }\ $cdot \mathrm {d} {\boldsymbol {\theta$ }}=\ $left {\boldsymbol {\$ tau }\ $right \mathrm {d} {\boldsymbol {\theta }}\right \cos$ 0 = $\,$ $\mathrm {d} \theta}$ 제공 ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$

W=\int _{\theta _{1}}^{\theta _{2}}\tau \,\mathrm {d} \theta

일 에너지 원리에 따르면 W는 또한 다음과 같이 주어진 물체의_r 회전 운동 에너지 E의 값은 다음과 같습니다.

E_{\mathrm {r} = {\tfrac {1}{2}}I\omega^{2},

여기서 I는 신체의 관성모멘트이고 ω은 각속도입니다.

전력은 단위 시간당 작업이며, 다음과 같이 제공됩니다.

P={\bolds 기호 {\tau }}\cdot {\bolds 기호 {\omega}}},

여기서 P는 거듭제곱, τ는 토크, ω는 각속도, ⋅ $\cdot$ 는 스칼라 곱을 나타냅니다.

대수학적으로 방정식은 주어진 각속도와 출력에 대한 토크를 계산하도록 재배치될 수 있습니다.토크에 의해 주입되는 동력은 토크가 인가되는 동안 각속도가 증가, 감소 또는 일정하게 유지되는지의 여부가 아닌 순간 각속도에만 의존합니다(이는 힘에 의해 주입되는 동력이 결과적인 가속도에 의존하지 않고 순간 속도에만 의존하는 선형적인 경우와 같습니다).tion(있는 경우).

실제로 자전거에서 이러한 관계를 관찰할 수 있습니다.자전거는 일반적으로 2개의 로드 휠, 체인에 맞물리는 전후 기어(sprrockets로 지칭됨) 및 자전거의 변속 시스템이 복수의 기어비를 사용할 수 있게 하는 경우(즉, 멀티 스피드 자전거), 그리고 프레임에 모두 부착되는 경우, 데레일러 메커니즘(derailure mechanism)으로 구성됩니다.자전거를 타는 사람인 자전거 운전자는 페달을 돌리면서 입력 동력을 제공하여 앞 스프로켓(일반적으로 체인 링이라고 함)을 크랭크합니다.자전거 운전자가 제공하는 입력 동력은 각속도(즉, 분당 페달 회전수 2 π)와 자전거 크랭크셋의 스핀들 토크의 곱과 같습니다.자전거의 드라이브트레인은 입력된 전력을 로드 휠에 전달하고, 로드 휠은 수신된 전력을 자전거의 출력 전력으로 도로에 전달합니다.자전거의 기어비에 따라 (토크, 각속도)_input 쌍이 (토크, 각속도)_output 쌍으로 변환됩니다.더 큰 리어 기어를 사용하거나 다단 자전거에서 저단 기어로 전환하면 토크가 증가하는 동안 로드 휠의 각속도가 감소하며, 그 중 제품(즉, 동력)은 변하지 않습니다.

SI 단위의 경우 동력의 단위는 와트, 토크의 단위는 뉴턴 미터, 각도 속도의 단위는 초당 라디안입니다(rpm이 아니고 초당 회전수가 아님).

뉴턴 미터 단위는 에너지의 단위인 줄과 차원적으로 동등합니다.토크의 경우 단위는 벡터에 할당되지만 에너지의 경우 스칼라에 할당됩니다.이는 전자에서는 뉴턴 미터와 줄의 치수 등가성이 적용될 수 있지만 후자의 경우에는 적용되지 않는다는 것을 의미합니다.이 문제는 라디안을 무차원 단위가 아닌 기본 단위로 취급하는 방향 분석에서 해결됩니다.^[17]

타 단위로의 전환

다른 단위의 동력 또는 토크를 사용할 경우 변환 계수가 필요할 수 있습니다.예를 들어 회전 속도(단위: 분당 회전수 또는 초당 회전수)를 각속도(단위: 초당 라디안) 대신 사용할 경우 회전당 2 π 라디안을 곱해야 합니다.다음 식에서 P는 힘, τ은 토크, ν(그리스 문자 nu)은 회전 속도입니다.

P=\tau \cdot 2\pi \cdot \nu

단위 표시:

P_{\rm {W}}=\tau _{\rm {N{\cdot}m}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/s}

분당 60초로 나누면 다음과 같습니다.

P_{\rm {W}}={\frac {\rm {{\cdot}m}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/min}}{\rm {60~s/min}}

여기서 회전 속도는 분당 회전수(rpm, rev/min)입니다.

일부 사람들(예: 미국 자동차 엔지니어)은 동력을 위해 마력(기계식)을 사용하고, 토크를 위해 풋-파운드(lbf ⋅ft)를 사용하고 회전 속도를 위해 rpm을 사용합니다.그 결과 공식은 다음과 같이 바뀝니다.

P_{\rm {hp}}={\frac {\rm {{lbf{\cdot}ft}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/min}}{33,000}

아래 상수(분당 피트 파운드 단위)는 마력의 정의에 따라 변합니다. 예를 들어 미터법 마력을 사용하면 약 32,550이 됩니다.

다른 장치(예: 전력의 경우 시간당 BTU)를 사용하려면 다른 사용자 지정 변환 계수가 필요합니다.

파생

회전하는 물체의 경우, 회전 둘레에 적용되는 선형 거리는 각도가 적용된 반지름의 곱입니다.즉, 선형 거리 = 반지름 × 각도 거리입니다.그리고 정의에 따라 선형 거리 = 선형 속도 × 시간 = 반경 × 각도 속도 × 시간입니다.

토크의 정의: 토크 = 반경 × 힘.이를 재배열하여 힘 = 토크 ÷ 반경을 결정할 수 있습니다.이 두 가지 값을 검정력의 정의에 대입할 수 있습니다.

{\begin{aligned}{\text{power}}&={\frac {\text{force}}\cdot {\text{time}}\[6pt]&={\frac {\left ({\dfrac {\text{text}}{r}\cdot(r\cdot {\text{text{angular}}\cdot t){t}\[6pt]&={\text{text{torque}}\cdot {\text{text{text}}\cdot {\text{angular}}.\end{aligned}

반지름 r과 시간 t가 방정식에서 빠졌습니다.그러나 각속도는 유도 초기의 선형 속도와 각속도 사이의 가정된 직접적인 관계에 의해 시간 단위당 라디안 단위로 이루어져야 합니다.회전 속도를 시간 단위당 회전수로 측정할 경우, 선형 속도와 거리는 위의 유도에서 비례적으로 2 π 증가하여 다음을 얻을 수 있습니다.

{\text{power}}={\text{torque}}\cdot 2\pi \cdot {\text{rotational speed}}\,

토크가 뉴턴 미터 단위이고 회전 속도가 초당 회전수 단위인 경우 위 식은 초당 뉴턴 미터 단위 또는 와트 단위의 동력을 제공합니다.임페리얼 단위를 사용하고 토크가 파운드 힘 피트, 회전 속도가 분당 회전수인 경우 위의 식은 분당 힘 파운드 힘으로 동력을 제공합니다.그런 다음 변환 계수를 마력당 33,000ft ⋅lbf/min을 적용하여 방정식의 마력 형태를 도출합니다.

{\begin{aligned}{\text{power}}&={\text{torque}}\cdot 2\pi \cdot {\text{회전속도}}\cdot {\frac {\text{ft}}{\text{lbf}}{\text{min}}}\cdot {\frac {\text{lbf}}{\text{ft}}\cdot {33,000\cdot {\text{lbf}}{\text{min}}\[6pt]&\frac {\text{lbf}}\cdot {\text{torque}}\cdot {\text{lbf}}.RPM}}}{{5,252}}\end{aligned}

$5252.113122\approx {\frac {33,000}{2\pi }}.\,$ 는 $5252.113122\approx {\frac {33,000}{2\pi }}.\,$ π를 $5252.113122\approx {\frac {33,000}{2\pi }}.\,$ ≈하기 때문입니다 $5252.113122\approx {\frac {33,000}{2\pi }}.\,$ ${\displaystyle 5252.113122\$ approx ${\frac {33,000}{2\pi}}\,}$

모멘트의 원리

바리뇽 정리(Varignon's theorem)라고도 알려진 모멘트의 원리는 약 1개의 점에 가해지는 여러 힘으로 인한 결과 토크는 기여 토크의 합과 같다는 것입니다.

\tau =\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {r} _{2}+\ldots +\mathbf {r} _{N}\times \mathbf {F} _{N

이로부터 물체의 피벗 주위에서 작용하는 두 힘에 의한 토크는 다음과 같이 균형을 이루게 됩니다.

\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}=\mathbf {0} .

토크 곱셈기

토크는 세 가지 방법을 통해 증가할 수 있습니다. 레버의 길이가 늘어나도록 지점을 위치시키거나, 더 긴 레버를 사용하거나, 속도를 줄이는 기어 세트 또는 기어 박스를 사용합니다.이러한 메커니즘은 회전 속도가 감소함에 따라 토크를 증가시킵니다.

참고 항목

참고문헌

^ 서웨이, R.A.와 주엣 J.J.W. (2003)과학자와 공학자를 위한 물리학.6판브룩스 콜. ISBN 0-534-40842-7.
^ Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.
^ Thomson, James; Larmor, Joseph (1912). Collected Papers in Physics and Engineering. University Press. p. civ.
^ ^a ^b Thompson, Silvanus Phillips (1893). Dynamo-electric machinery: A Manual For Students Of Electrotechnics (4th ed.). New York, Harvard publishing co. p. 108.
^ ^a ^b "torque". Oxford English Dictionary. 1933.
^ Hendricks, Subramony and Van Blerk의 공학 물리학, Chinappi 148페이지, Weblink Archive at the Wayback Machine 2017-07-11
^ 케인, T.R. 케인 그리고 D.A. 레빈슨 (1985).역학, 이론 및 응용 페이지 90-99:무료 다운로드 Wayback Machine에서 2015-06-19 보관.
^ Poisson, Siméon-Denis (1811). Traité de mécanique, tome premier. p. 67.
^ "Right Hand Rule for Torque". Archived from the original on 2007-08-19. Retrieved 2007-09-08.
^ ^a ^b Halliday, David; Resnick, Robert (1970). Fundamentals of Physics. John Wiley & Sons, Inc. pp. 184–85.
^ Knight, Randall; Jones, Brian; Field, Stuart (2016). College Physics: A Strategic Approach. Jones, Brian, 1960-, Field, Stuart, 1958- (Third edition, technology update ed.). Boston: Pearson. p. 199. ISBN 9780134143323. OCLC 922464227.
^ Wayback Machine에서 2021-04-19 공식 SI 웹사이트 Archived 2021-04-19, The International System of Units – 9판 – Text in English 섹션 2.3.4: "...예를 들어, 수량 토크는 위치 벡터와 힘 벡터의 교차곱입니다.SI 단위는 뉴턴 미터입니다.토크가 에너지(SI 단위 줄)와 동일한 차원을 갖더라도 줄은 토크를 표현하는 데 사용되지 않습니다."
^ ^a ^b "SI brochure Ed. 9, Section 2.3.4" (PDF). Bureau International des Poids et Mesures. 2019. Archived (PDF) from the original on 2020-07-26. Retrieved 2020-05-29.
^ "Dial Torque Wrenches from Grainger". Grainger. 2020. 대부분의 미국 산업 환경과 마찬가지로 토크 범위가 lbf-ft가 아닌 ft-lb로 제공됨을 보여주는 시연.
^ Erjavec, Jack (22 January 2010). Manual Transmissions & Transaxles: Classroom manual. p. 38. ISBN 978-1-4354-3933-7.
^ ^a ^b Kleppner, Daniel; Kolenkow, Robert (1973). An Introduction to Mechanics. McGraw-Hill. pp. 267–268. ISBN 9780070350489.
^ Page, Chester H. (1979). "Rebuttal to de Boer's "Group properties of quantities and units"". American Journal of Physics. 47 (9): 820. Bibcode:1979AmJPh..47..820P. doi:10.1119/1.11704.

외부 링크

"마력과 토크" Wayback Machine 2007-03-28 아카이브 파워, 토크 및 기어가 차량의 성능에 어떤 영향을 미치는지 보여주는 기사.
Project PhysNET에서 원운동을 하는 토크와 각운동량
토크의 대화식 시뮬레이션
토크 유닛 변환기
토크에 대한 느낌 Wayback Machine에서 보관된 2021-05-08 규모의 상호작용.

[1] 서웨이, R.A.와 주엣 J.J.W. (2003)과학자와 공학자를 위한 물리학.6판브룩스 콜. ISBN 0-534-40842-7.

[2] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.

[3] Thomson, James; Larmor, Joseph (1912). Collected Papers in Physics and Engineering. University Press. p. civ.

[thompson1-4] Thompson, Silvanus Phillips (1893). Dynamo-electric machinery: A Manual For Students Of Electrotechnics (4th ed.). New York, Harvard publishing co. p. 108.

[oed1933-5] "torque". Oxford English Dictionary. 1933.

[Hendricks-6] Hendricks, Subramony and Van Blerk의 공학 물리학, Chinappi 148페이지, Weblink Archive at the Wayback Machine 2017-07-11

[Kane-7] 케인, T.R. 케인 그리고 D.A. 레빈슨 (1985).역학, 이론 및 응용 페이지 90-99:무료 다운로드 Wayback Machine에서 2015-06-19 보관.

[8] Poisson, Siméon-Denis (1811). Traité de mécanique, tome premier. p. 67.

[9] "Right Hand Rule for Torque". Archived from the original on 2007-08-19. Retrieved 2007-09-08.

[halliday_184-85-10] Halliday, David; Resnick, Robert (1970). Fundamentals of Physics. John Wiley & Sons, Inc. pp. 184–85.

[11] Knight, Randall; Jones, Brian; Field, Stuart (2016). College Physics: A Strategic Approach. Jones, Brian, 1960-, Field, Stuart, 1958- (Third edition, technology update ed.). Boston: Pearson. p. 199. ISBN 9780134143323. OCLC 922464227.

[BIPM222-12] Wayback Machine에서 2021-04-19 공식 SI 웹사이트 Archived 2021-04-19, The International System of Units – 9판 – Text in English 섹션 2.3.4: "...예를 들어, 수량 토크는 위치 벡터와 힘 벡터의 교차곱입니다.SI 단위는 뉴턴 미터입니다.토크가 에너지(SI 단위 줄)와 동일한 차원을 갖더라도 줄은 토크를 표현하는 데 사용되지 않습니다."

[BIPM_5.1-13] "SI brochure Ed. 9, Section 2.3.4" (PDF). Bureau International des Poids et Mesures. 2019. Archived (PDF) from the original on 2020-07-26. Retrieved 2020-05-29.

[GRAINGER-14] "Dial Torque Wrenches from Grainger". Grainger. 2020. 대부분의 미국 산업 환경과 마찬가지로 토크 범위가 lbf-ft가 아닌 ft-lb로 제공됨을 보여주는 시연.

[15] Erjavec, Jack (22 January 2010). Manual Transmissions & Transaxles: Classroom manual. p. 38. ISBN 978-1-4354-3933-7.

[kleppner_267-68-16] Kleppner, Daniel; Kolenkow, Robert (1973). An Introduction to Mechanics. McGraw-Hill. pp. 267–268. ISBN 9780070350489.

[17] Page, Chester H. (1979). "Rebuttal to de Boer's "Group properties of quantities and units"". American Journal of Physics. 47 (9): 820. Bibcode:1979AmJPh..47..820P. doi:10.1119/1.11704.

[1]

[2]

[5]

[4]

[6]

[7]

[8]

[9]

[10]

[11]

[14]

[15]

[17]

Search

토크

네임스페이스

더

목차

역사