벡터의 공분산 및 왜곡
Covariance and contravariance of vectors다변수 대수 및 텐서 분석에서 공분산 및 왜곡 분석은 특정 기하학적 또는 물리적 실체에 대한 양적 설명이 기준의 변화에 따라 어떻게 변화하는지 설명한다.
물리학에서 근거는 때때로 기준 축의 집합으로 생각되기도 한다. 기준 축의 척도 변화는 문제에서 단위의 변화에 해당한다. 예를 들어, 척도를 미터에서 센티미터로 변경함으로써(즉, 기준 축의 척도를 100으로 나눈 값) 측정 속도 벡터의 성분에 100을 곱한다. 벡터는 기준 축에 대한 척도의 변화에 반비례하여 척도를 변화시키는 이러한 동작을 나타내며, 결과적으로 반대라고 불린다. 그 결과 벡터는 다른 단위와의 거리 또는 거리 단위를 갖는 경우가 많다(예를 들어, 속도에는 시간 단위로 나눈 거리 단위가 있다).
대조적으로 탐욕자(이중 벡터라고도 함)는 일반적으로 거리의 역 또는 거리의 역 단위를 다른 단위와 가지고 있다. 코브터의 예로는 공간적 파생상품 또는 거리의−1 단위를 갖는 구배(gradient)가 있다. 탐촉자의 성분은 기준 축의 척도 변화와 같은 방식으로 변화하여 결과적으로 공변량이라고 불린다.
공분산 및 반향성과 관련된 세 번째 개념은 불변성이다. 기준 축의 척도 변화에 따라 변하지 않는 물리적 관측 가능성의 예는 입자의 질량이며 질량 단위(즉, 거리 단위 없음)가 있다. 질량의 단일 스칼라 값은 기준 축의 척도 변화에 독립적이며, 따라서 불변량이라고 불린다.
보다 일반적인 기준 변경 시:
- 반대 벡터 또는 접선 벡터(흔히 방향 벡터 또는 속도 벡터와 같은 벡터로서 간단히 약칭)는 보상할 수 있는 기초의 변화를 수반하여 반대되는 성분을 가지고 있다. 즉 벡터 성분을 변환하는 행렬은 기본 벡터를 변환하는 행렬의 역행렬이어야 한다. 벡터의 구성 요소(욕구의 구성 요소와는 반대)는 반비례적이라고 한다. 반대편 구성요소가 있는 벡터의 예로는 관찰자에 상대적인 물체의 위치 또는 시간에 대한 위치의 파생(속도, 가속도 및 저크 포함)이 있다. 아인슈타인 표기법에서 반대되는 성분은 다음과 같이 상위 지수로 표시된다.
- = 참고: 인덱스 "i"에 대한 암시적 합계)
- 공변량 벡터 또는 등변량 벡터(흔히 코브레이터로 약칭)는 기초의 변화에 따라 공변량 벡터(cubector)를 갖는 성분을 가지고 있다. 즉, 구성요소는 기본 행렬의 변경과 동일한 행렬에 의해 변환되어야 한다. 탐촉자의 성분(벡터의 성분과 반대)은 공변량이라고 한다. 공변 벡터의 예는 함수의 구배를 취할 때 일반적으로 나타난다. 아인슈타인 표기법에서 공변성분은 다음과 같이 낮은 지수로 표시된다.
원통형 좌표나 구형 좌표와 같은 곡선 좌표계는 종종 물리적, 기하학적 문제에 사용된다. 좌표계와 연관된 것은 공간의 각 지점에서 벡터에 대한 좌표계의 자연스러운 선택이며, 공분산 및 편차성은 벡터의 좌표 설명이 좌표계에서 다른 좌표계로 전달함으로써 어떻게 변화하는지 이해하는 데 특히 중요하다.
공변량 및 역변량이라는 용어는 연관된[2][3] 대수적 형태 이론의 맥락에서 1851년 제임스 조셉 실베스터에 의해 도입되었다. 텐서는 공분산과 반비례의 양면을 모두 가질 수 있는 다변형 대수상의 물체다.
범주이론의 어휘에서 공분산 및 왜곡은 펑거스의 성질이다. 불행히도 일반적으로 반대되는 풀백을 갖는 것은 낮은 지수 객체(커버터)이고, 반면 상위 지수 객체(벡터)는 공변량인 푸시포워드(pushpush forwards를 갖는 것은 낮은 지수 객체(커버터)는 공변량이다. 이러한 종말론적 갈등은 "코벡터" 용어와 일치하여 반대편 functor를 "코퍼레이터"라고 부르고 벡터를 개념으로 취급하고 벡터를 코코넛으로 취급하는 전통을 지속함으로써 피할 수 있다.
소개
물리학에서 벡터는 일반적으로 측정의 결과나 일련의 측정의 결과로 발생하며, 다음과 같은 숫자의 목록(또는 튜플)으로 표현된다.
리스트의 숫자는 좌표계의 선택에 따라 달라진다. 예를 들어, 벡터가 관찰자(위치 벡터)에 대한 위치를 나타내는 경우, 구성 요소1 v, v2 및 v가3 측정되는 강체 로드 시스템 또는 기준 축에서 좌표계를 구할 수 있다. 벡터가 기하학적 객체를 나타내려면 다른 좌표계에서 벡터가 어떻게 보이는지 설명할 수 있어야 한다. 즉 벡터의 구성요소는 한 좌표계에서 다른 좌표계로 전달하면서 특정한 방식으로 변모할 것이다.
역방향 벡터에는 좌표 변화(따라서 기준 축의 변환과 반비례)에 따라 회전과 확장을 포함하여 "좌표와 같이 변환"되는 구성 요소가 있다. 벡터 자체는 이러한 연산 하에서 변하지 않는다. 대신, 벡터의 구성요소는 공간 축의 변화를 취소하는 방식으로, 변화를 좌표로 하는 것과 같은 방식으로 변화한다. 즉, 기준 축을 한 방향으로 회전시키면 벡터의 성분 표현은 정확히 반대 방향으로 회전하게 된다. 마찬가지로 기준 축이 한 방향으로 늘어나면 좌표와 마찬가지로 벡터의 구성요소가 정확히 보상되는 방식으로 감소할 것이다. Mathematically, if the coordinate system undergoes a transformation described by an invertible matrix M, so that a coordinate vector x is transformed to , then a contravariant vector v must be similarly transformed via 이 중요한 요건은 물리적으로 의미 있는 양의 다른 세 배와 반대되는 벡터를 구별하는 것이다. 예를 들어, v가 속도의 x-, y-, z- 성분으로 구성되면 v는 반대 방향 벡터: 공간의 좌표가 늘어나거나 회전하거나 꼬이면 속도의 구성요소가 같은 방식으로 변환된다. 반대 벡터의 예로는 위치, 변위, 속도, 가속도, 운동력 및 힘이 포함된다.
대조적으로 공변량 벡터에는 좌표와 반대로 변화하거나, 동등하게 기준 축과 같이 변환하는 성분이 있다. 예를 들어, 함수의 그라데이션 벡터 구성 요소
기준 축 그 자체처럼 변형한다.
정의
공분산 및 반향성의 일반적인 공식은 좌표 벡터 구성요소가 기반 변화(수동적 변환) 하에서 어떻게 변모하는지를 가리킨다. 따라서 V를 스칼라 S의 영역 위에 치수 n의 벡터 공간이 되게 하고, f = (X1, ..., Xn)와 f′ = (Y1, ..., Y)의n 각각을 V의 기초가 되게 한다.[note 1] 또한 f에서 f로 근거의 변경은 다음에 의해 주어지게 한다.
-
(1)
을(를) 입력하는 일부 반전성 n×n 매트릭스 A에 대해 여기서 f′ basis의 각 벡터j Y는 fbasis의 벡터 X의i 선형 결합이므로 다음과 같이 된다.
역반변형
V의 벡터 은(는) f 기준의 X 요소의 선형 조합으로 고유하게 표현된다.
-
(2)
여기서 vi[f]는 f basis에서 v의 구성 요소로 알려진 (알제브라틱) 필드 S의 요소다. v의 구성 요소 열 벡터를 v[f]로 나타냄:
(2)가 매트릭스 제품으로 다시 작성될 수 있도록
벡터 v는 f′ basis 단위로도 표현될 수 있으므로 다음과 같다.
단, 벡터 v 자체는 기본의 선택에 따라 불변하므로,
f와 f의 관계 (1)과 결합된 v의 불변성은 다음을 함축한다.
변환 규칙 제공
구성 요소 면에서는
여기서 계수 ~ 는 A의 역행렬 항목이다.
벡터 v의 성분은 행렬 A의 역행과 함께 변하기 때문에, 이러한 성분은 근간의 변화 하에서 역행적으로 변한다고 한다.
A가 두 쌍을 연결하는 방법은 화살표를 사용하여 다음 비공식 도표에 표시된다. 화살표가 반전된 것은 다음과 같은 상반된 변화를 나타낸다.
공변량 변환
V에 대한 선형 함수 α는 f의 성분(S의 원소)으로 고유하게 표현된다.
이러한 성분은 f basis의 basic 벡터 X에i 대한 α의 작용이다.
기초가 f에서 f to(1)로 바뀌면 성분이 변하여 다음과 같이 된다.
-
(3)
α 성분의 행 벡터를 α[f]만큼 나타냄:
(3)이 매트릭스 제품으로 다시 작성될 수 있도록
선형 기능 α의 성분은 행렬 A와 함께 변환하기 때문에, 이러한 성분은 기초의 변화 하에서 공변적으로 변환한다고 한다.
A가 두 쌍을 연결하는 방법은 화살표를 사용하여 다음 비공식 도표에 표시된다. 화살표가 동일한 방향으로 이동하기 때문에 공변량 관계가 표시된다.
만약 기둥 벡터 표현을 대신 사용한다면, 변환 법칙은 전치법이 될 것이다.
좌표
벡터 공간 V에 대한 basic f의 선택은 V에 대한 좌표함수의 집합을 다음과 같은 방법으로 고유하게 정의한다.
따라서 V의 좌표는 다음과 같은 점에서 반대다.
반대로, V의 좌표i x처럼 변형되는 n개의 수량i v의 시스템은 반대 방향 벡터를 정의한다. 좌표와 정반대로 변하는 n개의 수량의 시스템은 공변 벡터다.
이러한 왜곡과 공분산의 공식은 벡터가 접선 벡터 또는 등선 벡터로 사는 좌표 공간(다지관)이 있는 용도에서 더 자연스러운 경우가 많다. 다지관의 로컬 좌표계 x가i 주어진 경우 좌표계의 기준 축은 벡터 필드임
이렇게 하면 좌표 패치의 모든 점에서 프레임 f = (X1, ..., Xn)가 발생한다.
y가i 다른 좌표계인 경우
f' 프레임은 좌표 전환의 자코비안 행렬의 역행렬에 의해 f 프레임과 연관된다.
또는, 지수에서,
접선 벡터는 정의상 좌표 부분 s/ 의 선형 조합인 벡터다 따라서 접선 벡터는 다음과 같이 정의된다.
그러한 벡터는 프레임의 변화에 반비례한다. 좌표계의 변화 아래에서는
따라서 접선 벡터 변환의 구성 요소는
따라서 한 좌표계로부터 다른 좌표계로 전달하면서 이런 식으로 변환되는 좌표에 따라 n개의 수량이 v인i 시스템을 역행 벡터라고 한다.
미터법을 사용하는 벡터의 공변량 및 역변량 성분
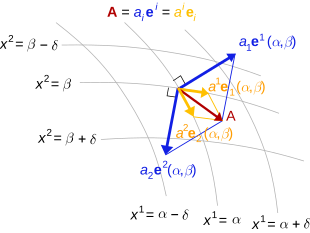
대칭 이선형태가 g : V × V → K (측정지표 텐서라고 할 수 있음)인 필드 K 위에 있는 유한차원 벡터 공간 V에서는, 이선형태가 탐촉자를 벡터로 식별할 수 있게 해주기 때문에 공변성 벡터와 반변성 벡터의 구분이 거의 없다. 즉, 벡터 v는 코브터 α를 통해 고유하게 결정한다.
모든 벡터 w에 대해 반대로 각 코브터 α는 이 방정식에 의해 고유한 벡터 v를 결정한다. 탐촉자가 있는 벡터의 이러한 식별 때문에, 어떤 이는 벡터의 공변성 성분이나 역변성 요소를 말할 수 있다. 즉, 그것들은 상호적 근거를 사용하는 동일한 벡터의 표현일 뿐이다.
V의 basis1 f = (Xn, ..., X)가 주어지면, 다음과 같은 것을 요구하여 결정된 V의 고유한 역수 basis f# = (Y1, ..., Yn)가 있다.
크로네커 삼각주 이러한 베이스의 관점에서 어떤 벡터 v는 다음과 같은 두 가지 방법으로 쓰여질 수 있다.
성분 vi[f]는 basic f에서 벡터 v의 역변성 성분이며, 성분i v[f]는 basic f에서 v의 공변성 성분이다. 그 용어는 근거가 바뀌면
유클리드 평면
유클리드 평면에서 도트 제품은 벡터를 탐촉자로 식별할 수 있게 한다. , e1},\{e2}}이 기본이라면 이중 기준 , }}이 충족됨
따라서 e와1 e는2 e와2 e와1 같이 서로 수직이며 e와1 e의 길이는 각각 e와1 e에2 대해2 정규화된다.
예
예를 들어,[4] 우리에게 기본1 e가 주어진다고 가정해 보자. e는21 길이 2를, e는2 길이 1을 갖는 등 서로 45° 각도를 이루는 벡터 쌍으로 구성되어 있다. 그 후 듀얼 베이시스 벡터는 다음과 같이 주어진다.
- e는2 e를1 90°의 각도로 회전시킨 다음(쌍1 e, e가2 포지티브 방향이라고 가정하여 감지 측정), e2 ⋅ e2 = 1이 고정되도록 재조정하는 결과물이다.
- e는1 e를2 90°의 각도로 회전시킨 다음1 e e1 e = 1이 지탱하도록 다시 정렬하는 결과물이다.
이 규칙들을 적용하면
그리고
따라서 원래의 기초에서 상호 기초로 이동하는 기본 행렬의 변경은 다음과 같다.
그 이후
예를 들어 벡터
역행성 성분의 벡터
공변량 성분은 벡터 v:
그렇게
입체 유클리드 공간
3차원 유클리드 공간에서는 반드시 직교 또는 단위 규범이라고 가정하지 않는 E의3 e의23 주어진 기본 벡터 집합에1 대한 이중 기준을 명시적으로 결정할 수도 있다. 이중 기준 벡터는 다음과 같다.
e와i e가i 정형화되어 있지 않더라도, 그들은 여전히 상호 호혜적이다.
그런 다음 벡터 V의 반대되는 구성 요소는 듀얼 베이시스 벡터를 사용하여 v의 도트 곱으로 얻을 수 있다.
마찬가지로 v의 공변량 성분은 basic 벡터, viz를 사용하여 v의 도트 제품에서 얻을 수 있다.
그러면 v는 두 가지(리시프로칼) 방식으로 표현될 수 있다, viz.
또는
위의 관계를 종합해 보면,
그리고 우리는 기초와 이중의 기초 사이를 전환할 수 있다.
그리고
기본 벡터가 직교인 경우, 이중 기본 벡터와 동일하다.
일반 유클리드 공간
보다 일반적으로, n차원 유클리드 공간 V에서는, 기초가 다음과 같은 경우.
역수 기준은 다음과 같다(이중 지수를 종합한다).
여기서 계수 g는ij 의 역행렬의 항목이다.
정말이지, 우리에겐
벡터의 공변성분 및 역변성분
에 의해 위와 같은 관계가 있다.
그리고
비공식적 사용법
물리학 분야에서는 형용사 공변량이 불변성의 동의어로 비공식적으로 사용되는 경우가 많다. 예를 들어 슈뢰딩거 방정식은 특수상대성이론의 좌표변환 아래에 서면 형태를 유지하지 않는다. 따라서 물리학자는 슈뢰딩거 방정식이 공변량이 아니라고 말할지도 모른다. 대조적으로, 클라인-고든 방정식과 디락 방정식은 이러한 좌표 변환 하에서 서면 형태를 유지한다. 따라서 물리학자는 이 방정식들이 공변량이라고 말할지도 모른다.
이러한 '공변량'의 사용에도 불구하고, 클라인-고든 방정식과 디라크 방정식은 불변성이며, 슈뢰딩거 방정식은 불변성이 아니라고 하는 것이 더 정확하다. 또한 모호성을 제거하기 위해 불변성을 평가하는 변환을 표시해야 한다.
벡터의 성분은 반비례적이며 탐욕자의 성분은 공변성이기 때문에 벡터 자체는 반비례적이며 탐욕자체는 공변량이라고 하는 경우가 많다.
텐서 분석 시 사용
공분산과 편차의 구별은 종종 분산이 혼합된 텐서를 가진 계산에 특히 중요하다. 이는 공변성분과 반동성분 또는 벡터성분과 코브터성분 모두를 가지고 있다는 것을 의미한다. 텐서(tensor)의 용어는 변종 및 공변량 용어의 수인데, 아인슈타인 표기법에서 공변량 성분은 지표가 낮은 반면, 반변량 성분은 지표가 높은 편이다. 공분산과 반향성의 이중성은 벡터나 텐서 수량이 그 구성요소로 표현될 때마다 개입하지만, 현대의 미분 기하학은 텐서를 나타내기 위해 보다 정교한 인덱스프리 방법을 사용한다.
텐서 분석에서 공변량 벡터는 해당 반대방향 벡터에 대해 다소 호혜적으로 변화한다. 벡터 공간에 있는 물체의 길이, 면적 및 부피에 대한 표현은 공변량 및 역변동 지수를 갖는 텐서 단위로 제공할 수 있다. 좌표의 단순한 팽창과 수축에서는 상호성이 정확하다; 수축하에서는 공변량과 대립적 표현 사이에서 벡터 혼합의 구성요소가 변형된다.
다지관에서 텐서 필드는 일반적으로 아인슈타인 표기법이 널리 사용되는 다중, 상한 및 하한 지수를 가진다. 다지관이 미터법을 갖추게 되면 공변량 지수와 역변량 지수는 서로 매우 밀접한 관계가 된다. 역변동 지수는 미터법 텐서(tensor)와 계약하여 공변량 지수로 전환할 수 있다. 역방향은 미터법 텐서의 (매트릭스) 역방향으로 수축함으로써 가능하다. 일반적으로 미터법 텐서가 부여되지 않은 공간에는 이러한 관계가 존재하지 않는다는 점에 유의하십시오. 더욱이, 좀 더 추상적인 관점에서, 텐서는 단순히 "거기"이며, 그 두 종류의 구성 요소는 선택된 좌표에 따라 값이 달라지는 석회화 공예품일 뿐이다.
기하학적 용어로 설명하자면, 일반 텐서는 탄젠트 번들뿐만 아니라 접선 번들에도 살고 있는 부분이 있기 때문에 공변 지수뿐만 아니라 왜곡 지수를 가질 것이라는 것이다.
A contravariant vector is one which transforms like , where are the coordinates of a particle at its proper time . A covariant vector is one which transforms like {\ x 여기서 은(는) 스칼라 필드다.
대수학 및 기하학
범주론에는 공변성 펑거와 역변성 펑거가 있다. 벡터 공간에 대한 이중 공간의 배정은 역행성 펑터의 표준 예다. 다변수 대수의 일부 구조는 "혼합" 분산으로 되어 있어 펑거가 되는 것을 방지한다.
미분 기하학에서 접선 번들의 기초에 상대적인 벡터의 구성요소는 기초의 변경과 동일한 선형 변환으로 변경되는 경우 공변량이다. 역변환에 의해 변하면 역변성이 있다. 이것은 때때로 두 가지 뚜렷하지만 관련된 이유 때문에 혼란의 원인이 된다. 첫째는 공변량인 벡터(코브터 또는 1형식이라고 함)가 실제로 매끄러운 기능 하에서 뒤로 당겨지는 것으로, 이는 매끄러운 다지관에 코브터의 공간을 할당하는 조작이 실제로는 상쇄적인 펑터라는 것을 의미한다. 마찬가지로, 구성 요소가 반대인 벡터는 매끄러운 매핑 아래에서 앞으로 밀고 나가므로 (반전) 벡터의 공간을 매끄러운 다지관에 할당하는 작업은 공변성 펑터(functor)이다. 둘째, 미분 기하학에 대한 고전적 접근법에서 가장 원시적인 대상인 접선다발의 기초가 아니라 좌표계의 변화다. 반대 성분의 벡터는 좌표의 변화와 같은 방식으로 변한다(이는 실제로 유도된 기준의 변화에 반대하여 변하기 때문이다). 마찬가지로 공변량 성분이 있는 벡터는 좌표의 변화로 인해 반대로 변한다.
참고 항목
메모들
인용구
- ^ C. Misner; K.S. Thorne; J.A. Wheeler (1973). Gravitation. W.H. Freeman & Co. ISBN 0-7167-0344-0.
- ^ 실베스터, 제임스 조셉 "관련 대수형식의 일반 이론에 대해서." 케임브리지와 더블린 수학. Journal, VI(1851): 289-293.
- ^ 1814-1897., Sylvester, James Joseph (2012). The collected mathematical papers of James Joseph Sylvester. Volume 3, 1870-1883. Cambridge: Cambridge University Press. ISBN 978-1107661431. OCLC 758983870.CS1 maint: 숫자 이름: 작성자 목록(링크)
- ^ Bowen, Ray (2008). "Introduction to Vectors and Tensors" (PDF). Dover. pp. 78, 79, 81.[영구적 데드링크]
참조
- Kusse, Bruce R.; Erik A., Westwig (2010), Mathematical Physics: Applied Mathematics for Scientists and Engineers (2nd ed.), Germany: Wiley, ISBN 978-3-527-61814-9.
- Arfken, George B.; Weber, Hans J. (2005), Mathematical Methods for Physicists (6th ed.), San Diego: Harcourt, ISBN 0-12-059876-0.
- Dodson, C. T. J.; Poston, T. (1991), Tensor geometry, Graduate Texts in Mathematics, 130 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-52018-4, MR 1223091.
- Greub, Werner Hildbert (1967), Multilinear algebra, Die Grundlehren der Mathematischen Wissenschaften, Band 136, Springer-Verlag New York, Inc., New York, MR 0224623.
- Sternberg, Shlomo (1983), Lectures on differential geometry, New York: Chelsea, ISBN 978-0-8284-0316-0.
- 실베스터, JJ.(1853년),"그 Syzygetic 관계 2의 합리적 적분 함수의 이론, 슈투름의 함수론에 대한 적용 포함, 그리고 그일의 가장 위대한 Algebraical 공통 측정"(PDF), 왕립 학회 런던의 왕립 학회의 철학 연보(PhilosophicalTransations)143:407–548, doi:10.1098/rstl.1853.0018, JSTOR 10.8572.
외부 링크
- "Covariant tensor", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- "Contravariant tensor", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Covariant Tensor". MathWorld.
- Weisstein, Eric W. "Contravariant Tensor". MathWorld.
- 인바리언스, 컨트라바언스 및 공분산
- 텐서 미적분학 소개---Kees Dullemond & Kasper Peeters











 벡터
벡터 
![{\displaystyle v=\sum _{i}v^{i}[\mathbf {f} ]X_{i},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90b72abefff4c45053a324fb2fb787cf3218e4d8)
![\mathbf{v}[\mathbf{f}] = \begin{bmatrix}v^1[\mathbf{f}]\\v^2[\mathbf{f}]\\\vdots\\v^n[\mathbf{f}]\end{bmatrix}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afc428882c2502b9b82f8e88856bb8985f1836bb)
![v = \mathbf{f}\, \mathbf{v}[\mathbf{f}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/38d62c1fce2d588ff5543c46b26b15d354db8e7b)
![v = \mathbf{f'}\, \mathbf{v}[\mathbf{f'}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/f24c4af1d82c8bba470455e014d188cb989085c9)
![\mathbf{f}\, \mathbf{v}[\mathbf{f}] = v = \mathbf{f'}\, \mathbf{v}[\mathbf{f'}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f6ae22d1881c5be8c2e435fd3810a23551dda3d)
![\mathbf{f}\, \mathbf{v}[\mathbf{f}] = \mathbf{f}A\, \mathbf{v}[\mathbf{f}A],](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3962d1a863f65b032f3b7d5a05175eac62af5bf)
![{\displaystyle \mathbf {v} [\mathbf {f'} ]=\mathbf {v} [\mathbf {f} A]=A^{-1}\mathbf {v} [\mathbf {f} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6630fe6471c5410ab309a1c0ab87c7223b5464e7)
![v^i[\mathbf{f}A] = \sum_j \tilde{a}^i_jv^j[\mathbf{f}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/36ca85c58ceffe95646387b0e4db8ca41c7d0e28)

![{\displaystyle {\begin{aligned}\mathbf {f} &\longrightarrow \mathbf {f'} \\v[\mathbf {f} ]&\longleftarrow v[\mathbf {f'} ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5d2943b0ec7e69cb464eb00796b0bff1d69a0f0)
![\alpha(X_i) = \alpha_i[\mathbf{f}] , \quad i=1,2,\dots,n.](https://wikimedia.org/api/rest_v1/media/math/render/svg/78cef0e07edd6ef776ee9446d8b5657e8cc60714)
![{\displaystyle {\begin{aligned}\alpha _{i}[\mathbf {f} A]&=\alpha (Y_{i})\\&=\alpha \left(\sum _{j}a_{i}^{j}X_{j}\right)\\&=\sum _{j}a_{i}^{j}\alpha (X_{j})\\&=\sum _{j}a_{i}^{j}\alpha _{j}[\mathbf {f} ].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5108f395d252d83e9807163d455396219f58838)
![\mathbf{\alpha}[\mathbf{f}] = \begin{bmatrix}\alpha_1[\mathbf{f}],\alpha_2[\mathbf{f}],\dots,\alpha_n[\mathbf{f}]\end{bmatrix}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0247136386ed2b4d1f43e74799c7f407e11ed256)
![\alpha[\mathbf{f}A] = \alpha[\mathbf{f}]A.](https://wikimedia.org/api/rest_v1/media/math/render/svg/436acd9e89552942c6d549a6a038ca9937d8b7c8)
![{\displaystyle {\begin{aligned}\mathbf {f} &\longrightarrow \mathbf {f'} \\\alpha [\mathbf {f} ]&\longrightarrow \alpha [\mathbf {f'} ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c04607cbf2bfc1a7da5b554f0420330d1f74b79)
![\alpha^\mathrm{T}[\mathbf{f}A] = A^\mathrm{T}\alpha^\mathrm{T}[\mathbf{f}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/16f71a15d988fc7aaedf7dc061404b7fcbabd86d)
 = v^i[\mathbf{f}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf418accb17eaa6ed703c602ee0d86c16f3f7b20)
![x^i[\mathbf{f}A] = \sum_{k=1}^n \tilde{a}^i_kx^k[\mathbf{f}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/d965941430a4a727c5f692ca8e41f85be625e9e5)





![v = \sum_{i=1}^n v^i[\mathbf{f}] X_i = \mathbf{f}\ \mathbf{v}[\mathbf{f}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7f4bfe3855fb91cf213b8e6c7e4a7dbede12dd3)
![{\displaystyle \mathbf {v} \left[\mathbf {f} '\right]=\mathbf {v} \left[\mathbf {f} J^{-1}\right]=J\,\mathbf {v} [\mathbf {f} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab62393cdc939fedcec59eb7945ffc07a8a6e79d)
![{\displaystyle v^{i}\left[\mathbf {f} '\right]=\sum _{j=1}^{n}{\frac {\partial y^{i}}{\partial x^{j}}}v^{j}[\mathbf {f} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea205057474e8e596a9406f07597320be1e4a660)


![\begin{align}
v &= \sum_i v^i[\mathbf{f}]X_i = \mathbf{f}\,\mathbf{v}[\mathbf{f}]\\
&=\sum_i v_i[\mathbf{f}]Y^i = \mathbf{f}^\sharp\mathbf{v}^\sharp[\mathbf{f}].
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6538d5f776d3947fd2ed6d5db54be5e071b900ac)
![\mathbf{v}[\mathbf{f}A] = A^{-1}\mathbf{v}[\mathbf{f}],\quad \mathbf{v}^\sharp[\mathbf{f}A] = A^T\mathbf{v}^\sharp[\mathbf{f}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bca970af95f22780bfba49634b4e6a701098e32)






![{\displaystyle [\mathbf {e} ^{1}\ \mathbf {e} ^{2}]=[\mathbf {e} _{1}\ \mathbf {e} _{2}]{\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}&2\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5846e698a99413b0601d451ac86e543924a4544)



























