원운동
Circular motion| 시리즈의 일부 |
| 고전 역학 |
|---|
물리학에서, 원형 운동은 원의 둘레를 따라 물체를 움직이거나 원형 경로를 따라 회전하는 것이다.일정한 각도 회전 속도와 일정한 속도로 균일할 수도 있고 변화하는 회전 속도에 따라 균일하지 않을 수도 있습니다.3차원 물체의 고정 축을 중심으로 회전하는 것은 그 부분의 원형 운동을 수반한다.운동방정식은 물체의 질량중심의 움직임을 묘사한다.원형 운동에서는 물체와 표면의 고정점 사이의 거리가 동일하게 유지됩니다.
원형운동의 예로는 일정한 높이에서 지구를 도는 인공위성, 허브 주위를 도는 천장팬의 날개, 로프에 묶여 원을 그리며 회전하는 돌, 경주 트랙의 곡선을 도는 자동차, 균일한 자기장에 수직으로 움직이는 전자, 그리고 내 안에서 회전하는 기어가 있다.채널리즘
물체의 속도 벡터는 끊임없이 변화하기 때문에 움직이는 물체는 회전 중심 방향으로 구심력에 의해 가속된다.이 가속이 없다면, 그 물체는 뉴턴의 운동 법칙에 따라 직선으로 움직일 것이다.
균일한 원운동
물리학에서, 균일한 원형 운동은 일정한 속도로 원형 경로를 가로지르는 물체의 움직임을 묘사한다.본체는 원형 운동을 나타내기 때문에 회전축으로부터의 거리는 항상 일정하게 유지됩니다.물체의 속도는 일정하지만 속도는 일정하지 않다: 벡터량인 속도는 물체의 속도와 이동 방향에 따라 달라진다.이 변화 속도는 가속도의 존재를 나타냅니다. 이 구심 가속도는 일정한 크기이며 항상 회전 축을 향해 있습니다.이 가속도는 또한 크기가 일정하고 회전 축을 향해 있는 구심력에 의해 생성된다.
경로 반경에 비해 무시할 수 없을 정도로 작지 않은 강체의 고정 축을 중심으로 회전하는 경우, 물체의 각 입자는 동일한 각속도로 균일한 원운동을 나타내지만 축에 대한 위치에 따라 속도와 가속도가 변화한다.
수식
반지름 r의 원에서의 움직임의 경우 원둘레는 C = 2µr이다.1회전 주기가 T이면 각속도라고도 하는 각회전 속도 θ는 다음과 같다.
단위는 라디안/초입니다.원을 이동하는 물체의 속도는 다음과 같습니다.
시간 t에 쓸려나간 각도 θ는 다음과 같습니다.
입자의 각가속도α는 다음과 같다.
균일한 원운동의 경우 α는 0이 됩니다.
방향 변경으로 인한 가속도는 다음과 같습니다.
구심력과 원심력은 가속도를 사용하여 확인할 수도 있습니다.
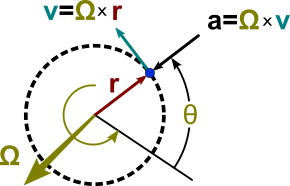
벡터 관계는 그림 1과 같다.회전축은 궤도 평면에 수직인 벡터 θ로 표시되며, 진폭 θ = dθ / dt로 표시된다.②의 방향은 오른쪽 규칙을 사용하여 선택됩니다.회전을 묘사하기 위한 이 규칙에서 속도는 벡터 크로스 곱에 의해 다음과 같이 주어진다.
가장 간단한 경우 속도, 질량 및 반지름은 일정합니다.
반경 1m의 원을 그리며 각 속도가 초당 1라디안인 1kg의 물체를 생각해보자.
- 속도는 초속 1미터입니다.
- 내향 가속도는 평방초당 1미터, v2/r입니다.
- 그것은 평방초당 1킬로그램의 구심력, 즉 1뉴턴의 힘을 받는다.
- 본체의 운동량은 1kg·m·s이다−1.
- 관성 모멘트는 1kg·m이다2.
- 각운동량은 1kg·m2·s이다−1.
- 운동 에너지는 1줄이다.
- 궤도의 둘레는 2µ (~6.283) 미터이다.
- 동작 주기는 회전당 2.5초입니다.
- 주파수는 (2µ)−1헤르츠입니다.
극좌표에서
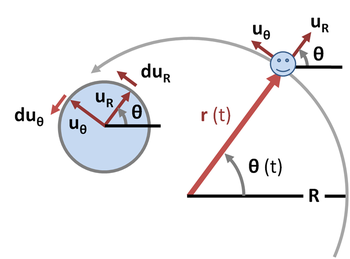
원운동 중 몸은 원점으로 삼은 궤도의 중심에서 일정한 거리 R로 극좌표계에서 묘사될 수 있는 곡선을 따라 움직이며, 기준 방향에서 각도 θ(t)로 방향을 잡는다.그림 4를 참조해 주세요.변위 r(\은 원점에서 입자 위치까지의 반경 벡터입니다.
속도는 변위의 시간 미분입니다.
원의 반지름이 일정하기 때문에 속도의 반지름 성분은 0입니다.단위 ^ R({ { \ } } } {}} if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if if시간 dt에서는 R t도 입니다.\은 dµ 단위 원의 호를 나타냅니다.그림 4의 왼쪽에 있는 단위 원을 참조하십시오.이 때문에,
차체의 가속도는 방사형 및 접선형 구성 요소로 나눌 수도 있습니다.가속도는 속도의 시간 미분입니다.
The time derivative of is found the same way as for . Again, is a unit vector and its tip traces a unit circθ/2 + θ인 각도의 le.r ( t){ \ { } ( ) u u u u^( t) \ \ { } { \ ^^ ^ ^ ^ ^ 、 ^ ^ ^ ( 。{\은 다음과 같습니다.
구심 가속도는 방사상으로 안쪽으로 향하는 반경 성분입니다.
복소수 사용
원운동은 복소수를 사용하여 설명할 수 있다.x축을 실제 축으로 하고을 으로 합니다차체 위치는 복잡한 "벡터"인z\z로 할 수 있습니다.
반지름은 일정하기 때문에:
이 표기법을 사용하면 속도는 다음과 같이 됩니다.
첫 번째 항은 이전 결과와 마찬가지로 변위 벡터와 반대 방향이고 두 번째 항은 이전 결과와 마찬가지로 변위 벡터에 수직입니다.
속도
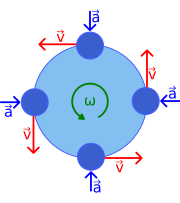
그림 1은 궤도의 4개 지점에서 균일한 움직임을 위한 속도 및 가속도 벡터를 보여줍니다.속도 v는 원형 경로에 접하기 때문에 두 개의 속도가 같은 방향을 가리키지 않습니다.물체는 일정한 속도를 가지고 있지만, 그 방향은 항상 변화합니다.이 속도의 변화는 (속도와 같은) 크기가 일정하지만 방향도 항상 변화하는 가속도 a에 의해 발생합니다.가속점은 방사상으로 안쪽으로(구심적으로) 향하며 속도에 수직입니다.이 가속도를 구심 가속이라고 합니다.
반지름 r의 경로에서 각도 θ가 소거되었을 때 궤도 주변으로 이동한 거리는 s = rθ이다.따라서 궤도를 도는 속도는
상대론적 원운동
이 경우 3가속도 벡터는 3속도 벡터에 수직이다.
액셀러레이션
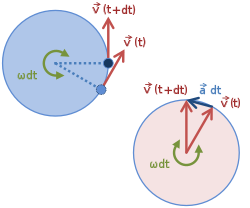
그림 2의 왼쪽 원은 인접한 두 시간에서의 속도 벡터를 보여주는 궤도이다.오른쪽에서, 이 두 가지 속도는 꼬리가 일치하도록 움직입니다.속도가 일정하기 때문에 오른쪽의 속도 벡터는 시간이 지날수록 원을 스위프합니다.sweep angle dθ = a dt의 경우, v의 변화는 v에 대한 직각 및 규모 v dθ의 벡터이며, 이는 가속도의 크기가 다음과 같이 주어진다는 것을 의미한다.
v r | 1 m/s 3.6 km/h 2.2mph | 2 m/s 7.2 km/h 4.5mph | 5 m/s 18 km/h 시속 11마일 | 10 m/s 36 km/h 22mph | 20 m/s 72 km/h 시속 45마일로 | 50 m/s 180 km/h 110mph | 100 m/s 360 km/h 220mph | |
|---|---|---|---|---|---|---|---|---|
| 느린 걸음 | 자전거. | 시티카 | 곡예 비행 | |||||
| 10cm 3.9 인치 | 실험실. 원심 분리기 | 10 m/s2 1.0 g | 40 m/s2 4.1 g | 250 m/s2 25g | 1.0 km/s2 100g | 4.0 km/s2 410 g | 25 km/s2 2500g | 100 km/s2 10000g |
| 20cm 7.9 인치 | 5.0 m/s2 0.51g | 20 m/s2 2.0 g | 130 m/s2 13 g | 500 m/s2 51 g | 2.0 km/s2 200 g | 13 km/s2 1300g | 50 km/s2 5100g | |
| 50cm 1.6피트 | 2.0 m/s2 0.20 g | 8.0 m/s2 0.82g | 50 m/s2 5.1 g | 200 m/s2 20 g | 800 m/s2 82g | 5.0 km/s2 510g | 20 km/s2 2000 g | |
| 1미터 3.3피트 | 놀이터. 회전목마 | 1.0 m/s2 0.10g | 4.0 m/s2 0.41g | 25 m/s2 2.5g | 100 m/s2 10 g | 400 m/s2 41 g | 2.5 km/s2 250 g | 10 km/s2 1000 g |
| 2미터 6.6 피트 | 500 mm/s2 0.051g | 2.0 m/s2 0.20 g | 13 m/s2 1.3 g | 50 m/s2 5.1 g | 200 m/s2 20 g | 1.3 km/s2 130 g | 5.0 km/s2 510g | |
| 5미터 16피트 | 200 mm/s2 0.020 g | 800 mm/s2 0.082g | 5.0 m/s2 0.51g | 20 m/s2 2.0 g | 80 m/s2 8.2g | 500 m/s2 51 g | 2.0 km/s2 200 g | |
| 10미터 33피트 | 롤러코스터 수직 루프 | 100 mm/s2 0.010 g | 400 mm/s2 0.041g | 2.5 m/s2 0.25g | 10 m/s2 1.0 g | 40 m/s2 4.1 g | 250 m/s2 25g | 1.0 km/s2 100g |
| 20미터 66피트 | 50 mm/s2 0.0051 g | 200 mm/s2 0.020 g | 1.3 m/s2 0.13g | 5.0 m/s2 0.51g | 20 m/s2 2 g | 130 m/s2 13 g | 500 m/s2 51 g | |
| 50미터 160피트 | 20 mm/s2 0.0020 g | 80 mm/s2 0.0082g | 500 mm/s2 0.051g | 2.0 m/s2 0.20 g | 8.0 m/s2 0.82g | 50 m/s2 5.1 g | 200 m/s2 20 g | |
| 100미터 330피트 | 고속도로 온스크린 | 10 mm/s2 0.0010 g | 40 mm/s2 0.0041 g | 250 mm/s2 0.025 g | 1.0 m/s2 0.10g | 4.0 m/s2 0.41g | 25 m/s2 2.5g | 100 m/s2 10 g |
| 200미터 660피트 | 5.0 mm/s2 0.00051g | 20 mm/s2 0.0020 g | 130 m/s2 0.013 g | 500 mm/s2 0.051g | 2.0 m/s2 0.20 g | 13 m/s2 1.3 g | 50 m/s2 5.1 g | |
| 500미터 1600 피트 | 2.0 mm/s2 0.00020 g | 8.0 mm/s2 0.00082g | 50 mm/s2 0.0051 g | 200 mm/s2 0.020 g | 800 mm/s2 0.082g | 5.0 m/s2 0.51g | 20 m/s2 2.0 g | |
| 1km 3300피트 | 고속 철도 | 1.0 mm/s2 0.00010 g | 4.0 mm/s2 0.00041 g | 25 mm/s2 0.0025 g | 100 mm/s2 0.010 g | 400 mm/s2 0.041g | 2.5 m/s2 0.25g | 10 m/s2 1.0 g |
균일하지 않다
이 섹션은 Wikipedia 품질 기준에 맞게 다시 작성해야 할 수 있습니다.(2019년 11월) |
비균일한 원형 운동에서 물체는 다양한 속도로 원형 경로로 움직입니다.속도가 변화하고 있기 때문에 정상 가속 외에 접선 가속이 있습니다.
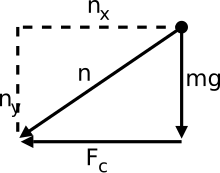
비균일한 원형 운동에서 순가속도 a는 원 안쪽을 향하지만 중심을 통과하지 않는 δv의 방향을 따른다(그림 참조).순가속도는 접선가속도와 구심가속 또는 방사가속이라고도 하는 일반가속도의 두 가지 요소로 분해될 수 있습니다.접선가속도와 달리 구심가속도는 균일하고 균일하지 않은 원형운동으로 존재한다.
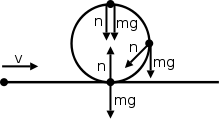
균일하지 않은 원형 운동에서는 정상 힘이 항상 무게의 반대 방향을 가리키지는 않습니다.다음 예에서는 오브젝트가 직선 경로로 이동한 후 루프를 다시 직선 경로로 루프하는 방법을 보여 줍니다.
이 다이어그램은 무게의 반대 방향이 아닌 다른 방향을 가리키는 정상적인 힘을 보여줍니다.법선력은 사실 반지름력과 접선력의 합입니다.중량력의 구성요소는 여기서 접선력에 책임이 있습니다(마찰력을 무시했습니다).방사력(구심력)은 앞서 설명한 속도 방향의 변화에 기인한다.
균일하지 않은 원형 운동에서는 정상적인 힘과 무게가 동일한 방향을 가리킬 수 있습니다.두 힘 모두 아래로 향할 수 있지만, 물체는 똑바로 아래로 떨어지지 않고 원형 경로로 유지됩니다.먼저 왜 정상적인 힘이 처음부터 아래로 향하는지 알아보자.첫 번째 그림에서 물체가 평면 안에 앉아 있는 사람이라고 가정하면 두 힘은 원의 꼭대기에 도달할 때만 아래쪽을 가리킵니다.그 이유는 수직력이 접선력과 구심력의 합이기 때문이다.접선력은 상단에서 0입니다(동작이 가해지는 힘의 방향에 수직인 경우 작업이 수행되지 않으므로).여기서 무게 힘은 원의 꼭대기에 있는 물체의 운동 방향에 수직이며 구심력은 아래를 가리키며, 따라서 정상적인 힘도 아래를 가리키게 됩니다.논리적인 관점에서 보면, 비행기를 타고 여행하는 사람은 원의 맨 위에 거꾸로 서게 될 것이다.그 순간, 그 사람의 의자가 실제로 그 사람을 누르고 있는 것이 정상적인 힘이다.
아래쪽으로만 힘을 가했을 때 물체가 떨어지지 않는 이유는 간단하다.물체가 던져진 후에도 무엇이 물체를 지탱하는지 생각해 보세요.일단 물체가 공중으로 던져지면, 그 물체에 작용하는 지구 중력의 하강력만이 존재한다.그것은 일단 물체가 공중에 던져지면 즉시 낙하한다는 것을 의미하지 않는다.그 물체가 공중에 뜨게 하는 것은 속도이다.뉴턴의 첫 번째 운동 법칙은 물체의 관성이 물체의 움직임을 유지하며, 공기 중의 물체는 속도를 가지고 있기 때문에 그 방향으로 계속 움직이는 경향이 있다고 말한다.
또한 회전체가 균질한 질량 분포를 가지지 않는 경우에는 원형 경로로 이동하는 물체에 대한 가변 각속도를 얻을 수 있다.불균일한 객체의 경우 다음과 [2]같이 문제에 접근해야 합니다.
적용들
비균일한 원형 운동을 다루는 응용 프로그램을 해결하려면 힘 분석이 필요합니다.균일한 원형 운동으로, 원을 따라 이동하는 물체에 작용하는 유일한 힘은 구심력이다.균일하지 않은 원형 운동에서는 접선 가속도가 0이 아니므로 물체에 작용하는 추가 힘이 있습니다.물체에 작용하는 추가적인 힘이 있지만, 물체에 작용하는 모든 힘의 합계는 구심력과 같아야 합니다.
반경 가속은 총 힘을 계산할 때 사용됩니다.접선 가속은 물체를 원형 경로에 유지하는 역할을 하지 않기 때문에 총 힘을 계산하는 데 사용되지 않습니다.물체가 원을 그리며 계속 움직이게 하는 유일한 가속도는 반경 가속도입니다.모든 힘의 합계는 구심력이므로 구심력을 자유체 다이어그램으로 끌어낼 필요가 없으며 일반적으로 권장되지 않는다.
net F {\ F_}}= 물체에 작용하는 모든 힘을 나열하는 자유체도를 그려 F {와 하게 설정할 수 있습니다.그 후 알 수 없는 것(질량, 속도, 곡률 반지름, 마찰계수, 법선력 등)을 해결할 수 있습니다.예를 들어, 반원 맨 위에 있는 물체를 나타내는 위의 은 F n + g \ } =으로 됩니다.
균일한 원운동에서 원경로상의 물체의 총가속도는 반경가속도와 같다.균일하지 않은 원형 운동에서 접선 가속도가 존재하기 때문에 더 이상 해당되지 않습니다.균일한 원형이 아닌 물체의 총 가속도를 찾으려면 접선 가속도와 반지름 가속도의 벡터 합을 구하십시오.
반지름 가속도는 여전히 v {\과 . 접선 가속도는 d t {{t}= frac 의 주어진 지점에서 속도의 파생물일 뿐입니다.별도의 방사 및 접선 가속도의 제곱근 합계는 원형 운동에만 정확합니다. 극좌표 , ) { (, \ )} { c ( ) ( d) \ a { c } \ } { } } 。\를 {{에 해야 합니다 방사 가속은 r - r + 2 { } ={- {{\ {d}} {t}} {t} {t}} {t}} {t} {t} {t} {t} {t}} {t} {t} {t {t}}} {t
「 」를 참조해 주세요.
레퍼런스
- ^ Knudsen, Jens M.; Hjorth, Poul G. (2000). Elements of Newtonian mechanics: including nonlinear dynamics (3 ed.). Springer. p. 96. ISBN 3-540-67652-X.
- ^ Gomez, R W; Hernandez-Gomez, J J; Marquina, V (25 July 2012). "A jumping cylinder on an inclined plane". Eur. J. Phys. IOP. 33 (5): 1359–1365. arXiv:1204.0600. Bibcode:2012EJPh...33.1359G. doi:10.1088/0143-0807/33/5/1359. S2CID 55442794. Retrieved 25 April 2016.
외부 링크
- 물리 클립: 뉴사우스웨일스 대학의 애니메이션과 비디오 클립을 사용한 기계공
- Circular Motion – 온라인 교과서의 한 장
- Circular Motion 강의– CM에 관한 비디오 강의
- [1] – 원형운동에 대한 분석이 다른 온라인 교재















 원점에서 입자 위치까지의 반경 벡터입니다.
원점에서 입자 위치까지의 반경 벡터입니다.













![{\displaystyle z=x+iy=R\left(\cos[\theta (t)]+i\sin[\theta (t)]\right)=Re^{i\theta (t)}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f70473a1d45582449264bfb173bcd862be3dae7)


![{\displaystyle v={\dot {z}}={\frac {d}{dt}}\left(Re^{i\theta [t]}\right)=R{\frac {d}{dt}}\left(e^{i\theta [t]}\right)=Re^{i\theta (t)}{\frac {d}{dt}}\left(i\theta [t]\right)=iR{\dot {\theta }}(t)e^{i\theta (t)}=i\omega Re^{i\theta (t)}=i\omega z}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfe1c9630c24006fe24bf7de9194566b0aff4ca9)