표면의 미분 지오메트리

이 문서는 Surface(수학)에 요약되어 있어야 합니다.#구분이 가능한 표면과 여기서부터 여기까지의 링크를{{Main}} 템플릿입니다. Wikipedia 안내 참조:요약 스타일.(2021년 5월)

수학에서, 표면의 미분 기하학(differential geometry)은 다양한 추가 구조를 가진 매끄러운 표면의 미분 기하학을 다룬다.표면은 다양한 관점에서 광범위하게 연구되어 왔다: 외부적으로는 유클리드 공간에 내장되어 있고 본질적으로 표면상의 곡선을 따라 측정되는 표면 내 거리에 의해서만 결정되는 특성을 반영하고 있다.조사된 기본 개념 중 하나는 칼 프리드리히 ^[1]가우스가 처음으로 깊이 연구한 가우스 곡률이며, 그는 곡률이 유클리드 공간에서의 등각 매립과는 무관한 표면의 고유 특성임을 보여주었다.

표면은 변수 쌍의 함수에 대한 그래프로 자연스럽게 생성되며, 때때로 파라메트릭 형태 또는 공간 곡선과 연관된 궤적으로 나타납니다.그들의 연구에서 중요한 역할은 (에를랑겐 프로그램의 정신으로) 리 그룹, 즉 유클리드 평면, 구 및 쌍곡면의 대칭 그룹에 의해 수행되었다.이러한 Lie 그룹은 일정한 가우스 곡률의 표면을 설명하는 데 사용할 수 있으며, 연결을 통해 본질적인 미분 기하학에 대한 현대적인 접근법에 필수적인 요소를 제공합니다.한편, 유클리드 공간에서의 표면 매립에 의존하는 외인적 특성도 광범위하게 연구되어 왔다.이것은 변동의 미적분학에서 비선형 오일러-라그랑주 방정식에 의해 잘 설명된다: 오일러는 매립과 독립적으로 정의된 측지학을 이해하기 위해 하나의 변수 방정식을 개발했지만, 라그랑주의 두 변수 방정식의 주요 적용 중 하나는 최소 표면에 대한 것이었고, 용어로만 정의될 수 있는 개념이었다.내장되어 있습니다.

역사

혁명의 특정한 2차 곡면 표면의 볼륨 아르키메데스에 의해 계산되지 않았다.[2]미적분학의 17세기의 개발 사업이 자신들에게 컴퓨팅의 더 체계적인 방법을 제공했다.[3]일반 표면의 곡률 먼저 오일러에 의해 연구되었다.1760[4]에, 그는 1771[5]에 표면은 파라메트릭 형태로 표현된 특성을 고려한 표면의 평면 부분의 곡률을 위한 공식을 증명했다.몽주는 1795년에 나타났다 고전 회고록 L'application 드 l'analyse 아 라 géometrie에 그들의 이론의 기초를 내려놓았다.표면의 이론에 결정적인 기여 가우스가 두 사람의 뛰어난 논문은 1825년과 1827년에 쓴에서 만들어졌다.[1]처음으로 가우스 표면의 고유한 기하학, 표면 점을 독립적으로 표면에 주변 유클리드 공간에 위치한 특정 방법 사이의 측지 거리에 의해서만 결정하는 속성을 고려했다 이 전통에서 신기원을 세웠다.그 제일의 결과, 가우스의 빼어난 정리 가우스, 가우스 곡률은 본질적 invariant, i.e. 지역 isometries에도 불변을 설립했다.이 관점은 리만에 의해 고차원 공간으로 확장되었고 오늘날 리만 기하학으로 알려진 것으로 이어졌다.19세기는 대부분의 선도 기하학자들이 연구에 ^{[citation needed]}전념하면서 위상학적, 미분기하학적 관점에서 표면 이론의 황금기였다.다르부스는 그의 4권짜리 논문 Téorie des surfaces (1887–1896)에서 많은 결과를 모았다.

개요

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2020년 8월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

식물의 잎, 유리 표면, 얼굴 모양은 특정한 방식으로 구부러져 있고, 이러한 모든 모양은 구별되는 표시를 무시해도 서로 구별되는 특정한 기하학적 특징을 가지고 있다고 직감적으로 말할 수 있다.표면의 미분 기하학은 그러한 현상에 대한 수학적 이해와 관련이 있다.1700년대에 현대적 형태로 시작된 이 분야의 연구는 리만 기하학과 일반 상대성 ^{[original research?]}이론과 같은 고차원적이고 추상적인 기하학의 발전을 이끌었다.

수학의 본질적인 물체는 정면의 그것이다.규약은 정확한 정의에서 다양하지만, 이것들은 "표면"이라는 익숙한 개념의 일부를 포착하는 3차원 유클리드 공간(δ³)의 일반적인 하위 집합을 형성한다.이러한 표면에 놓여 있는 곡선의 종류와 곡선이 δ³ 단위로 커브되도록 표면이 강제하는 정도를 분석함으로써 주곡선이라고 불리는 두 숫자의 각 점에 연관시킬 수 있다.이들의 평균은 표면의 평균 곡률이라고 불리며, 이들의 곱은 가우스 곡률이라고 불린다.

예를 들어 다음과 같은 일반적인 서페이스의 예가 많이 있습니다.

• 평면, 원통, 구와 같은 친숙한 예
• 최소 표면 - 모든 점에서 평균 곡률이 0이라는 특성에 의해 정의됩니다.가장 잘 알려진 예는 카테노이드와 헬리코이드이지만, 더 많은 것이 발견되었다.최소 표면은 표면적과 관련된 특성에 의해 정의될 수 있으며, 그 결과 와이어 프레임에 걸쳐 늘어났을 때 비누막 모양에 대한 수학적 모델을 제공할 수 있습니다.
• 모든 점을 통과하는 적어도 하나의 직선이 있는 표면으로, 예를 들어 원통 및 한 시트의 쌍곡선이 포함됩니다.

이론으로 알려진 칼 프리드리히 가우스의 놀라운 결과는 표면의 곡선이 3차원 공간에서 어떻게 방향을 바꾸는지와 관련이 있는 표면의 가우스 곡률은 실제로 2cu일 때 만들어진 각도와 함께 표면에 놓여있는 곡선의 길이에 의해 측정될 수 있다는 것을 보여주었다.표면의 갈라진 틈이 교차합니다.용어적으로, 이것은 가우스 곡률이 표면의 첫 번째 기본 형태(미터 텐서라고도 함)에서 계산될 수 있다는 것을 의미합니다.반면 두 번째 기본 형태는 곡선이 표면에서 밀려날 때 곡선의 길이와 각도가 어떻게 왜곡되는지를 인코딩하는 객체입니다.

길이와 각도의 다른 측면을 측정함에도 불구하고, 첫 번째와 두 번째 기본 형태는 서로 독립적이지 않으며, 그것들은 가우스-코다치 방정식이라고 불리는 특정한 제약을 충족합니다.종종 표면의 미분 기하학의 기본 정리라고 불리는 주요 정리는 두 물체가 가우스-코다치 제약 조건을 만족시킬 때마다, 그것들이 규칙 표면의 첫 번째와 두 번째 기본 형태로 나타날 것이라고 주장한다.

첫 번째 기본 형식을 사용하여 일반 표면에서 새 객체를 정의할 수 있습니다.측지학은 첫 번째 기본 형태에 의해 지정된 특정한 2차 상미분 방정식을 만족시키는 표면상의 곡선이다.이들은 곡선의 길이 연구와 매우 직접적으로 연결된다. 충분히 짧은 길이의 측지선은 항상 두 끝점을 연결하는 표면에서 최단 길이의 곡선이 된다.따라서 측지학은 정규 표면에서 주어진 두 점 사이의 최단 경로를 결정하는 최적화 문제에 기초한다.

또한 주어진 곡선을 따라 병렬 전송을 정의할 수 있으며, 이는 곡선의 한 지점에서 표면에 대한 탄젠트 벡터를 곡선의 다른 모든 지점에서 탄젠트 벡터로 변형하는 방법에 대한 처방전을 제공합니다.처방은 1차 상미분방정식에 의해 결정되며, 1차 상미분방정식은 1차 기본형식으로 지정된다.

위의 개념들은 본질적으로 다변수 미적분과 관련이 있다.가우스-보넷 정리는 표면의 가우스 곡률을 위상 유형과 연관짓는 보다 전역적인 결과입니다.그것은 가우스 곡률의 평균값이 표면적과 함께 표면의 오일러 특성에 의해 완전히 결정된다고 주장한다.

리만 다양체의 개념과 리만 표면은 위에서 논의한 정규 표면의 두 가지 일반화이다.특히, 여기서 논의된 모든 규칙적인 표면의 이론은 기본적으로 리만 다양체의 이론에서 일반화를 가지고 있다.모든 정규 표면이 리만 표면의 예를 제공하지만 리만 표면의 경우는 그렇지 않습니다.

유클리드 공간의 규칙적인 표면

정의.

구체는 매끄러운 반면, 꼭지점이나 모서리 때문에 원뿔이나 피라미드는 매끄럽지 않다는 것은 직관적으로 명확합니다."정규 표면"의 개념은 매끄러운 표면의 개념을 공식화한 것입니다.이 정의는 유클리드 공간 사이의 지도를 통해 표면의 국부적 표현을 이용한다.그러한 지도에는 평활성의 표준 개념이 있다; 만약 영역의 ^[6][7][8]모든 점에 모든 차수의 부분 도함수가 존재한다면 유클리드 공간의 두 열린 부분 집합 사이의 지도는 매끄럽다.

다음은 정의를 나타내는 세 가지 동등한 방법을 제시합니다. 중간 정의는 아마도 가장 시각적으로 직관적일 것입니다. 이는 기본적으로 규칙적인 표면이 부드러운 함수의 로컬 그래프(yz 평면, xz 평면 또는 xy 평면의 영역 위)인³ δ의 부분 집합임을 의미하기 때문입니다.

정의에 사용되는 개체	유클리드 공간 δ의3 정규 표면은 δ의3 부분 집합 S이므로 S의 모든 점은 다음을 가진다.
로컬 파라미터화	δ의2 열린 부분집합 V와 동형사상 f : V → U가 존재하는 열린 근방 U δ S는 다음과 같다. 함수 V → δ로서3 f는 무한히 미분할 수 있다(즉, 매끄럽다). V의 각 점에 대하여, 2개의 편도함수 u f와 편도함수 v f는 [9][10][11][12]δ의3 원소로서 선형 독립적이다.
Monge 패치	... 다음 중 하나가 유지되도록 열린 서브셋 V와 평활함수 h : V → ℝ가2 존재하는 열린 근린 U3 ... 。 S u U = {(h(u, v), u, v) : (u, v) v V} S u U = {(u, h(u, v), v) : (u, v) v V} S u U = {(u, v, h(u, v)): (u, v) v V}.
암묵적 함수	...다음과 같은 스무스함수 F : U → ℝ가3 존재하는 열린 근린 U ⊂ ... 。 S u U = {(x, y, z) u U : F(x, y, z) = 0} S u U의 각 점에서 F의 적어도 1개의 편도함수는 0이 아니다.

첫 번째 정의에 나타나는 동형사상은 S ^[13]위의 국소 매개변수화, 국소 좌표계 또는 국소 차트라고 한다.처음 두 정의의 등가성은 규칙적인 표면의 어떤 점 주위에 항상 (u, v) ( (h, v, v), (u, h, v) , (u, h, v), 또는 (u, v) ( (u, v, v) ( (u, v) ( (u, v, v)라고 알려진 형태의 국부 매개변수가 존재한다고 주장한다.세 번째 정의와 같은 함수 F를 로컬 정의 함수라고 합니다.이 세 가지 정의의 등가성은 암묵적 함수 ^[14][15][16]정리에서 비롯된다.

정면의 국소 파라미터화 f : V → U 및 f : : V → → U of of any any any any any any any any any any ⁻¹ any any² subs subs subs subs subs subs subs subs subs subs subs subs subs subs subs subs subs subs subs subs subs ^[17]subs subs subs subs subs subs subs subs subs subs subs이것은 어떤 일반 표면도 자연스럽게 매끄러운 다양체의 구조를 가지고 있으며, 매끄러운 지도는 국소 매개변수화의 역순으로 제공된다는 것을 보여준다.

고전적인 미분 기하학 이론에서 표면은 보통 규칙적인 ^[7][18]경우에만 연구된다.그러나 국소 매개변수화의 두 부분 도함수 _u θf와 _v θf가 선형 독립적이지 않을 수 있는 비정규 표면을 연구하는 것도 일반적이다.이 경우 S는 교합연과 같은 특이점을 가질 수 있다.그러한 표면은 보통 특이성 이론에서 연구된다.다른 약화된 형태의 규칙적인 표면은 컴퓨터 지원 설계에서 발생하는데, 여기서 표면은 분리된 조각으로 분해되며,^{[citation needed]} 국소 매개변수화의 파생물은 경계를 따라 연속되지도 못합니다.

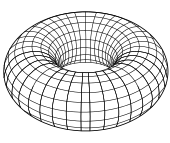
간단한 예.정면의 간단한 예는 2-구 {(x, y², z²) x + y + z² = 1)로 제시되며, 이 표면은 6개의 Monge 패치(상기 3가지 유형 각각 2개)로 커버될 수 있으며, 이때 h(u, v) = ± (1² - u - v²)^1/2이다.또한 입체 투영을 사용하여 두 가지 로컬 매개 변수로 커버할 수 있습니다.집합 {(x, y, z) : (x² + y²)^1/2 - r)² + z² = R²}은 반지름이 r 및 R인 회전 토러스입니다.이것은 정규 표면입니다. 로컬 매개 변수를 형식에 제공할 수 있습니다.

$({displaystyle f(s,t)=big (})(R\cos s+r)\cos t,(R\cos s+r)\sin t,R\sin s(big)}).}$

두 시트 {(x, y, z): z² = 1 + x² + y²} 위의 쌍곡선은 정칙 표면이며, h(u, v) = ±(1 + u² + v²)^1/2인 두 개의 Monge 패치로 덮을 수 있습니다.헬리코이드는 최소 표면 이론에서 나타난다.단일 국소 매개변수화 f(u, v) = (u sin v, u cos v, v)로 커버됩니다.

탄젠트 벡터 및 법선 벡터

S를 δ의³ 정면으로 하고 p를 S의 성분으로 한다.위의 정의 중 하나를 사용하여 δ의³³ 특정 벡터는 p에서 S에 대한 탄젠트로, δ의 특정 벡터는 p에서 S에 대한 직교로 선택할 수 있습니다.

정의에 사용되는 개체	δ의3 벡터 X는...의 경우 p에서 S에 접선한다.	δ의3 벡터 n은 p에서의 S에 대하여 ...의 경우 정규이다.
로컬 파라미터화	... 임의의 로컬 파라미터화 f : V → S with p ∈ f(V)에서 X는${\displaystyle \frac{\mathrm{}}{}}$f${\displaystyle \frac{\mathrm{}}{}{}_{}\frac{}{}{}_{{}^{}}}$f -${\displaystyle {{}^{}}_{}}$${\displaystyle {1^{}}_{}}$ (${\displaystyle p_{}}$ $)\$ \$frac$ {\fac f${\displaystyle {{\}}^{}}_{}}$$${\$big$ ${\displaystyle \frac{\mathrm{}}{}{}_{}\frac{}{}{}_{{}^{}}}\{{\displaystyle \frac{\mathrm{}}{}}$$f^$ {-$1}(p$$textstyle$1${\displaystyle {{}^{}}_{}}$(\textstyle )의 선형 조합입니다$.$$(p)}}:$	...그것은 p에서 S에 대한 모든 접선 벡터에 직교한다.
Monge 패치	...범위에 p가 포함되는 임의의 Monge 패치(u, v) † (u, v, h(u, v)에 대해서는, 다음과 같이 합니다. ${\displaystyle X^{1}{\frac h}{\frac u}+X^{2}{\frac {\frac h}{\frac v}}-X^{3}=0,}$ (p1, p2) 지점에서 평가된 부분 도함수를 사용하여.유사한 정의는 다른 두 가지 형태의 Monge 패치의 경우에도 적용된다.	...어떤 몽주 패치에)↦(u, v, h(u, v)(u, v)의 범위(.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{p, n배수로를 포함한다.디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}∂h/∂u, ∂h/∂v, −1)때(p1, p2)에서 평가된다.유사한 정의는 다른 두 가지 형태의 Monge 패치의 경우에도 적용된다.
암묵적 함수	...영역이 p를 포함하는 임의의 로컬 정의 함수 F에 대해 X는 θF(p)와 직교한다.	도메인이 p를 포함하는 로컬 정의 함수 F의 경우 n은 "F(p)"의 배수입니다.

p의 S에 대한 모든 접선 벡터로 정의되는 p의 S에 대한 접선 공간 또는 접선 평면이 δ의³ 2차원 선형 부분 공간임을 알 수 있습니다. 종종 TS로 표시됩니다_p.p의 S에 대한 법선 공간은 p의 S에 대한 모든 법선 벡터로 정의되며, 탄젠트_p 공간 TS에 직교하는 δ의³ 1차원 선형 부분 공간입니다.따라서 S의 각 점 p에는 단위길이의 2개의 법선 벡터(단위법선 벡터)가 있다.p에서의 단위 정규 벡터는 공식을 통해 로컬 파라미터화, Monge 패치 또는 로컬 정의 함수의 관점에서 제공될 수 있습니다.

$\displaystyle.{\frac {\frac f}{\frac f}{\frac v}}\times {\frac f}{\frac f}{\frac v}{\frac v}{\f}{\big }}{f^{-1}(p)\q}\ad 왼쪽.{{\frac {\frac {\partial h}{\partial v},-1{\big}}}{sqrt {1+{\frac {\partial h}{\partial u}{\big}{\frac}{\partial u}{\partial u}{\frac}{\frac}{\partial v}}{\frac}{\partial v}{\partial v}}{\partial v}}{\frac}}}{\partial v}{\$

이전 정의와 동일한 표기를 따릅니다.

접선 벡터의 "내적" 정의를 메모하는 것도 유용합니다. 이것은 매끄러운 다양체의 설정에 대한 규칙적인 표면 이론의 일반화의 전형적인 예입니다.이것은 탄젠트 공간을 δ의³ 선형 부분 공간이 아닌 추상적인 2차원 실제 벡터 공간으로 정의합니다.이 정의에서는 p에서의 S에 대한 탄젠트 벡터는 2개의 숫자¹ X와² X의 각 국소 매개변수 f : V → S에 대한 할당이며, 다른 국소 매개변수 f f : V → S에 대해 p ∈ f(V) (및 대응하는 숫자 X)¹를 갖는 할당이라고 한다.

$(\displaystyle\begin{pmatrix}X^{1}\X^{2}\end{pmatrix}=A_{f'(p)}{\begin{pmatrix}(X')^{1}\\(X')^{2}\end{pmatrix}}.$

여기서_{f ′(p)} A는 fθ(p) 지점에서 평가된 매핑 ⁻¹ fθ fθ의 야코비안 행렬이다.p에서 S에 대한 접선 벡터의 집합은 자연스럽게 2차원 벡터 공간의 구조를 가지고 있다.이 의미의 탄젠트 벡터는 다음 벡터를 고려함으로써 이전 의미의 탄젠트 벡터에 대응한다.

${\displaystyle X^{1}{\frac {\partial f}{\partial u}}+X^{2}{\frac {\partial v}}.}$

X와³ X의¹² 야코비안 조건은 사슬 규칙에 의해 이 벡터가 f에 의존하지 않음을 보증한다.

표면의 매끄러운 함수를 위해 벡터 필드(즉, 탄젠트 벡터 필드)는 1차 연산자 또는 파생물로 중요한 해석이 있습니다.$(\displaystyle$ S$)$를 정규 표면, U$(\displaystyle$ U$)$를 평면의 열린 부분 집합, f:${\displaystyle U}$ ${\displaystyle \to }$(\$displaystyle$ f$:$$좌표$ 차트 U$$$\오른쪽 화살표$ S$.$$V{\displaystyle }$ ${\displaystyle =f}$ ( ${\displaystyle U}$) { $displaystyle$ V $= f$ ($U$ ) $c{\displaystyle {}^{}}$$$（ $U$ \$displaystyle$ C^ { \ $infty$$$} ( $U$)공간 C c ( U )는 C ${\displaystyle {}^{}}$ (${\displaystyle V}$){ $displaystyle$ C^ { \ $infty$} ( V )로 식별할 수 $있습니다.$ $마찬가지$로 U $styledisplaystyle$ F$$$ident{\displaystyle }$ ident fields fields fields fields fields fields$$ident$$ 。ariables u 및 v, 벡터 필드는 X ${\displaystyle =}$ ${\displaystyle a{\mathrm{}}_u}$+ $b$ ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle v_{}}${ $displaystyle$ X $= a$ \ $partial$_ { $u$} +$b$ \$partial$_ { v$$}$형식$을 가지며, a 및 b의 스무스 함수는 다음과 같습니다.X$(디스플레이 스타일$ X$)$가 벡터 $필드$이고 g$(디스플레이 스타일$ g$)$가 매끄러운 함수인 $경우{\displaystyle }$ X$(디스플레이$ 스타일 Xg$$$)$도 매끄러운 함수입니다.1차 미분 $연산자{\displaystyle }$X({$display$X})는$$ 파생된 것으로, 라이프니츠 $규칙{\displaystyle }$ X${\displaystyle (g}$ h${\displaystyle )}$ $=$ (${\displaystyle X}$ g${\displaystyle )h}$ +${\displaystyle g}$ (${\displaystyle X}$h${\displaystyle }$)$$. {$display style$X($gh$)=($Xg)h+g(Xh)$를 만족합니다.$}$^[19]

벡터 필드 X 및 Y의 경우${\displaystyle }$연산자 [${\displaystyle X,}$ ${\displaystyle Y]}$ ${\displaystyle =}$ ${\displaystyle X}$Y - ${\displaystyle Y}$ ${\displaystyle X}${$style [X,$Y] =$XY-YX}$가 벡터 필드에 대응하는 유도체인지 확인하는 것은 간단합니다.이것은 Lie 브래킷 $]({displaystyle$[${\displaystyle X,}$ ${\displaystyle Y}$$])$이라고 합니다.${\displaystyle \mathrm{이것}}$은 스큐 [X, Y$=$ - [ ${\displaystyle Y,}$ X$$]({displaystyle [$X,$ Y]={$displaystyle [X$, Y], X$])$이며 Jacobi ID를 충족합니다.

${\displaystyle [[X,Y],Z]+[Y,Z],X]+[Z,X]=0.}$

요약하면 U$${$displaystyle$ U$}$ $또는$ V {$displaystyle$ V$}$의 벡터 필드는 Lie ^[20]괄호 아래에 Lie 대수를 형성합니다.

첫 번째 및 두 번째 기본 형식, 형상 연산자 및 곡률

S를 δ의³ 정표면이라고 하자. 국소 파라미터화 f : V → S와 단위 법선 벡터장 n ~ f(V)가 주어졌을 때, 다음 객체를 V 위의 실수값 함수 또는 행렬값 함수로 정의한다.첫 번째 기본 형태는 f에만 의존하며 n에는 의존하지 않습니다.네 번째 열에는 f에 대해 다른 국소 매개변수화 선택에서 발생하는 함수 E ,, F ,, G ,, L , 등을 관련지어 f에 의존하는 방법을 기록한다.여기서 A는 f f f ′의 ^–1 야코비아 행렬을 나타낸다.네 번째 열의 공식을 확립할 때 중요한 관계는 다음과 같습니다.

${\displaystyle\frac{pmatrix}{\frac{pmatrix}}\frac{pmatrix}=A{\begin{pmatrix}{\frac{partial f}{\partial u}}\{\frac{partial v}}\end{pmatrix}}$

체인의 법칙에 따라 다음과 같습니다.

용어.	표기법	정의.	로컬 파라미터화에의 의존성
제1기초형식	E	$(*displaystyle E=cdfrac {\cdot u}\cdot {\cdfrac f} {\cdfac u})$	$(\displaystyle\begin{pmatrix}E&F'\F'&G'\end{pmatrix}=A{\begin{pmatrix}E&F&G\end{pmatrix}A^{T}}$
	F	${\displaystyle F=cdfrac {\cdot u}\cdot {\cdfrac f}$
	G	${\displaystyle G=cdfrac {\cdot v}\cdot {\cdfrac frac {\cdf}$
제2기초형식	L	${\displaystyle L=cdfrac {\cdot u^{2}f} {\cdot n}$	$디스플레이 스타일L'&M'\M'&N'\end{pmatrix}=A{\begin{pmatrix}L&M\M&N\end{pmatrix}}A^{T}}$
	M	${\displaystyle M=syslogfrac {\syslog u\syslog v}\cdot n}$
	N	${\displaystyle N=cdfrac {\display v^{2}f} {\cdot n}$
형상 연산자[21]	P	${\displaystyle P=begin{pmatrix} L&M\M&N\end{pmatrix}{\begin{pmatrix}E&F\\F&G\end{pmatrix}^{-1}$	${\displaystyle P'=APA^{-1}}$
가우스 곡률	K	${\displaystyle K=snfrac {LN-M^{2}}{EG-F^{2}}}}$	${\displaystyle K'=K}$
평균 곡률	H	${\displaystyle H=gl-2FM+EN}{2(EG-F^{2}}}}$	${\displaystyle H'=H}$
주요 곡선	${\displaystyle\kappa_{\pm}}$	${\displaystyle H\pm {H^{2}-K}}$	$\displaystyle \kappa _{\pm}'=\kappa _{\pm}}$

형상연산을 정의하는 행렬을 사용한 직접 계산에 의해 가우스 곡률이 형상연산자의 결정인자, 평균 곡률이 형상연산자의 트레이스, 주 곡률이 형상연산자의 고유값임을 확인할 수 있다. 게다가 가우스 곡률은 주 cu의 곱이다.평균 곡면성이 합계가 됩니다.이러한 관측치는 이러한 개체의 정의로도 공식화할 수 있습니다.이와 같은 관측치를 통해 유사한 행렬의 행렬식, 추적 및 고유값이 동일하므로 네 번째 열의 마지막 세 행이 이전 행 바로 뒤에 오는 것도 확인할 수 있습니다.E, G 및 EG - F는² 모두 반드시 양수라는 점에 유의해야 합니다.이렇게 하면 형상 연산자의 정의에서 행렬 역행렬이 잘 정의되고 주요 곡선이 실수입니다.

또한 단위 정규 벡터 필드의 선택을 부정하면 두 번째 기본 형태인 형상 연산자, 평균 곡률 및 주요 곡률은 부정되지만 가우스 곡률은 변경되지 않습니다.요약하면, 규칙 표면 S가 주어졌을 때, S의 가우스 곡률은 S의 실수치 함수로 간주될 수 있음을 알 수 있다. S의 모든 단위 정규 벡터장 선택과 관련하여, 2개의 주요 곡률과 평균 곡률도 S의 실수치 함수이다.

기하학적으로 제1 및 제2의 기본형식은 f(u, v)가 V 내에서 이동함에 따라 f(u, v)가 어떻게³ 움직이는지 정보를 제공하는 것으로 볼 수 있다.특히 제1의 기본형식은 f가 얼마나 빨리 움직이는지를 부호화하고, 제2의 기본형식은 f의 움직임이 법선 벡터 n의 방향으로 향하는 정도를 부호화한다.즉, p점에서의 두 번째 기본 형태는 S에서 p점에서의 탄젠트 평면으로의 직교 투영 길이를 부호화하며, 특히 이 길이에 가장 가까운 2차 함수를 제공한다.이 생각은 공식에 의해 정확하게 만들어질 수 있다.

${\displaystyle {{begin{aligned}\lim _{(h,k)\to (0,0)}{\frac {\big }f(u+h,v+k)-f(u,v){\big }-{2}-{\big (}Eh^2}+2Fhk+Gk^{2}{\big}}}{h^{2}+k^{2}}}&=0\lim _{(h,k)\to (0,0)}{\frac {\big (}f(u+h,v+k)-f(u,v){\big}{\frac {1}{\big (}Lh^{2}+2Mh+k}{k}{k}{k}{k}{\big (\big (\big (0)})})})}}}&=0,\end {aligned}}$

기본 형태와 테일러의 2차원 정리의 정의에서 직접 나온 것이다.주요 곡선은 다음과 같은 방법으로 볼 수 있다.S의 특정 지점 p에서 S에 대한 직교 선을 포함하는 모든 평면의 모음을 고려합니다.이러한 각 평면은 S와의 교차곡선을 가지며, 이는 평면 자체의 평면곡선으로 간주할 수 있다.고려 중인 평면이 정규선 주위를 회전하기 때문에 p에서 두 개의 주요 곡선은 p에서 이 평면 곡선의 가능한 최대 및 최소 곡률 값이다.

다음은 Monge 패치 f(u, v) =(u, v, h(u, v))에 대한 상기 수량의 계산을 요약한 것입니다.여기서_u h와_v h는 h의 두 부분 도함수를 나타내며, 두 번째 부분 도함수에 대해서도 유사한 표기법을 사용한다.두 번째 기본 형태와 모든 후속 수량은 주어진 단위 법선 벡터장 선택과 관련하여 계산됩니다.

양	공식
단위 법선 벡터장	${\displaystyle n=subfrac {(-h_u},-h_{v},1}}{\subrt {1+h_{u}^2}+h_{v}^2}}}$
제1기초형식	$디스플레이 스타일(디스플레이 스타일\begin{pmatrix\) E&)F\\F&G\end{pmatrix}=begin{pmatrix}1+h_{u}^{2}&h_{v}\h_{u}h_{v}&1+h_{2}\end{pmatrix}}$
제2기초형식	${\displaystyle {begin{pmatrix} L&M\end{pmatrix}=sqrt {1+h_{u}^{2}+h_{v}^{2}}}{\sq {pmatrix}h_{u}&h_h_u}{pmatrix}}$
형상 연산자	${{displaystyle P=hpfrac {1}{2}^{2}+h_{v}^{2}^3/2}}}{\time {pmatrix}h_{u}(1+h_{v}^2}-h_{u}-{u}h_{u}-{h}^{h_u2}-{{h}-{h}-{h}-{h}-{h}-{h}-{h}-{u}-{h}-{h}-{h}-{h}-{h}-{u}-{u}-{$
가우스 곡률	${{displaystyle K=black {h_{uu}h_{v}-h_{uv}^2}{(1+h_{u}^2}+h_{v}^2}^{2}}}}$
평균 곡률	$({displaystyle H=hcfrac {(1+h_{v}^2})h_{uu}-2h_{u}h_{uv}+(1+h_{u}^{2})h_{v}{(1+h_{u}^2}+h_{v}^{2}}}}{{(3/2})}})$

크리스토펠 기호, 가우스-코다치 방정식 및 이론마 에그리움

S를 δ의³ 정면으로 하자.Christofel 기호는 각 국소 매개변수 f : V → S에 다음과 같이 정의된^[22] 8개의 함수를 할당합니다.

${\displaystyle {begin{pmatrix}\Gamma _{11}^{1}&\Gamma _{22}^{1}&\Gamma _{11}^2}&\Gamma _{12}^{2}&\Gamma _{21}^{1}&\Gamma_{12}^{1}_Gamma_{12}F\\F&.G\end{pmatrix}}^{)}{\begin{pmatrix}{\frac{1}{2}}{\frac{\partial E}{마\partial}}&{\frac{1}{2}}{\frac{\partial E}{v\partial}}&{\frac{1}{2}}{\frac{\partial E}{v\partial}}&{\frac{F\partial}{v\partial}}-{\frac{1}{2}}{\frac{G\partial}{마\partial}}\\{\frac{F\partial}{마\partial}}-{\frac{1}{2}}{\frac{\partial E}{v\partial}}&.앰프,{\frac{1}{2}}{\frac {\partial u}{\frac {1}{2}}{\frac {1}{\partial u}}{\frac {1}{\frac {{partial G}{\partial v}}\end{pmatrix}.}$

또한 다음 공식으로 정의할 수 있습니다. 여기서 n은 f(V)에 따른 단위 법선 벡터장이고 L, M, N은 두 번째 기본 형식의 해당 성분입니다.

${\displaystyle{\begin{정렬}{\frac{\partial ^{2}f}{\partial u^{2}}}&=\Gamma _{11}^{1}{\frac{\partial f}{마\partial}}+\Gamma _{11}^{2}{\frac{\partial f}{v\partial}}+Ln\\{\frac{\partial ^{2}f}{u\partial v\partial}}&=\Gamma _{12}^{1}{\frac{\partial f}{마\partial}}+\Gamma _{12}^{2}{\frac{\partial f}{v\partial}}+Mn\\{\frac{\partial. ^{2}f}{)partial v^{2}}&=Gamma _{22}^{1}{\frac {\frac f}{\gamma u}+{22}^2}{\frac {\frac f}{\gamma v}}+N.\end { aligned}}$

이 정의의 핵심은 f/∂u, f/vv 및 n이 각 점에서 each의³ 기초를 형성한다는 것이다. 이 세 개의 방정식은 각각 고유하게 크리스토펠 기호를 f의 두 번째 부분 도함수의 좌표로 지정한다.단위 법선의 선택은 Christofel 기호에는 영향을 주지 않습니다. 왜냐하면 n이 부정과 교환되면 두 번째 기본 형식의 성분도 부정되므로 Ln, Mn, Nn의 부호는 변경되지 않습니다.

두 번째 정의는 국지적 매개 변수화의 맥락에서 크리스토펠 기호가 기하학적으로 자연스럽다는 것을 보여준다.첫 번째 정의의 공식은 덜 자연스러워 보이지만, 크리스토펠 기호가 두 번째 정의에서 바로 드러나지 않는 첫 번째 기본 형태에서 계산될 수 있다는 것을 보여주는 것이 중요합니다.정의의 동등성은 첫 번째 정의를 두 번째 정의로 직접 대체하고 E, F, G의 정의를 사용하여 확인할 수 있다.

코다치 방정식은 다음과 같이 주장한다^[23].

${\displaystyle {\frac L}{\partial v}-{\frac {\partial u}=L\Gamma _{12}^{1}+M(\Gamma _{12}^2}-{11}^{1}-N\Gamma _{2}^{{}{fr}-{fr}\end { aligned}}$

이러한 방정식은 위에 주어진 크리스토펠 기호의 두 번째 정의에서 직접 도출될 수 있습니다. 예를 들어, 첫 번째 코다치 방정식은 v에 대한 첫 번째 방정식, u에 대한 두 번째 방정식, 두 개를 빼고 n으로 도트곱을 취함으로써 얻을 수 있습니다.가우스 방정식은 이라고 주장한다^[24].

$디스플레이 스타일KE&=gamfrac {\gamma _{11}^{2}{\frac {\gamma v}-{\frac {\gamma _{21}^{2}\Gamma _{11}^{1}+\Gamma _{22}^{2}^{}^{{}^2}^2}_{\Gamma}_{{{{{{}_}_}_}_{{{{{{{{}}}}}_}}_Framma}^2}_}_}_}KF&, ={\frac{\partial \Gamma_{12}^{2}}{v\partial}}-{\frac{\partial \Gamma_{22}^{2}}{마\partial}}+\Gamma _{21}^{2}\Gamma _{12}^{1}-\Gamma _{11}^{2}\Gamma _{22}^{1}\\KG&, ={\frac{\partial \Gamma_{22}^{1}}{마\partial}}-{\frac{\partial \Gamma_{12}^{1}}{v\partial}}+\Gamma _{11}^{1}\Gamma _{22}^{1}+\Gamma _{12}^{1}\Gamma _{22}^{2}-\Gamma_{.21}^{1}\감마 _{12}^{1}-\Gamma _{22}^{1}\Gamma _{12}^2}\end{aligned}}$

이것들은 코다치 방정식과 비슷하게 도출될 수 있는데, 하나는 n을 갖는 도트 곱 대신 와인가튼 방정식을 사용한다.이것들은 세 개의 독립된 방정식으로 쓰여져 있지만, 첫 번째 기본 형태에 대한 크리스토펠 기호의 정의를 대입하면 동일하다.결과식을 쓰는 방법에는 여러 가지가 있는데, 그 중 하나는 1852년에 브리오스키가 ^[25][26]행렬식을 능숙하게 사용하여 도출한 것입니다.

${\displaystyle K={\frac{1}{(EG-F^{2})^{2}}}\det{\begin{pmatrix}-{1\over 2}{\frac{\partial ^{2}E}{\partial v^{2}}}+{\frac{\partial ^{2}F}{u\partial v\partial}}-{1\over 2}{\frac{\partial ^{2}G}{\partial u^{2}}}&{1\over 2}{\frac{\partial E}{마\partial}}&{\frac{F\partial}{마\partial}}-{1\over 2}{\frac{\partial E}{v\partial}}\\{\f.rac{\paRtial F}{v\partial}}-{1\over 2}{\frac{G\partial}{마\partial}}&.E&, F\\{1\over 2}{\frac{G\partial}{v\partial}}&.F&, G\end{pmatrix}}-{\frac{1}{(EG-F^{2})^{2}}}\det{\begin{pmatrix}0&,{1\over 2}{\frac{\partial E}{v\partial}}&{1\over 2}{\frac{G\partial}{마\partial}}\\{1\over 2}{\frac{\partial E}{v\partial}}&.E&, F\\{1\over 2}{\frac{\partial G.}{\partial u}}&F&G\end{pmatrix}}.}$

크리스토펠 기호가 첫 번째 기본 형태에 의해 정의된 것으로 간주될 때, 가우스와 코다치 방정식은 첫 번째와 두 번째 기본 형태 사이의 특정한 제약을 나타냅니다.가우스 방정식은 가우스 곡률을 다른 정보 없이 첫 번째 기본 형태에서 직접 계산할 수 있음을 보여주므로 특히 주목할 만하다. 이는 LN - M이² 개별 성분 L, M, N이 불가능하더라도 실제로 E, F, G의 함수로 작성될 수 있음을 의미한다.이것은 이론 이론으로 알려져 있고, 칼 프리드리히 가우스의 주요한 발견이었다.이것은 특히 S의 가우스 곡률의 기하학적 정의를 최대 및 최소 원 반지름에 의해 정의된 것으로 상기할 때 두드러진다; 그것들은 근본적으로 S가 δ³ 내에서 구부러지는 방법의 기하학적 구조에 의해 정의되는 것처럼 보인다.그럼에도 불구하고, 이 정리는 S의 "내적" 기하학에서 S의 곱이 결정될 수 있다는 것을 보여주며, 이는 S를 따르는 곡선의 길이와 교차점에 형성된 각도와 관련이 있다.Marcel ^[27]Berger가 말했듯이:

이 정리는 이해하기 어렵다.[...] 이것은 다른 수학자에 의해 발견되기까지 수십 년을 더 기다려야 할 정리이다. 왜냐하면, 많은 지적 역사와는 달리, 그것은 절대 공중에 있지 않기 때문이다.[...] 오늘날 우리가 아는 한 이론의 간단한 기하학적 증거는 없다.

가우스-코다치 방정식은 엘리 카르탕에 ^[28]의해 연결 형식의 언어로 간결하게 표현되고 도출될 수도 있다.− h2)R및 두Codazzi 방정식 ∇1 h12 = ∇2 h11과∇1 h22)∇2 h12로 쓸 수 있텐서 미적분학의 언어, 자연 지표와 텐서 결합 상품에 대한 연결 사용을 하면서 그 가우스 방정식 H2으로 하고, 복잡한 표현 크리스토펠 기호와 첫번째 기본 형식과 관련 완전히 흡수되면서 작성할 수 있다.그 def에공변 텐서 도함수 δh와 스칼라 곡률 R의 추론.피에르 보네는 가우스-코다치 방정식을 만족시키는 두 개의 2차 형식이 항상 ^[29]국소적으로 내장된 표면을 고유하게 결정한다는 것을 증명했다.이러한 이유로, 가우스-코다치 방정식은 종종 내장 표면의 기본 방정식이라고 불리며, 내적 및 외적 곡선이 어디에서 오는지를 정확하게 식별합니다.그것들은 보다 일반적인 리만 다양체에 포함된 표면에 대한 일반화를 인정한다.

등각선

$정표면{\displaystyle }$S의 $열린{\displaystyle }$ 집합$$$U$와$V$의 차동형상$δ({$$displaystyle$$\$$varphi})$는 메트릭을 보존하면 등각이라고 한다(즉, 제1의 기본형상$).$^[30][31][32]따라서 U$(\displaystyle$ U$)$의 모든 점$$p(\$displaystyle$ p$)$와 p$(\displaystyle$ p$)$의 접선 $벡터{\displaystyle {}_{}}$ ${\displaystyle {w1\mathrm{}}_{}}$ $(\$},\,$w_{2$})에$$ 대해 동등성이 존재합니다.

$\displaystyle E(p)w_{1}\cdot w_{1}+2F(p)w_{1}\cdot w_{2}+G(p)w_{2}=E(\varphi(p)\varphi ^{\prime}(w_{1}\cdot ^{p})\cdot ph}$

첫 번째 기본 형태에서 유래한 내부 제품의 관점에서, 이것은 다음과 같이 다시 쓰여질 수 있습니다.

${\displaystyle (}$ ${\displaystyle {}_{}{1\mathrm{}}_{}}$ , w ${\displaystyle 2_{}}$ ) p${\displaystyle {}_{}}$ (${\displaystyle {}^{}{}_{}{1\mathrm{}}_{}}$) ,${\displaystyle {}^{}}$w ${\displaystyle {}_{}}$)${\displaystyle {\phi }_{}}$ p ${\displaystyle {（\mathrm{}}^{}}$ ${\displaystyle p_{}}$ \ $displaystyle$($w$ {$1$ , $w$_ {$2$ ) _ { $p$} = ( \ $varphi$^ { \ prime } ( $w$_ { 1$$} ) 、 \ $varphi$^ { \ $phi$^ { \ prime } ( w$$_ { 2 } ( w _ { 2${\displaystyle {}_{}{}_{}}$} ) } ) _$phi )$} （ w _ $phi$ )

한편 매개변수화된 곡선의 길이${\displaystyle }\theta {\displaystyle }$ (${\displaystyle t}$ ) ${\displaystyle =}$ (${\displaystyle x}$ (${\displaystyle t}$) ,${\displaystyle y}$ (${\displaystyle t}$ )$${ $displaystyle$ \ $displaystyle$( t ) = ($x$ ($t$ ) ,$y$ ($t$ )}는$$ 다음과 같이 계산할 수 있다.

${\displaystyle L(\gamma)=\int _{a}^{b}{\cdot {x}}\cdot {x}+2F{\dot {x}}\cdot {y}+G{\dot {y}}\cdot {y}}\cdot {dt}{dt}$

곡선이 $\style$ U$\backslash$$display$ U일 경우 변수 변경 규칙은 다음과 같습니다.

$\displaystyle L(\varphi \displays \gamma)= L(\gamma).}$

$반대$로 ${\$ { $displaystyle$\$varphi }$가 곡선으로 분류된 모든 파라미터의 길이를 유지하는 경우 ${\$ { \ $displaystyle$\ $varphi }$는 등척도가 됩니다.$실제로{\displaystyle }$ ${\$ { $display$style \ $gamma$의 적절한 선택지에 대해 접선 $벡터{\displaystyle \stackrel{}{}}$ x ${\$ {$displaystyle${ $x$$$} 및$$ $y{\displaystyle \stackrel{}{}}$ ${\$ {$displaystyle${ y$}$는 임의의 접선 $벡터{\displaystyle {}_{}}$ ${\displaystyle {w\mathrm{}}_{}}$ 1$${ $displaystyle w_{1}$ 및$$ $w{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}${ $displaystyle w_{2$를 제공합니다.모든$$접선 $벡터{\displaystyle {}_{}}$ $w1$(\$displaystyle$ $w\_$${$1$})$과 w2(\$displaystyle$ w_$$${2})$ 및 $w{\displaystyle {}^{}}$$displaystyle$\varphi$^{\$$prime$}(${$$1})$ 및$$ w$(\displaystyle \$${\displaystyle {}^{}}$ $^{1$})에 대해 동등성이 유지되어야 합니다$.$${\displaystyle {)}_{}=}$ ( ${\displaystyle {w\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$, ${\displaystyle {w\mathrm{}}_{}{}_{}}$1 )$$ \ $displaystyle$( \ $varphi ^$ { \ $prime$} ( $w$_ { } ) , \ $varphi$^ { \ prime } ($w$_ { } ) _ { \ $varphi$ ( p ) = ($w _${ 1 ,$w$ _ { 1$$}$$_ {$$p $\}$^[33] } } } } } 。

등각계의 간단한 예는 일반 $표면{\displaystyle {}_{}}$ $($ S_${1$}) $및{\displaystyle {}_{}}$ $($ S_${2})$의 개방형 $세트{\displaystyle }$U({$디스플레이 스타일$ U$})$의 두 가지 $매개변수{\displaystyle {}_{}}$ $({$ 스타일 $f_{$1$$})과 $({$ style$$f_${$$2$}})에$$ 의해 제공됩니다. $If{\displaystyle {}_{}}$ ${\displaystyle {E1\mathrm{}}_{}}$ $= E_2$(디스플레이 $스타일 S_2).$, ${\displaystyle {F1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {F2\mathrm{}}_{}}$({$style$ F_${1$} =$F_{2}}$ $및$ ${\displaystyle {G1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {G2\mathrm{}}_{}}$({$displaystyle G_{$1} $=$ G_${2}$ )$$then 、 ${\displaystyle {}_{}}$ ${\displaystyle {}_{}^{}}$1${\displaystyle {}_{}^{}}$- ${\displaystyle 1_{}^{}}$ $(\displaystyle$ \$varphi = f_{2}^{-1$})은 ${\displaystyle \mathrm{fmetry}}$입니다${\displaystyle .}$

실린더와 평면은 국소 등각선이지만 위상적인 ^[35]이유로 등각선까지 확장할 수 없는 표면의 예를 제시한다.또 하나의 예로서 카테노이드와 헬리코이드는 국소등축이다.^[36]

공변 도함수

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2020년 8월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

S 위의 접선 벡터장 X는 S의 각 p에 p의 접선 벡터_p X~S를 할당한다.위에서 주어진 탄젠트 벡터의 "정확한" 정의에 따라, 접선 벡터장 X는 각 로컬 매개변수 f : V → S에 다음과 같이 두 개의 실값¹ 함수² X와 X를 할당합니다.

${\displaystyle X_{p}=X^{1}{\big (}f^{-1)(p){\big u}{\big }_{f^{-1}(p)}+X^{2}{\big (}f^{-1(p){\big}frac}{\frac}{\big} f}$

S의 각 p에 대해어떤 사람은 함수¹ X와² X가 매끄럽다면 f ^[37]중 어떤 것을 선택해도 X는 매끄럽다고 말한다.상기 탄젠트 벡터의 다른 정의에 따르면, S의 각 p에 대해 X(p)가 탄젠트 공간_p TS θ θ에³ 포함되도록 S 위의 탄젠트 벡터장 X를 지도 X : S → θ로³ 간주할 수도 있다.평활 다지관의 보다 일반적인 상황에서 흔히 볼 수 있듯이, 접선 벡터장은 S 위의 평활함수 공간에서 특정 미분 연산자로 정의될 수 있다.

Tullio Levi-Civita와 Gregorio Ricci-Curbastro의 공변 도함수("접선 도함수")는 매끄러운 접선 벡터장을 미분하는 수단을 제공한다.p에서의 접선 벡터장 X와 접선 벡터 Y~S가 주어졌을 때, 공변 도함수 _YθX는 p에서의 S에 대한 특정 접선 벡터이다.따라서 X와 Y가 모두 접선 벡터장이면 _YδX도 접선 벡터장으로 볼 수 있으며, 반복적으로 X, Y, Z가 접선 벡터장이면 또 다른 접선 벡터장이 되는 _ZYδX를 계산할 수 있다.공변 미분을 정의하는 방법에는 몇 가지가 있습니다. 첫 번째 방법은 Christofel 기호와 탄젠트 벡터의 "내적" 정의를 사용하고, 두 번째 방법은 보다 명백하게 기하학적입니다.

접선 벡터 필드 X와 p에서 접선 벡터 Y에서 S로 주어진 경우,_Y δX를 로컬 파라미터레이션 f : V → S에 할당하는 p에 대한 접선 벡터라고 정의합니다.

$(\displaystyle _{Y}X)^{k}=D_{(Y^{1},Y^{2})}X^{k}{\Big}_{f^{-1}(p)+\sum_{i=1}^{2}\sum_{{j1}^{big}{\gami}_{k}_gami}_{{k}_{{{k}_}_}_{{{{{k}}}}}}Y^{i},\qquad(k=1,2)}$

여기서_{(Y¹, Y²)} D는 방향 ^[38]도함수입니다.이것은 종종 아인슈타인 표기법을 사용하고 함수의 평가 위치를 암묵적으로 이해하면서 덜 번거로운 형태(_YδX)^k = _Yδ(X ^k) + YδX로 ^ik
_ij ^j 축약된다.이는 리만 기하학에서 리만 미터법에서 연결을 얻기 위한 표준 규정을 따릅니다.벡터는 기본적 사실이다.

${\displaystyle(\nabla_{Y}X)^{1}{\frac {\partial u}+(\nabla_{Y}X)^2}{\frac {\partial v}}}$

δ에서는³ 로컬 파라미터화 f의 선택과는 무관하지만 확인은 다소 번거롭습니다.

또한 Christofel 기호나 ^[39][40][41]국소 매개변수를 사용하지 않는 다음과 같은 기하학적 접근법에 의해 공변 미분을 정의할 수 있다.X를 함수 S → δ로³ 보는 S 위의 벡터장이라고 하자. 어떤 곡선 c : (a, b) → S일 때, X δ c : (a, b) → δ를 고려할³ 수 있다. 유클리드 공간 사이의 지도로서, 이것은 입력값에서 원소(xθ)를 얻을 수 있다.TS에 대한 이_c(t) 벡터의 직교 투영에 의해 공변 도함수 _{c ′(t)}δX가 정의됩니다.이것은 매우 기하학적으로 깨끗한 정의이지만 결과는 c와 X가 아니라 c'(t)와 X에만 의존함을 보여 줄 필요가 있습니다.이 작은 기술 인수에 로컬 파라미터화를 사용할 수 있습니다.

공변 미분이 S의 첫 번째 기본 형태에만 의존한다는 것은 두 번째 정의에서 즉시 명백하지 않다. 그러나 크리스토펠 기호는 첫 번째 기본 형태에서 직접 정의될 수 있기 때문에 이것은 첫 번째 정의에서 즉시 나타난다.두 정의가 동일한지 확인하는 것은 간단합니다.열쇠는 두번째 부분 유도체 ∂2f에서 날 때ℝ3-valued 함수로 X1∂f/∂u+X2∂f/∂v 관련해서도, 곡선을 따라 그것의 분화 결과;크리스토펠 기호 접선 공간에 직교 도법에는, f의 두번째 파생 상품 상대의 접선 부품 크리스토펠 기호의 형성 때문에를 입력합니다.로.기본 f/csu, f/csv, n.^[38]이것에 대해서는, 상기의 항에서 설명합니다.

세 개의 가우스 방정식의 오른쪽은 공변 미분을 사용하여 표현할 수 있습니다.예를 들어 오른쪽은

$({displaystyle {frac \Gamma _{11}^{2}{\partial v}-{\frac \Gamma _{21}^{2}{\partial u}+{11}^{1}+\Gamma _{22}^{2}_11}_{{{}_2}{\partial u})$

제2좌표로 인식할 수 있다

$\displaystyle \frac {\frac f} {\frac f} {\frac f} {\frac f} {\frac f} {\frac u} - \frac f} {\frac f} {\frac u} {\frac f}$

Christofel 기호에 의한 공변량 미분 정의를 사용하여 직접 검증할 수 있는 기준 θf/θu, θf/θv에 대해 비교한다.리만 기하학의 언어에서, 이 관찰은 또한 가우스 방정식의 오른쪽 변이 리만 메트릭으로 해석될 때 첫 번째 기본 형태의 리치-시비타 연결의 리치 곡률의 다양한 구성요소라고 표현될 수 있다.

예

혁명의 표면

회전면은 xz면에서 z축을 중심으로 곡선을 회전시킴으로써 얻을 수 있다.이러한 표면에는 구체, 원통, 원추체, 토리, 그리고 카티노이드가 포함된다.일반적인 타원체, 쌍곡선, 포물체는 그렇지 않다.곡선이 다음과 같이 모수화된다고 가정합니다.

${\displaystyle x=c_{1}(s), ,,z=c_{2}(s)}$

(a, b) 간격에서 s를 끌어냅니다.c가₁ 0이 아닌 경우, cθ와₂ cθ가 모두 0이 아닌 경우₁, 그리고 c와₂ c가 모두 평활하다면₁, 대응하는 회전 표면은

${\displaystyle S=bigBig \{1}{\cos t,c_{1}(s)\sin t,c_{2}(s){\big}}\cisco s\in (a,b){\text{ and }}\in \mathbbb {R} {R}{\big \c}}$

δ의³ 정규 표면이 됩니다.국소 파라미터화 f : (a, b) × (0, 2µ) → S는 다음과 같다.

$(\displaystyle f(s,t)=cosbig (}c_{1}(s)\sin t,c_{2}(s){\big}).}$

이 매개변수화에 상대적인 기하학적 데이터는 다음과 같습니다.^[42]

양	공식
단위 법선 벡터장	${{displaystyle n=bigfrac {{\big (}-c_{2}(s)\cos t,c_{1}'(s)}}{\bigrt {c_{1}'(s)^{2}+c_{2}(s)}}}}$
제1기초형식	$디스플레이 스타일(디스플레이 스타일\begin{pmatrix\) E&)F\\F&G\end{pmatrix}=(begin{pmatrix}c_{1}'(s)^{2}+c_{2}'(s)^{2}&c_{1}(s)^{2}\end{pmatrix}}}$
제2기초형식	${\displaystyle {\begin{pmatrix}L&M\end{pmatrix}=begin{pmatrix}{\frac {c_{1}'(s)-c_{2}'(s)c_{1}'(s){\beginrt {c_{1}{c}^2}{c}{c}{c}{c}{c}{c}{c}}{c}}{c}{c}}}}{c}{c}{c}}{c}}{c}}}{c}{c}$
주요 곡선	${{displaystyle {c_{1}(s) c_{2}'-c_{2}(s) {\big (s) c_{1}'{2}+c_{2}(s) {2}{3}/2} {\frac} {\text}} {\frac}$
가우스 곡률	${\displaystyle K=bigfrac {c_{2}(s){big (}c_{1}')(s)-c_{2}'(s)c_{1}(s)}{\big}(s)}{\big (c_{1}(s)^{2}'c'\big (s)_{2'}'''c'''''''''''''''''''''''c'c'c')$
평균 곡률	${{displaystyle H=bigfrac {1}{2}{\frac {c_{1}'(s)c_{2}'-c_{2}'(s){\big (}c_{1}'(s)^{2}+c_{2}(s)^{2}}/{2}}^{\}}}{\big}}}$

원래의 곡선이 호 길이(cθ(s₁)² + (cθ₁(s)² = 1)에 의해 매개변수화되는 특별한 경우, cθ(s₁) cθ(s) + cθ₂(s) cθ₂(s) cθ(s₁) = 0)를 구하도록 미분할 수 있다. 가우스 곡률로 치환하면 다음과 같이 단순화된다.

$\displaystyle K=-{\frac {c_{1}'(s)}{c_{1}(s)}}}\qquad {text{and}}\qquad H=c_{1}'(s)-c_{2}'(s)-c_{1}(s)+\frac_{c}{c}{c}{c}{c}{c}}'}'}'}'}'}'s's''s's''''s's'}$

이 공식은 단순하기 때문에 일정한 가우스 ^[43]곡률을 가진 회전 대칭 표면의 클래스를 특히 쉽게 연구할 수 있습니다.c(s) = s라는 대체₂ 사례로 환원함으로써 회전 대칭 최소 표면을 연구할 수 있으며, 그 결과 그러한 표면은 평면 또는 스케일 카테노이드의 ^[44]일부가 된다.

S상의 각 상수-t 곡선은 측지학으로 파라미터화 할 수 있으며, S상의 상수-s 곡선은 cδ(s)가 0인 경우에만₁ 측지학으로 파라미터화 할 수 있다.일반적으로 S 위의 측지학은 Clairaut의 관계에 의해 제어된다.

사각형 표면

정의되어^[45] 있는 4차원 서페이스에 대해 생각해 봅시다.

${\displaystyle {x^2} \over a}+{y^{2} \over b}+{z^{2} \over c}=1.}$

이 표면은 매개 변수화를 허용합니다.

${\displaystyle x=sqrt {a(a-u)(a-v) \over (a-b)(a-c)},,,y=sqrt {b(b-u)(b-v)\over (b-c)},,,,z=sqrt {c(c-u)(c-v)\overrt {c}(a)}$

가우스 곡률 및 평균 곡률은 다음과 같습니다.

${\displaystyle K={abc \over u^{2}v^{2},,,K_{m}=-(u+v){\sqrt {display \over u^{3}v^}}}.}$

괘면

괘면이란 ^[46]E에서의 직선운동에³ 의해 발생할 수 있는 면이다.표면에서 직교하는 직선, 즉 매끄러운 단위 속도 곡선 c(t)를 선택하고, 선 방향의 곡선을 따라 단위 벡터가 될 u(t)를 선택하면 속도 벡터 v = c 및_t u는 다음을 만족한다.

$\ displaystyle u \ cdot v = 0 , , , , \ u \ = 1, , , , , \ v \ = 1 . }$

지표면이 점으로 구성됩니다.

${\displaystyle c(t)+s\cdot u(t)}$

와 t가 다르기 때문에

그러면 만약에

${\displaystyle a=\u_{t}\cdot v,,,\alpha =-{\frac {b}{a^{2}},,,\display =\frac {a^{2}-b^{2}}{a^{2}}},\displaystyle a=\u_u_{t {t}}},\cdot {t}},\frac$

가우스 및 평균 곡률은 다음과 같이 주어진다.

${\displaystyle K=-{\beta ^{2} \over ( ( s - \alpha )^{2} }, , , , K_{m}= - {r [ ( s - \alpha ) } + \ example _ { t } ( s - \ alpha )+ \ alpha _ { tover }}$

규칙 표면의 가우스 곡률은 ^[47]u와_t v가 비례하는 경우에만 사라진다. 이 조건은 접선 벡터 v와 직교 벡터 u를 포함하는 곡선을 따라 곡선을 따라 평면의 포락선인 표면과 같다.^[48] 즉, 곡선을 따라 전개할 수 있는 표면에 대한 조건이다.보다 일반적으로 E의³ 표면은 그 ^[49]지점 근처에서 현상 가능한 경우에만 그 지점 근처에서 소실되는 가우스 곡률을 가진다. (아래에 메트릭의 관점에서 동등한 조건이 제시되어 있다.)

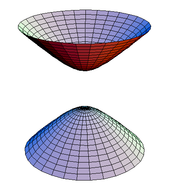
최소 표면

1760년에 라그랑주는 하나의 변수에서 적분을 포함하는 변이의 미적분에 대한 오일러의 결과를 두 ^[50]변수로 확장했다.그는 다음과 같은 문제를 염두에 두고 있었다.

E에³ 닫힌 곡선이 주어졌을 때 곡선이 최소 면적의 경계인 표면을 구한다.

이러한 표면을 최소 표면이라고 합니다.

1776년 장 바티스니에(Jean Batiste Meusnier)는 라그랑주(Lagrange)가 도출한 미분방정식이 표면의 평균 곡률의 소멸과 동등하다는 것을 보여주었다.

표면은 평균 곡률이 사라지는 경우에만 최소입니다.

최소한의 표면은 실제 생활에서 간단한 해석을 가지고 있습니다.곡선 모양의 와이어 프레임을 비누 용액에 담갔다가 조심스럽게 꺼낼 경우 비누 필름이 가정하는 형태입니다.주어진 경계를 가진 최소 표면이 존재하는지에 대한 문제는 19세기 중반 비누막 실험을 수행한 벨기에 물리학자 조셉 플라토 이후 플라토 문제로 불린다.1930년 제시 더글라스와 티보르 라도는 플라토 문제에 대해 긍정적인 대답을 했다.^[51]

카테노이드, 헬리코이드, 스커크 표면 및 엔네퍼 표면과 같은 최소 표면의 많은 명시적 예가 명시적으로 알려져 있다.Oserman(2002년)에 요약된 이 분야에 대한 광범위한 연구가 있었다.특히 Oserman의 결과는 최소 표면이 비평면일 경우 가우스 지도 아래의 이미지는 S로 밀도가² 높다는 것을 보여준다.

일정한 가우스 곡률 표면

표면이 일정한 가우스 곡률을 갖는 경우, 그것은 일정한 ^[52]곡률의 표면이라고 불립니다.

• E의³ 단위 구에는 일정한 가우스 곡률 +1이 있습니다.
• 유클리드 평면과 실린더는 모두 일정한 가우스 곡률 0을 가집니다.
• θ_tt = θ인 회전 표면은 일정한 가우스 곡률 -1을 가집니다.δ(t) = C cosh t, C sinh t, C^{t [53]}e를 취함으로써 특정 경우를 얻을 수 있다.후자의 경우는 트랙트릭스를 중심축 중심으로 회전시켜 생성된 전형적인 의사권이다.1868년 에우제니오 벨트라미는 로바체프스키(1830)와 볼야이(1832)에 의해 독립적으로 발견된 쌍곡면의 기하학과 직접적으로 관련이 있다는 것을 보여주었다.이미 1840년에 F.가우스의 학생인 Minding은 쌍곡면에 ^[54]대한 것과 동일한 의사권에 대한 삼각 공식을 얻었다.이 표면의 본질적 형상은 이제 상부 반평면 또는 단위 디스크의 Poincaré 메트릭의 관점에서 더 잘 이해되었으며, 클라인 모델이나 하이퍼볼로이드 모델과 같은 다른 모델들에 의해 설명되었다. 여기서 q(x, y, z) = -1을 3차원 민코프스키 공간에서 고려함으로써 얻어졌다. = x² + y^{2 [55]}– z².

일정한 곡률의 각 표면에는 대칭의 전이적 Lie 그룹이 있습니다.이 그룹 이론적인 사실은 푸앵카레의 균일화 정리(아래 참조)로 인해 표면의 기하학에서 이러한 특별한 표면이 중심적인 역할을 하기 때문에 더욱 더 큰 영향을 미칩니다.

가우스 곡률이 0인 표면의 다른 예로는 원추체, 접선 현상체 및 보다 일반적으로 현상 가능한 표면이 있습니다.

로컬 메트릭 구조

치수 3 이상의 유클리드 공간에 매설된 모든 표면에 대해 표면상의 곡선의 길이, 두 곡선 사이의 각도 및 표면상의 영역의 면적을 측정할 수 있다.이 구조는 선 요소 및 면적 요소를 통해 표면의 리만 메트릭으로 무한히 인코딩됩니다.19세기와 20세기 초에는 R에 포함된³ 표면만 고려되었고 지표는 표면의 국소 매개변수화에서 지점마다 부드럽게 변화하는 2×2 양의 확정 행렬로 제공되었다.국지적 매개 변수화와 좌표 변경의 개념은 오늘날 지구가 지도에 의해 정확히 지도되는 것처럼 매끄러운 구조가 다지관의 국지적 차트에 의해 주어지는 위상 공간인 다지관의 현재 추상적 개념을 통해 나중에 공식화되었습니다.같은 영역의 다른 차트 간의 좌표 변화는 원활해야 한다.실제 지도의 등고선이 실제 거리를 계산하기 위해 지구 표면의 국지적 왜곡을 고려하면서 표고 변화를 인코딩하는 것처럼, 리만 메트릭은 각 국지 차트에서 "작은" 거리와 영역을 기술합니다.각 국소 차트에서 리만 메트릭은 각 점에 2×2 양의 확정 행렬을 매끄럽게 할당함으로써 주어진다. 다른 차트를 취하면, 행렬은 좌표 변화의 야코비 행렬에 따라 변환된다.그러면 다지관은 2차원 리만 다지관의 구조를 가집니다.

형상 연산자

가우스 맵 n의 미분 dn은 형상^[56] 연산자 또는 와인가텐 맵으로 알려진 외인성 곡률의 유형을 정의하는 데 사용할 수 있습니다.이 연산자는 처음에 빌헬름 블라쉬케의 연구에서 암묵적으로 나타났고 나중에 부랄리-포르티와 ^[57]부르가티의 논문에서 명시적으로 나타났다.표면의 각 점 x에서, 접선 공간은 내부 곱 공간이기 때문에, 형상_x 연산자 S는 공식에 의해 이 공간의 선형 연산자로 정의될 수 있다.

${\displaystyle (S_{x}v,w)=(dn(v),w)}$

탄젠트 벡터 v, w(dn(v)와 w는 둘 다 ^[a]E에³ 있기 때문에 내부곱은 의미가 있음)의 경우.오른쪽은 v와 w에서 대칭이므로 형상 연산자는 접선 공간에서 자가 접합됩니다.S의_x 고유값은 x의 주 곡선 k와₁₂ k입니다.특히 한 점에서 형상연산자의 결정식은 가우스 곡률이지만, 평균 곡률이 형상연산자의 트레이스의 절반이기 때문에 다른 정보도 포함한다.평균 곡률은 외적 불변량입니다.내적 기하학에서 실린더는 발전가능하며, 이는 가우스 곡률이 동일하게 사라지기 때문에 그것의 모든 조각이 본질적으로 평면의 조각과 구별할 수 없다는 것을 의미한다.그러나 평균 곡률은 0이 아니기 때문에 외부적으로는 평면과 다릅니다.

마찬가지로 형상 연산자는 접선 공간상의 선형 연산자 S_p: TM_p→TM로_p 정의할 수 있습니다.n이 M에 대한 단위 정규 필드이고 v가 탄젠트 벡터일 경우

${\displaystyle S(v)=\pm \displayla _{v}n}$

(정의에 + 또는 -를 사용할지 여부에 대한 표준적인 합의는 없습니다).

일반적으로 각 점에서 형상 연산자의 고유 벡터와 고유 값에 따라 각 점에서 표면이 휘어지는 방향이 결정됩니다.고유값은 표면의 주곡선에 해당하고 고유 벡터는 해당 주곡선에 해당합니다.주방향은 표면에 내장된 곡선이 최대 및 최소 곡률을 가지기 위해 이동해야 하는 방향을 지정합니다. 이 방향은 주곡선에 의해 지정됩니다.

지표면의 측지선 곡선

끝점 사이의 길이를 최소화하는 표면의 곡선을 측지학이라고 합니다. 두 점 사이에 늘어선 탄성 띠의 모양입니다.수학적으로 그것들은 상미분 방정식과 변분 미적분을 사용하여 기술된다.표면의 미분 기하학은 측지학 연구를 중심으로 회전한다.2차원 국부 차트 상의 모든 리만 측정이 3차원 유클리드 공간에 포함된 것에서 발생하는지는 여전히 미해결이다: 측지학의 이론은 측정의 성분이 분석적일 때 이것이 사실이라는 것을 보여주기 위해 사용되었다.

측지학

[a, b]의 t에 대한 차트에서 구간별 평활 경로 c(t) = (x(t), y(t)가 주어지면, 그 길이는 다음과 같이 정의된다.

${\displaystyle L(c)=\int _{a}^{b}(E{\dot {x}}^2}+2F{\dot {x}}{\dot {y}}+G{\dot {y}^2}^{\frac {1}{2}},dt}$

에너지를 소비하다

${\displaystyle E(c)=\int _{a}^{b}(E{\dot {x}}^2}+2F{\dot {x}}{\dot {y}}+G{\dot {y}^{2}}, dt.}$

길이는 경로의 매개 변수화와 독립적입니다.오일러-라그랑주 방정식에 의해, 만약 c(t)가 길이를 최소화하는 경로이고, 호 길이에 의해 매개변수가 지정된다면, 그것은 오일러 방정식을 만족시켜야 한다.

${{displaystyle {dot {x}}+\Gamma _{11}^{1}{\dot {x}^{2}+2\Gamma _{12}^{1}{\dot {y}^{1}{\gamma _{2}=0}$

${{displaystyle {dot {y}}+\Gamma _{11}^{2}{\dot {x}^2}{\dot {y}}+\Gamma _{22}^2}{\dot {y}{2}{\dot {y}=0}$

Christofel 기호 are는^k
_ij 다음과 같이 지정됩니다.

$\displaystyle \Gamma _{ij}^{k}=sum _{m}g^{km}(\sum _{m}g^{km}(\sum _{m}g_{im}+\sum _{m}g_{ij})}}$

여기서₁₁ g = E, g₁₂ = F, g₂₂ = G 및 g는^ij g에 대한_ij 역행렬이다.오일러 방정식을 만족시키는 경로를 측지선이라고 합니다.코시-슈바르츠 부등식에 의해 에너지를 최소화하는 경로는 호 길이로 분류된 측지선 매개변수에 불과하며, 측지선의 경우 매개변수 t는 호 ^[58]길이에 비례한다.

측지 곡률

방향 표면에서 호 길이로 매개 변수화된 곡선 c(t) 지점의 측지선 곡률_g k는 다음과^[59] 같이 정의된다.

${\displaystyle k_{g}=displayddot {c}(t)\cdot \mathbf {n}(t)}$

여기서 n(t)은 표면의 곡선에 수직인 "표준" 단위이며 단위 접선 벡터 θ(t)를 +90°의 각도로 회전시켜 구성합니다.

• 한 지점의 측지선 곡률은 해당 지점 근처의 메트릭에만 따라 고유 불변량이다.
• 지표면의 단위속도곡선은 곡선의 모든 지점에서 측지곡선이 사라지는 경우에만 측지곡선이다.
• 매립면에서의 단위속도곡선 c(t)는 그 가속도 벡터 cθ(t)가 표면에 대하여 법선일 경우에만 측지선이다.

측지선 곡률은 지표면의 곡선이 측지선으로부터 얼마나 떨어져 있는지를 정확하게 측정합니다.

직교 좌표

아래에서 설명하는 측지선 극좌표와 같이 좌표 차트 전체에서 F = 0이면 x 및 y 극좌표에 평행한 선의 영상은 직교하며 직교 좌표를 제공합니다.만약 H게 국가 주의적 관점에서 서술(EG).mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1⁄2.그 가우스 곡률 by[60] 주어진다.

$\displaystyle K=-{1 \over 2H}\left[\partial _{x}\frac {G_{x}}{H}}\right)+\partial _{y}\left({\frac {E_{y}}){H}}\right)\right]}$

E = 1이 추가되어 H = G일^1⁄2 경우, 측지선(x(t),y(t))와 선 y = 상수 사이의 교차점에서의 각도 θ는 다음 방정식으로 구할 수 있다.

$(\displaystyle\tan\varphi=H\cdot{frac{y}{\dot{x}})$

γ의 도함수는 ^[61]가우스의 고전적인 도함수 공식에 의해 주어진다.

$(\displaystyle\dot {varphi }}=-H_{x}\cdot {y}).}$

측지선 극좌표

지표면에 메트릭이 지정되고 기준점이 고정되면 기준점과 충분히 가까운 각 점을 연결하는 고유한 측지학이 있습니다.기준점의 측지선 방향과 거리에 따라 다른 끝점이 고유하게 결정됩니다.따라서 이 두 비트의 데이터(방향과 크기)에 따라 기준점에서의 접선 벡터가 결정됩니다.접선 벡터에서 끝점까지의 지도는 기준점 근방을 부드럽게 쓸어내고 "지수 지도"라고 불리는 것을 정의하여 해당 기준점에서 로컬 좌표 차트를 정의합니다.쓸려나간 이웃은 유클리드 공간의 공과 유사한 특성을 가지고 있다. 즉, 유클리드 공간의 어떤 두 점이라도 독특한 측지선에 의해 결합된다.이 특성을 "지오데식 볼록성"이라고 하며 좌표를 "정규 좌표"라고 합니다.정상 좌표를 명시적으로 계산하려면 측지학이 만족하는 미분 방정식을 고려해야 합니다.볼록성 특성은 가우스의 보조개념과 일반화의 결과이다.대략적으로 말하면, 기준점에서 시작하는 측지학은 기준점을 중심으로 하는 고정 반지름의 구를 직각으로 절단해야 한다는 것이다.지오데식 극좌표는 기점의 접선 벡터상의 극좌표와 지수맵을 조합하여 구한다.그리고 나서 표면의 가우스 곡률은 유클리드 메트릭에서 지점에서 메트릭의 2차 편차에 의해 주어진다.특히 가우스 곡률은 측정 기준의 불변량인 가우스의 유명한 이론마 에그리엄이다.곡률을 이해하는 편리한 방법은 가우스에 의해 먼저 고려되고 나중에 야코비에 의해 일반화되는 상미분 방정식에서 유래하며, 두 개의 다른 점에 대한 상좌표의 변화에서 발생한다.가우스-야코비 방정식은 가우스 곡률을 계산하는 또 다른 방법을 제공합니다.기하학적으로, 끝점이 작은 곡선 세그먼트를 따라 변화할 때 지오데식(^[62]geodic)을 따라 벡터 필드인 야코비 필드에 기록된 데이터를 통해 고정 기준점에서 지오데식에게 어떤 일이 일어나는지 설명합니다.가우스와 자코비 이후 1세기 25분 후, Marston Morse는 무한 차원 경로의 ^[63]힐베르트 다양체에 대한 에너지 함수의 2차 도함수 측면에서 자코비 장의 보다 개념적인 해석을 제공했습니다.

지수 지도

상미분방정식 이론은 f(t, v)가 매끄럽다면 초기 조건 v₀(0) = v인 미분방정식 dv/dt = f(t, v)는 t가 충분히 작을 수 있는 고유한 해를 가지며 해는 t와₀ v에 부드럽게 의존한다는 것을 보여준다.이는 주어진 지점 p = (x₀, y₀)에서 충분히 작은 탄젠트 벡터 v에 대해 c(0) = (x₀, y₀) 및 θ_v(0) = v로_v (-2, 2)에 정의된 측지선 c_v(t)가 있음을 의미한다. 더욱이 s 1 1이면 c = c_v(st)이다_sv.지수 맵은 다음과 같이 정의됩니다.

exp_p(v) = c_v (1)

디스크 'v' <와 p 근방의 차이동형성을 나타냅니다.일반적으로 exp(v)로의_p 맵 송신(p, v)은 (p, p) 근방의 로컬 차이동형을 나타냅니다.지수 지도는 ^[64]p 근처의 측지선 정규 좌표를 제공합니다.

정규 좌표 계산

정규 테일러 급수 확장으로서 정규 좌표 u, v에 대한 변수 변경을 계산하는 표준 기법(예: Berger(2004) 참조)이 있다.(0,0)에서 x, y 좌표가 국소적으로 직교하는 경우,

x(u,v) = αu + L(u,v) + δ(u,v) + …

y(u,v) = βv + M(u,v) + μ(u,v) + …

여기서 L, M은 2차 및 μ, μ 입방체의 균질 다항식(u 및 v)이다. u와 v가 고정되면 x(t) = x(tu,tv) = y(tu,tv)는 오일러 방정식의 공식 멱급수 해로 간주될 수 있다. 이 값은 α, β, L, L, M, δ, μ, μ, μ, μ

가우스 보조군

이들 좌표에서 행렬 g(x)는 g(0) = I를 만족하며 선 t δ tv는 0을 통과하는 측지선이다.오일러 방정식은 행렬 방정식을 의미한다

g(v)v = v,

보통 가우스 레마라고 불리는 중요한 결과기하학적으로 그것은 다음과 같이 기술되어 있다.

0까지의 측지선은 0을 중심으로 하는 원을 직교로 절단합니다.

극좌표(r,),)를 취하면 메트릭은 다음과 같은 형식을 갖습니다.

ds² = dr² + G(r,190) dµ².

측지 좌표에서는 0을 통한 측지선이 길이를 최소화하는 것을 쉽게 확인할 수 있습니다.리만 다양체의 위상은 거리 함수 d(p,q), 즉 p와 q 사이의 부분적 평활 경로 길이의 최소값에 의해 주어진다.이 거리는 측지학으로 국소적으로 실현되므로 정상 좌표에서 d(0,v) = "v"이다.반지름 θ가 충분히 작을 경우 가우스 레마를 약간 선명하게 하면 지수맵 아래의 디스크 θvθ < θ의 화상 U가 측지학적으로 볼록하다는 것을 알 수 있다.즉, U의 어느 2개 점에서도 ^[65][66]U의 전체가 U내에 놓여 있는 하나의 측지학이 결합되어 있다.

이론마 에그리움

가우스의 이론 이론 이론, "주목할 만한 정리"는 표면의 가우스 곡률은 메트릭의 관점에서만 계산될 수 있으며, 따라서 표면의 본질적인 불변량이며, E에³ 등각적 내장 및 좌표 변환에 따라 변하지 않는다는 것을 보여준다.특히 표면의 등각은 가우스 ^[67]곡률을 유지합니다.

이 정리는 다음과 같이 정규 좌표(u, v)로 주어진 메트릭의 멱급수 확장의 관점에서 표현될 수 있다.

ds² = du² + dv² - K(u dv – v du)/²12 + …

가우스-야코비 방정식

p의 정규 좌표에서 인근 지점 q의 정규 좌표까지 좌표 변화를 취하면 H(r,190) = G(r,190)^1⁄2로 만족하는 Sturm-Liouville 방정식이 생성되며, 가우스에 의해 발견되고 나중에 야코비에 의해 일반화된다.

Hrr = –KH

q에서 이 좌표 변화의 야코비안은 H와 같다_r.이것은 가우스 곡률의 본질적인 특성을 확립하는 또 다른 방법을 제공한다.H(r,θ)는 θ 방향의 선 요소의 길이로 해석될 수 있기 때문에 가우스-야코비 방정식은 ^[68]가우스 곡률에 의해 점으로부터 멀어질 때 기하학적 표면에서의 측지학 확산이 측정된다는 것을 보여준다.

라플라스-벨트라미 연산자

로컬 메트릭이 있는 지표면

${\displaystyle ds^{2}=E,dx^{2}+2F,dx,dy+G,dy^{2}}$

및 Laplace-Beltrami 연산자

$\displaystyle \Delta f={1 \over H}\left(\partial _{x}{G \over H}\partial _{x}f-\partial _{y}f-\partial _{y}{F \over H}\partial _{x}\oper H}_E}_{\partial _{x}$

여기서² H = EG - F², 점에서의 가우스 곡률은 다음 공식에^[69] 의해 주어진다.

$(\displaystyle K=-3\lim _{r\right 화살표 0}\Delta (\log r),}$

여기서 r은 점으로부터의 측지 거리를 나타냅니다.

가우스가 먼저 고려하는 등온 좌표에서 메트릭은 특수 형식이어야 합니다.

$(\displaystyle ds^{2}=e^{\varphi})(표준^{2}+dy^{2}).\,}$

이 경우 라플라스-벨트라미 연산자는 다음과 같이 주어진다.

${\displaystyle \Delta = e^{-\varphi}\leftfrac {\frac ^{2}+{\frac ^{2}}{\frac y^{2}}\right}}$

θ는 Liouville의 방정식을^[70] 만족한다.

$\displaystyle \Delta \varphi =-2K,}$

등온 좌표는 지금까지의 모든 증명은 편미분 ^[71]방정식에 대한 중요하지 않은 결과에 의존하지만 지표상의 모든 점 근처에 존재하는 것으로 알려져 있다.최소 ^[72]표면에 대한 기본적인 증거가 있습니다.

가우스-보네 정리

구면 또는 쌍곡면상에서 측지삼각형, 즉 모든 변이 측지학인 삼각형의 면적은 내부각과 θ의 합계의 차이에 비례한다.비례성의 상수는 이러한 표면에 대한 상수인 가우스 곡률일 뿐입니다.토러스의 경우 차이가 0이므로 가우스 곡률이 0임을 알 수 있습니다.구면, 쌍곡선 및 고등학교 삼각법의 표준 결과입니다(아래 참조).가우스는 측지 삼각형의 내부에 걸친 가우스 곡률의 적분이 이 각도 차이 또는 초과와 동일하다는 것을 보여줌으로써 이러한 결과를 임의 표면에 일반화했다.그의 공식은 측지삼각형의 면적 초과 각도의 한계로 점 근처에서 가우스 곡률을 계산할 수 있음을 보여주었다.닫힌 표면은 측지삼각형으로 분해될 수 있기 때문에 공식을 사용하여 표면 전체에 걸친 곡률의 적분을 계산할 수도 있습니다.현재 가우스-보넷 정리라고 불리는 것의 특별한 경우로서, 가우스는 이 적분이 항상 오일러 특성이라고 불리는 표면의 위상 불변량인 정수의 2µ배라는 것을 증명했다.이 불변량은 삼각 측량이라고도 하는 분해에서 삼각형의 꼭지점, 모서리 및 면의 수로 조합하여 계산하기 쉽습니다.분석과 위상 사이의 이러한 상호작용은 아티야-싱어 지수 정리로 정점에 이른 기하학의 많은 후발 결과들의 선구자였다.특히 곡률의 특성은 표면의 위상에 제약을 가한다.

측지 삼각형

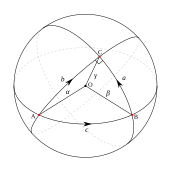
가우스는 δ가 정점 A, B, C에서 각도 α, β 및 θ를 갖는 표면의 측지삼각형일 경우,

$\displaystyle \int _{\Delta }K,dA=\alpha +\display +\display -\pi .}$

실제로 원점 A와 AB, AC 극각 0과 α의 반지름을 갖는 측지선 극좌표를 취한다.

${\displaystyle {\delta }K,dA&=\int _{\Delta }KH,dr,d\theta =-\int _{0}^{\alpha }\int _{0}^{\theta }}\!H_{r},dr,d\theta \\&=\int _{0}^{\alpha }1-H_{r}(r_{\theta},\theta ),d\int _{0}^{\alpha }d\theta +\int _{\pi -\theta }^{\h}\hta }!\!d\varphi \\&=\alpha +\contrace -\pi ,\end {aligned}}$

여기서 두 번째 등식은 가우스-야코비 방정식에서, 네 번째 등식은 가우스의 직교 좌표(r,θ)에서 도출된다.

가우스의 공식은 점 근처의 연속적으로 작은 측지삼각형에 대한 면적에 대한 각도 초과 α + β + δ - δ의 한계로 점에서의 곡률을 계산할 수 있음을 보여준다.임의의 작은 ^[49]측지삼각형의 각도초과의 부호에 따라 표면이 정성적으로 정 또는 부곡된다.

가우스-보네 정리

모든 콤팩트 지향 2-매니폴드 M은 작은 측지삼각형으로 삼각측량될 수 있기 때문에 다음과 같이 된다.

$\displaystyle \int _{M}KdA=2\pi\chi(M)}$

여기서 θ(M)는 표면의 오일러 특성을 나타낸다.

실제로 F면, E면 및 V 정점이 있으면 3F = 2E이고 왼쪽은 2µV – δF = 2µF(V – E + F) = 2µF(M)와 같습니다.

이것은 유명한 가우스-보넷 정리이다: 이것은 가우스 곡률의 적분이 다양체의 위상 불변량, 즉 오일러 특성임을 보여준다.이 정리는 많은 방법으로 해석될 수 있다; 아마도 가장 멀리 있는 것 중 하나는 아티야-싱어 지수 정리의 가장 단순한 경우 중 하나인 M 위의 타원 미분 연산자에 대한 지수 정리이다.가우스-보네 정리를 사용하여 증명될 수 있는 또 다른 관련 결과는 M 위의 벡터장에 대한 푸앵카레-홉프 지수 정리이다: 이 점들의 지수들의 합은 오일러 특성과 같으며, 여기서 각 0, t로 분리된 작은 원에 다음과 같이 정의된다:벡터 필드는 단위 원에 맵을 정의합니다. 색인은 이 맵의 와인딩 번호입니다.)^[49][73][74]

곡률 및 매립

표면 M의 가우스 곡률이 모든 면에서 양의 경우, 오일러 특성은 양수이므로 M은 S와² 동형(따라서 미분형)이 됩니다.또한 표면이 E에³ 등각적으로 포함되어 있는 경우, 가우스 맵은 명시적 미분 동형을 제공한다.Hadamard가 관찰한 바와 같이, 이 경우 표면은 볼록하다. 이 볼록성 기준은 평면 곡선의 볼록성에 대한 잘 알려진 두 번째 미분 기준의 2차원 일반화로 볼 수 있다.힐버트는 모든 등각적으로 내장된 닫힌 표면에는 양의 곡률점이 있어야 한다는 것을 증명했다.따라서 비양성 곡률의 닫힌 리만 2-매니폴드는 절대 E에³ 등각적으로 삽입될 수 없다. 그러나 아드리아노 가르시아가 준정형 매핑을 위해 벨트라미 방정식을 사용하는 것을 보여주었듯이, 이것은 일부 적합 등가 ^[75]메트릭에 대해 항상 가능하다.

일정한 곡률의 표면

일정한 곡률 0, +1 및 –1의 단순하게 연결된 표면은 유클리드 평면, E의³ 단위구 및 쌍곡면입니다.이들 각각은 기하학 연구에 사용할 수 있는 등각선 G를 보존하는 방향의 전이적 3차원 Lie 그룹을 가지고 있다.2개의 비콤팩트 표면 각각은 G/K의 몫으로 동정할 수 있다.여기서 K는 G의 최대 콤팩트 부분군이다.여기서 K는 SO(2)와 동형이다.필요한 경우 일정한 계수로 메트릭을 스케일링한 후 일정한 가우스 곡률의 다른 닫힌 리만 2-매니폴드 M은 이 세 가지 표면 중 하나를 범용 피복 공간으로 갖는다.배향 가능한 경우, M의 기본군 δ는 G의 비틀림 없는 균일한 부분군으로 동정할 수 있고, 그 후 이중 코세트 공간 δ\G/K로 동정할 수 있다.구면 및 유클리드 평면의 경우, 구면 자체와 R의² 몫으로서 이산적인 부분군 2에 의해 얻을 수 있는 토리뿐이다.g δ2속 닫힌 표면의 경우, δ로 얻을 수 있는 리만 표면의 모듈리 공간은 이러한 모든 부분군에 걸쳐 변화하며, 실차원 6g~^[76]6을 가진다. 푸앵카레의 균등화 정리에 따르면, 모든 방향성 닫힌 2-매니폴드는 일정한 곡률 0, +1 또는 –1의 표면과 등가된다.즉, 메트릭에 양의 스케일링 계수를 곱함으로써 가우스 곡률은 이들 값 중 정확히 하나를 취할 수 있습니다(M의 ^[77]오일러 특성 부호).

유클리드 기하학

유클리드 평면의 경우, 대칭군은 회전 그룹에 의한 2차원 변환 ^[78]그룹의 반직접 산물인 유클리드 운동군이다.측지선은 직선이며 기하학은 삼각형의 코사인 규칙과 같은 삼각형의 기본 공식으로 부호화된다. 예를 들어 변 a, b, c 및 각도α, β, β:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab,\cos \cos \cisco.}$

평탄한 토리는 격자로 R의² 몫, 즉 랭크 2의 자유 아벨 부분군을 취함으로써 얻을 수 있다.이러한 닫힌 표면에는 E에³ 등각계 매립물이 없습니다.그럼에도 불구하고, 그들은 E에⁴ 등각 함몰을 인정한다; 가장 쉬운 경우, 이것은 토러스가 두 개의 원의 산물이고 ^[79]각 원이² E에 등각 함몰될 수 있다는 사실에서 비롯된다.

구면 기하학

E에서³ 단위구² S의 등각군은 직교군 O(3)이며, 회전군 SO(3)는 방향을 보존하는 등각체의 하위그룹이다.SO(3)의 대척점 맵과 함께 x를 ^[80]–x로 보내는 직접 곱입니다.그룹 SO(3)는 S에 대해² 전이적으로 작용한다.단위 벡터(0,0,1)의 스태빌라이저 서브그룹은 SO(2)로 식별될 수 있으므로 S = SO(3)/SO(2)이다².

구의 두 점 사이의 측지학이 이러한 끝점을 가진 대원호입니다.점이 대척점이 아닌 경우 점 사이에 고유한 최단 측지선이 있습니다.측지학은 이론적으로도 설명할 수 있다: 북극(0,0,1)을 통과하는 각 측지학은 적도의 대척점을 통과하는 축을 중심으로 회전하는 부분군의 궤도이다.

구면 삼각형은 구면상의 측지 삼각형이다.길이 θ 미만의 대원호에서 형성된 변 BC, CA, AB의 구면상의 점 A, B, C로 정의된다.변의 길이가 a, b, c이고 변 α, β, θ 사이의 각도가면 구면 코사인 법칙은 다음과 같이 기술한다.

$(\displaystyle\cos c=\cos a,\cos b+\sin a,\sin b,\cos \cos \cos)}$

삼각형의 넓이는 다음과 같습니다.

면적 = α + β + β - β.

북극으로부터의 입체 투영을 이용하여, 구는 확장된 복소 평면 C { {}.}로 식별할 수 있다.명시적 맵은 다음과 같습니다.

${\displaystyle \pi (x,y,z)={x+iy \over 1-z}\equiv u+iv}$

이 대응 하에서는 S의 모든² 회전이 SU(2)의 뫼비우스 변환에 해당하며,^[81] 부호까지 고유하다.복소 평면의 좌표(u, v)에 관하여, 구면 메트릭은^[82]

$\displaystyle ds^{2}={4(du^{2}+dv^{2}) \over(1+u^{2}+v^{2})^{2}.}$

단위 구는 일정한 곡률 +1을 갖는 고유한 닫힌 방향성 표면입니다.비율 SO(3)/O(2)는 실제 투영 평면으로 식별할 수 있습니다.방향성이 없으며 대척점 맵(-1 곱하기)에 의해 S의² 몫으로 설명될 수 있다.구는 단순하게 연결되어 있지만 실제 투영 평면은 기본 그룹₂ Z를 가집니다.O(2)의 유한 부분군과 플라톤 고체의 대칭군에 해당하는 SO(3)의 유한 부분군은 S에 자유롭게² 작용하지 않으므로, 대응하는 몫은 2-매니폴드가 아니라 단지 오비폴드이다.

쌍곡선 기하학

비유클리드^[83] 기하학은 가우스의 편지에서 처음 논의되었는데, 가우스는 19세기 초에 광범위한 계산을 했고, 가우스를 개인적으로 회람시키기는 했지만, 그는 그것을 출판하지 않기로 결정했다.1830년 로바체프스키와 1832년 가우스의 특파원 중 한 명의 아들인 볼야이는 독립적으로 이 새로운 기하학의 합성판을 출판했는데, 이 때문에 그들은 혹독한 비판을 받았다.그러나 1868년이 되어서야 벨트라미는 1871년 클라인과 1882년 푸앵카레가 클라인의 쌍곡기하학에 대한 구체적인 해석 모델을 제시하였다.등장한 2차원 쌍곡선 기하학의 네 가지 모델은 다음과 같습니다.

• Beltrami-Klein 모델
• Poincaré 디스크
• 푸앵카레 상부 하프 플레인
• 3차원 민코프스키 공간에서 빌헬름 킬링의 쌍곡선 모형.

디스크를 기반으로 한 첫 번째 모델은 측지학이 실제로 선분(즉, 열린 단위 디스크와 유클리드 선의 교차점)이라는 장점이 있습니다.마지막 모델은 3차원 유클리드 공간에서 단위구와 완전히 평행한 구조를 제공한다는 장점이 있다.그러나 복잡한 해석과 기하학에 적용되기 때문에 Poincaré 모델이 가장 널리 사용됩니다. 디스크와 상부 하프 플레인 간의 뫼비우스 변환 덕분에 서로 교환할 수 있습니다.

허락하다

${\displaystyle D=\{z,\colon z <1\}}$

Poincaré 메트릭을 사용하여 복잡한 평면에서 Poincaré 원반이 됩니다.

${\displaystyle ds^{2}={4(syslog^{2}+dy^{2}) \over(1-x^{2}-y^{2})^{2}}.}$

극좌표(r, θ)에서 메트릭은 다음과 같이 주어진다.

$\displaystyle ds^{2}={4(dr^{2}+r^{2},d\theta ^{2}) \over(1-r^{2}^2})^{2}}.}$

곡선의 길이 θ:[a,b] → D는 다음 공식에 의해 주어진다.

$\displaystyle \ell (\displaystyle )=\int _{a}^{b}{2 \display ^{\prime }(t), dt \over 1-\display (t)^{2}}.}$

그룹 G = SU(1,1)는 다음과 같다.

${\displaystyle G=\left\{\begin{pmatrix}\alpha &\in\mathbf {C}, \alpha 、 \alpha } 、 \ end {pmatrix } : \ alpha 、 \ light }$

D에서 뫼비우스 변환에 의해 과도적으로 작용하며 0의 안정기 부분군은 회전군이다.

$({displaystyle K=\left}{\begin{pmatrix}\zeta &0&{\오버라인{zeta }}\end{pmatrix}):\zeta \in \mathbf {C}, \zeta = 1\right\}).}$

몫군 SU(1,1)/±I는 D의 배향 보존 등각체의 군이다.D의 임의의 2점 z, w는 z, w를 통과하고 경계원에 직교하는 원 또는 직선의 부분에 의해 주어지는 고유 측지학에 의해 결합된다.z와 w 사이의 거리는 다음과 같습니다.

${\displaystyle d(z,w)=2\tanh ^{-1}{\frac {z-w}{ 1-{\overline {w}}z}}}.}$

특히 d(0,r) = 2 tanh⁻¹ r 및 c(t) = 1/2 tanh t는 실제 축을 따라 0을 통과하는 측지선이며, 호 길이로 매개변수를 구한다.

이 메트릭에 의해 정의된 토폴로지는 메트릭 공간(D,d)이 완전하지만 일반적인 유클리드 토폴로지와 동일합니다.

쌍곡선 삼각형은 이 메트릭에 대한 측지선 삼각형입니다. D의 세 점은 쌍곡선 삼각형의 꼭지점입니다.만약 변이 대응하는 각도α, β, θ를 가진 길이 a, b, c를 갖는다면, 쌍곡 코사인 규칙은 다음과 같이 기술한다.

$(\displaystyle\cosh c=\cosh a, cosh b-\sinh a,\sinh b,\cos \cos \cos)}$

쌍곡선 삼각형의 면적은 다음과 같이 주어진다^[84].

면적 = α – β – β.

유닛 디스크와 상부 하프 플레인

$\displaystyle H=\{w=x+iy,\colon\,y>0\}$

뫼비우스 변환에 의해 등가적이다.

$({displaystyle w=i{1+z\over 1-z},,z={w-i\over w+i})$

이 대응관계에서 H에 대한 뫼비우스 변환에 의한 SL(2,R)의 작용은 D에 대한 SU(1,1)의 작용에 해당한다.H의 메트릭은

$\displaystyle ds^{2}={display^{2}+dy^{2} \over y^{2}}.}$

뫼비우스 변환에서는 선 또는 원이 보존되기 때문에 측지학은 다시 실제 축에 직교하는 선 또는 원으로 설명됩니다.

Poincaré 메트릭을 사용하는 단위 디스크는 일정한 곡률 -1을 가진 단순 연결 방향 2차원 리만 다양체입니다.이 성질을 가진 지향성 폐표면 M은 그 보편 피복공간으로서 D를 가진다.기본 그룹은 다음과 같은 방식으로 SU(1,1)의 비틀림 없는 콤팩트 서브그룹 δ과 식별할 수 있다.

$({displaystyle M=\Gamma\백슬래시 G/K})$

이 경우 δ는 최종적으로 제시된 그룹입니다.발생기와 관계는 M의 닫힌 측지선에 기하학적으로 대응하는 D(또는 H)의 측지학적 볼록 기본 측지학적 다각형으로 부호화된다.

예를 들면.

• 2속 볼자 표면
• 3속 클라인 4진수
• 7속 맥비스의 표면
• 14속 최초의 후르비츠 세쌍둥이

균일화

가우스 곡률 K의 지향성 폐표면 M이 주어졌을 때, M의 메트릭은 계수^2u e만큼 스케일링함으로써 적합하게 변경할 수 있다.그러면 새로운 가우스 곡률 Kµ는 다음과 같이 표시됩니다.

$(\displaystyle K^{\prime }(x)=e^{-2u}(K(x)-\Delta u),}$

여기서 δ는 원래 메트릭의 Laplacian입니다.따라서 주어진 표면이 일정한 곡률 KΩ의 메트릭과 일치함을 보여주기 위해 다음과 같은 리우빌 방정식을 푸는 것으로 충분하다.

$\displaystyle \Delta u=K^{\prime}e^{2u}+K(x)}$

M이 오일러 특성 0을 가질 때, 토러스와 미분형상인 Kθ = 0이므로, 이는 해답에 해당한다.

$\displaystyle \Delta u=K(x).}$

표준 타원 이론에 따르면, 이것은 가우스-보넷 ^[85]정리에 의해 K/M의 적분이 0이기 때문에 가능하다.

M이 음의 오일러 특성을 가질 때, KΩ = -1이므로 풀어야 할 방정식은 다음과 같습니다.

$\displaystyle \Delta u=-e^{2u}+K(x)}$

Neil Trudinger에 의한 Sobolev 공간에서의 지수 맵의 연속성을 사용하여, 이 비선형 방정식은 항상 풀 ^[86]수 있습니다.

마지막으로 2-구체의 경우 Kµ = 1이며 방정식은 다음과 같습니다.

$\displaystyle \Delta u=e^{2u}+K(x)}$

리만-로흐 정리와 같은 고전적인 결과는 항상 ^[87]해를 가지고 있다는 것을 의미하지만, 지금까지 이 비선형 방정식은 직접적으로 분석되지 않았다.리처드 S에 의해 개발된 리치 플로우 방식. 해밀턴은 ^[88]존재를 증명하기 위해 비선형 편미분 방정식에 기초한 또 다른 존재 증거를 제공한다.실제로 S의² 컨포멀 메트릭에 대한 Ricci 흐름은 함수 u(x, t)에서 다음과 같이 정의됩니다.

$({displaystyle u_{t}=4\pi -K'(x,t)=4\pi -e^{-2u}(K(x)-\Delta u).}$

유한 시간 후, Chow는 KΩ이 양수가 된다는 것을 보여주었다. 그 후 해밀턴의 이전 결과는 KΩ이 +1로 ^[89]수렴한다는 것을 보여주는 데 사용될 수 있었다.Ricci 흐름에 대한 이러한 결과가 나오기 전에, Osgood, Phillips & Sarnak(1988)는 로그 검출기_g δ에 의해 정의된 리만 메트릭 g의 흐름에 기초하여 균일화를 위한 대체적이고 기술적으로 단순한 접근방식을 제공했다.

1988년에 발견된 타원 연산자를 사용한 증거는 딩(2001)에서 찾을 수 있다.G를 δG = 1 + 4θ를_P 만족하는 S 위의 Green의² 함수라고 하자. 여기서 θ는_P S의² 고정점 P에서의 점 측정값이다.δv = 2K – 2의 방정식은 평활해 v를 가진다. 왜냐하면 오른쪽에는 가우스-보넷 정리에 의한 적분 0이 있기 때문이다.따라서 P로부터 θ = 2G + v는 θ = 2K를 만족한다.따라서₁ g = eg는^φ P의 보완체에서 일정한 곡률 0의 완전한 메트릭이며, 따라서 평면에 대해 등각이다.입체 투영으로 구성하면, 예를 들어 P의 보체에 가우스 곡률 +1을 가질 수 있는^2u 매끄러운 함수 u가 있다.함수 u는 ^[b]S 전체에² 대해 자동으로 부드러운 함수까지 확장됩니다.

리만 접속 및 병렬 전송

는 리만 다양체의 개념 베른하르트 리만에 의해 19세기 중반에 시작되고 연결 툴리오 레비치비타,Élie 카르탕과 헤르만 바일에 의해 이른 20일 centu에 개발된 것의 출현 predated 가우스의 표면의 미분 기하학에 대한 고전적인 방법이 표준 초 approach[90].ry.연결, 공변 미분 및 병렬 전달의 개념은 곡률을 이해하는 보다 개념적이고 균일한 방법을 제공했으며, 이는 고차원 다양체에 대한 일반화를 가능하게 했을 뿐만 아니라 특성 클래스라고 ^[91]불리는 새로운 기하학적 불변성을 정의하기 위한 중요한 도구를 제공했다.공변 미분 및 연결을 사용하는 접근법은 오늘날 보다 고급 ^[92]교과서에서 채택된 접근법이다.

공변 미분

서페이스상의 접속은, 동등하지만, 동등하게 중요한 다양한 시점에서 정의할 수 있습니다.리만 접속 또는 Levi-Civita 접속.^[93]는 아마도 다지관 함수에 작용하는 1차 미분 연산자로 간주되는 벡터 필드를 접선 번들 또는 프레임 번들의 미분 연산자에 대해 가장 쉽게 이해할 수 있다.내장된 표면의 경우, 공변 도함수라고 불리는 벡터장 위의 연산자에 대한 리프트는 직교 투영으로 매우 간단하게 설명된다.실제로 R에³ 매설된 표면상의 벡터장은 표면에서 R에 대한³ 함수라고 볼 수 있다.다른 벡터 필드는 성분별로 미분 연산자로 작동합니다.결과 벡터 필드는 지표면에 접하지 않지만 지표면의 각 지점에서 접선 공간에 직교 투영하여 수정할 수 있습니다.20세기 초에 Ricci와 Levi-Civita가 깨달은 것처럼, 이 과정은 미터법에만 의존하며 Christofel 기호로 국지적으로 표현될 수 있다.

Parallel transport

Parallel transport of tangent vectors along a curve in the surface was the next major advance in the subject, due to Levi-Civita.^[49] It is related to the earlier notion of covariant derivative, because it is the monodromy of the ordinary differential equation on the curve defined by the covariant derivative with respect to the velocity vector of the curve. Parallel transport along geodesics, the "straight lines" of the surface, can also easily be described directly. A vector in the tangent plane is transported along a geodesic as the unique vector field with constant length and making a constant angle with the velocity vector of the geodesic. For a general curve, this process has to be modified using the geodesic curvature, which measures how far the curve departs from being a geodesic.^[65]

A vector field v(t) along a unit speed curve c(t), with geodesic curvature k_g(t), is said to be parallel along the curve if

• it has constant length
• the angle θ(t) that it makes with the velocity vector ċ(t) satisfies

${\displaystyle {\dot {\theta }}(t)=-k_{g}(t)}$

This recaptures the rule for parallel transport along a geodesic or piecewise geodesic curve, because in that case k_g = 0, so that the angle θ(t) should remain constant on any geodesic segment. The existence of parallel transport follows because θ(t) can be computed as the integral of the geodesic curvature. Since it therefore depends continuously on the L² norm of k_g, it follows that parallel transport for an arbitrary curve can be obtained as the limit of the parallel transport on approximating piecewise geodesic curves.^[94]

The connection can thus be described in terms of lifting paths in the manifold to paths in the tangent or orthonormal frame bundle, thus formalising the classical theory of the "moving frame", favoured by French authors.^[95] Lifts of loops about a point give rise to the holonomy group at that point. The Gaussian curvature at a point can be recovered from parallel transport around increasingly small loops at the point. Equivalently curvature can be calculated directly at an infinitesimal level in terms of Lie brackets of lifted vector fields.

Connection 1-form

The approach of Cartan and Weyl, using connection 1-forms on the frame bundle of M, gives a third way to understand the Riemannian connection. They noticed that parallel transport dictates that a path in the surface be lifted to a path in the frame bundle so that its tangent vectors lie in a special subspace of codimension one in the three-dimensional tangent space of the frame bundle. The projection onto this subspace is defined by a differential 1-form on the orthonormal frame bundle, the connection form. This enabled the curvature properties of the surface to be encoded in differential forms on the frame bundle and formulas involving their exterior derivatives.

This approach is particularly simple for an embedded surface. Thanks to a result of Kobayashi (1956), the connection 1-form on a surface embedded in Euclidean space E³ is just the pullback under the Gauss map of the connection 1-form on S².^[96] Using the identification of S² with the homogeneous space SO(3)/SO(2), the connection 1-form is just a component of the Maurer–Cartan 1-form on SO(3).^[97]

Global differential geometry of surfaces

Although the characterisation of curvature involves only the local geometry of a surface, there are important global aspects such as the Gauss–Bonnet theorem, the uniformization theorem, the von Mangoldt-Hadamard theorem, and the embeddability theorem. There are other important aspects of the global geometry of surfaces.^[98] These include:

• Injectivity radius, defined as the largest r such that two points at a distance less than r are joined by a unique geodesic. Wilhelm Klingenberg proved in 1959 that the injectivity radius of a closed surface is bounded below by the minimum of δ = π/√sup K and the length of its smallest closed geodesic. This improved a theorem of Bonnet who showed in 1855 that the diameter of a closed surface of positive Gaussian curvature is always bounded above by δ; in other words a geodesic realising the metric distance between two points cannot have length greater than δ.
• Rigidity. In 1927 Cohn-Vossen proved that two ovaloids – closed surfaces with positive Gaussian curvature – that are isometric are necessarily congruent by an isometry of E³. Moreover, a closed embedded surface with positive Gaussian curvature and constant mean curvature is necessarily a sphere; likewise a closed embedded surface of constant Gaussian curvature must be a sphere (Liebmann 1899). Heinz Hopf showed in 1950 that a closed embedded surface with constant mean curvature and genus 0, i.e. homeomorphic to a sphere, is necessarily a sphere; five years later Alexandrov removed the topological assumption. In the 1980s, Wente constructed immersed tori of constant mean curvature in Euclidean 3-space.
• Carathéodory conjecture: This conjecture states that a closed convex three times differentiable surface admits at least two umbilic points. The first work on this conjecture was in 1924 by Hans Hamburger, who noted that it follows from the following stronger claim: the half-integer valued index of the principal curvature foliation of an isolated umbilic is at most one.
• Zero Gaussian curvature: a complete surface in E³ with zero Gaussian curvature must be a cylinder or a plane.
• Hilbert's theorem (1901): no complete surface with constant negative curvature can be immersed isometrically in E³.

• The Willmore conjecture. This conjecture states that the integral of the square of the mean curvature of a torus immersed in E³ should be bounded below by 2π². It is known that the integral is Moebius invariant. It was solved in 2012 by Fernando Codá Marques and André Neves.^[99]
• Isoperimetric inequalities. In 1939 Schmidt proved that the classical isoperimetric inequality for curves in the Euclidean plane is also valid on the sphere or in the hyperbolic plane: namely he showed that among all closed curves bounding a domain of fixed area, the perimeter is minimized by when the curve is a circle for the metric. In one dimension higher, it is known that among all closed surfaces in E³ arising as the boundary of a bounded domain of unit volume, the surface area is minimized for a Euclidean ball.
• Systolic inequalities for curves on surfaces. Given a closed surface, its systole is defined to be the smallest length of any non-contractible closed curve on the surface. In 1949 Loewner proved a torus inequality for metrics on the torus, namely that the area of the torus over the square of its systole is bounded below by √3/2, with equality in the flat (constant curvature) case. A similar result is given by Pu's inequality for the real projective plane from 1952, with a lower bound of 2/π also attained in the constant curvature case. For the Klein bottle, Blatter and Bavard later obtained a lower bound of √8/π. For a closed surface of genus g, Hebda and Burago showed that the ratio is bounded below by 1/2. Three years later Mikhail Gromov found a lower bound given by a constant times g^1⁄2, although this is not optimal. Asymptotically sharp upper and lower bounds given by constant times g/(log g)² are due to Gromov and Buser-Sarnak, and can be found in Katz (2007). There is also a version for metrics on the sphere, taking for the systole the length of the smallest closed geodesic. Gromov conjectured a lower bound of 1/2√3 in 1980: the best result so far is the lower bound of 1/8 obtained by Regina Rotman in 2006.^[100]

Reading guide

One of the most comprehensive introductory surveys of the subject, charting the historical development from before Gauss to modern times, is by Berger (2004). Accounts of the classical theory are given in Eisenhart (2004), Kreyszig (1991) and Struik (1988); the more modern copiously illustrated undergraduate textbooks by Gray, Abbena & Salamon (2006), Pressley (2001) and Wilson (2008) might be found more accessible. An accessible account of the classical theory can be found in Hilbert & Cohn-Vossen (1952). More sophisticated graduate-level treatments using the Riemannian connection on a surface can be found in Singer & Thorpe (1967), do Carmo (2016) and O'Neill (2006).

See also

• Flatness (mathematics)
• Tangent vector
• Zoll surface

Notes

References

• Andrews, Ben; Bryan, Paul (2010), "Curvature bounds by isoperimetric comparison for normalized Ricci flow on the two-sphere", Calc. Var. Partial Differential Equations, 39 (3–4): 419–428, arXiv:0908.3606, doi:10.1007/s00526-010-0315-5, S2CID 1095459
• Arnold, V.I. (1989), Mathematical methods of classical mechanics, Graduate Texts in Mathematics, vol. 60 (2nd ed.), New York: Springer-Verlag, ISBN 978-0-387-90314-9; translated from the Russian by K. Vogtmann and A. Weinstein.
• Berger, Marcel (2004), A Panoramic View of Riemannian Geometry, Springer-Verlag, ISBN 978-3-540-65317-2
• Berger, Melvyn S. (1977), Nonlinearity and Functional Analysis, Academic Press, ISBN 978-0-12-090350-4
• Bonola, Roberto; Carslaw, H. S.; Enriques, F. (1955), Non-Euclidean Geometry: A Critical and Historical Study of Its Development, Dover, ISBN 978-0-486-60027-7
• Boothby, William M. (1986), An introduction to differentiable manifolds and Riemannian geometry, Pure and Applied Mathematics, vol. 120 (2nd ed.), Academic Press, ISBN 0121160521
• Cartan, Élie (1983), Geometry of Riemannian Spaces, Math Sci Press, ISBN 978-0-915692-34-7; translated from 2nd edition of Leçons sur la géométrie des espaces de Riemann (1951) by James Glazebrook.
• Cartan, Élie (2001), Riemannian Geometry in an Orthogonal Frame (from lectures delivered by É Cartan at the Sorbonne in 1926-27) (PDF), World Scientific, ISBN 978-981-02-4746-1^{[dead link]}; translated from Russian by V. V. Goldberg with a foreword by S. S. Chern.
• Cartan, Henri (1971), Calcul Differentiel (in French), Hermann, ISBN 9780395120330
• Chen, Xiuxiong; Lu, Peng; Tian, Gang (2006), "A note on uniformization of Riemann surfaces by Ricci flow", Proc. AMS, 134 (11): 3391–3393, doi:10.1090/S0002-9939-06-08360-2
• Chern, S. S. (1967), Curves and Surfaces in Euclidean Spaces, MAA Studies in Mathematics, Mathematical Association of America
• Chow, B. (1991), "The Ricci flow on a 2-sphere", J. Diff. Geom., 33 (2): 325–334, doi:10.4310/jdg/1214446319
• Courant, Richard (1950), Dirichlet's Principle, Conformal Mapping and Minimal Surfaces, John Wiley & Sons, ISBN 978-0-486-44552-6
• Darboux, Gaston, Leçons sur la théorie générale des surfaces, Gauthier-Villars Volume I (1887), Volume II (1915) [1889], Volume III (1894), Volume IV (1896).
• Ding, W. (2001), "A proof of the uniformization theorem on S²", J. Partial Differential Equations, 14: 247–250
• do Carmo, Manfredo P. (2016), Differential Geometry of Curves and Surfaces (revised & updated 2nd ed.), Mineola, NY: Dover Publications, Inc., ISBN 978-0-486-80699-0
• do Carmo, Manfredo (1992), Riemannian geometry, Mathematics: Theory & Applications, Birkhäuser, ISBN 0-8176-3490-8
• Eisenhart, Luther Pfahler (2004), A Treatise on the Differential Geometry of Curves and Surfaces (reprint of the 1909 ed.), Dover Publications, Inc., ISBN 0-486-43820-1
• Euler, Leonhard (1760), "Recherches sur la courbure des surfaces", Mémoires de l'Académie des Sciences de Berlin (published 1767), 16: 119–143.
• Euler, Leonhard (1771), "De solidis quorum superficiem in planum explicare licet", Novi Commentarii Academiae Scientiarum Petropolitanae (published 1772), 16: 3–34.
• Gauss, Carl Friedrich (1902), General Investigations of Curved Surfaces of 1825 and 1827, Princeton University Library translated by A.M. Hiltebeitel and J.C. Morehead; "Disquisitiones generales circa superficies curvas", Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores Vol. VI (1827), pp. 99–146.
  • Gauss, Carl Friedrich (1965), General Investigations of Curved Surfaces, translated by A.M. Hiltebeitel; J.C. Morehead, Hewlett, NY: Raven Press, OCLC 228665499.
  • Gauss, Carl Friedrich (2005), General Investigations of Curved Surfaces, editted with a new introduction and notes by Peter Pesic, Mineola, NY: Dover Publications, ISBN 978-0-486-44645-5.
• Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), Modern Differential Geometry of Curves And Surfaces With Mathematica®, Studies in Advanced Mathematics (3rd ed.), Boca Raton, FL: Chapman & Hall/CRC, ISBN 978-1-58488-448-4
• Han, Qing; Hong, Jia-Xing (2006), Isometric Embedding of Riemannian Manifolds in Euclidean Spaces, American Mathematical Society, ISBN 978-0-8218-4071-9
• Helgason, Sigurdur (1978), Differential Geometry，Lie Groups, and Symmetric Spaces, Academic Press, New York, ISBN 978-0-12-338460-7
• Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8
• Hitchin, Nigel (2013), Geometry of Surfaces (PDF)
• Hopf, Heinz (1989), Lectures on Differential Geometry in the Large, Lecture Notes in Mathematics, vol. 1000, Springer-Verlag, ISBN 978-3-540-51497-8
• Imayoshi, Y.; Taniguchi, M. (1992), An Introduction to Techmüller spaces, Springer-Verlag, ISBN 978-0-387-70088-5
• Ivey, Thomas A.; Landsberg, J.M. (2003), Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Systems, Graduate Studies in Mathematics, vol. 61, American Mathematical Society, ISBN 978-0-8218-3375-9
• Katz, Mikhail G. (2007), Systolic geometry and topology, Mathematical Surveys and Monographs, vol. 137, American Mathematical Society, ISBN 978-0-8218-4177-8
• Kobayashi, Shoshichi (1956), "Induced connections and imbedded Riemannian space", Nagoya Math. J., 10: 15–25, doi:10.1017/S0027763000000052
• Kobayashi, Shoshichi (1957), "Theory of connections", Annali di Matematica Pura ed Applicata, Series 4, 43: 119–194, doi:10.1007/BF02411907, S2CID 120972987,
• Kobayashi, Shoshichi; Nomizu, Katsumi (1963), Foundations of Differential Geometry, Vol. I, Wiley Interscience, ISBN 978-0-470-49648-0
• Kobayashi, Shoshichi; Nomizu, Katsumi (1969), Foundations of Differential Geometry, Vol. II, Wiley Interscience, ISBN 978-0-470-49648-0
• Kreyszig, Erwin (1991), Differential Geometry, Dover, ISBN 978-0-486-66721-8
• Kühnel, Wolfgang (2006), Differential Geometry: Curves - Surfaces - Manifolds, American Mathematical Society, ISBN 978-0-8218-3988-1
• Levi-Civita, Tullio (1917), "Nozione di parallelismo in una varietà qualunque", Rend. Circ. Mat. Palermo, 42: 173–205, doi:10.1007/BF03014898, S2CID 122088291
• O'Neill, Barrett (2006), Elementary Differential Geometry (revised 2nd ed.), Amsterdam: Elsevier/Academic Press, ISBN 0-12-088735-5
• Osgood, B.; Phillips, R.; Sarnak, P. (1988), "Extremals of determinants of Laplacians", J. Funct. Anal., 80: 148–211, doi:10.1016/0022-1236(88)90070-5
• Osserman, Robert (2002), A Survey of Minimal Surfaces, Dover, ISBN 978-0-486-49514-9
• Ian R. Porteous (2001) Geometric Differentiation: for the intelligence of curves and surfaces, Cambridge University Press ISBN 0-521-00264-8.
• Pressley, Andrew (2001), Elementary Differential Geometry, Springer Undergraduate Mathematics Series, Springer-Verlag, ISBN 978-1-85233-152-8
• Sacks, J.; Uhlenbeck, Karen (1981), "The existence of minimal immersions of 2-spheres", Ann. of Math., 112 (1): 1–24, doi:10.2307/1971131, JSTOR 1971131
• Singer, Isadore M.; Thorpe, John A. (1967), Lecture Notes on Elementary Topology and Geometry, Springer-Verlag, ISBN 978-0-387-90202-9
• Spivak, Michael (1965), Calculus on manifolds. A modern approach to classical theorems of advanced calculus, W. A. Benjamin
• Stillwell, John (1996), Sources of Hyperbolic Geometry, American Mathematical Society, ISBN 978-0-8218-0558-9
• Struik, Dirk (1987), A Concise History of Mathematics (4th ed.), Dover Publications, ISBN 0486602559
• Struik, Dirk J. (1988), Lectures on Classical Differential Geometry (reprint of 2nd ed.), New York: Dover Publications, Inc., ISBN 0-486-65609-8
• Taylor, Michael E. (1996a), Partial Differential Equations II: Qualitative Studies of Linear Equations, Springer-Verlag, ISBN 978-1-4419-7051-0
• Taylor, Michael E. (1996b), Partial Differential Equations III: Nonlinear equations, Springer-Verlag, ISBN 978-1-4419-7048-0
• Thorpe, John A. (1994), Elementary topics in differential geometry, Undergraduate Texts in Mathematics, Springer-Verlag, ISBN 0387903577
• Toponogov, Victor A. (2005), Differential Geometry of Curves and Surfaces: A Concise Guide, Springer-Verlag, ISBN 978-0-8176-4384-3
• Valiron, Georges (1986), The Classical Differential Geometry of Curves and Surfaces, Math Sci Press, ISBN 978-0-915692-39-2 Full text of book
• Warner, Frank W. (1983), Foundations of differentiable manifolds and Lie groups, Graduate Texts in Mathematics, vol. 94, Springer, ISBN 0-387-90894-3
• Wells, R. O. (2017), Differential and complex geometry: origins, abstractions and embeddings, Springer, ISBN 9783319581842
• Wilson, Pelham (2008), Curved Space: From Classical Geometries to Elementary Differential Geometry, Cambridge University Press, ISBN 978-0-521-71390-0

External links

• Media related to Differential geometry of surfaces at Wikimedia Commons