모둘리 공간

수학에서, 특히 대수 기하학에서, 모듈리 공간은 기하학적 공간(대개 체계 또는 대수적 스택)이며, 점들은 어떤 고정된 종류의 알헤브로-기하학적 객체 또는 그러한 물체의 이소모르피즘 클래스를 나타낸다. 이러한 공간은 분류 문제의 해결책으로 자주 발생한다. 만일 흥미로운 물체의 집합(예를 들어 고정된 속물의 부드러운 대수 곡선)이 기하학적 공간의 구조를 부여할 수 있다는 것을 보여줄 수 있다면, 그 결과 공간에 좌표를 도입하여 그러한 물체를 파라메트리할 수 있다. 이 맥락에서 "modulus"라는 용어는 "parameter"와 동의어로 사용된다. moduli 공간은 처음에는 물체의 공간이 아닌 매개변수의 공간으로 이해되었다. 모듈리 공간의 변형으로는 형식적인 모듈리가 있다.

동기

모둘리 공간은 기하학적 분류 문제 해결의 공간이다. 즉, 모듈리 공간의 점은 기하학적 문제의 해법에 해당한다. 여기서 서로 다른 해결책이 이형성(즉, 기하학적으로 동일)인 경우 식별된다. 모둘리 공간은 문제에 대한 매개 변수의 보편적인 공간을 주는 것으로 생각할 수 있다. 예를 들어 유클리드 평면에서 모든 원을 일치시킬 때까지 찾아내는 문제를 고려하십시오. 어떤 원이라도 3점을 주어 독특하게 묘사할 수 있지만, 많은 다른 세트의 3점은 같은 원을 준다. 즉, 서신은 다대1이다. 그러나 원은 중심과 반경을 주어 독특하게 매개변수화된다. 즉, 두 개의 실제 매개변수와 한 개의 양의 실제 매개변수다. 우리는 원에만 관심이 있기 때문에 중심은 다르지만 반지름은 같은 원들을 식별하고, 반지름만으로도 관심의 집합을 매개변수화하기에 충분하다. 따라서 모듈리 공간은 양의 실수다.

모둘리 공간은 종종 자연적인 기하학적 구조와 위상학적 구조도 지니고 있다. 예를 들어 원의 예에서 모듈리 공간은 단순한 추상적인 집합이 아니라, 반지름 차이의 절대값은 두 원이 "가까이" 있는 때를 결정하기 위한 메트릭을 정의한다. 모듈리 공간의 기하학적 구조는 기하학적 분류 문제의 두 해법이 '닫힐 때'를 알려 주지만, 일반적으로 모듈리 공간 역시 복잡한 지구 구조를 가지고 있다.

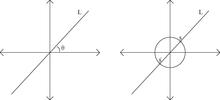
예를 들어, 원점을 교차하는 R의² 선 모음을 설명하는 방법을 생각해 보십시오. 우리는 이 가족의 각 L라인에 그것을 고유하게 식별할 수 있는 수량인 계수를 할당하고 싶다. 그러한 수량의 예는 0 ≤ < rad 라디안의 양각 θ(L)이다. 그렇게 파라메타된 L 선 세트를 P¹(R)라고 하며 실제 투영 선이라고 한다.

위상학적 구조를 이용하여 원점을 교차하는 R의² 선들의 집합도 설명할 수 있다. To wit: S¹ ⊂ R을² 고려하고 모든 점 s ∈ S는¹ (원점과 s를 결합하는) 집합에서 L(s)을 제공한다는 점에 주목한다. 단, 이 지도가 2대 1이므로 이 공간의 위상이 지수 지도 S¹ → P(R¹)에 의해 유도된 지수 위상인 P¹(R) ≅ S¹/~를 산출하기 위해 s ~s를 식별하고자 한다.

따라서 우리가¹ P(R)를² R에서 기원을 교차하는 선의 모듈리 공간으로 고려할 때, 우리는 가족의 구성원(이 경우 선)이 지속적으로 0 ≤ θ < π)을 변화시킴으로써 변조할 수 있는 방법을 포착한다.

기본 예시

투영 공간과 그라스만인

실제 투사 공간 P는ⁿ 원점을 통과하는 R의ⁿ⁺¹ 선의 공간을 파라메트리하는 모듈리 공간이다. 마찬가지로 복잡한 투영 공간은 C의ⁿ⁺¹ 모든 복합 선들이 원점을 통과하는 공간이다.

보다 일반적으로 필드 F 위에 있는 벡터 공간 V의 그래스만 G(k, V)는 V의 모든 k차원 선형 서브스페이스의 모듈리 공간이다.

전지구적으로 생성된 섹션이 있는 매우 풍성한 선다발의 투영 공간

이야기가 중단될 때마다 X가 보편적인 사영 공간에{X\displaystyle}계획을 PZn(_{\mathbb{Z}}^{n}읬던 1가지 이슈 때문이었습니다}은 ,[1][2]은던 1가지 이슈 때문이었습니다 한줄 다발에 의해서 주어진다 L→ X{\displaystyle{{나는\mathcal}}\to X}과 n+1{\displaystyle n+1}부분 s0,…, sn.∈${\displaystyle \mathrm{\gamma }(X}$, ${\displaystyle L}$) ${\displaystyle s_{0},\ldots ,s_{n}\in \Gamma(X$, ${\mathcal{L})$ 모두$$ 동시에 사라지지 않는 \Displaysty s_{0}, \dots_s_{n}\}\in}. 이 말은, 요점이 주어진다는 뜻이다.

${\displaystyle x:{\text{Spec}(R)\to X}$

관련점이 있다.

${\displaystyle {\hat {x}:{\text{Spec}(R)\to \mathbf {P} _{\mathb {Z}^{n}}}}}}}$

작문대로 주어지는

${\displaystyle [s_{0}:\cdots :s_{n}]\cdcots :s_{n}(x)]\in \mathbf {P} _{\mathb {Z}^{n}(R)}$

그런 다음, 섹션이 있는 두 개의 라인 번들이 동일하다.

${\displaystyle({\mathcal {L},(s_{0},\ldots,s_{n})\심({\mathcal {L}),(s_{0}),\ldots ,s_{n})}}}}$

$if{\displaystyle }$ orph ($s{\displaystyle }$ i${\displaystyle }$)${\displaystyle }$= ${\displaystyle {}_{}^{}}$ ${\displaystyle i_{}^{}}$ = s$_ (s_{i}=s_{$i}'})와 같은 이소모르프 ism ${\displaystyle \{\backslash }$$displaystyle \pi$$:{$pi}{\$mathcal {L}}}}$이(가) 있는 경우$.$ 이는 관련 모듈리 펑터를 의미한다.

${\displaystyle \mathbf {P} _{\mathb {Z}}^{n}:{\text{Sch}\to {\text{세트}}$

구성표 $X{\displaystyle }$ ${\displaystyle X}$을(를) 세트로$$ 전송

${\displaystyle \mathbf {P} _{\mathb {Z}^{n}(X)=\left\{\({\mathcal {L},s_{0},\ldots ,s_{n}):{\begin{matrix}{\mathcal{L}\to X{{\text}는 선다발}\\\ldots,s_{n}\in \Gamma(X, {\mathcal {L})\\\\text{\text}}\}}}\{matrix\sim}} 글로벌 섹션의 기초를 형성한다.$

Showing this is true can be done by running through a series of tautologies: any projective embedding ${\displaystyle i:X\to \mathbb {P} _{\mathbb {Z} }^{n}}$ gives the globally generated sheaf ${\displaystyle i^{*}{\mathcal {O}}_{\mathbf {P} _{\mathbb {Z} }^{n}}(1)}$ with 섹션 $i{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}{}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ x ${\displaystyle n_{}}$ ${\$ i$^{*}x_{0},\ldots,$${\displaystyle i}$$^{*}x_{n$ 반대로 $n{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle$ ${\mathcal$$}\}\to$ $X}$에 충분한 $선다발$이 주어지면 $위$와 같이 임베딩이 된다${\displaystyle .}$

차우 버라이어티

차우 버라이어티 차우(d,P³)는 P에서³ parametries d curve를 parametries로 하는 투영 대수적 품종이다. 그것은 다음과 같이 구성된다. C를 P의³ 도 d의 곡선이 되게 한 다음, C 곡선과 교차하는 P의³ 모든 선을 고려한다. 이것은 G(2, 4)의 D등분자_C, P의³ 선들의 Grassmannian이다. C가 변화할 때, C와 D를_C 연관시킴으로써, 우리는 Grassmannian의 d d d d divisor 공간의 부분집합으로서 d 도 곡선의 매개변수 공간을 얻는다. 차우(d,P³)

힐버트 계획

힐베르트 체계 힐브(X)는 모듈리 체계다. 힐브(X)의 모든 폐쇄점은 고정 체계 X의 폐쇄 하위 체계에 해당하며, 모든 폐쇄 하위 체제는 그러한 점으로 표현된다. 힐버트 체계의 간단한 예는 투사 공간 $P{\displaystyle {\mathbb{}}^{}}$ ${\$$displaystyle$ d$}$과(와)의 Hilbert scheme parameterizing d ${\$$displaystyle \mathb{P} ^{n}}}}}$ 과(과$$)이다$.$ 이것은 투영 번들에 의해 주어진다.

${\displaystyle {\mathcal {Hilb}_{d}(\mathb {P}^{n}=\Mathb {P})(\Gamma({\mathcal {O})(d))}}$

에 의해 주어지는 보편적인 가족으로.

${\displaystyle {\mathcal {U}=\{(V(f),f):f\in \Gamma({\mathcal {O}(d))\}}$

여기서 $V{\displaystyle }$(${\displaystyle f}$) ${\displaystyle V(f)}$은 $d{\displaystyle }$ ${\displaystyle d}$ 동종$$ 다항식 $f{\displaystyle }$ ${\displaystyle f}$의 관련 투영 체계다$.$

정의들

우리가 모둘리 공간이라고 부를 수 있는 몇 가지 관련 개념들이 있다. 이러한 각각의 정의는 공간 M의 점들이 기하학적 물체를 나타내는 것을 의미하는 다른 개념을 공식화한다.

미세한 모듈리 공간

이것이 표준 개념이다. Heuristically, if we have a space M for which each point m ∊ M corresponds to an algebro-geometric object U_m, then we can assemble these objects into a tautological family U over M. (For example, the Grassmannian G(k, V) carries a rank k bundle whose fiber at any point [L] ∊ G(k, V) is simply the linear subspace L ⊂ V.) M is called a base space of 가족 U. 우리는 그러한 가족이 보편적이라고 말한다. 만약 어떤 기본 공간 B에 대한 알헤브로-기하학적 물체 T의 가족이 U의 풀백이라면 독특한 지도 B → M. 미세한 모둘리 공간은 보편적 가족의 기반인 공간 M이다.

더 정확히 말하자면, 우리가 계획에서 집합까지 functor F를 가지고 있다고 가정해보자. 이 Functor F는 기본 B가 있는 모든 적절한 개체군의 집합을 체계 B에 할당한다. Space M은 M이 F를 나타내는 경우 F f를 위한 미세한 모듈리 공간이다. 즉, Hom(-, M)이 포인트의 functor인 자연 이형성 τ : F → Hom(-, M)이 있다. 이것은 M이 보편적인 가족을 가지고 있다는 것을 암시한다; 이 가족은 ID 지도 1_M ∊ Hom(M, M)에 해당하는 M의 가족이다.

거친 모듈리 공간

미세한 모듈리 공간은 바람직하지만, 항상 존재하는 것은 아니며 종종 구성하기 어려운 공간이기 때문에 수학자들은 때때로 거친 모듈리 공간의 개념인 약한 개념을 사용한다. Space M은 자연적 변환이 존재한다면 functor F를 위한 거친 모듈리 공간이다. natural : F → Hom(-, M)과 τ은 그러한 자연 변형 중에서 보편적이다. 좀 더 구체적으로 말하면, M은 기초 B 위에 있는 어떤 패밀리 T가 φ_T : B → M을 발생시키고, V와 W가 이형인 경우에만 동일한 M 지점에 해당하는 경우 F를 위한 거친 모듈리 공간이다. 따라서 M은 한 패밀리에 나타날 수 있는 모든 사물에 대한 지점이 있는 공간이며, 그 기하학에는 패밀리에 따라 사물이 달라질 수 있는 방법이 반영되어 있다. 그러나, 거친 모듈리 공간은 보편적인 것은 말할 것도 없고, 반드시 적절한 물체의 어떤 제품군도 운반하지 않는다는 점에 유의한다.

즉, 미세한 모듈리 공간은 베이스 공간 M과 유니버설 패밀리 U → M을 모두 포함하는 반면, 거친 모듈리 공간은 베이스 공간 M만을 가지고 있다.

모둘리 스택

흥미로운 기하학적 물체들이 자연 자동화를 많이 갖춘 경우가 많다. 이것은 특히 미세한 모듈리 공간의 존재를 불가능하게 만든다(직관적으로 L이 어떤 기하학적 물체라면, 사소한 가족 L × [0,1]은 비경쟁적 자동형태를 통해 L × {1}과 L × {0}을(를) 확인함으로써 원 S의¹ 뒤틀린 가족으로 만들 수 있다는 생각이다. 이제 미세한 모듈리 공간 X가 존재한다면, 지도¹ S → X는 일정한 것이 아니라, 사소한 것에 의한 적절한 오픈 세트에 일정해야 할 것이다), 여전히 때로는 거친 모듈리 공간을 얻을 수 있다. 그러나 이러한 접근법은 이상적인 것이 아니다. 그러한 공간은 존재한다고 보장되지 않으며, 그러한 공간은 존재할 때 종종 단수적이며, 그들이 분류하는 일부 비독점적 개체군에 대한 세부사항을 놓치기 때문이다.

보다 정교한 접근방식은 이형성을 기억함으로써 분류를 풍부하게 하는 것이다. 더 정확히 말하면, 어떤 기초에서든, B에 있는 가족의 범주는 형태론으로 간주될 수 있다. 그런 다음 어떤 공간 B에 할당되는 섬유질 범주를 B 이상의 가족 집단으로 간주한다. 모듈리 문제를 설명하기 위해 그룹오이드에 있는 이러한 범주의 사용은 그로텐디크(1960/61)로 거슬러 올라간다. 일반적으로는 계략이나 대수적 공간으로도 나타낼 수 없지만, 많은 경우 대수적 스택의 자연 구조를 가지고 있다.

Deligne-Mumford(1969년)에서는 주어진 속 곡선의 (코리큘리) 모듈리 공간의 무reducibility를 증명하기 위한 도구로서 대수적 스택과 모듈리 문제를 분석하기 위한 사용이 나타났다. 대수적 스택의 언어는 본질적으로 모듈리 문제를 구성하는 섬유화된 범주를 "공간"으로 볼 수 있는 체계적 방법을 제공하며, 많은 모듈리 문제의 모듈리 스택은 해당 거친 모듈리 공간보다 더 행동(매끄러운 것 등)이 좋다.

추가 예

곡선모듈리

moduli stack $M{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle g_{}}$ ${\$은 g의 부드러운 투영 곡선 패밀리와 그 이형성을 분류한다$$. g > 1일 때, 이 스택은 안정적인 결절 곡선에 해당하는 새로운 "경계" 포인트를 추가함으로써 압축될 수 있다(이형성과 함께). 곡선은 한정된 자동화 그룹만 가지고 있다면 안정적이다. 결과 스택은 $M$의${\displaystyle {\stackrel{}{}g}_{}}$ ${\$로 표시되며$,$ 두 모듈리 스택 모두 곡선의 범용 패밀리를 운반한다. 또한 부드럽고 안정적인 곡선의 이형성 등급을 나타내는 거친 모듈리 공간을 정의할 수 있다. 이 거친 모듈리 공간들은 모듈리 스택의 개념이 발명되기 전에 실제로 연구되었다. 사실, 모듈리 스택의 개념은 Deligne와 Mumford에 의해 거친 모듈리 공간의 투영성을 증명하기 위한 시도로 발명되었다. 최근 몇 년 동안, 곡선의 스택이 실제로 더 근본적인 물체라는 것이 명백해졌다.

위의 두 스택 모두 치수 3g-3이 있으므로 g > 1일 때 3g-3 매개변수 값을 선택하여 안정적인 결절 곡선을 완전히 지정할 수 있다. 하위 속에서는 개수를 빼서 매끄러운 자동화 계열의 존재를 설명해야 한다. 0속, 리만 구체의 복잡한 곡선이 정확히 하나 있으며, 그 집단은 PGL(2)이다. 따라서 $M{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle 0_{\mathrm{}}}$ ${\$의 치수는 다음과 같다$$.

딤(속 0 곡선의 공간) - 딤(자동화 그룹) = 0 - 딤(PGL (2)) = -3.

마찬가지로 제1속에서도 곡선의 1차원 공간이 존재하지만, 그러한 곡선마다 1차원 자동화 그룹이 있다. 따라서 스택 $M{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle 1_{\mathrm{}}}$ ${\$1}의 치수는 0이다$$. 거친 모듈리 공간은 g > 1이 있는 곡선은 그 자동형성으로서 유한군만을 가지기 때문에 g > 1이 되면 치수 3g-3이 쌓인다. 즉, 딤(자동화 그룹) = 0. 결국 속 0에서는 거친 모듈리 공간은 치수 0을 가지며, 1은 치수 1을 가지기 때문이다.

또한 n개의 표시된 점이 있는 g노달 곡선의 모듈리 스택을 고려함으로써 문제를 풍부하게 할 수 있다. 이러한 표시 곡선은 표시점을 고정하는 곡선 자동화의 부분군이 유한하면 안정적이라고 한다. n-표시가 없는 부드러운(또는 안정적인) 속 g 곡선의 결과 모듈리 $스택$은 ${\displaystyle M_{}}$g , ${\displaystyle n_{}}${\$displaystyle${\$mathcal{M}_{g,n$}($$${\displaystyle {\mathrm{또는}}_{}}$ M${\displaystyle {\stackrel{}{}}_{\},}}$ ${\${\\\$mathcal{M}}}_{g,n})$으로 표시되며 치수는 3g - 3+n이다.

특히 관심 있는 사례는 모듈리 스택 $M{\displaystyle {\stackrel{}{\mathcal{}}1}_{\mathrm{}}}$,${\displaystyle 1_{}}$ ${\$ 1개의 표시점을 가진 1개 속 곡선의 모듈리$$ 스택이다. 이것은 타원형 곡선의 스택이며, 이 스택에 있는 다발의 용적형 섹션인, 많이 연구된 모듈형 형태의 자연 서식지다.

품종모둘리

더 높은 차원에서는 대수적 품종의 모듈리를 구성하고 연구하기가 더 어렵다. 예를 들어 위에서 논의한 타원곡선의 모듈리 공간의 고차원 아날로그는 시겔 모듈러 품종과 같은 아벨리아 품종의 모듈리 공간이다. 이것이 Sigel 모듈형 이론의 기초가 되는 문제다. 시무라 품종을 참조하십시오.

벡터 번들의 모둘리

또 다른 중요한 모듈리 문제는 고정 대수적 다양성 X에 순위 n 벡터 번들의 모듈리 스택 벡트_n(X)의 기하학을 이해하는 것이다.^[3] 이 스택은 X가 1차원일 때, 특히 n이 1일 때 가장 많이 연구되었다. 이 경우 거친 모듈리 공간은 곡선의 모듈리 공간과 마찬가지로 스택이 발명되기 전에 연구된 피카르드 구조다. 다발이 1등과 0등일 때, 거친 모둘리 공간에 대한 연구는 야코비안 품종을 연구하는 학문이다.

물리학 응용에서 벡터 번들의 모듈리의 수와 주요 G번들의 모듈리의 숫자의 밀접하게 관련된 문제가 게이지 이론에서 유의미한 것으로 밝혀졌다.^{[citation needed]}

모듈리 공간의 볼륨

리만 표면과 접해 있는 모듈리 공간의 간단한 지질학 및 Weil-Petersson 볼륨.

모듈리 공간 구성 방법

모듈리 문제의 현대적 공식화 및 모듈리 공간의 정의는 모듈리 펑커(또는 보다 일반적으로 그룹로이드에서 섬유화되는 범주)와 이들을 대표하는 공간(대부분)의 측면에서 모듈리 공간의 정의와 이를 나타내는 것으로, 그가 복잡한 테히뮐러 공간을 이용한 일반적인 틀, 접근법 및 주요 문제를 기술한 그로텐디크(1960/61)로 거슬러 올라간다. 해석 기하학을 예로 들어보자. 특히 이번 회담에서는 우선 고려 중인 모듈리 문제를 경직시켜 모듈리 공간을 구축하는 일반적인 방법을 기술하고 있다.

더 정확히 말하면, 분류되는 물체의 비경쟁 자동화가 존재하기 때문에 미세한 모듈리 공간을 가질 수 없게 된다. 그러나 종종 추가 데이터를 존중하는 유일한 자동화 방식으로 선택되는 추가 데이터와 함께 원본 객체를 분류하는 수정된 모듈리 문제를 고려할 수 있다. 경화 데이터의 적절한 선택으로, 수정된 모듈리 문제는 종종 적절한 힐버트 체계 또는 인용 체계에서 하위 체임으로 설명되는 (미세) 모듈리 공간 T를 갖게 될 것이다. 또한 강체화 데이터는 대수 구조 그룹 G가 있는 주요 번들에 해당하도록 선택된다. 따라서 G의 작용에 의해 지수를 취함으로써 경직된 문제에서 원점으로 되돌아갈 수 있으며, 모듈리 공간을 구성하는 문제는 G의 작용에 의해 T의 지수를 (적당하게 강한 의미에서는) T의 지수를 갖는 계략(또는 더 일반적인 공간)을 찾는 문제가 된다. 일반적으로 마지막 문제는 해결책을 인정하지 않지만, 적절한 조건 하에서 그 지수가 실제로 존재한다는 것을 보여주는 데이비드 뭄포드가 1965년에 개발한 획기적인 기하불변성 이론(GIT)에 의해 다루어진다.

이것이 어떻게 작용하는지 보려면, 속 g > 2의 매끄러운 곡선을 파라메트리징하는 문제를 고려하라. 도 d > 2g의 완전한 선형 시스템과 함께 매끄러운 곡선은 투사 공간^d−g P의 닫힌 1차원 하위 체임과 같다. 따라서 부드러운 곡선과 선형 시스템의 모듈리 공간(특정 기준을 만족함)은 충분히 고차원 투영 공간의 힐버트 계획에 포함될 수 있다. 힐버트 체계에서 이 위치 H는 선형 시스템의 요소들을 혼합하는 PGL(n)의 작용을 가지고 있다. 결과적으로, 부드러운 곡선의 모듈리 공간은 투영적인 일반 선형 그룹에 의해 H의 몫으로 회복된다.

또 다른 일반적인 접근법은 주로 마이클 아틴과 관련이 있다. 여기서 그 생각은 분류할 종류의 물체로부터 시작하여 그것의 변형 이론을 연구하는 것이다. 이것은 우선 극미량의 변형을 만든 다음, 공식 베이스 위에 이것들을 하나의 물체로 조립하기 위한 표현가능성 이론에 호소한다는 것을 의미한다. 다음으로, 그로텐디크의 형식적 존재 정리에 대한 어필은 완전한 국부적인 고리인 베이스 위에 원하는 종류의 물체를 제공한다. 이 물체는 미세하게 생성된 링 위에 정의된 물체에 의해 Artin의 근사 정리를 통해 근사치를 구할 수 있다. 이 후자의 링의 스펙트럼은 원하는 모듈리 공간에 일종의 좌표도를 제공하는 것으로 볼 수 있다. 이 차트를 충분히 붙이면 공간을 커버할 수 있지만, 우리의 스펙트럼 조합에서 모듈리 공간까지의 지도는 대체로 1대 1이 될 것이다. 따라서 우리는 전자에 대해 동등성 관계를 정의한다. 본질적으로, 두 점은 각각 위의 물체가 이형성인 경우 동등하다. 이것은 계략과 등가 관계를 주는데, 이는 항상 계략이 아니더라도 대수적 공간(실제로 우리가 조심하고 있다면 대수적 스택)을 정의하기에 충분하다.

물리학에서는

moduli space라는 용어는 특히 스칼라 필드 집합의 진공 기대값의 moduli space 또는 가능한 문자열 배경의 moduli space를 지칭하기 위해 물리학에 사용된다.

모둘리 공간은 위상학 분야 이론에서도 물리학에서 나타나는데, 파인만 경로 통합을 이용하여 다양한 대수적 모둘리 공간의 교차점 수를 계산할 수 있다.

참고 항목

건설공구

• 힐버트 계획
• 인용구획정
• 변형 이론
• GIT 지수
• Artin의 기준, moduli functors에서 대수적 스택으로 moduli 공간을 구성하기 위한 일반 기준

모둘리 공간

• 대수곡선의 모둘리
• 타원곡선의 모듈리 스택
• 모듈 곡선
• 피카르 펑터
• 반음절단 곡선모듈리
• 콘체비치 모둘리 공간
• 반음절단 모둘리

참조

메모들

• 모둘리 이론
• P-adic 모듈형 및 Langlands 프로그램의 모듈형 스택

연구기사

기초 논문

• Grothendieck, Alexander (1960–1961). "Techniques de construction en géométrie analytique. I. Description axiomatique de l'espace de Teichmüller et de ses variantes" (PDF). Séminaire Henri Cartan 13 No. 1, Exposés No. 7 and 8. Paris.

• Mumford, David, 기하학적 불변 이론. Ergebnisse der Mathik under Ihrer Grenzgebiete, Neue Polge, 밴드 34 Springer-Verlag, 1965-New York vi+145 MR0214602
• Mumford, David, Forgarty, J., Kirwan, F. 기하학적 불변 이론. 제3판. 에르헤비니스 데르 메틸리크(Ergebnisse der Mathalik)와 이헤러 그렌즈게비엣(2) (수학과 관련 영역의 결과 (2)), 34. 베를린 스프링거-베를라크, 1994. 시브+292 페이지 MR1304906 ISBN 3-540-56963-4

초기 애플리케이션

• Deligne, Pierre; Mumford, David (1969). "The irreducibility of the space of curves of given genus" (PDF). Publications Mathématiques de l'IHÉS. 36: 75–109. CiteSeerX 10.1.1.589.288. doi:10.1007/bf02684599.
• Faltings, Gerd; Chai, Ching-Li (1990). Degeneration of Abelian Varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete. Vol. 22. With an appendix by David Mumford. Berlin: Springer-Verlag. doi:10.1007/978-3-662-02632-8. ISBN 978-3-540-52015-3. MR 1083353.
• Katz, Nicholas M; Mazur, Barry (1985). Arithmetic Moduli of Elliptic Curves. Annals of Mathematics Studies. Vol. 108. Princeton University Press. ISBN 978-0-691-08352-0. MR 0772569.

기타 참조

• 파파도풀로스, 아타나세, 에드(2007), 타이히뮐러 이론 핸드북. 수학과 이론물리학 IRMA 강의, 11, 유럽수학학회(EMS), 취리히(Zürich), 도이:10.4171/029, ISBN 978-3-03719-029-6, MR2284826
• 파파도풀로스, 아타나세, 에드(2009년), 타이히뮐러 이론 핸드북. 제2권, 수학과 이론물리학 IRMA 강의, 13, 유럽수학학회(EMS), 취리히, 도이:10.4171/055, ISBN 978-3-03719-055-5, MR2524085
• 파파도풀로스, 아타나세, 에드(2012), 타이히뮐러 이론 핸드북. Vol. III, IRMA 수학과 이론 물리학 강의, 17, 유럽수학학회(EMS), 취리히, 도이:10.4171/103, ISBN 978-3-03719-103-3.

기타 물품 및 출처

• Harris, Joe; Morrison, Ian (1998). Moduli of Curves. Graduate Texts in Mathematics. Vol. 187. New York: Springer Verlag. doi:10.1007/b98867. ISBN 978-0-387-98429-2. MR 1631825.

• Viehweg, Eckart (1995). Quasi-Projective Moduli for Polarized Manifolds (PDF). Springer Verlag. ISBN 978-3-540-59255-6.

• Simpson, Carlos (1994). "Moduli of representations of the fundamental group of a smooth projective variety I" (PDF). Publications Mathématiques de l'IHÉS. 79: 47–129. doi:10.1007/bf02698887.
• Maryam Mirzakhani(2007) "간단한 지질학 및 Weil-Petersson의 리만 표면 모듈리 공간의 볼륨" 수학 발명

외부 링크

• Lurie, J. (2011). "Moduli Problems for Ring Spectra". Proceedings of the International Congress of Mathematicians 2010 (ICM 2010). pp. 1099–1125. doi:10.1142/9789814324359_0088.