기본 다각형

수학에서, 0보다 큰 속들의 모든 콤팩트 리만 표면에 대해 기본적인 폴리곤을 정의할 수 있다.그것은 그것의 기본 집단을 통해 표면의 위상뿐만 아니라 리만 표면의 일치성까지 결정한다.균일화 정리에 의해, 모든 콤팩트 리만 표면은 정확히 다음 중 하나에 의해 주어진 범용 피복 표면을 간단히 연결했다.

• 리만 구,
• 복잡한 비행기,
• 단위 디스크 D 또는 동등하게 상부 하프 평면 H.

0종의 첫 번째 경우 표면은 리만 구와 일치한다.

두 번째 속 1의 경우, 표면은 C의 일부 격자 Ⅱ에 대한 토러스 C/λ과 일치하게 동등하다.conve의 기본 다각형은, 볼록하다고 가정할 경우, 주기 평행도 또는 중심 대칭 육각형 중 하나로 간주할 수 있으며, 그 결과는 1891년 Fedorov에 의해 처음 입증되었다.

속 g > 1의 마지막 경우, 리만 표면은 일치하게 H/γ과 동등하며, 여기서 γ은 뫼비우스 변환의 후치안 그룹이다.γ의 기본 영역은 H의 쌍곡선 메트릭에 대한 볼록 폴리곤에 의해 주어진다.이것들은 디리클레 폴리곤에 의해 정의될 수 있고 짝수의 면을 가지고 있다.기본 그룹 γ의 구조는 그러한 다각형에서 판독할 수 있다.quasiconformal 매핑과 벨트 라미 방정식 이론을 이용하여, 그곳요 4g는 측면과 Γ의 단체로 표준 발표회에 등 발전기에 해당하는 정준 볼록 디리클레 다각형, 먼저 Fricke로 정의된, b1, a2, b2, a1..., 농업, bgs자루. 및 단일 관계[a1,b1][a2,b2]⋅⋅⋅[ag,bg]=1,-LSB- a이 나타날 수 있,b 해결을-1ba−1b⁻¹.

지향적인 폐쇄형 2-manifold M의 리만 미터법은 M에 복잡한 구조를 정의하여 M을 콤팩트한 리만 표면으로 만든다.Through the use of fundamental polygons, it follows that two oriented closed 2-manifolds are classified by their genus, that is half the rank of the Abelian group Γ/[Γ,Γ], where Γ = π₁(M). Moreover, it also follows from the theory of quasiconformal mappings that two compact Riemann surfaces are diffeomorphic if and only if they are homeomorphic.결과적으로, 두 개의 폐쇄 지향적인 2-매니폴드는 차이점형인 경우에만 동형이다.그러한 결과는 또한 미분 위상 방법을 사용하여 증명될 수 있다.^[1][2]

속 1의 기본 다각형

병렬형 문자 및 중심 대칭 16진수

로사의 경우 근본적인 볼록 다각형 행동을 위해 Λ의 번역에 의해 만약이 Λ)Z2)Z+Z거야. 유개념 한 리만 표면의 양식 Λ 것으로 볼 수 있다)Z2필요한 ZR2=C가 a와 b선형적으로 R에(R2에 실질적인 선형 변환을 수행한 후 독립에 대한⊕ Zb, 그것을 가정할 수 있고 있다.)Z+ Z Ω, 임 Ω > 0.) 기본 영역은 0 < 초 >, t < 1에 대해 평행사변형 s x + t y로 주어지며, 여기서 x와 y는 generators의 생성자다.

C가 기본 볼록 폴리곤의 내부인 경우, X로서 C + x 커버 R을² λ 위로 이동시킨다.C의 경계점은 C ∩ (C + x) 교차로에 형성되어 있다.이것들은 ∂C의 콤팩트 볼록 세트로서, 따라서 C의 정점이나 C의 측면 중 하나이다.C의 모든 닫힌 면은 이렇게 쓰여질 수 있다.-x로 번역하면 C ∩(C - x)도 C의 한 면이라는 것을 따른다.따라서 C의 옆면은 길이가 같은 평행한 쌍으로 발생한다.길이가 같은 두 개의 병렬 세그먼트의 끝점은 교차하도록 결합될 수 있으며 교차점은 끝점을 연결하는 선 세그먼트의 중간점에서 발생한다.그러한 부문들의 교차점은 같은 지점에서 발생한다.그 점을 원점으로 번역하면, 폴리곤이 중심적으로 대칭적이라는 것을 따른다. 즉, 포인트 z가 폴리곤 안에 있으면 -z도 마찬가지다.

중심 대칭 볼록한 육각형 테셀레이트의 해석을 쉽게 볼 수 있다.A가 육각형 점인 경우 변위 벡터 AB와 AC에 의해 격자가 생성되며, 여기서 B와 C는 A의 인접하지 않고 A의 반대쪽이 아닌 두 정점이다.실제로 두 번째 그림은 AB와 AC 세그먼트에서 잘린 두 개의 삼각형을 치환하여 얻은 평행사변형과 육각형이 어떻게 동등한지를 보여준다.마찬가지로 첫 번째 그림도 6각형 타일링과 병렬로 타일링을 매칭하는 다른 방법을 보여준다.육각의 중심이 0이고 정점이 a, b, c, -a, -b, -c인 경우, λ은 발전기 a와 b + c를 가진 아벨 그룹이다.

Paralogram에 의해 생성된 기본 다각형의 예

여러 가지 방법으로 평행사변형의 측면을 식별하여 생성할 수 있는 위상은 정확히 네 가지(아래 사각형으로 표시됨)가 있다.

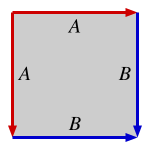구[3]

실제 투영면

클라인 병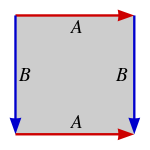

토러스

• 구체: ${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\$ 또는$$ $A{\displaystyle }$ ${\displaystyle B{}^{}}$- ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{}^{}}$- ${\displaystyle 1^{}}$ ${\$}:{-1$}$
• 실제 투영 평면:${\displaystyle A}$ ${\displaystyle AA}$ 또는$$ $A{\displaystyle }$ ${\displaystyle B}$ ${\displaystyle \mathrm{AB}}$ ${\displaystyle AB$$AB}$
• 클라인 병:${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\$ 또는$$ $A{\displaystyle }$ ${\displaystyle A}$ ${\displaystyle B}$ B ${\displaystyle AABB}$
• Torus: ${\displaystyle A}$ ${\displaystyle {}^{}}$A - ${\displaystyle 1^{}}$B - 1 ${\$1}B^{-$1$$}$ ${\displaystyle \mathrm{또는<img\; alt="ABA^\{-1\}B^\{-1\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/c6caa444b9e9549d0ae674d9805da32d35f3993f"\; style="vertical-align:\; -0.338ex;\; width:11.68ex;\; height:2.676ex;"\; papago-attr-id="63">}{}^{}}$ ${\displaystyle {\mathrm{B}}^{}}$ C${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\displaystyle {}^{}{}^{}}$- 1 C -$$ {\$displaysty$ABCA^{-$1}B$^{-1$}C$^{-1$}:{-1}}$

페도로프의 정리

1891년 러시아의 결정학자 에브그라프 페도로프가 제정한 페도로프의 정리는 평행사변형과 중앙 대칭 육각형만이 기본 영역인 볼록형 폴리곤이라고 단언한다.^[4]이것에 대한 몇 가지 증거가 있는데, 보다 최근의 것 중에는 볼록성 이론, 숫자의 기하학, 그리고 브룬-밍코프스키 불평등과 같은 원 패킹과 관련된 것들도 있다.^[5]H. S. M. Coxeter와 Voronoi로 인한 두 가지 기본적인 증거가 여기에서 제시될 것이다.^[6][7]

Coxeter의 증거는 2m 면이 있는 중앙 대칭 볼록 폴리곤 C가 있다고 가정하여 진행된다.그런 다음 N 기본² 평행그램으로 형성된 큰 폐쇄 평행그램은 큰 평행그램의 가장자리를 벗어나는 C의 번역에 의해 타일링된다.이로 인해 토러스 C/NNNT에 타일링이 유발된다. v, e 및 f를 이 타일링의 정점, 가장자리 및 면(인분 공간의 식별을 고려)으로 한다.그렇다면 토러스(torus)의 오일러-푸앵카레 특성은 0이기 때문에

${\displaystyle v-e+f=0.}$

반면에, 각 정점은 적어도 3개의 다른 가장자리에 있고 모든 가장자리는 두 개의 꼭지점 사이에 있기 때문에,

$3v\leq 2e}$

게다가 모든 가장자리는 정확히 두 면에 있기 때문에

$2mf.}$

그러므로

$(\displaystyle mf=e\leq 3(e-v)=3f.}$

하도록

$디스플레이 스타일 m\leq 3,}$

필요에 따라

보로노이의 증거는 C의 모든 가장자리가 λ의 원소 x에 해당한다는 관찰로부터 시작된다.사실 가장자리는 0에서 x까지의 반지름의 직교 이등분선이다.따라서 0에서 각 가장자리로 수직인 발은 각 가장자리의 내부에 위치한다.y가 격자점일 경우 1/2y는 C에 있을 수 없으며, 그럴 경우 –1/2y도 C에 있을 수 있으므로 C가 λ의 기본 영역이라는 것과 모순된다.±x₁, ..., ±x를_m C의 변에 해당하는 λ의 2m 구별 지점으로 한다.발전기 a와 b의 λ을 고정한다.따라서 x_i = α_i a + β_i b, 여기서 α와_i β는_i 정수다.그렇지 않으면 ± 1/2 x가_i 측면의 λ 지점일 것이므로 α와_i β_i 둘 다 균일할 수 없으며, 이는 C가 기본 영역인 것과 모순된다.따라서 정수 쌍(α_i, β_i) 모듈로 2: (0,1), (1,0), (1,1)에 대한 세 가지 가능성이 있다.따라서 m > 3일 경우, x_i - x_j 짝수, 즉 1/2 (x_i + x_j)가 λ에 위치하는 i ≠ j와 함께_i x와 x가_j 존재할 것이다.그러나 이것은 두 개의 가장자리의 내부 지점을 연결하는 선 부분의 중간점이며, 따라서 다각형의 내부인 C에 놓여 있다.이것은 다시 C가 근본적인 영역이라는 사실과 모순된다.So remedctio ad lonelumm m ≤ 3 주장대로.

디리클레-보로노이 도메인

C = R의² 격자 Ⅱ에 대해서는 C의 정합적 구조를 이용하여 표준적으로 기본영역을 정의할 수 있다.C의 등호 변환 그룹은 복잡한 아핀 변환 g(z) = az + b에 의해 주어진다.이러한 변환은 최대 요인까지 유클리드 미터법 d(z, w) = z - w를 보존하며, 방향도 보존한다.뫼비우스 집단의 서브그룹으로 the에서 포인트를 고정하고 있다.미터법 구조는 λ의 모든 λ 0 0에 대해 C = {z: d(z, 0) < d(z, ))>로 표준적인 기본 도메인을 정의하는 데 사용할 수 있다.(기본 도메인이라는 정의로 보아 명백하다.)이것은 디리클레 도메인이나 보로노이 도표의 예인데, 복잡한 번역은 아벨리아 집단을 형성하므로 λ의 작용으로 통근하기 때문에 이러한 개념들이 일치한다.λ = Z + ZΩ, Im Ω > 0의 표준 기본 영역은 대칭 볼록 평행도 또는 중심 0의 육각형이다.순응적 등가성에 의해 기간 Ω을 추가로 제한하여 Re Ω Ω 1/2과 Ω 1을 만족시킬 수 있다. Diriclet이 보여준 것처럼("Dirichlet's 헥사곤 정리", 1850) 거의 모든 Ω에 대해 기본 영역은 육각이다.Re Ω > 0의 경우, 면의 중간점은 ±1/2, ± Ω/2, ±(Ω – 1)/2로 주어지며, 면은 정점을 완전히 결정하는 0에서 해당 반경을 2등분한다.실제로 첫 번째 꼭지점에는 x와 y real이 있는 (1 + ix)/2 및 Ω(1 + iy)/2 형식이 있어야 하므로, Ω = a + ib이면 – by = 1 및 x = b + ay.따라서 y = (a – 1)/b 및 x = (a²² + b – a)/b.따라서 6개의 꼭지점은 ±Ω(1 – iy)/2 및 ±(1 ± ix)/2이다.^[8]

상위 속에서의 기본 다각형

개요

모든 콤팩트한 리만 표면 X에는 간단히 연결된 리만 표면 X인 범용 커버 표면이 있다.X의 기본 집단은 X의 갑판 변형 역할을 하며 X의 생물학적 형태 집단의 부분군 γ으로 식별할 수 있다.따라서 그룹 γ은 X와 구별할 수 있는 콤팩트한 지수 공간 X//로 X에 자유롭게 작용한다.따라서 콤팩트한 리만 표면의 분류는 가능한 그룹 γ의 연구로 축소될 수 있다.균일화 정리 X에 의해 리만 구체, 복합 평면 또는 단위 디스크/상단 하프 평면이 된다.콤팩트한 리만 표면의 첫 번째 중요한 불변성분은 그 속(속)으로 아벨리아 그룹 //[,, ]]의 절반 등급이 부여한 위상학적 불변성이다(호몰로지 그룹 H₁(X, Z)로 식별할 수 있다).속은 피복 공간이 리만 구체일 경우 0, 복잡한 평면일 경우 1개, 단위 디스크 또는 상부 하프 평면일 경우 1개보다 크다.^[9]

리만 구의 생물 호몰로모르피즘은 단지 복잡한 뫼비우스 변환일 뿐이며, 해당하는 복잡한 행렬에는 항상 적어도 하나의 0이 아닌 고유 벡터가 있기 때문에 모든 비식별성 변환은 적어도 하나의 고정점이 있다.따라서 X가 리만 구체라면, X는 간단히 연결되고 리만 구체, 즉 0 리만 표면의 속인 리만 구에 생체형성되어야 한다.X가 복잡한 평면일 때, 생동형성의 그룹은 아핀 그룹, 즉 복합 뫼비우스 변환이 ∞을 고정하므로 변환 g(z) = az 0의 아즈 + b이다.고정점이 없는 비식별 변환은 a = 1과 b ≠ 0, 즉 0이 아닌 변환을 가진 변환일 뿐이다.따라서 그룹 γ은 속 1의 기본 다각형에 관한 절에서 설명한 바와 같이 C와 X의 격자 λ으로 식별할 수 있다.세 번째 경우, X가 단위 디스크 또는 상반부 평면일 때, 생체모형의 그룹은 단위 원이나 실제 축을 고정하는 복잡한 뫼비우스 변환으로 구성된다.전자의 경우, 변환은 그룹 SU(1, 1)/{±)의 요소에 해당한다.I}; 후자의 경우 실제 뫼비우스 변환에 해당하므로 SL(2, R)/{±나는.^[9]

콤팩트한 지수(첫 번째 종류의 푸치안 그룹)로 유닛 디스크나 상단 하프 평면에서 자유롭게 작용하는 가능한 그룹 γ의 연구와 분류는 아래에 설명된 바와 같이 기본적인 다각형을 연구함으로써 달성할 수 있다.푸앵카레가 관찰한 바와 같이 그러한 폴리곤은 각각 특별한 성질, 즉 볼록하고 옆구리 사이에 자연스러운 쌍을 이루고 있다.이러한 것들은 그룹을 회복할 수 있을 뿐만 아니라 발전기와 관계에 의한 그룹의 명시적인 표시를 제공한다.반대로 푸앵카레는 그러한 어떤 폴리곤도 콤팩트한 리만 표면을 만들어 낸다는 것을 증명했다; 사실, 푸앵카레의 폴리곤 정리는 보다 일반적인 폴리곤에 적용되었는데, 폴리곤은 이상적인 정점을 가질 수 있도록 허용되었지만 그의 증거는 그러한 정점 없이 컴팩트 케이스에서만 완성되었다.폴리곤의 볼록성에 대한 가정 없이, 시겔의 사상에 근거하여 마스킷과 드 람에 의해 완전한 증거가 제시되었으며, 비데돈(1983년), 이베르센(1992년), 스틸웰(1992년)에서 찾아볼 수 있다.카라테오도리는 슈바르츠 삼각형에 의한 테셀레이션의 존재, 즉 ,/a, inte/b, π/c 각도가 π 미만인 측지 삼각형에 의한 틸팅, 여기서 a, b, c는 정수인 경우 π보다 합이 작은 것을 기초적으로 취급했다.모든 각도가 π/2g일 때, 이것은 일반적인 4g 측 쌍곡 다각형에 의한 타일링을 설정하며, 따라서 계수형 g의 특정 콤팩트 리만 표면이 존재하는 것이다.생체모형 대칭의 주기적 그룹 Z를_2g 갖는 이 특별한 예는 아래 개발에서 사용된다.^[9]

콤팩트 리만 표면의 동형성 및 차이점성까지의 분류는 닫힌 방향성 2-매니폴드의 분류부터 동형성과 차이점성까지를 의미한다: 같은 속성을 가진 2-매니폴드 2개는 모두 차이점이다.사실 통합의 칸막이를 사용하는 모든 폐쇄적인 방향의 2마니폴드는 리만 계량법을 인정한다.콤팩트한 리만 표면의 경우, 등호성 메트릭도 도입될 수 있으므로, 홀오모르픽 좌표에서 ρ(z) dz 형식을 취한다. 일단 이 메트릭을 선택한 후에는, 국소적으로 생체동형 매핑은 정확하게 등호성인 차이점들을 보존한다. 즉, 매끄러운 함수에 의해 메트릭을 척도한다.등온 좌표의 존재는 - 라플라시안이나 벨트라미 방정식에 대한 국소적 존재 이론 중 하나를 사용하여 증명할 수 있다 - 모든 폐쇄 지향 리만 2-매니폴드에게 그 측정에 적합한 복잡한 구조를 부여할 수 있음을 보여주며, 따라서 콤팩트한 리만 표면의 구조를 가지고 있다.이 구조는 밀폐된 방향성 2-매니폴드의 분류가 차이점형 또는 동형성까지 콤팩트한 리만 표면의 경우로 축소될 수 있음을 보여준다.^[10]

콤팩트한 리만 표면의 동형성 및 차이점성까지의 분류는 기본 다각형을 사용하여 수행할 수 있다.실제로 푸앵카레가 관찰한 바와 같이 유클리드 공간에서 쌍곡선 공간으로 디리클레트의 방법을 적용하여 콤팩트 리만 표면 H/RW를 위한 볼록한 기본 폴리곤을 구성할 수 있다.그런 다음 네반린나와 조스트에 이어 γ의 단일 궤도에 정점이 놓여 있는 비콘벡스 폴리곤과 조각상 지오데틱 면을 산출하도록 기본 영역을 단계별로 수정할 수 있다.측면의 페어링 관계도 이러한 각 단계에서 수정된다.각 단계에는 폴리곤 내부의 대각선 지오데틱 세그먼트에 의해 폴리곤을 절단하고 페어링에 관여하는 뫼비우스 변환 중 하나를 사용하여 폴리곤을 재조립하는 작업이 포함된다.최종 쌍체 관계에서 어떤 두 개의 쌍체 측면도 원래 관계와 유사한 특성을 만족하는 공통 정점을 가질 수 없다.이 폴리곤은 내부의 대각선 조각 지오데틱 세그먼트로 절단한 후 폴리곤을 재조립하여 연속적으로 수정할 수 있다.최종 폴리곤은 4g 등가 정점을 가지며, 옆면은 조각처럼 지오데틱하다.옆면은 뫼비우스 변형을 쌍체 변형으로 하는 그룹 요소로 라벨을 표시한다.순서대로 라벨 표시는

${\displaystyle a_{1},b_{1},a_{1}^{-1},b_{1}^{1},\reason,a_{g},a_{g}^{-1},b_{g}^{1}, {-1},}$

γ은 단일 관계에 따라 a와_i b에_i 의해 생성된다.

${\displaystyle a_{1}b_{1}a_{1}a_{1}^{-1}^{-1}^{-1}\cdots a_{g}b_{g}a_{g}^{-1}b_{g}^{g}^{-1}=1.}$

• 

  0종표면(Sphere)

• 

  한 표면(토러스) 속

• 

  속2면

• 

  세 개의 표면속

교차로 번호 이론을 이용하여, 지오데틱스에 의해 정점을 결합하여 얻은 모양도 반드시 볼록한 것이 아닌 적절한 폴리곤이며, 또한 쌍을 이루는 같은 그룹 요소를 가진 기본 영역이기도 하다는 것을 따른다.이는 지오데틱 세그먼트에 의해 주어진 가장자리 및 표준 라벨 표시와 함께 기본적인 폴리곤을 산출한다.γ의 아벨리아화(Abelianization)는 2g 발전기를 가진 자유 아벨리아 그룹이다.따라서 g속은 위상학적 불변성이다.동일한 속성의 리만 표면 두 개가 위상학적 공간으로서 쌍체 간의 차이점형성으로 4g 면 폴리곤(클라인 모델에서 유클리드 폴리곤)의 측면을 식별하여 얻었기 때문에 위상학적 공간으로서 동형이라는 것을 쉽게 알 수 있다.^[11]이 구조를 일반 4g 면 폴리곤에 적용하면 리만 표면을 위상 입문서의 방향 표면 표준 설명인 g홀이 있는 도넛으로 토폴로지적으로 볼 수 있다.^[12][13]

몇 가지 추가 결과가 있다.

• 두 개의 동형 리만 표면은 서로 다르다.
• 속 g의 모든 볼록한 기본 폴리곤은 4g ≤ N – 12g – 6의 N 정점을 가진다.
• 속 g의 디리클레 폴리곤은 밀도가 높은 오픈 센트(centre) 세트를 위해 정확히 12g – 6정점을 가지고 있다.
• 모든 속 g Riemann 표면에는 Fricke 기본 폴리곤, 즉 양쪽 사이에 표준 쌍을 이루는 볼록 폴리곤이 있다.(폴리곤이 반드시 디리클레 폴리곤일 필요는 없다.)
• 기본 그룹의 생성자에 대한 적절한 정규화와 라벨링 후, Fricke polygon이 고유하게 결정되며, 이를 설명하는 6g – 6 실제 매개변수는 속 g의 Teichmüller 공간에 대한 전역 실제 분석 매개변수로 사용될 수 있다.

이러한 결과는 동형성과 기본군 사이의 상관관계와 연관되어 있다: 이는 리만 표면의 매핑 클래스 그룹, 즉 리만 표면 H/H 모듈의 퀘이콘 폼 자기 동형성의 그룹, 그리고 그 정체성에 대한 동형성의 집합이 Ⅱ(Dehn–)의 외부 자동화 그룹과 식별할 수 있다는 사실을 반영한다.닐슨-베어 정리).^[14]이러한 연결을 보려면 f가 X₁ = H/H의₁ quasiconformal homoporphism인 경우, X₂ = H/RW에₂ 대한 quasiconformal homoporphism f로 상승한다.이 리프트는 γ의₁ 요소들로 사전 구성되고 elements의₂ 요소들과 사후 구성까지 독특하다.만약 π이_i X에_i 대한 H의 투영이라면, f ∘ = π₁₂ f, γ은_i π_i g = π과_i 같은 H의 동형성 g의 그룹일 뿐이다. 만약 그 f g = θ (g) f를 따른다면, θ은 γ에₁₂ 대한 그룹 is의₁ 이형성인 것이다.f의 다른 선택은 내부 자동형성을 가진 구성으로 θ을 변화시킨다: 그러한 이소형성은 동등하다고 한다.^[15]

두 개의 이형성 θ과 θ형성은 해당 동형성 f와 f'가 동형성인 경우에만 동등하다.실제로 표면의 퀘이콘포형 자기 동형성 f가 신분 지도에 동질적일 경우에만 기본 집단의 내적 자동성을 유도한다는 것을 보여주기에 충분하다. 다시 말해, H/IV의 퀘이콘포형 자기 동형성 집단의 동형성은 그것이 주입되는 지도 등급 그룹으로 전달된다.실제로 F(t)가 F(0) = id, F(1) = f로 이루어진 자기 동형성의 연속 경로라고 먼저 가정해 보자.그 다음 F(0) = id를 가진 연속 리프트 F(t)가 있다.더욱이, in의 각 g에 대해, F(t) g g ( F(⁻¹t)는 t = 0에 대해 g와 동일한 continuously의 연속적인 변화 요소다. 따라서 γ의 미완성은 이 요소를 일정하게, 따라서 g와 같게 하여 F(t)가 γ과 교감하게 하므로 F(1)는 사소한 자동화를 유도한다.반면에 F가 γ의 내적 자동형성을 유도하는 f의 quasiconformal 리프트인 경우, 필요한 경우 γ 요소와의 조성을 거친 후 F가 γ과 통근한다고 가정할 수 있다.F는 quasiconformal이기 때문에 γ과도 통용되는 원의 quasymmetric homorphism까지 확장된다.γ의 각 g ≠ id는 쌍곡성이므로 원의 고정점 2개를 가지고 있어_± 다른 모든 점 z에 대해^±n g(z)가 무한대로 a를 경향이_± 있다.따라서 F는 이러한 점들을 고정해야 한다. 이러한 점들은 g가 변화함에 따라 원의 밀도가 높기 때문에 F는 단위 원을 고정한다.μ = F_z / F를_z 놓아 μ는 μ-invariant Beltrami 미분이다.단위 원에 3개의 점을 고정하기 위해 정규화된 Beltrami 방정식 tμ의 해결책이 F(t)가 되도록 한다.그런 다음 F(t)는 γ과 통근하므로 F = F(1)와 같이 단위 원 상의 ID가 된다.시공에 의한 F(t)는 ID와 F 사이의 동위원소다.이것은 주입력을 증명한다.^[15]

과부하 증명은 D의 쌍곡 메트릭과 γ의 단어 길이 메트릭을 비교하는 것에 의존한다.^[16]0이 볼록한 기본 폴리곤 C의 내부에 있고 g가 γ의 원소라고 가정할 때, 0에서 g(0)까지의 광선(쌍곡 지오데틱)은 C의 일련의 번역을 통과한다.이들 각각은 γ의 발전기 또는 발전기의 고정 생산물을 적용하여 이전 것들로부터 얻어진다(연속 번역기가 정점에서 만나는 경우).0과 g(0) 사이의 쌍곡 거리는 기본 다각형의 2배 직경의 g+의 4g보다 작다.따라서₁ length d(g, h) = L(hg⁻¹)이라는 단어로 정의된 L(hg)의 메트릭이 충족됨

${\displaystyle d(g(0),h(0)\leq a\,d_{1}(g,h)+b}$

양수 a와 b의 경우.반대로 다음과 같은 양의 상수 c와 d가 있다.

${\displaystyle d_{1}(g,h)\leq c\,d(g(0),h(0))+d.}$

디리클레 폴리곤

상단 하프 평면 H의 점 $z{\displaystyle {}_{}}$ ${\$과 상단 하프 평면에서 자유롭게 불연속적으로 작용하는 이산 부분군 γ(2, R)을 지정하면 Dirichlet 다각형을 점 집합으로 정의할 수 있다.

${\displaystyle F=\{z\in \mathbf {H} :d(z,z_{0})<d(z,gz_{0})\;\;\forall g\in \감마 ,g\neq 1\}}$

여기서 d는 상부 반면에 있는 쌍곡선 측정법이다.미터법 기본 폴리곤은 더 일반적으로 디리클레 폴리곤이라고 불린다.

• 이 근본적인 다각형은 근본적인 영역이다.
• 이 기본 폴리곤은 폴리곤의 어떤 두 점을 결합하는 지오데틱이 폴리곤 내부에 완전히 포함되어 있다는 점에서 볼록하다.
• F의 지름은 H/RW의 지름보다 작거나 같다.특히 F의 폐쇄는 콤팩트하다.
• 만약 γ에 H에 고정된 포인트가 없고 H/γ가 콤팩트하다면, F는 매우 많은 면을 가질 것이다.
• 폴리곤의 각 면은 지오데틱 호이다.
• 폴리곤의 모든 측면 s에 대해 precisely의 일부 g에 대해 gs = s s가 되도록 정확히 다른 면 s′가 있다.따라서, 이 다각형은 짝수의 면을 가질 것이다.
• 서로 횡방향으로 결합하는 그룹 요소 g의 집합은 generators의 생성기로, γ을 생성할 더 작은 집합은 없다.
• 상부 하프 평면은 γ의 작용에 따라 F의 폐쇄에 의해 타일링된다.즉, $H{\displaystyle }$= ${\displaystyle {\cup }_{}}$ g ∈ ${\displaystyle {\mathrm{g}}_{}}$ g ${\displaystyle g{}_{}}$ g $g$ {${\displaystyle \stackrel{}{}}${ { {$$\$displaystyle$ $H=\cup_{g\in \Gamma }\,g{\$$overline{F}}}}$가 F의 $폐점$인 것이다$.$

정규화 다각형

이 절에서는 임의의 디리클레 폴리곤에서 시작하여, 폴리곤을 4g 등가 정점과 측면의 표준 쌍을 갖는 비콘벡스 폴리곤으로 수정하기 위해 조스트(2002년)에 상세히 기술된 네반린나(1953)의 방법에 대한 설명이 제공된다.이 치료는 세이퍼트 & 트렐팔(1934년)에 제시된 방향성 2차원 다면체의 고전적 위상학적 분류에 대한 분석적 대응물이다.

프리케 표준 다각형

속 g의 리만 표면이 1개보다 큰 경우, 프리케는 또 다른 기본 폴리곤인 프리케 표준 폴리곤을 설명했는데, 이것은 디리클레트 폴리곤의 매우 특별한 예다.폴리곤은 표면의 기본 그룹의 표준 표시와 관련이 있다.프릭케의 원래 구조는 복잡하고, 프릭케 & 클라인(1897년)에 기술되어 있다.킨(1965)은 아흐포르스와 베르스의 퀘이콘 형식적 매핑 이론을 이용하여 프릭케의 건축에 대해 새롭고 짧고 더 정확한 버전을 제시하였다.Fricke 표준 폴리곤에는 다음과 같은 속성이 있다.

• Fricke polygon의 정점은 모두 γ의 궤도에 있는 4g 정점을 가지고 있다.꼭지점이란 양면이 만나는 지점을 의미한다.
• 면은 구별되는 쌍으로 매칭되어 있어, 쌍을 이루는 측으로 측면을 운반하는 γ의 독특한 요소가 있어 방향을 반대로 한다.γ의 동작은 방향보존이기 때문에 $한쪽$을 A ${\displaystyle A}$이라고 하면$,$ 다른 한쪽을 반대 방향 ${\displaystyle {\mathrm{A}}^{}}$- 1 ${\$로 표시할 수 있다$.$
• 표준 다각형의 가장자리는 인접한 면의 목록이 $A{\displaystyle {}_{}}$ 1 ${\displaystyle {B\mathrm{}}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {A\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}{}_{}^{}}$- 1 ${\displaystyle {\mathrm{B}}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$- ${\displaystyle 1_{}^{}}$ A ${\displaystyle {}_{}^{}{}_{}}$ ${\displaystyle {B\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {A\mathrm{}}_{}^{}}$ ${\displaystyle {2\mathrm{}}_{}^{}}$- 1 ${\displaystyle {}_{}^{}{}_{}^{}}$ ${\displaystyle 2_{}^{}{}_{}^{}}$- ${\displaystyle 1_{}^{}{}_{}{}_{}^{}}$ ${\displaystyle {}_{}}$ G ${\displaystyle G_{}^{}}$ -${\displaystyle 1_{}^{}}$ ${\displaystyle B_{}^{}}$ g${\displaystyle {}_{}^{}}$- ${\displaystyle 1_{}^{}}$ g A G - 1 ${\$1}B_${$$1$}의 형태를 취하도록 배열할 수 있다.$A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}$$A_{2}^{-1}B_{2}^{-1}^{-1}\cdots A_{g}B_{g}}$$A_{g}^{-1}B_{g}^{-1$즉, 한 쌍의 옆구리를 배열하여 이런 식으로 인터리브할 수 있다.
• 옆면은 지오데틱 호이다.
• 프릭케 폴리곤의 각 내부 각도는 π보다 엄격히 작기 때문에 폴리곤은 엄격히 볼록하며, 이러한 내부 각도의 합은 2π이다.

위의 구조는 폴리곤의 각 면이 리만 표면 H/RW에서 닫힌(비교) 루프임을 보증하기에 충분하다.As such, each side can thus an element of the fundamental group ${\displaystyle \pi _{1}(\mathbb {H} /\Gamma )\equiv \Gamma }$. In particular, the fundamental group ${\displaystyle \pi _{1}(\mathbb {H} /\Gamma )}$ has 2g generators ${\displaystyle A_1,B_1,A_2,B_2,\cdots A_g,{}_{}}$${\displaystyle B_{}}$ ${\displaystyle g_{}}$ ${\$},{g$}}}},$ 그리고 정확히 하나의 정의 제약조건이 있는 경우$,$

${\displaystyle A_{1}B_{$$1$$A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}$$A_{2}^{-1}B_{2}^{-1}^{-1}\cdots A_{g}B_{g}}$$A_{g}^{-1}B_{g}^{-1}=1$}$$$.$

Riemann 지표면 H/TH의 속은 g이다.

면적

표준 기본 폴리곤의 면적은 $4{\displaystyle \mathrm{}㎛(g}$- ${\displaystyle 1}$) ${\displaystyle 4\pi(g-1)}$이며, 여기서 g는 리만 표면의 속이다(동일하게, 여기서 4g은 폴리곤 면의 수).표준 폴리곤은 H/T를 대표하므로 리만 표면의 총 면적은 표준 폴리곤의 면적과 동일하다.면적 공식은 가우스-보넷 정리에서 따르며, 리만-을 통해 일반화된 어떤 의미에 있다.허위츠 공식.

표준 다각형에 대한 명시적 형식

회전 대칭이 있는 정규 표준 4g 측면 폴리곤에 대해 명시적 표현을 제공할 수 있다.이 경우 g-폴드 회전 대칭이 있는 속 $g{\displaystyle }$ ${\displaystyle g}$ Riemann$$ 표면의 경우, ${\displaystyle 2}$ g ${\displaystyle 2g}$ 생성기에$$ $의해{\displaystyle {}_{}}$ 그룹 a ${\displaystyle k_{}}$ ${\$를 부여할 수 있다$.$이러한 생성기는 상부 하프 평면에 작용하는 다음과 같은 부분 선형 변환에 의해 제공된다.

${\displaystyle a_{k}=\left({\begin{matrix}\cos k\alpha &-\sin k\alpha \\\sin k\alpha &\cos k\alpha \end{matrix}}\right)\left({\begin{matrix}e^{p}&0\\0&e^{-p}\end{matrix}}\right)\left({\begin{matrix}\cos k\alpha &\sin k\alpha \\-\sin k\alpha &\cos k\alpha \end{matrix}}\right)}$

< g $[\displaystyle 0\leq k<2g}$의 경우파라미터는 다음과 같이 제공된다.

${\displaystyle \cHB ={\frac {\pi }{4g}\왼쪽(2g-1\오른쪽)}$

그리고

${\displaystyle \cHB ={\frac {\pi }{4g}}}$

그리고

${\displaystyle p=\ln {\frac {\cos \cos \cos \cos \sqrt {\cos 2\cos \cos }{\sin \}}}}$

이러한 발전기가 제약 조건을 준수하는지 검증될 수 있다.

${\displaystyle a_{0}a_{1}1}\cdots a_{2g-1}a_{0}^{1}a_{1}^{1}1}^{1}\cdots a_{2g-1}^{-1}=1}$

그룹 프리젠테이션의 총체성을 보여주는 거야

참고 항목

• 케이리 그래프
• 유클리드 주
• 보로노이 다이어그램

메모들

참조

• Ahlfors, Lars V. (2006), Lectures on quasiconformal mappings, University Lecture Series, vol. 38 (Second ed.), American Mathematical Society, ISBN 978-0-8218-3644-6
• Appell, P.; Goursat, E.; Fatou, P. (1930), Théorie des fonctions algébriques d'une variable, Tome II, Fonctions automorphes, Gauthier-Vi]lars, pp. 102–154
• Bambah, R. P.; Davenport, H. (1952), "The covering of n-dimensional space by spheres", J. London Math. Soc., 27 (2): 224–229, doi:10.1112/jlms/s1-27.2.224
• Beardon, Alan F. (1983), The Geometry of Discrete Groups, Springer-Verlag, ISBN 978-0-387-90788-8
• Beardon, Alan F. (1984), A primer on Riemann surfaces, London Mathematical Society Lecture Note Series, vol. 78, Cambridge University Press, ISBN 978-0-521-27104-2
• Bonk, Marius; Schramm, Oded (2000), "Embeddings of Gromov hyperbolic spaces", Geom. Funct. Anal., 10 (2): 266–306, CiteSeerX 10.1.1.47.7874, doi:10.1007/s000390050009
• Böröczky, Károly, Jr. (2004), Finite packing and covering, Cambridge Tracts in Mathematics, vol. 154, Cambridge University Press, ISBN 978-0-521-80157-7
• Bourdon, Marc; Pajot, Hervé (2002), "Quasiconformal geometry and hyperbolic geometry", in Marc Burger; Alessandra Iozzi (eds.), Rigidity in dynamics and geometry, Springer, pp. 1–17, ISBN 978-3-540-43243-2
• Buser, Peter (1992), Geometry and spectra of compact Riemann surfaces, Progress in Mathematics, vol. 106, Birkhäuser, ISBN 978-0-8176-3406-3
• Cassels, J. W. S. (1997), "IX. Packings", An introduction to the geometry of numbers, Classics in Mathematics, Springer-Verlag, ISBN 978-3-540-61788-4
• Coxeter, H. S. M (1962), "The Classification of Zonohedra by Means of Projective Diagrams", J. Math. Pures Appl., 41: 137–156
• Coxeter, H. S. M.; Moser, W. O. J. (1980), Generators and relations for discrete groups, vol. 14 (Fourth edition. Ergebnisse der Mathematik und ihrer Grenzgebiete ed.), Springer-Verlag, ISBN 978-3-540-09212-4
• Eggleston, H. G. (1958), Convexity, Cambridge Tracts in Mathematics and Mathematical Physics, vol. Cambridge University Press
• Farb, Benson; Margalit, Dan (2012), A primer on mapping class groups, Princeton Mathematical Series, vol. 49, Princeton University Press, ISBN 978-0-691-14794-9
• Farkas, Hershel M.; Kra, Irwin (1980), Riemann Surfaces, Springer-Verlag, ISBN 978-0-387-90465-8
• Fenchel, Werner; Nielsen, Jakob (2003), Discontinuous groups of isometries in the hyperbolic plane, de Gruyter Studies in Mathematics, vol. 29, Walter de Gruyter, ISBN 978-3-11-017526-4
• Fricke, Robert; Klein, Felix (1897), Vorlesungen über die Theorie der automorphen Funktionen, Band 1: Die gruppentheoretischen Grundlagen, Teubner, pp. 236–237, 295–320
• Grünbaum, Branko; Shephard, G. C. (1987), Tilings and patterns, W. H. Freeman, ISBN 978-0-7167-1193-3
• Guggenheimer, H. (1977), "The Jordan curve theorem and an unpublished manuscript by Max Dehn" (PDF), Archive for History of Exact Sciences, 17 (2): 193–200, CiteSeerX 10.1.1.374.1893, doi:10.1007/BF02464980, JSTOR 41133486, MR 0532231
• Hirsch, Morris W. (1994), Differential topology, Graduate Texts in Mathematics, vol. 33, Springer-Verlag, ISBN 978-0-387-90148-0
• Imayoshi, Y.; Taniguchi, M. (1992), An Introduction to Teichmüller spaces, Springer-Verlag, ISBN 978-0-387-70088-5
• Iversen, Birger (1992), Hyperbolic geometry, London Mathematical Society Student Texts, vol. 25, Cambridge University Press, ISBN 978-0-521-43508-6
• Jost, Jurgen (2002), Compact Riemann Surfaces (2nd ed.), Springer-Verlag, ISBN 978-3-540-43299-9
• Kapovich, Ilya; Benakli, Nadia (2002), "Boundaries of hyperbolic groups", Combinatorial and geometric group theory, Contemp. Math., vol. 296, American Mathematical Society, pp. 39–93
• Keen, Linda (1965), "Canonical polygons for finitely generated Fuchsian groups", Acta Math., 115: 1–16, doi:10.1007/bf02392200
• Keen, Linda (1966), "Intrinsic moduli on Riemann surfaces", Ann. of Math., 84 (3): 404–420, doi:10.2307/1970454, JSTOR 1970454
• Kolmogorov, A. N.; Yukshkevich, A. P., eds. (2001), Mathematics of the 19th Century: Mathematical Logic, Algebra, Number Theory, Probability Theory, Springer, ISBN 978-3764364410
• Lehto, Olli (1987), Univalent functions and Teichmüller spaces, Graduate Texts in Mathematics, vol. 109, Springer-Verlag, ISBN 978-0-387-96310-5
• Lyusternik, L. A. (1966), Convex figures and polyhedra, translated by Donald L. Barnett, Boston: D. C. Heath and Co.
• Nevanlinna, Rolf (1953), Uniformisierung, Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete (in German), vol. 64, Springer-Verlag
• Seifert, Herbert; Threlfall, William (1934), A textbook of topology, Pure and Applied Mathematics, vol. 89, translated by Michael A. Goldman, Academic Press, ISBN 978-0-12-634850-7
• Shastri, Anant R. (2011), Elements of differential topology, CRC Press, ISBN 978-1-4398-3160-1
• Siegel, C. L. (1971), Topics in complex function theory, Vol. II. Automorphic functions and abelian integrals, translated by A. Shenitzer; M. Tretkoff, Wiley-Interscience
• Stillwell, John (1992), Geometry of surfaces, Universitext, Springer-Verlag, ISBN 978-0-387-97743-0
• Zong, Chuanming (2014), "Packing, covering and tiling in two-dimensional spaces", Expositiones Mathematicae, 32 (4): 297–364, doi:10.1016/j.exmath.2013.12.002