함수의 그래프

이 기사는 검증을 위해 추가 인용이 필요합니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 기사를 개선하는 데 도움을 주세요. 출처가 없는 재료는 문제가 발생하여 제거될 수 있습니다. 출처 찾기 : "Graph of a function" – 뉴스 · 신문 · 서적 · 학자 · JSTOR (2014년 8월) (본 템플릿 메시지 제거 방법 및 시기에 대해 알아보기)

기능.
x ↦ f (x)
함수 개념의 연혁
도메인 및 코도메인 예제
${\displaystyle X}$ → ${\displaystyle \mathbb{B}}$ ${\$ ${\displaystyle \mathbb {B}}$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathbb {B} ^{n}}$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb{Z}}$ ${\$ ${\displaystyle \mathbb {Z}}$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb{R}}$ ${\$ ${\displaystyle \mathbb {R}}$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathbb {R} ^{n}}$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb{C}}$ ${\$ ${\displaystyle \mathbb {C}}$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathbb {C} ^{n}}$ → ${\displaystyle X}$
클래스/속성
일정한 신원 선형 다항식 합리적인 대수학 분석적 매끄러운 계속되는 측정가능 인젝티브 서젝티브 바이젝티브
시공
제한 구성. λ 인버스
일반화
부분적 멀티밸류 암시적 공간
v t

수학에서 함수 $f$ ${\displaystyle$ f$}$의 그래프는 순서쌍$({\displaystyle x,}$ y${\displaystyle )}$ ${\displaystyle (x,$ y$)}$의 집합이며$,$ $여기$서 f${\displaystyle }$(${\displaystyle x}$) = ${\displaystyle y}$.$${\displaystyle f(x) = y.}$$ $x{\displaystyle }$ ${\displaystyle x}$와 $f{\displaystyle }$(${\displaystyle x)}$ ${\displaystyle f(x)}$가 실수인 일반적인 경우, 이 쌍들은 평면에 있는 점들의 직각좌표이며 종종 곡선을 형성합니다.함수의 그래프를 그래프로 표현하는 것을 그림이라고도 합니다.

두 변수의 함수, 즉 도메인이 쌍$({\displaystyle x,}$ y${\displaystyle )}$ ${\displaystyle (x,$ y$)}$ – 로 구성된 함수의 경우 그래프는 일반적으로 순서가 지정된 삼중$({\displaystyle x,}$ y${\displaystyle ,}$ ${\displaystyle z)}$ ${\displaystyle (x, y,$ z$)}$ 집합을 나타냅니다. 여기서 $f{\displaystyle }$(${\displaystyle x,}$ ${\displaystyle y)}$ = ${\$displaystyle f (x, y) = z}.이것은 3차원 공간의 부분 집합입니다. 두 개의 실제 변수의 연속적인 실수 값 함수의 경우 그래프가 표면을 형성하고 표면 그림으로 시각화할 수 있습니다.

과학, 공학, 기술, 금융 및 기타 영역에서 그래프는 여러 용도로 사용되는 도구입니다.가장 단순한 경우에는 일반적으로 직사각형 축을 사용하여 한 변수가 다른 변수의 함수로 표시됩니다. 자세한 내용은 그림(그래픽)을 참조하십시오.

함수의 그래프는 관계의 특수한 경우입니다.현대 수학의 기초, 그리고 일반적으로 집합론에서 함수는 실제로 그 그래프와 같습니다.^[1]그러나 함수는 입력과 ^[2]출력의 관계뿐만 아니라 어떤 집합이 도메인이고 어떤 집합이 코도메인인지로 구성되는 매핑으로 보는 것이 유용할 때가 많습니다.예를 들어, 함수가 코도메인 위에 있는지 여부를 고려해야 합니다.함수 자체의 그래프가 코드 도메인을 결정하는 것은 아닙니다.동일한 대상으로 간주되더라도 다른 관점에서 보는 것을 나타내기 때문에 함수와 함수의 그래프라는 용어를 모두 사용하는 것이^[3] 일반적입니다.

정의.

집합 X(도메인)에서 집합 Y(코드 도메인)까지의 함수 $f{\displaystyle :}$ ${\displaystyle X}$ → ${\displaystyle Y}$ {\$displaystyle$ $f:X\to$ Y$}$가 주어지면, 함수의 그래프는 집합입니다.

이것은 데카르트 곱 ${\displaystyle }$×${\displaystyle Y}$ {\$displaystyle X\times$ Y$}$의 부분집합입니다$.$ 집합론에서 함수의 형식적 정의에서 함수의 그래프는 실제로 함수 자체와 같습니다.

예

한 변수의 함수

함수 $f{\displaystyle :}$ {1${\displaystyle ,}$ ${\displaystyle 2,}$ ${\displaystyle 3}$ ${\displaystyle \}}$→${\displaystyle }${${\displaystyle a}$, ${\displaystyle b,}$ ${\displaystyle c,}$ ${\displaystyle d\}}$ ${\displaystyle f:\{1, 2,$ 3$\}\$to $\{a,$ b,$c, d\}}$의 그래프는 다음과 같이 정의됩니다.

집합${\displaystyle }${1${\displaystyle ,}$ ${\displaystyle 2,}$ 3 ${\displaystyle \}}$×${\displaystyle }${${\displaystyle a,}$ b${\displaystyle ,}$ ${\displaystyle c,}$ d${\displaystyle \}}$ ${\displaystyle \{1, 2,$ 3$\}\times \{a,$ b,$c,$ d$\}$의 부분 집합입니다.

그래프에서 도메인$${${\displaystyle 1,}$ ${\displaystyle 2,}$ ${\displaystyle 3\}}$ ${\displaystyle \{1,$ ${\displaystyle 2}$$,$ ${\displaystyle 3}$$\}$ {\displaystyle \{${\displaystyle 1,}$ 2${\displaystyle ,}$ $3$${\displaystyle \}}$ =${\displaystyle }${ $x$: ∃ y}, 즉 (x, y) ∈ G (f ) } {\displaystyle \{1, 2, 3\} =\{x:\ exists y,{\text{ 이러한 }(x, y)\in G(f)\}}로 복구할 수 있습니다. 마찬가지로 범위도 {a,}로 복구할 수 있습니다.${\displaystyle c,}$ ${\displaystyle d}$ ${\displaystyle \}}$=${\displaystyle }${$$y : ($x$$,$ y )${\displaystyle }$∈ G (f ) } {\displaystyle \{a,c,d\}${\displaystyle }$=\{y:\displayx,{\text{ that }}(x,y)\in G(f)\}. 그러나 코드 도메인 {a, b, c, d} {\displaystyle \{a,b,c,d\}는 그래프만으로는 확인할 수 없습니다.

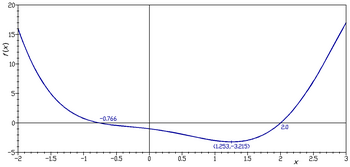
실수선 위의 3차 다항식의 그래프

아.

이 집합을 직각면에 표시하면 결과는 곡선이 됩니다(그림 참조).

두 변수의 함수

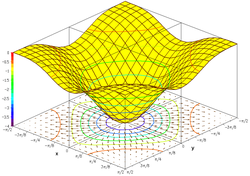
삼각함수의 그래프

아.

이 집합을 3차원 직각좌표계에 표시하면 결과는 표면이 됩니다(그림 참조).

그래프, 함수의 기울기 및 여러 수준 곡선으로 표시하는 것이 도움이 되는 경우가 많습니다.레벨 곡선은 함수 표면에 매핑되거나 하단 평면에 투영될 수 있습니다.두 번째 그림은 함수의 그래프를 보여줍니다.

참고 항목

참고문헌

더보기

외부 링크

• 바이스타인, 에릭 W "함수 그래프"From MathWorld—Wolfram 웹 리소스.