수학 에서, 주어진 지점 x 에서 주어진 벡터 v 를 따라 다변량 변이성(scalar) 함수 의 방향성 파생물은 직관적으로 함수의 순간 변화율을 나타내며, v 가 지정한 속도로 x 를 통과한다.
한 지점(예: 위치) x 의 벡터 v에 대한 스칼라 함수 의 방향성 파생물은 다음 중 하나로 나타낼 수 있다.
∇ v f ( x ) = f v ′ ( x ) = D v f ( x ) = D f ( x ) ( v ) = ∂ v f ( x ) = v ⋅ ∇ f ( x ) = v ⋅ ∂ f ( x ) ∂ x {\displaystyle \nabla _{\mathbf {v} }{f}(\mathbf {x} )=f'_{\mathbf {v} }(\mathbf {x} )=D_{\mathbf {v} }f(\mathbf {x} )=Df(\mathbf {x} )(\mathbf {v} )=\partial _{\mathbf {v} }f(\m atsbf {x}=\mathbf {v} \cdot {\cdla mathbf {x})}=\mathbf {v} \cdot {\frac {\f mathbf {x} mathbf {x 따라서 그것은 곡선 좌표 곡선 중 하나를 따라 변화율이 취해지고 다른 모든 좌표는 일정하게 되는 부분파생상품 의 개념을 일반화한다. 방향파생상품은 가토파생상품 의 특수한 경우다.
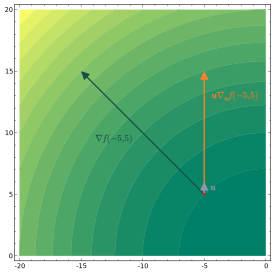
정의 검정색으로 그라데이션 벡터를 표시하는 f( x y 2 2 {\ displaystyle f(x,y)=x^{2}+y^{2}} 등고선도와 주황색으로 표시된u {\ displaystyle \mathbf {u} u {\ displaysty 그라데이션 벡터는 함수의 최대 증가율 방향의 그라데이션 점 때문에 더 길다. 스칼라 함수 의 방향 유도체
f ( x ) = f ( x 1 , x 2 , … , x n ) {\displaystyle f(\mathbf {x} )=f(x_{1},x_{2},\ldots,x_{n}}}} 벡터를 따라.
v = ( v 1 , … , v n ) {\displaystyle \mathbf {v} =(v_{1},\ldots ,v_{n})} 함수 v {\ displaystyle \nabla _{\mathbf {v}{f ( 한계 에[1]
∇ v f ( x ) = 임이 있는 h → 0 f ( x + h v ) − f ( x ) h . {\displaystyle \mathbf {v}{{\mathbf {x}}=\lim_{h\to 0}{\frac {f(\mathbf {x} +h\mathbf {v})-f(\mathbf {x}}}{h}}}}}}. } 이 정의는 예를 들어 벡터(따라서 단위 벡터)의 규범이 정의되지 않은 광범위한 맥락에서 유효하다.[2]
서로 다른 기능의 경우 함수 f 가 x 에서 서로 다른 경우 방향파생물은 벡터 v 를 따라 존재하며, 하나는
∇ v f ( x ) = ∇ f ( x ) ⋅ v {\displaystyle \mathbf {v}{f}{f}(\mathbf {x} )=\mathbf(\mathbf {x} )\cdot \mathbf {v}}}} 오른쪽의 on {\displaystyle la } ) gradient displaystyle \cdot } 도트 제품 이다.[3] 이는 경로 h( t x v {\displaystyle h(t)=x+tv}
0 = 임이 있는 t → 0 f ( x + t v ) − f ( x ) − t D f ( x ) ( v ) t = 임이 있는 t → 0 f ( x + t v ) − f ( x ) t − D f ( x ) ( v ) = ∇ v f ( x ) − D f ( x ) ( v ) → ∇ f ( x ) ⋅ v = D f ( x ) ( v ) = ∇ v f ( x ) {\displaystyle {\begin{aligned}0&=\lim _{t\to 0}{\frac {f(x+tv)-f(x)-tDf(x)(v)}{t}}\\&=\lim _{t\to 0}{\frac {f(x+tv)-f(x)}{t}}-Df(x)(v)=\nabla _{v}f(x)-Df(x)(v)\\\rightarrow &\nabla f(\mathbf {x} )\cdot \mathbf {v} =Df(x)(v)=\nabla _{\mathbf {v} }{f}(\mathbf {x} )\end{aligned}}} 직감적으로 f 지점 x 에서 f 의 방향적 파생상품은 x 지점 을 지나 이동할 때 시간에 대한 v 방향 으로 f 의 변화율 을 나타낸다.
벡터 방향만 사용 절단면이 경사 A 의 방향을 포함하는 경우 접선 A 와 수평 사이의 각도 α 는 최대가 될 것이다. 유클리드 공간 에서, 일부[4] 정규화 후 임의의 0이 아닌 벡터 v와 관련되도록 정의하고, 따라서 그 규모와 독립적이며 그것의 방향에만 의존한다.[5]
이 정의는 v 가 지정한 방향으로 이동하는 거리 단위당 f 의 증가 속도를 제공한다. 이 경우, 한 사람이 가지고 있다.
∇ v f ( x ) = 임이 있는 h → 0 f ( x + h v ) − f ( x ) h v , {\displaystyle \mathbf {v}{{\mathbf {x}=\mathbf {x}{h\frac {f}+h\mathbf {v}}}{h \mathbf {v}}}{h \mathbf {v}}}}}}},},},} 또는 만약 f가 x 에서 다를 수 있다면,
∇ v f ( x ) = ∇ f ( x ) ⋅ v v . {\displaystyle \mathbf {v}{{\mathbf {x}}=\mathbf {x}=\mathbf(\mathbf {x})\cdot {\frac {\mathbf {v}{\mathbf {v}}}}}}} 단위 벡터에 대한 제한 유클리드 공간 의 함수의 맥락에서, 일부 텍스트는 벡터 v 를 단위 벡터 로 제한한다. 이 제한으로 위의 두 정의는 동일하다.[6]
특성. 일반 파생상품 의 많은 익숙한 특성들은 방향 파생상품에 대한 것이다. 여기에는 p:의 인접 지역에서 정의되는 f 및 g 기능 에 대해 다음 과 같이 구별할 수 있는 p:
합계 규칙 ∇ v ( f + g ) = ∇ v f + ∇ v g . {\displaystyle \mathbf {v}}(f+g)=\mathbf {v}}{\mathbf {v}\f+\mathla _{\mathbf {v}g.} 상수 요인 규칙 모든 상수 c에 대해, ∇ v ( c f ) = c ∇ v f . {\displaystyle \nabla _{\mathbf {v}}}}(cf)=c\mathla _{\mathbf {v}f. } 제품 규칙 라이프니츠의 규칙 ): ∇ v ( f g ) = g ∇ v f + f ∇ v g . {\displaystyle \mathbf {v}}}(fg)=g\mathbf {v}{\mathbf {v}{f+f\messla _{\mathbf {v}g.} chain g 가 p 에서 다르고 h가 g (p )에서 다르면 ∇ v ( h ∘ g ) ( p ) = h ′ ( g ( p ) ) ∇ v g ( p ) . {\displaystyle \mathbf {v}(h\mathbf {p})(\mathbf {p})=h'=h'(g(\mathbf {p})\mathbf {v}g(\mathbf {p}). } 차동 기하학에서 M 차별성 있는 다지관 이 되게 하고, p f p p 구별 할 수 있다고 가정해 보자. If v tangent vector to M p directional derivative of f v df (v )Exterior derivative ), ∇ v f ( p ) {\displaystyle \nabla _{\mathbf {v} }f(\mathbf {p} )} Covariant derivative ), L v f ( p ) {\displaystyle L_{\mathbf {v} }f(\mathbf {p} )} Lie derivative ), or v p f {\displaystyle {\mathbf {v} }_{\mathbf {p} }(f)}( 도원을 통한 접선 공간 § 정의 참조)는 다음과 같이 정의할 수 있다. γ [-1, 1] → M γ (0) p γ ′(0)v
∇ v f ( p ) = d d τ f ∘ γ ( τ ) τ = 0 . {\displaystyle \ \la _{\mathbf {v} }f(\mathbf {p} )=\왼쪽. {\frac {d}{d\tau }{d\}f\f\f\not \cHB(\tau )\right _{\tau =0}} 이 정의는 γ ′(0) v 선택 γ
더 리 파생상품 벡터장 V μ (x W μ ( ) {\displaystyle W^{\mu }(x)} Lie 파생상품 은 두 방향 유도체(반사가 사라지는 경우)의 차이에 의해 제공된다
L V W μ = ( V ⋅ ∇ ) W μ − ( W ⋅ ∇ ) V μ . {\displaystyle {\mathcal{L}_{V} W^{\mu }=(V\cdot \nabla ) W^{\mu }-(W\cdot \nabla )V^{\mu }} 특히 스칼라 필드 ϕ x {\displaystyle \phi (x)} ,
L V ϕ = ( V ⋅ ∇ ) ϕ . {\displaystyle {\mathcal{L}_{V}\phi =(V\cdot \nabla )\phi .} 리만 텐서 방향 유도체는 흔히 리만 곡률 텐서 의 도입 파생에 사용된다. 한쪽 가장자리를 따라 최소 벡터 Δ , 다른 가장자리를 따라 Δ³ 의 곡선 사각형을 고려한다. 우리는 탐욕자 S 를 Δ 를 따라 번역한 다음 Δ ′을 따라 번역한 다음 Δ ′을 따라 번역을 빼낸다. 부분파생상품을 이용하여 방향파생상품을 만드는 대신에 공변량파생상품 을 사용한다. Δ 에 대한 번역 연산자는 다음과 같다.
1 + ∑ ν δ ν D ν = 1 + δ ⋅ D , {\displaystyle 1+\sum _{\nu }\delta ^{\nu }D_{\nu }=1+\delta \cdot D,} 그리고 Δ³ 의 경우,
1 + ∑ μ δ ′ μ D μ = 1 + δ ′ ⋅ D . 1+\sum _{\mu }\delta '^{\mu }D_{\mu }=1+\delta '\cdot D. } 그 두 길의 차이는 바로 그때다.
( 1 + δ ′ ⋅ D ) ( 1 + δ ⋅ D ) S ρ − ( 1 + δ ⋅ D ) ( 1 + δ ′ ⋅ D ) S ρ = ∑ μ , ν δ ′ μ δ ν [ D μ , D ν ] S ρ . {\displaystyle(1+\delta '\cdot D)(1+\delta \cdot D) S^{\rho }-(1+\delta \cdot D)(1+\delta '\cdot D)(1+\delta '\cdot D) S^{\rho }=\sum _{\mu ,\nu }\delta '^{\mu }\delta ^{\nu }}[D_{\mu }}}}}{\rho }}}}} 공변량 파생상품의 비확정성은 다지관의 곡률을 측정한다고 주장할[7]
[ D μ , D ν ] S ρ = ± ∑ σ R σ ρ μ ν S σ , {\displaystyle [D_{\mu }},D_{\nu }]S_{\rho }=\pm \sigma }{\rho \mu \nu }{}S_{\sigma }}}}}}}}} 여기서 R 은 리만 곡률 텐서이고 기호는 저자 의 사인 규약에 따라 달라진다.
집단 이론에서 번역 푸앵카레 대수학 에서는 극소수 번역 연산자 P 를 다음과 같이 정의할 수 있다.
P = i ∇ . {\displaystyle \mathbf {P} =i\nabla .} (i 는 P 가 자기 적응 연산자임 을 보장한다) 유한 변위 λ 에 대해, 번역을 위한 단일 힐버트 공간 표현 은 다음과[8]
U ( λ ) = 생략하다 ( − i λ ⋅ P ) . {\displaystyle U({\boldsymbol {\lambda }})=\exp \left(-i{\boldsymbol {\lambda }}}\cdot \mathbf {P} \right) } 위의 최소 번역 연산자의 정의를 이용하여 유한 번역 연산자는 다음과 같이 강조된 방향 파생상품임을 알 수 있다.
U ( λ ) = 생략하다 ( λ ⋅ ∇ ) . {\displaystyle U({\boldsymbol {\lambda }}})=\exp \left({\boldsymbol {\lambda }}}\cdot \nabla \right). } 다변량함수 f (x )에 대해 작용한다는 의미에서 번역 연산자다.
U ( λ ) f ( x ) = 생략하다 ( λ ⋅ ∇ ) f ( x ) = f ( x + λ ) . {\displaystyle U({\boldsymbol {\lambda }}f(\mathbf {x})=\ex \mathbol {\lambda {x}}\cdot \nabla \right)=f(\mathbf {x}+{\bmbmbmobda}}}}}}}}}}}}}}}}}}. } 마지막 방정식의 증명 표준 단변량 미적분학에서, 평활함수 f (x )의 파생상품은 (소형 ε )에 의해 정의된다.
d f d x = f ( x + ε ) − f ( x ) ε . {\dplaystyle {\frac {df}{dx}={\frac {f(x+\varepsilon )-f(x)}{\barepsilon }}. } f (x +ε )를 찾도록 다시 정렬할 수 있음:
f ( x + ε ) = f ( x ) + ε d f d x = ( 1 + ε d d x ) f ( x ) . {\displaystyle f(x+\varepsilon )=f(x)+\varepsilon \,{\frac {df}{dx}}}}=\좌측(1+\barepsilon \,{\frac {d}{dx}\right)f(x)f. } [ 1 ε d d ] {\displaystyle [1+\varepsilon \,(d/dx)]} 이는 즉시 다변량 함수 f (x )로 일반화된다[9]
f ( x + ε ) = ( 1 + ε ⋅ ∇ ) f ( x ) . {\displaystyle f(\mathbf {x} +{\mathsymbol {\barepsilon }}})=\좌측(1+{\numbsymbol {\\barepsilon }}}}\cdot \cdatabf \x}}}} 여기서 ε ⋅ \{\displaystyle boldsymbol barepsilon cdot nabla }} ε 우리는 번역 연산자의 최소 버전을 찾았다.
U ( ε ) = 1 + ε ⋅ ∇ . {\displaystyle U({\boldsymbol {\barepsilon }})=1+{\boldsymbol {\barepsilon }}\cdot \nabla .} 그룹 곱셈법[10] U (g )U (f )=U (gf )가 그 형태를 취하고 있는 것은 분명하다.
U ( a ) U ( b ) = U ( a + b ) . {\displaystyle U(\mathbf {a} )U(\mathbf {b})=U(\mathbf {a+b}). } 그러므로 유한 변위 λ 부분 으로 나눈다고 가정하자(N →∞은 어디에나 함축되어 있다) λ N =ε 바꾸어 말하면, 환언하면
λ = N ε . {\displaystyle {\boldsymbol {\lambda }}=N{\boldsymbol {\barepsilon }}. } 그 다음 U(수치 N times를 적용 하여 U(수치
[ U ( ε ) ] N = U ( N ε ) = U ( λ ) . {\displaystyle [U({\boldsymbol {\barepsilon }}})]^ {N}=U(N{\boldsymbol {\barepsilon }}})= U({\boldsymbol {\lambda }}). } 이제 U(U )에 대해 위의 표현을 연결할 수 있다.
[ U ( ε ) ] N = [ 1 + ε ⋅ ∇ ] N = [ 1 + λ ⋅ ∇ N ] N . {\displaystyle [U({\boldsymbol {\barepsilon }}})]^ {N}=\left[1+{\boldsymbol {\varepsilon }}}\cdot \nabla \right]^ {N}=\왼쪽[1+{\frac {{\boldsymbol {\lambda }}}\cdot \nabla }{N}\오른쪽]^ {N}} ID[11]
생략하다 ( x ) = [ 1 + x N ] N , {\displaystyle \exp(x)=\왼쪽[1+{\frac {x}{N}\오른쪽]^ {N}} 우리는 가지고 있다.
U ( λ ) = 생략하다 ( λ ⋅ ∇ ) . {\displaystyle U({\boldsymbol {\lambda }}})=\exp \left({\boldsymbol {\lambda }}}\cdot \nabla \right). } 그리고 U(()f (x )=f (x +) 이후
[ U ( ε ) ] N f ( x ) = f ( x + N ε ) = f ( x + λ ) = U ( λ ) f ( x ) = 생략하다 ( λ ⋅ ∇ ) f ( x ) , {\displaystyle [U({\boldsymbol {\varepsilon }})^{{\mathbf {x} +N{\boldsymbol {\varepsilon }}}=f(\mathbf {x} +{\boldsymbollambda }}}}}}}}}}}}}}}}}}}}===)===}= U({\boldsymbol {\lambda }})f(\mathbf {x} )=\exp \exp({\boldsymbol {\lambda }}}\cdot \nabla \right)f(\mathbf {x}),}),} Q.E.D.
기술적 참고사항으로서 이 절차는 번역군이 푸앵카레 대수학에서 아벨 의 하위그룹 (카탄 하위그룹 )을 형성하기 때문에 비로소 가능하다. 특히 집단 곱셈법 U (a )U (b ) = U (a +b )를 당연시해서는 안 된다. 우리는 또한 Poincaré가 연결된 Lie 그룹이라는 것을 주목한다. 리얼 파라미터의 연속적인 집합에 의해 설명되는 변환 T(ξ )의 그룹이다. ξ {\ displaystyle \xi a 집단 곱셈법은 형태를 취한다.
T ( ξ ¯ ) T ( ξ ) = T ( f ( ξ ¯ , ξ ) ) . {\displaystyle T({\bar {\xi }) T(\xi )=T({\bar {\xi }},\xi )). } ξ a {\displaystyle \xi ^{a}=0}
f a ( ξ , 0 ) = f a ( 0 , ξ ) = ξ a . {\displaystyle f^{a}(\xi ,0)=f^{a}(0,\xi )=\xi ^{a}. } 힐버트 공간의 실제 운영자는 단일 운영자 U (T )에 의해 대표된다. 위의 표기법에서 우리는 T 를 억압하였고, 이제 U (λ )를 U (P (λ )로 표기하였다. 아이덴티티 주변에 있는 작은 이웃의 경우, 파워 시리즈는
U ( T ( ξ ) ) = 1 + i ∑ a ξ a t a + 1 2 ∑ b , c ξ b ξ c t b c + ⋯ {\displaystyle U(\xi )=1+i\sum _{a}\i ^{a}_{a}+{a}+{a}+{a}+{b,c}\sum _{b,c}\xi ^{c}t_{bc}+\codots}}}}}}}}}}} 꽤 괜찮다. U(T)가 비프로젝트적 표현(즉, 비프로젝트적 표현)을 형성한다고 가정한다.
U ( T ( ξ ¯ ) ) U ( T ( ξ ) ) = U ( T ( f ( ξ ¯ , ξ ) ) ) . {\displaystyle U({\bar {\xi }) U(T(\xi )=U({\bar {\xi },\xi )). } f에서 2차 전력으로의 확장은
f a ( ξ ¯ , ξ ) = ξ a + ξ ¯ a + ∑ b , c f a b c ξ ¯ b ξ c . {\displaystyle f^{a}({\bar {\xi }},\xi )=\xi ^{a}+{\ba}++\sum_{b,c}f^{bar {\xi }{bar}}{ba}}\xi ^{c}. } 표현 곱셈 방정식을 확장하고 계수를 등분시킨 후, 우리는 비교조건이 있다.
t b c = − t b t c − i ∑ a f a b c t a . {\displaystyle t_{bc}=--t_{b}t_{c}-i\sum _{a}f^{f^}t_{a}. } t b {\ displaystyle t_{ab}} 표준 Lie 대수 정류자를 가지고 있다.
[ t b , t c ] = i ∑ a ( − f a b c + f a c b ) t a = i ∑ a C a b c t a , {\displaystyle [t_{b},t_{c}]=i\sum _{a}(-f^{abc}+f^{acb}t_{a}=i\sum _{a}C^{abc}t_{a}}}}},} C 와 함께 구조물이 일정 하게 유지된다. 번역용 발전기는 부분파생상품 사업자로 통근한다.
[ ∂ ∂ x b , ∂ ∂ x c ] = 0. {\displaystyle \left[{\frac {\properties }{b}},{\frac }{\frac }{\preason x^{c}}}\right]=0. } 이는 구조물 상수가 사라지고 따라서 f 팽창의 2차 계수도 사라진다는 것을 의미한다. 즉, f 는 단순히 첨가물일 뿐이다.
f 아벨의 a ( ξ ¯ , ξ ) = ξ a + ξ ¯ a , {\displaystyle f_{\text{abelian}^{a}({\bar {\xi },\xi )=\xi ^{a}+{\bar{\xi }}} 그래서 아벨 그룹에게는
U ( T ( ξ ¯ ) ) U ( T ( ξ ) ) = U ( T ( ξ ¯ + ξ ) ) . {\displaystyle U({\bar {\xi }) U(T(\xi )=U({\bar {\xi }}+\xi )). } Q.E.D.
회전 또한 회전사업자 는 방향파생상품을 포함한다. 각도θ ^ θ θ θ displaystyle {\hat {\theta }}}={\boldsymbol theta }/\ta }}.
U ( R ( θ ) ) = 생략하다 ( − i θ ⋅ L ) . {\displaystyle U(R(\mathbf {\theta } )=\exp(-i\mathbf {\theta } \cdot \mathbf {L}). } 여기서 L 은 SO (3) 를 생성하는 벡터 연산자다.
L = ( 0 0 0 0 0 1 0 − 1 0 ) i + ( 0 0 − 1 0 0 0 1 0 0 ) j + ( 0 1 0 − 1 0 0 0 0 0 ) k . {\displaystyle \mathbf {L} ={\begin{pmatrix}0&0&0\\0&0&1\\0&-1&0\end{pmatrix}}\mathbf {i} +{\begin{pmatrix}0&0&-1\\0&0&0\\1&0&0\end{pmatrix}}\mathbf {j} +{\begin{pmatrix}0&1&0\\-1&0&0\\0&0&0\end{pmatrix}}\mathbf {k} .} 최소의 오른손 회전은 위치 벡터 x 를 다음과 같이 변화시키는 것을 기하학적으로 보여줄 수 있다.
x → x − δ θ × x . {\displaystyle \mathbf {x} \rightarrow \mathbf {x} -\mathsymbol {\theta}}\mathbf {x} 따라서 우리는 극소수의 회전도 기대할 수 있다.
U ( R ( δ θ ) ) f ( x ) = f ( x − δ θ × x ) = f ( x ) − ( δ θ × x ) ⋅ ∇ f . {\displaystyle U(R(\delta {\boldsymbol {\theta }}))f(\mathbf {x} )=f(\mathbf {x} -\delta {\boldsymbol {\theta }}\times \mathbf {x} )=f(\mathbf {x} )-(\delta {\boldsymbol {\theta }}\times \mathbf {x} )\cdot \nabla f. } 그 뒤를 잇는다.
U ( R ( δ θ ) ) = 1 − ( δ θ × x ) ⋅ ∇ . {\displaystyle U(\delta \mathbf {\theta } )=1-(\delta \mathbf {\deta }\times \mathbf {x}\cdot \nabla .} 위와 같은 지수화 절차를 거쳐, 위치 기준으로 회전 연산자에 도달하는데, 이는 지수화된 방향 파생 모델이다.[12]
U ( R ( θ ) ) = 생략하다 ( − ( θ × x ) ⋅ ∇ ) . {\displaystyle U(R(\mathbf {\theta } )=\ex(\mathbf {\theta } \time \mathbf {x} )\cdot \nabla. } 정상파생상품 정상 파생상품 은 우주의 일부 표면으로 정규 방향(직교 )으로 취하거나, 일반적으로 일부 초저면 에 직교하는 정상 벡터장 을 따라 취해지는 방향 파생상품이다. Neumann 경계 조건 예를 참조하십시오. 정상 방향이 n {\ displaystyle \mathbf {n f 의 정상 파생 모델은 f {\ displaystyle {\frac {\partial }{\partial \mathbf{n}}}}}} .
∂ f ∂ n = ∇ f ( x ) ⋅ n = ∇ n f ( x ) = ∂ f ∂ x ⋅ n = D f ( x ) [ n ] . {\displaystyle {\frac {\partial f}{\partial \mathbf {n} }}=\nabla f(\mathbf {x} )\cdot \mathbf {n} =\nabla _{\mathbf {n} }{f}(\mathbf {x} )={\frac {\partial f}{\partial \mathbf {x} }}\cdot \mathbf {n} =Df(\mathbf {x} )[\mathbf {n} ]. } 고체의 연속 역학에서 연속체 역학의 몇 가지 중요한 결과는 벡터에 관한 벡터의 파생상품과 벡터와 텐더에 관한 텐서 의 파생상품이 필요하다.[13] 방향지시 는 이러한 파생상품을 찾는 체계적인 방법을 제공한다.
참고 항목 메모들 ^ R. Wrede; M.R. Spiegel (2010). Advanced Calculus (3rd ed.). Schaum's Outline Series. ISBN 978-0-07-162366-7 ^ 적용가능성은 측정기준 이 없는 공간에 걸친 기능 및 일반 상대성 처럼 서로 다른 다양성 에까지 확장된다. ^ 도트 제품이 정의되지 않은 경우 구배 도 정의되지 않지만, 구별 가능한 f 의 경우 방향 파생 모델이 여전히 정의되며, 외부 파생 모델과 유사한 관계가 존재한다. ^ 토마스, 조지 B. 주니어, 그리고 피니, 로스 L. (1979) 미적분 및 분석 기하학 , 애디슨-웨슬리 푸블리. 5번째 판 593페이지 ^ 이것은 일반적으로 유클리드 공간 을 가정한다. 예를 들어, 여러 변수의 함수는 일반적으로 벡터의 크기, 즉 단위 벡터의 크기에 대한 정의를 가지고 있지 않다. ^ Hughes Hallett, Deborah ; McCallum, William G. ; Gleason, Andrew M. (2012-01-01). Calculus : Single and multivariable . John wiley. p. 780. ISBN 9780470888612 OCLC 828768012 .^ Zee, A. (2013). Einstein gravity in a nutshell . Princeton: Princeton University Press. p. 341. ISBN 9780691145587 ^ Weinberg, Steven (1999). The quantum theory of fields ISBN 9780521550017 ^ Zee, A. (2013). Einstein gravity in a nutshell . Princeton: Princeton University Press. ISBN 9780691145587 ^ Cahill, Kevin Cahill (2013). Physical mathematics (Repr. ed.). Cambridge: Cambridge University Press. ISBN 978-1107005211 ^ Edwards, Ron Larson, Robert, Bruce H. (2010). Calculus of a single variable (9th ed.). Belmont: Brooks/Cole. ISBN 9780547209982 ^ Shankar, R. (1994). Principles of quantum mechanics (2nd ed.). New York: Kluwer Academic / Plenum. p. 318. ISBN 9780306447907 ^ J. E. 마스덴과 T. J. R. 휴즈, 2000년 탄력의 수학 재단 도버
참조 외부 링크 방향성 파생상품 관련 매체
![]() 위키미디어 커먼스의 방향성 파생상품 관련 매체
위키미디어 커먼스의 방향성 파생상품 관련 매체 








 (는)
(는) 



















![{\displaystyle (1+\delta '\cdot D)(1+\delta \cdot D)S^{\rho }-(1+\delta \cdot D)(1+\delta '\cdot D)S^{\rho }=\sum _{\mu ,\nu }\delta '^{\mu }\delta ^{\nu }[D_{\mu },D_{\nu }]S_{\rho }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16bc9cd9d4bae49561e46e2bb1ade2f241a21595)
![{\displaystyle [D_{\mu },D_{\nu }]S_{\rho }=\pm \sum _{\sigma }R^{\sigma }{}_{\rho \mu \nu }S_{\sigma },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32da9ce5c5713758361d02d266530759354ec070)






![{\displaystyle [1+\varepsilon \,(d/dx)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1af787ff07e53b33609086c1888d2b2fd239ced)

 (는) 극소수 변위 ε을 따라가는 방향 파생물이다. 우리는 번역 연산자의 최소 버전을 찾았다.
(는) 극소수 변위 ε을 따라가는 방향 파생물이다. 우리는 번역 연산자의 최소 버전을 찾았다. 


![{\displaystyle [U({\boldsymbol {\varepsilon }})]^{N}=U(N{\boldsymbol {\varepsilon }})=U({\boldsymbol {\lambda }}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0bf68a8ddea4b223e57aeb96125b6b252ef9974)
![{\displaystyle [U({\boldsymbol {\varepsilon }})]^{N}=\left[1+{\boldsymbol {\varepsilon }}\cdot \nabla \right]^{N}=\left[1+{\frac {{\boldsymbol {\lambda }}\cdot \nabla }{N}}\right]^{N}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5cb18356a03f1395fb84f7ae1a1969aaa05896b)
![{\displaystyle \exp(x)=\left[1+{\frac {x}{N}}\right]^{N},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72cd3c66555f47bbb7bb2894720f878de7e958df)
![{\displaystyle [U({\boldsymbol {\varepsilon }})]^{N}f(\mathbf {x} )=f(\mathbf {x} +N{\boldsymbol {\varepsilon }})=f(\mathbf {x} +{\boldsymbol {\lambda }})=U({\boldsymbol {\lambda }})f(\mathbf {x} )=\exp \left({\boldsymbol {\lambda }}\cdot \nabla \right)f(\mathbf {x} ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d948442f3d9aeed6f9ffcca821983b35f7a11f5d)








 정의상 그 지수에서 대칭이므로, 우리는 다음과 같은
정의상 그 지수에서 대칭이므로, 우리는 다음과 같은 ![{\displaystyle [t_{b},t_{c}]=i\sum _{a}(-f^{abc}+f^{acb})t_{a}=i\sum _{a}C^{abc}t_{a},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d682fb34fea7e6e3db932ef59372745c8e7bc54b)
![{\displaystyle \left[{\frac {\partial }{\partial x^{b}}},{\frac {\partial }{\partial x^{c}}}\right]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfdf13b5bcc7ed6bd7e78c471510e16087a8cc2d)











![{\displaystyle {\frac {\partial f}{\partial \mathbf {n} }}=\nabla f(\mathbf {x} )\cdot \mathbf {n} =\nabla _{\mathbf {n} }{f}(\mathbf {x} )={\frac {\partial f}{\partial \mathbf {x} }}\cdot \mathbf {n} =Df(\mathbf {x} )[\mathbf {n} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a4f10487f6111dbab2f9d600d023737d01899fe)
![{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd4359c84cf58e41375f33503df17f688456372)




![{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b946f4d0b2712f1f6b890f4b5b45a2bb70b7c7)







![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97c637955623ac4900c4f80d6ea1bdef354076a)





![{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c53f2457fa27a03ca72cbd48debb1255593088)






