리만 표면
Riemann surface수학, 특히 복소해석학에서 리만 표면은 연결된 1차원 복소다양체이다.이 표면들은 Bernhard Riemann에 의해 처음 연구되었고 이름을 따왔다.리만 표면은 복잡한 평면의 변형된 버전으로 생각할 수 있습니다. 모든 점 근처에서 그것들은 복잡한 평면의 패치처럼 보이지만, 글로벌 위상은 상당히 다를 수 있습니다.예를 들어, 그것들은 구체, 토러스 또는 여러 장의 시트가 함께 접착된 것처럼 보일 수 있습니다.
리만 표면의 주된 관심사는 그 사이에 정칙함수가 정의될 수 있다는 것이다.리만 표면은 오늘날 이러한 함수, 특히 제곱근과 다른 대수 함수 또는 로그와 같은 다치 함수의 전역 동작을 연구하기 위한 자연스러운 설정으로 여겨진다.
모든 리만 표면은 2차원 실해석 다양체(즉, 표면)이지만, 홀모픽 함수의 명확한 정의에 필요한 더 많은 구조(특히 복잡한 구조)를 포함하고 있다.2차원 실다양체는 방향성 및 측정이 가능한 경우에만 (보통 몇 가지 부등식 방식으로) 리만 표면으로 변할 수 있다.구체와 토러스는 복잡한 구조를 받아들이지만, 뫼비우스 스트립, 클라인 병, 그리고 실제 투영 평면은 그렇지 않습니다.
리만 표면에 대한 기하학적 사실은 가능한 한 "나이스"이며, 그것들은 종종 다른 곡선, 다양체 또는 다양체에 대한 일반화를 위한 직관과 동기를 제공한다.리만-로흐 정리가 이 영향의 대표적인 예이다.
정의들
리만 표면에는 몇 가지 동등한 정의가 있다.
- 리만 표면 X는 복소 차원 1의 연결된 복합 다양체이다.이는 X가 복잡한 평면의 열린 단위 디스크에 차트 아틀라스를 부여한 연결된 하우스도르프 공간임을 의미한다. 모든 점 x δ X에 대해 복합 평면의 열린 단위 디스크와 동형인 x 근방이 존재하며, 두 겹치는 차트 간의 전이 맵이 홀모픽이어야 한다.
- 리만 표면은 등각 구조와 함께 (실제) 치수 2 – 양면 표면 -의 지향성 다양체이다.다시, 다양체는 X의 임의의 점 x에서 국소적으로 공간이 실제 평면의 부분 집합과 동형임을 의미합니다.보충물 "리만"은 X가 다양체에서 각도를 측정할 수 있는 추가 구조, 즉 소위 리만 메트릭의 등가 등급을 부여받았다는 것을 의미한다.그러한 두 가지 지표는 측정한 각도가 동일한 경우 동일한 것으로 간주된다.X에서 메트릭의 동등성 클래스를 선택하는 것은 적합 구조의 추가 기준입니다.
복소구조는 복소평면에 주어진 표준 유클리드 메트릭을 선택하고 차트를 통해 X로 전송함으로써 등각구조를 일으킨다.등각 구조가 복잡한 구조를 결정한다는 것을 보여주는 것은 더 어렵다.[1]
예
- 복소 평면 C는 가장 기본적인 리만 표면이다.지도 f(z) = z(ID 맵)는 C에 대한 차트를 정의하고 {f}은 C에 대한 지도책입니다.지도 g(z) = z*(공역 지도)도 C에 대한 차트를 정의하고 {g}은 C에 대한 지도입니다.차트 f와 g는 호환되지 않으므로 C는 두 개의 서로 다른 리만 표면 구조를 가질 수 있습니다.사실, 리만 표면 X와 그 지도책 A가 주어졌을 때, 켤레 지도책 B = {f* : f δ A}는 결코 A와 양립할 수 없으며, X는 구별되고 양립할 수 없는 리만 구조를 가질 수 있다.
- 유사한 방법으로, 복소 평면의 비어 있지 않은 모든 열린 부분 집합은 자연스러운 방법으로 리만 표면으로 볼 수 있다.보다 일반적으로, 리만 표면의 비어 있지 않은 모든 열린 부분 집합은 리만 표면이다.
- S = C ∪ {disc}로 하고 f(z) = z로 합니다. 여기서 z는 S \ {disc}이고 g(z) = 1/z는 S \ {0}이고 1/disc는 0으로 정의됩니다.f와 g는 차트이고 양립가능하며 {f, g }는 S의 지도책으로 S를 리만 표면으로 만든다.이 특별한 표면은 복잡한 평면을 구 주위에 감싸는 것으로 해석될 수 있기 때문에 리만 구라고 불립니다.복잡한 평면과 달리 컴팩트합니다.
- 콤팩트 리만 표면의 이론은 복소수 및 비단수적으로 정의된 투영 대수 곡선의 이론과 동등하다는 것을 보여줄 수 있다.예를 들어 torusC/(Z + θ Z)는 여기서 θ가 복소수 비실수이며 격자Z + θZ와 관련된 바이어스트라스 타원함수를 통해 방정식에 의해 주어진 타원곡선에 대응한다.
- y2 = x3 + a x + b.
Tori는 속1의 유일한 리만 표면이며, 보다 높은 속g의 표면은 과피질 표면에 의해 제공된다.
- y2 = P(x),
- 콤팩트 리만 표면은 C n \에 포함될 수 있기 때문에 대수 곡선입니다.이것은 Kodaira 임베딩 정리 및 모든 복잡한 [2]곡선에 양의 선다발이 존재한다는 사실에서 비롯된다.
- 비콤팩트 리만 표면의 중요한 예는 분석 연속에 의해 제공된다.
추가 정의 및 속성
복소다양체 사이의 다른 지도와 마찬가지로, 2개의 리만 표면 M과 N 사이의 함수 f:M → N은 M의 아틀라스 내의 모든 차트 g와 N의 아틀라스 내의 모든 차트 h에 대해 정의된 모든 맵 h θ f θ−1 g가 (C에서 C로의 함수로서) 홀모형이라고 불린다.두 개의 정형 지도의 구성은 정형이다.2개의 리만 표면 M과 N은 M에서 N까지 역순사적 정형함수가 존재한다면 바이홀로포머(또는 등가적으로 등가)라고 불린다(후자 조건은 자동이므로 생략할 수 있다.두 개의 등가 리만 표면은 실질적으로 모두 동일하다.
방향성
각각의 리만 표면은 복잡한 다양체이며, 실제 다양체로서 방향을 잡을 수 있다.전이함수 h = f(g−1(z)인 복소수 f 및 g의 경우, h는 복소수 h'(z)의 곱셈에 의해 주어진 실선형 지도에 불과한 점 z의 야코비안 R에 대한 열린22 집합에서 R까지의 지도라고 볼 수 있다.그러나, 복소수 α에 의한 곱셈의 실제 행렬식은 α와 같으므로, h의 야코비안은 양의 행렬식을 가진다.따라서 복잡한 아틀라스는 지향성 아틀라스가 된다.
기능들
모든 비콤팩트 리만 표면은 (C의 값을 갖는) 비정수 홀모픽 함수를 허용한다.사실, 모든 비정밀 리만 표면은 스타인 다양체이다.
이와는 대조적으로 콤팩트 리만 표면 X에서는 C의 값을 갖는 모든 홀모픽 함수는 최대 원리로 인해 일정하다.그러나, 항상 일정하지 않은 meromific 함수(리만 구 C ∪ {}}의 값을 갖는 holomific 함수)가 존재한다.보다 정확하게는, X의 함수장은 C(t)의 유한 확장이며, 하나의 변수, 즉 임의의 두 개의 자형 함수는 대수적으로 의존합니다.이 문장은 더 높은 차원으로 일반화된다(Siegel(1955) 참조).메로모픽 함수는 리만 세타 함수와 표면의 아벨-야코비 지도의 관점에서 상당히 명시적으로 주어질 수 있다.
해석 대 대수
비정수적 다형함수의 존재는 콤팩트한 리만 표면이 투영적 다양성이라는 것을 보여주기 위해 사용될 수 있다. 즉, 투영적 공간 내의 다항식 방정식에 의해 주어질 수 있다.사실, 모든 콤팩트 리만 표면이 복잡한 투영 3 공간에 삽입될 수 있다는 것을 보여줄 수 있다.이것은 놀라운 정리입니다.리만 표면은 로컬 패치 차트에 의해 제공됩니다.만약 하나의 전역 조건, 즉 콤팩트함을 더한다면, 표면은 필연적으로 대수적이다.리만 표면의 이러한 특징은 해석적 또는 대수적 기하학적 방법으로 그것들을 연구할 수 있게 해준다.고차원 물체에 대한 해당 문장은 거짓이다. 즉, 대수적이지 않은 콤팩트 복합 2-매니폴드가 있다.반면에, 모든 투영 복소 다양체는 필연적으로 대수적입니다. Chow의 정리를 참조하십시오.
예를 들어 Torus T : = C/(Z + δ Z)를 예로 들 수 있다.격자 Z + δ Z에 속하는 Weierstrass 함수(z ) \ \_{\}(는 T 위의 meromaph 함수이다. 함수와 그 도함수 (( z) { \_{\}'(는 T의 함수 필드를 생성합니다.방정식이 있다.
여기서 계수2 g와3 g는 θ에 의존하며, 따라서 대수기하학의 의미에서 타원곡선τ E를 제공한다.이를 반전시키는 것은 j불변 j(E)에 의해 이루어지며, j불변 j(E)는 θ와 토러스를 결정하는 데 사용할 수 있다.
리만 표면의 분류
모든 리만 표면의 집합은 쌍곡선, 포물선 및 타원 리만 표면이라는 세 가지 하위 집합으로 나눌 수 있습니다.기하학적으로, 이러한 곡선은 음수, 소실 또는 양의 일정한 단면 곡률을 가진 표면에 해당합니다.즉, 연결된 모든 리만 X X는 -1, 0 11)과동일한 곡률을 갖는 고유한 완전한 2차원 실제 리만 메트릭을 허용합니다. 이 메트릭은 리만 표면으로서 구조에 따라 결정됩니다.이것은 등온 좌표의 결과로 볼 수 있다.
복소해석학 용어로, 푸앵카레-코에베 균등화 정리(리만 매핑 정리의 일반화)는 간단히 연결된 모든 리만 표면이 다음 중 하나와 일치한다고 기술한다.
- 리만 C : { { { } : \ { C \ \ { \ \ infty\} 、 () \ \ } { } ( \ { C; ) )
- 복소 C
- 열린 D : { C : < { : = \ \mathbf} : z < 1 이며, 이는 상부 H : { :() > { style \ } 에 해당합니다.
리만 표면은 범용 커버가 ( (\ C (\displaystyle D (\와 동형인지 여부에 따라 타원형, 포물형 또는 쌍곡선형입니다. 각 클래스에 더 많은 요소를 수용합니다.
타원 리만 표면
리만 1 ( )( \ displaystyle { P ^{{C )은 유일한 예시이다. 왜냐하면 자유롭고 적절하게 불연속적으로 바이홀로포맷 변환에 의해 작용되는 군(\mathbf C})은 존재하지 않으며, 따라서 범용 가 1 ( \ {1 {1} {1}}에 동형상인 리만 표면(\mathbf ^1}는, 그 자체가 동형이어야 합니다.
포물선 리만 표면
XX가 범용 커버가 C(\displaystyle {C와 동형인 리만 표면이라면 표면 중 하나와 동형입니다.
- 자체
- style \ /\의 비율;
- /(Z + )( \ \} / ( \ { + \ { } \ ) 여기서 C ( \ \ \ tau{ } 。
토폴로지적으로 평면, 실린더, 토러스 세 가지 유형만 있습니다.그러나 앞의 두 사례에서는 (포물선) 리만 표면 구조가 독특하지만, 세 번째 사례에서는 파라미터(\를 변경하면 비동형 리만 표면이 된다. style \에 의한 설명은 "표시된" 리만 표면의 테이크뮐러 공간을 제공합니다(리만 표면 구조 외에 토러스에 고정된 동형상으로 보일 수 있는 "표시"의 위상 데이터를 추가합니다).해석 모듈리 공간을 얻으려면(마킹을 생략) 매핑 클래스 그룹에 의한 테이크뮐러 공간의 몫이 필요합니다.이 경우 모듈러 곡선입니다.
쌍곡선 리만 표면
나머지 X X는 Fuchsian 그룹에 의한 상부 반평면의 비율과 동형인 쌍곡선 리만 표면이다(이것은 표면에 대해 Fuchsian 모델이라고도 불린다).유형은 토러스 및 구를 제외한 방향 지정 가능한 표면일 수 있습니다.
특히 X(\ X가 컴팩트한 입니다.그 후 위상유형은 g g2)로 기술되며, Teichmüler 공간과 모듈리 공간은 -(\ - 6이다.유한 유형의 리만 표면(닫힌 표면에서 유한한 수의 점을 뺀 것과 동형)에 대한 유사한 분류가 주어질 수 있다.그러나 일반적으로 무한 위상 유형의 리만 표면의 모듈리 공간이 너무 커서 그러한 설명을 수용할 수 없다.
리만 표면 간 지도
기하학적 분류는 Liouville의 정리와 Little Picard 정리에 자세히 나와 있듯이 리만 표면 사이의 지도에 반영되어 있습니다. 쌍곡선에서 포물선으로, 또는 포물선에서 쌍곡선으로의 지도는 매우 제약적입니다(실제로, 일반적으로 일정합니다!).구면에는 의 포함이 있습니다. , C, {\ \{\{\ 그러나 구면에서 평면까지의 모든 홀모픽 맵은 일정하며, 평면으로부터 원반 단위까지의 홀모형은 일정합니다.평면으로부터 평면까지의 phic 지도에서 2점을 뺀 것은 상수입니다(리틀 피카르 정리).
구멍이 뚫린 구
이러한 진술은 다수의 펑크가 있는 리만 C^(\mathbf {의 유형을 고려하여 명확해진다.구멍이 없는 것은 타원형인 리만 구면이다.무한대에 배치할 수 있는 하나의 천자로, 그것은 포물선인 복잡한 평면이다.두 개의 구멍이 있는 것은 구멍이 난 평면 또는 포물선인 고리 또는 실린더입니다.3개 이상의 펑크가 있는 경우, 쌍곡선입니다 – 바지 한 벌을 비교해 보십시오.지수 맵(전체이며 무한대에서 필수적인 특이점을 가지므로 무한대에서 정의되지 않고 0과 무한대를 놓침)을 통해 하나의 펑크에서 두 개로 매핑할 수 있지만, 0에서 한 개 또는 두 개 펑크에서 세 개 이상의 펑크로 매핑하는 모든 맵은 일정합니다.
라미네이트된 피복 공간
이 맥락에서, 콤팩트한 리만 표면은 하위 속 표면에는 매핑할 수 있지만 상수 맵을 제외하고 상위 속에는 매핑할 수 없다.이는 홀모픽 및 자형 맵이 zz n, {\}처럼 국소적으로 작용하기 때문에 비정수 맵은 덮개 맵으로 라미네이트되고 콤팩트 리만 표면의 경우 리만-에 의해 구속되기 때문이다.공간 및 라미네이트 커버의 오일러 특성을 관련짓는 대수 위상의 후르비츠 공식.
예를 들어, 쌍곡선 리만 표면은 구체의 공간을 덮는 라미네이트이지만(비정수적인 자형함수를 가지지만), 구는 상수를 제외하고 더 높은 속 표면을 덮지 않거나 더 높은 속 표면으로 매핑되지 않습니다.
리만 표면의 등각도
균일화된 리만 표면의 등각군(등각 자기동형군)은 기하학을 반영한다.
- 0속 – 구체의 등각도 그룹은 복합 라인의 투영 변환의 뫼비우스 그룹이다.
- 평면의 등각도 그룹은 무한대를 고정하는 부분군이고, 펑크 평면의 부분군은 무한대와 0만을 포함하는 집합을 불변하게 남기는 부분군이다. 즉, 둘 다 고정하거나 교환(1/z)한다.
- 상부 반평면의 등각군은 실제 뫼비우스 군이며, 이는 디스크의 자기동형군과 공역한다.
- 1속 – 사각 격자와 육각 격자는 90°와 60° 회전으로부터 추가 대칭을 가지지만, 토러스의 등각군(Abelian variety)은 일반적인 번역(Abelian variety)이다.
- 속 g ≤ 2에 대하여, 등각군은 유한하며, 후르비츠의 자기동형정리에 의해 최대 84(g-1)의 차수를 가진다. 이 한계를 실현하는 표면을 후르비츠 표면이라고 한다.
- 모든 유한군은 일부 리만 [3]표면의 등각체의 전체 군으로 실현될 수 있다고 알려져 있다.
기능-이론
위의 분류 체계는 일반적으로 기하학에서 사용됩니다.일반적으로 복합 분석가가 사용하는 리만 표면에는 다른 분류가 있습니다.이것은 "포물선"과 "초과적"에 대해 다른 정의를 사용합니다.이 대체 분류 체계에서 리만 표면은 표면에 일정하지 않은 음의 하위 고조파 함수가 없으면 포물선이라고 하며, 그 외에는 [4][5]쌍곡선이라고 합니다.이러한 쌍곡면 클래스는 음의 하위 고조파 함수가 아닌 함수 공간이 퇴화되는지 여부에 따라 하위 클래스로 더욱 세분된다. 예를 들어, 모든 유계 홀모픽 함수가 일정하거나, 모든 유계 고조파 함수가 일정하거나, 또는 모든 양의 고조파 함수가 일정한 리만 표면는 상수 등입니다.
혼동을 피하기 위해 일정한 곡률의 메트릭에 기초한 분류를 기하학적 분류라고 하고, 함수공간의 축퇴에 기초한 분류를 함수이론 분류라고 한다.예를 들어, "0과 1을 제외한 모든 복소수"로 구성된 리만 표면은 함수-이론 분류에서는 포물선이지만 기하학적 분류에서는 쌍곡선이다.
「 」를 참조해 주세요.
리만 표면에 관한 이론
메모들
- ^ 대응하는 복잡한 구조의 구조에 대해서는 (Jost 2006, Ch. 3.11)을 참조해 주세요.
- ^ Nollet, Scott. "KODAIRA'S THEOREM AND COMPACTIFICATION OF MUMFORD'S MODULI SPACE Mg" (PDF).
- ^ Greenberg, L. (1974). "Maximal groups and signatures". Discontinuous Groups and Riemann Surfaces: Proceedings of the 1973 Conference at the University of Maryland. Ann. Math. Studies. Vol. 79. pp. 207–226. ISBN 0691081387.
- ^ Ahlfors, Lars; Sario, Leo (1960), Riemann Surfaces (1st ed.), Princeton, New Jersey: Princeton University Press, p. 204
- ^ Rodin, Burton; Sario, Leo (1968), Principal Functions (1st ed.), Princeton, New Jersey: D. Von Nostrand Company, Inc., p. 199, ISBN 9781468480382
레퍼런스
- Farkas, Hershel M.; Kra, Irwin (1980), Riemann Surfaces (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-90465-8
- 파블로 아레스 가스테시, 리만 서피스북
- Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157, OCLC 13348052(특히 IV장).
- Jost, Jürgen (2006), Compact Riemann Surfaces, Berlin, New York: Springer-Verlag, pp. 208–219, ISBN 978-3-540-33065-3
- Papadopoulos, Athanase, ed. (2007), Handbook of Teichmüller theory. Vol. I, IRMA Lectures in Mathematics and Theoretical Physics, vol. 11, European Mathematical Society (EMS), Zürich, doi:10.4171/029, ISBN 978-3-03719-029-6, MR 2284826, S2CID 119593165
- Lawton, Sean; Peterson, Elisha (2009), Papadopoulos, Athanase (ed.), Handbook of Teichmüller theory. Vol. II, IRMA Lectures in Mathematics and Theoretical Physics, vol. 13, European Mathematical Society (EMS), Zürich, arXiv:math/0511271, doi:10.4171/055, ISBN 978-3-03719-055-5, MR 2524085, S2CID 16687772
- Papadopoulos, Athanase, ed. (2012), Handbook of Teichmüller theory. Vol. III, IRMA Lectures in Mathematics and Theoretical Physics, vol. 19, European Mathematical Society (EMS), Zürich, doi:10.4171/103, ISBN 978-3-03719-103-3
- *Remmert, Reinhold (1998). "From Riemann Surfaces to Complex Spaces". Séminaires et Congrès. Zbl 1044.01520.
- Siegel, Carl Ludwig (1955), "Meromorphe Funktionen auf kompakten analytischen Mannigfaltigkeiten", Nachrichten der Akademie der Wissenschaften in Göttingen. II. Mathematisch-Physikalische Klasse, 1955: 71–77, ISSN 0065-5295, MR 0074061
- Weyl, Hermann (2009) [1913], The concept of a Riemann surface (3rd ed.), New York: Dover Publications, ISBN 978-0-486-47004-7, MR 0069903
외부 링크
- "Riemann surface", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- McMullen, C. "Complex Analysis on Riemann Surfaces Math 213b" (PDF). Harvard Math. Harvard University.




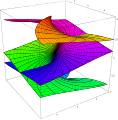

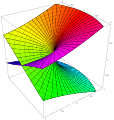


 T 위의
T 위의  T의 함수 필드를 생성합니다.방정식이 있다.
T의 함수 필드를 생성합니다.방정식이 있다.![{\displaystyle [\wp '(z)]^{2}=4[\wp (z)]^{3}-g_{2}\wp (z)-g_{3},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d094adcb0b3a44c6e5cbdc747eef133ab81f4d67)
 -1, 0
-1, 0








 변경하면 비동형 리만 표면이 된다.
변경하면 비동형 리만 표면이 된다.
 .유한 유형의 리만 표면(닫힌 표면에서 유한한 수의 점을 뺀 것과 동형)에 대한 유사한 분류가 주어질 수 있다.그러나 일반적으로 무한 위상 유형의 리만 표면의 모듈리 공간이 너무 커서 그러한 설명을 수용할 수 없다.
.유한 유형의 리만 표면(닫힌 표면에서 유한한 수의 점을 뺀 것과 동형)에 대한 유사한 분류가 주어질 수 있다.그러나 일반적으로 무한 위상 유형의 리만 표면의 모듈리 공간이 너무 커서 그러한 설명을 수용할 수 없다. 
 유형을 고려하여 명확해진다.구멍이 없는 것은 타원형인 리만 구면이다.무한대에 배치할 수 있는 하나의 천자로, 그것은 포물선인 복잡한 평면이다.두 개의 구멍이 있는 것은 구멍이 난 평면 또는 포물선인 고리 또는 실린더입니다.3개 이상의 펑크가 있는 경우, 쌍곡선입니다 – 바지 한
유형을 고려하여 명확해진다.구멍이 없는 것은 타원형인 리만 구면이다.무한대에 배치할 수 있는 하나의 천자로, 그것은 포물선인 복잡한 평면이다.두 개의 구멍이 있는 것은 구멍이 난 평면 또는 포물선인 고리 또는 실린더입니다.3개 이상의 펑크가 있는 경우, 쌍곡선입니다 – 바지 한 


