봉투(수학)

기하학에서, 곡선의 평면 계열의 봉투는 어느 시점에서 가족의 각 구성원과 접하는 곡선이며, 이러한 접선의 점들이 함께 전체 봉투를 형성한다. 고전적으로 봉투의 한 점은 인근 곡선의 교차점 한계를 의미하는 두 개의 "적외선 인접" 곡선의 교차점이라고 생각할 수 있다. 이 아이디어는 우주 표면의 봉투에 일반화될 수 있으며, 더 높은 차원에도 일반화될 수 있다.

봉투가 있으려면 접선 개념을 달리 적용하지 않고, 구성원을 통한 원활한 전환이 이루어져야 하므로 곡선 계열의 개별 구성원이 서로 다른 곡선을 그릴 필요가 있다. 그러나 이러한 조건으로는 충분하지 않다. 주어진 가족이 봉투를 갖지 못할 수도 있다. 이것의 간단한 예는 확장 반지름의 동심원 가족에 의해 제시된다.

곡선 계열의 봉투

패밀리의 각 곡선 C를_t 방정식 f_t(x, y)=0(암묵적 곡선 참조)의 해법으로 주도록 한다. 여기서 t는 매개변수다. F(t, x, y)=f_t(x, y)라고 쓰고 F가 다를 수 있다고 가정한다.

그런_t 다음 C 패밀리의 엔벨롭을 $D{\displaystyle \mathcal{}}$ ${\$ 포인트(x,y)의$$ 집합으로 정의한다.

${\displaystyle F(t,x,y)=0~{\mathsf{and}~{\partial F \over \partial t}(t,x,y)=0}$

t의 일부 값에 대해, ${\displaystyle \mathrm{여기}}$서 $\partial {\displaystyle \mathrm{}}$ F${\displaystyle }$/ ${\displaystyle \partial \mathrm{}}$ ${\displaystyle t}$ ${\displaystyle \partial F/\partial t}$은 t에 대한 F의 부분 파생 모델이다.^[1]

t와 u, t≠u가 모수의 두 값이면 C와_t C의_u 교차점은 다음과 같이 주어진다.

${\displaystyle F(t,x,y)=F(u,x,y)=0\,}$

또는 동등하게

${\displaystyle F(t,x,y)=0~{{\mathsf {and}~{\frac {F(u,x,y)-F(t,x,y)}{u-t}=0.}$

u → t가 위의 정의를 내리도록 한다.

중요한 특별한 경우는 F(t, x, y)가 t 단위의 다항식인 경우다. 여기에는 분모를 삭제함으로써 F(t, x, y)가 t에서 합리적인 함수인 경우를 포함한다. 이 경우 정의는 F(t, x, y)의 이중 근원이므로 (정의가 일부 t에서는 F=0을 요구하고 첫 번째 파생상품 =0을 요구하기 때문에) F(t, x, y)의 차별성을 0으로 설정하면 봉투의 방정식을 찾을 수 있다.

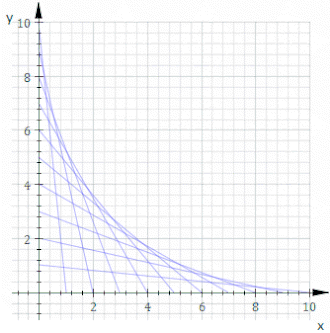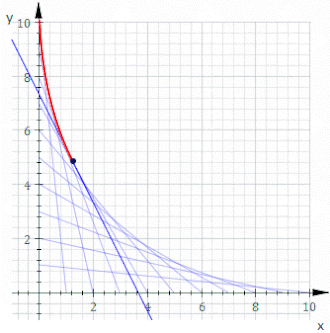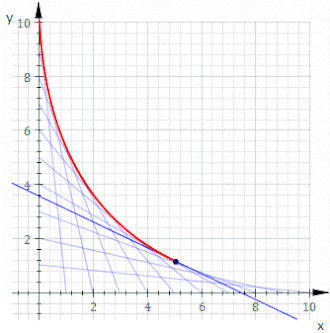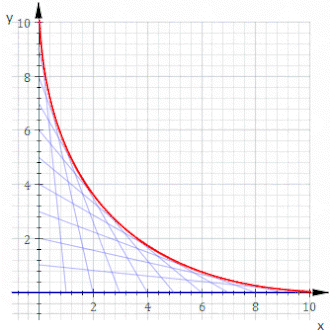
예를 들어, X와 Y 가로채기가 t와 11-t인 선이 C로_t 하자. 위의 애니메이션에 나와 있다. C의_t 방정식은

${\displaystyle {\frac {x}{t}+{\frac {y}{11-t}=1}$

또는, 분수를 치우는 것,

${\displaystyle x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,}$

그 봉투의 방정식은 그때다.

${\displaystyle(-x+y-11)^{2}-44x=(x-y)^{2}-22(x+y)+0.\,}$

종종 F가 매개변수의 합리적인 함수가 아닌 경우 적절한 대체에 의해 이 경우로 축소될 수 있다. 예를 들어, cos u(x, y)cos θ+v(x, y)cos θ=w(x, y)sin θ=w(x, y)=w(t+1/t)/2, sin θ=(t-1/t)/2i 등의 방정식을 C에_θ 의해 주어지는 경우, courcos^iθ ==(cos)=(t-1/t)/i)/2i를 사용하여 곡선의 방정식을 변경한다.

${\displaystyle u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t}=w}$

또는

${\displaystyle (u-iv)t^{2}-2wt+(u+iv)=0.\,}$

그런 다음 차별을 0으로 설정하여 봉투의 방정식을 제공한다.

${\displaystyle (u-iv)(u+iv)-w^{2}=0\,}$

또는

${\displaystyle u^{2}+v^{2}}}=w^{2}.\,}$

대체 정의

1. E번₁ 봉투는 인근_t C곡선의 교차점 한계다.
2. E₂ 봉투는 C의_t 모든 부분에 접하는 곡선이다.
3. E 봉투는₃ C_t 곡선으로 채워진 영역의 경계선이다.

Then ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$, ${\displaystyle E_{2}\subseteq {\mathcal {D}}}$ and ${\displaystyle E_{3}\subseteq {\mathcal {D}}}$, where ${\displaystyle {\mathcal {D}}}$ is the set of points defined at the beginning of this subsection's parent sect이온의

예

예 1

봉투의 이러한 정의 E₁, E₂ 및 E는₃ 서로 다른 집합일 수 있다. 예를 들어, γ : R → R에² 의해 매개변수화된 y = x를³ 고려하십시오. 여기서 γ(t) = (t,t³). 1-모수 곡선군은 접선 선으로 γ에 주어진다.

먼저 판별 $D{\displaystyle \mathcal{}}$ ${\$을(를) 계산한다$.$ 생성함수는

${\displaystyle F(t, (x,y)=3t^{2}x-y-2t^{3}.}$

부분파생상품 F_t = 6t(x – t) 계산. 그 뒤에 x = t 또는 t = 0이 있다. 먼저 x = t와 t ≠ 0으로 대체한다고 가정한다. F: $F{\displaystyle (t,}$ (${\displaystyle t,}$ y${\displaystyle }$)${\displaystyle }$= t ${\displaystyle 3{}^{}}$- y ${\$ 따라서$$ t ≠ 0으로 가정하면 F = 0이고_t (x,y) = (t, t³)일 경우에만 F = 0으로 바뀐다. 다음으로 t = 0이라고 가정하고 F로 대체하면 F(0, (x,y) = -y가 된다. 따라서 t = 0이라고 가정하면 F = F_t = 0인 경우, y = 0인 경우에만 그 뒤를 따른다. 따라서 판별은 원래 곡선이고 γ(0)에서 접선이다.

${\displaystyle {\d}=\{(x,y)\in \mathb {R}^{2}:y=x^{3}\cup \{(x,y)\in \mathb {R}^{2}:y=0\\\}$

다음으로 우리는₁ E를 계산한다. 하나의 곡선은 F(t, (x,y) = 0으로, 근처 곡선은 F(t + ε, (x,y)로 주어진다. 여기서 ε은 매우 작은 숫자다. 교차로점은 ε이 0이 되는 경향이 있기 때문에 F(t, (x,y) = F(t + ,, (x,y))의 한계를 보는 데서 온다. F(t, (x,y) = F(t + ε, (x,y))는 다음의 경우에 한함

${\displaystyle L:=F(t,)(x,y)-F(t+\varepsilon ,)(x,y)=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon)=0.}$

t ≠ 0이면 L은 ε의 단일 계수만을 가진다. t ≠ 0이라고 가정할 때 교차점은 다음과 같다.

${\displaystyle \lim _{\barepsilon \to 0}{\frac {1}{\barepsilon }L=6t(t-x)\ .}$

t ≠ 0이므로 x = t를 따른다. y 값은 이 점이 원래 곡선 γ에 접선선에 있어야 한다는 것을 알고 계산한다: F(t, (x,y) = 0. 대체와 해결은 y = t를³ 준다. t = 0일 때 L은 ε으로² 나누어진다. t = 0이라고 가정할 때, 교차는 다음과 같이 주어진다.

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}L=3x\ .}$

그 다음 x = 0이며, F(t, (x,y) = 0을 알면 y = 0이 된다. 그 뒤를 잇는다.

$\displaystyle E_{1}=\{(x,y)\in \mathb {R}^{2}:y=x^{3}\}\}$

다음으로 우리는₂ E를 계산한다. 곡선 자체는 자신의 모든 접선 선에 접하는 곡선이다. 그 뒤를 잇는다.

$\displaystyle E_{2}=\{(x,y)\in \mathb {R}^{2}:y=x^{3}\}\}$

마침내 우리는₃ E를 계산한다. 평면의 모든 점에는 그것을 통과하는 γ에 적어도 하나의 접선선이 있으며, 따라서 접선선에 의해 채워진 부위는 전체 평면이다. 따라서 경계 E는₃ 빈 집합이다. 실제로, (x₀,y₀)라고 말하면, 비행기의 한 점을 고려해보라. 이 점은 다음과 같은 t가 존재하는 경우에만 접선선에 있다.

${\displaystyle F(t, (x_{0},y_{0})=3t^{2}x_{0}-y_{0}-{0}-2t^{3}=0\}$

이것은 t의 세제곱이며, 따라서 적어도 하나의 실제 용액이 있다. γ에 대한 최소 하나의 접선선이 평면의 주어진 지점을 통과해야 한다는 것을 따른다. y > x와³ y > 0이면, 각 점(x,y)은 그것을 통과하는 γ에 정확히 하나의 접선선을 가진다. y < x y³ < 0>도 마찬가지다. y < x와³ y > 0일 경우, 각 점(x,y)은 그것을 통과하는 γ에 대해 정확히 세 개의 뚜렷한 접선 선을 가진다. y > x와³ y < 0도 마찬가지다. y = x와³ y ≠ 0인 경우, 각 점(x,y)은 이를 통과하는 to에 정확히 두 개의 접선선을 가진다(이것은 입방체에 하나의 보통근과 하나의 반복된 근을 갖는 것에 해당한다). y ≠ x와³ y = 0인 경우에도 마찬가지다. y = x와³ x = 0, 즉 x = y = 0인 경우, 이 점은 이를 통과하는 γ에 대한 단일 접선선을 가진다(이는 입방체에 복수성 3의 하나의 실제 루트를 갖는 것에 해당한다). 그 뒤를 잇는다.

${\displaystyle E_{3}=\varnothing.}$

예 2

스트링 아트에서는 동일한 간격으로 두 줄을 교차 연결하는 것이 일반적이다. 어떤 곡선이 형성되는가?

단순성을 위해 x축과 y축에 핀을 설정하십시오. 비직교 레이아웃은 회전 및 스케일링입니다. 일반 직선 스레드는 두 점(0, k-t)과 (t, 0)을 연결하는데, 여기서 k는 임의 스케일링 상수이며, 매개변수 t를 변화시켜 선의 패밀리가 생성된다. 단순한 기하학에서 이 직선의 방정식은 y = -(k - t)x/t + k - t. F(x,y,t) = 0 형식에서 재배열 및 주조는 다음을 제공한다.

${\displaystyle F(x,y,t)=-{\frac {kx}{t}-t+x+k-y=0\,}$

(1)

이제 t에 대해 F(x,y,t)를 구별하고 결과를 0으로 설정하여

${\displaystyle {\frac {\partial F(x,y,t)}{\partial t}={\frac {kx}{t^{2}}-1=0\,}$

(2)

이 두 방정식은 봉투의 방정식을 공동으로 정의한다. (2)에서 다음 사항을 확인하십시오.

${\displaystyle t={\sqrt {kx}\,}$

이 t 값을 (1)로 대체하고 단순화하는 것은 봉투에 대한 방정식을 제공한다.

${\displaystyle y=({\sqrt{x}-{\sqrt{k}})^{2}\,}$

(3)

또는 x와 y의 대칭을 보여주는 보다 우아한 형태로 재배열:

${\displaystyle {\sqrt{x}+{\sqrt {y}={\sqrt{k}}}$

(4)

b축이 y=x 북동쪽 선이고 축이 y=x 남동쪽 선인 축을 회전시킬 수 있다. 이 새로운 축들은 x=(b+a)/√2 및 y=(b-a)/√2에 의한 원래의 x-y 축과 관련이 있다. 우리는 (4)로 대체하고 확장 및 단순화 후,

${\displaystyle b}$= ${\displaystyle \frac{1k}{}}$ ${\displaystyle \frac{2\sqrt{\mathrm{}}}{}}$ a ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle \frac{k\mathrm{}}{}}$ ${\displaystyle \frac{2\sqrt{\mathrm{}}}{}}$ ${\$ b$={\frac {1}{k{\sqrt{2}}:a^{2}+{\frac {k}{{\sqrt{2$

(5)

이것은 명백히 a=0 또는 y=x를 따라 축이 있는 포물선의 방정식이다.

예 3

I ⊂ R을 개방간격으로 하고 γ : I → R을² 호 길이로 파라메트된 매끄러운 평면 곡선으로 한다. γ(I)에 대한 정규선의 1-모수 계열을 고려한다. 선은 γ(t)를 통과하고 γ(t)에서 접선 벡터에 수직인 경우 t(t)에서 γ에 정상이다. T는 단위 접선 벡터를 γ으로 나타내고 N은 단위 정규 벡터를 나타낸다. 점을 사용하여 도트 제품을 나타냄으로써, 정상 라인의 1-모수 계열에 대한 생성 패밀리는 F : I × R² → R에 의해 주어진다.

${\displaystyle F(t,{\mathbf {x}}}}=({\mathbf {x}-\gamma(t)\cdot {\mathbf {}(t)\mathbf {}\}$

분명히 (x - γ)/T = 0은 x - γ이 T에 수직인 경우에만, 또는 x - γ이 N에 평행한 경우에만, 또는 일부 λ R에 대해 x = γ + λN인 경우에만 동등하게. 그 뒤를 잇는다.

${\displaystyle L_{t_{0}}:=\\{{\mathbf {x} }\in \mathb {R} ^{2}:F(t_{0},{\mathbf {x}}}=0\}})$

γ(t₀)에서 γ까지의 정규선이다. F의 차별성을 찾으려면 t:에 대한 부분파생상품을 계산해야 한다.

${\displaystyle {\frac {\partial f}{\partial t}}(t, {\mathbf {x}}}}}}=\kappa(t)({\mathbf {x}-\gamma(t))\cdot {\mathbf {}{}(t)-1\},},},},}$

여기서 κ은 γ의 평면 곡선 곡면이다. 일부 λ ∈ R에 대해 x - γ = λN인 경우에만 F = 0인 것으로 간주되었다. F = 0인 경우를 가정하면 F = 0은 다음과 같다.

${\displaystyle {\frac {\partial f}{\partial t}=\lambda \kappa(t)-1\ .}$

κ 0 0이라고 가정하면 1 = 1/κ 등을 따른다.

${\displaystyle {\mathcal {D}=\gamma(t)+{\frac {1}{\kappa(t)}{\mathbf {}{{{}(N})(t)\ .}$

이것은 정확히 γ곡선의 회피다.

예 4

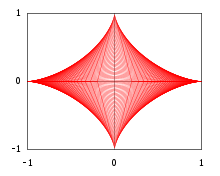
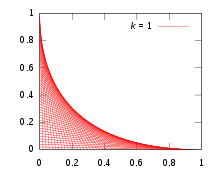
다음의 예는 어떤 경우에 곡선 계열의 봉투가 봉투의 곡선인 집합 조합의 토폴로지 경계로 보일 수 있다는 것을 보여준다. > ${\displaystyle s>0}$ 및 > 0 ${\displaystyle t>0}$의 경우 정점${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 0}$ ) ${\displaystyle (0,0)$,${\displaystyle (,}$ ${\displaystyle 0}$${\displaystyle }$) ${\displaystyle$(${\displaystyle s}$$,0)$ 및 ${\displaystyle (,}$ t${\displaystyle )}$ ${\displaystystyle (0,$ t$)})$가 있는 데카르트 평면의 (0, t)를 고려한다.

${\displaystyle T_{s,t}:=\\왼쪽\{(x,y)\in \mathb {R} _{+}^{2}:\\\\frac {x}{s}}+{\frac {y}{t}}}}<1\right\}}.}$

지수 > ${\displaystyle \alpha >0}$을를) 고정하고, s ${\displaystyle {\alpha }^{}}$+ ${\displaystyle \mathrm{t\alpha }{}^{}}$= 1 ${\$}=1}의 구속조건에$$ 따른 모든 $삼각형{\displaystyle {}_{}}$ T ${\displaystyle {s,}_{}}$ ${\displaystyle t_{}}$ ${\\$, t_s,$$t=1$}$의 결합을 고려한다$.$

${\displaystyle \Delta _{\alpha }:=\빅컵 _{s^{\alpha }+t^{\alpha }}=1}T_{s,t}.}$

어떤 s을과 함께 시작한;0{\displaystyle\textstyle s>0}, 터>0{\displaystyle\textstyle t>0}sα을 만족시키기+tα=1{\displaystyle\textstyle s^{\alpha}+t^{\alpha}=1}과 어떤(), y)∈ RΔ α{\displaystyle\textstyle \Delta_{\alpha}에 대한 데카르트 표현}쓰기를 하고 있다.+2${\displaystyle \textstyle$ ($x,y)\in \mathb {R} _{+}^{2$ ${\displaystyle {}^{}}$된 지수 $p{\displaystyle }$ ${\displaystyle :=}$ ${\displaystyle 1}$+ ${\displaystyle 1\frac{\mathrm{}}{}}$ α ${\$$displaystyle \mathb{R} ^{2$}}의$$Hölder 부등식 p := 1 + 1 ${\displaystyle \frac{\alpha }{}}$ {\$displaystyp:1+{\frac${1}{\$alpha }}$ 및$$ $q{\displaystyle =}$ ${\displaystyle 1\mathrm{}}$+ $α{1$+\$displaystytype }}}}}}}}}}}}$은 다음을 제공한다.

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+$$t^{\alpha }{\Big )}^{\frac {1}{\alpha$ +$1}=\좌측({\frac {x}{s}+{\frac$ {$y}{t}\오른쪽)^{\frac {\alpha }{\alpha +1$

with equality if and only if ${\displaystyle \textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}}$. In terms of a union of sets the latter inequality reads: the point ${\displaystyle (x,y)\in \mathbb {R} _{+}^{2}}$ belongs to the set ${\displaystyle {\mathrm{\Delta }}_{\alpha }}$${\displaystyle \textstyle \Delta _{\alpha$ $\}\},$$$ ${\displaystyle {s\alpha }^{}}$+ t ${\displaystyle {\alpha }^{}}$= ${\displaystyle 1}$ ${\$}+t^{\alpha $}=1}$의 $일부{\displaystyle {}_{}}$ ${\displaystyle {T,}_{}}$ t$,$ {\$displaystystylease$에 속함$.$

${\displaystyle x^{\frac{\frac {\frac}{\\precent +1}+y^{\frac {\frac}{\frac +1}<1.}$

$더욱이$${\displaystyle {}_{}^{}}$$\Delta {\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {\alpha }_{}}$ ${\$ $\mathb {R} _{+}^{$2$}}$의 경계는 해당$$ 선분할 $계열의$봉투다$.$

${\displaystyle \left\{(x,y)\in \mathb {R} _{+}^{2}:\\\\frac {x}{s}}+{t}=1}}\qquad s^{\alpha }+t^{\alpha }=1}$

(즉, 삼각형의 하이포테누스), 그리고 데카르트 방정식을 가지고 있다.

${\displaystyle x^{\frac {\frac}{\\present +1}+y^{\frac {\frac}{\present +1}=1.}$

특히 $\alpha {\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle \alpha =1}$ 값은 예제 ${\displaystyle 2}$의 포물선 호를$$ 제공하고, $\alpha {\displaystyle }$= 2 ${\displaystyle \alpha =2}($모든 하이포테뉴가 단위 길이 세그먼트라는 의미) 값은 아스트로이드(Astroid)를 제공한다는 점에 유의하십시오.

예 5

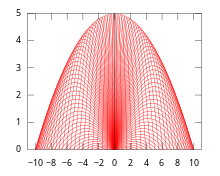
우리는 움직이는 봉투의 다음의 예를 고려한다. 초기 높이 0에서 발사체를 일정한 초기 속도 v를 갖지만 다른 고도 각도 θ로 공중으로 던진다고 가정한다. x를 운동 표면의 수평 축으로 하고 y가 수직 축을 나타내도록 한다. 그 다음 동작은 다음과 같은 차동 동력학적 시스템을 제공한다.

${\dt^{d^{2}y}{dt^{2}}=-g,\;{\frac {d^{2}x}{dt^{2}}=0,}$

네 가지 초기 조건을 만족하는 경우:

${\displaystyle {\frac {dx}{dt}}{\bigg }_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg }_{t=0}=v\sin \theta ,\;x{\bigg }_{t=0}=y{\bigg }_{t=0}=0.}$

여기서 t는 동작 시간을 나타내고, θ은 입면각, g는 중력 가속도를 나타내며, v는 일정한 초기 속도(속도가 아님)이다. 상기 시스템의 해법은 다음과 같은 암묵적인 형태를 취할 수 있다.

${\displaystyle F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}:{2v^{2}\cos ^{2}\theta }}-y=0.}$

봉투 방정식을 찾기 위해 원하는 파생상품을 계산할 수 있다.

${\displaystyle {\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}-{\fract {gx^{2}\tan \tan }{v^{2}\cos }}}}}}}}=0.}$

θ을 제거함으로써 다음과 같은 봉투 방정식에 도달할 수 있다.

${\displaystyle y={\frac {v^{2}}-{\frac {g}{2v^{2}}x^{2}.}$

분명히 결과로 나온 봉투도 오목한 포물선이다.

표면 계열의 외피복

3차원 유클리드 공간의 1-모수 표면 계열은 방정식 집합에 의해 주어진다.

$F(x,y,z,a)=0}$

실제 변수 a에 따라.^[2] 예를 들어, 표면의 곡선을 따라 표면에 접선 평면은 그러한 패밀리를 형성한다.

서로 다른 값 a와 a'에 해당하는 두 표면이 정의된 공통 곡선에서 교차함

${\displaystyle F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\premium }-F(x,y,z,a) \over a^{\premium }-a}=0.}$

a'가 a에 가까워질 때의 한계에서 이 곡선은 a의 표면에 포함된 곡선을 나타내는 경향이 있다.

${\displaystyle F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.}$

이 곡선은 a에 있는 가족의 특징이라고 불린다. a가 변화함에 따라 이러한 특성 곡선의 중심은 표면 계열의 외피라고 불리는 표면을 정의한다.

표면 계열의 외피는 해당 표면의 특성 곡선을 따라 패밀리의 각 표면에 접선된다.

일반화

매끄러운 서브마니폴즈 가족의 봉투에 대한 생각은 자연스럽게 따라온다. 일반적으로 코디멘션 c를 가진 서브매니폴드 계열이 있다면 적어도 그러한 서브매니폴드의 c-모수 계열이 있어야 한다. 예를 들어, 3-공간(c = 2)의 1-모수 곡선군은 일반적으로 봉투가 없다.

적용들

일반 미분 방정식

봉투는 보통의 미분방정식(ODE)의 연구와 연결되며, 특히 ODE의 단수 해법과도 연결된다.^[3] 예를 들어, 포물선 y = x에² 대한 접선 선들의 1-모수 계열을 고려하십시오. 이러한 값은 생성 패밀리 F(t, (x,y) = t² – 2tx + y에 의해 주어진다. 0 수준 집합 F(t₀, (x,y) = 0은 점(t₀,t₀²)의 포물선에 탄젠트 선의 방정식을 제공한다. 등식² t – 2tx + y = 0은 x의 함수로 항상 y에 대해 해결할 수 있으므로 고려하십시오.

${\displaystyle t^{2}-2tx+y(x)=0.\ }$

대체

${\displaystyle t=\왼쪽 사진\frac {dy}{dx}\오른쪽)/2}$

ODE를 주다.

${\displaystyle \left({\frac {dy}{dx}\오른쪽)^{2}\!\!-4x{dy}{dx}}+4y=0.}$

당연히 y = 2tx - t는 모두² 이 ODE에 대한 해결책이다. 그러나, 포물선 y = x인² 이 단일 매개변수 선군의 봉투도 이 ODE에 대한 해결책이다. 또 다른 유명한 예는 클레라우트의 방정식이다.

부분 미분 방정식

봉투는 더 간단한 것으로부터 첫 번째 순서 부분 미분 방정식(PDE)의 더 복잡한 해결책을 만드는 데 사용될 수 있다.^[4] Let F(x,u,Du) = 0 be a first order PDE, where x is a variable with values in an open set Ω ⊂ Rⁿ, u is an unknown real-valued function, Du is the gradient of u, and F is a continuously differentiable function that is regular in Du. Suppose that u(x;a) is an m-parameter family of solutions: that is, for each fixed a ∈ A ⊂ R^m, u(x;a) is a solution of 미분 방정식 미분방정식의 새로운 해법은 첫 번째 해법에 의해 구성될 수 있다(가능한 경우

${\displaystyle D_{a}u(x;a)=0\,}$

x의 함수로 a = φ(x)에 대해 {u(·,a)}_a∈A 함수 계열의 엔벨롭은 다음과 같이 정의된다.

${\displaystyle v(x)=u(x;\varphi(x)),\quad x\in \Oomega ,}$

또한 미분 방정식을 해결한다(계속 다른 함수로 존재한다는 가정).

기하학적으로 v(x)의 그래프는 가족 u(x;a)의 일부 멤버의 그래프와 접하는 모든 곳에 있다. 미분 방정식이 첫 번째 순서이기 때문에 그래프의 접선 평면에 조건을 붙일 뿐이므로, 용액에 닿는 모든 곳의 함수도 해결책이 되어야 한다. 같은 생각이 몽게콘의 적분으로 제1차 순서 방정식의 해법에 기초하고 있다.^[5] 몽게 콘은 접선 공간의 봉투에 의해 잘라낸 (x,u) 변수의 R에ⁿ⁺¹ 있는 원뿔장이다. 각 점에서 첫 번째 순서 PDE까지. PDE의 해결책은 콘 필드의 봉투가 된다.

리만 기하학에서, 리만 다지관의 P 지점을 통과하는 매끄러운 지질학 계열이 봉투를 가지고 있다면, P는 가족의 어떤 지오데틱이 봉투를 교차하는 결합점을 가지고 있다. 변동의 미적분학에서도 더 일반적으로 같은 것이 적용된다: 주어진 점 P를 통해 기능하는 극한가족이 봉투를 가지고 있다면, 극단이 봉투를 교차하는 지점은 P에 대한 결합점이다.

카우스틱스

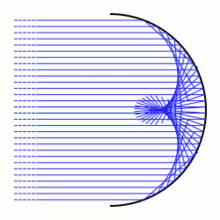
기하학적 광학에서 가성체는 광선 계열의 외피다. 이 그림에는 원의 호가 있다. 광선(파란색으로 표시)은 무한대의 원천에서 나온 것이므로 평행하게 도달한다. 그들이 원형 호를 칠 때 광선은 반사 법칙에 따라 다른 방향으로 흩어진다. 광선이 한 지점에서 호에 닿으면 그 지점에서 호의 접선선에 반사된 것처럼 빛이 반사된다. 반사된 광선은 평면에서 하나의 매개변수 선군을 제공한다. 이 선들의 봉투는 반사적인 가성질이다. 반사 가성비는 일반적으로 매끄러운 점과 평범한 멈춤쇠 점으로 구성된다.

변주성의 미적분학의 관점에서 볼 때, 페르마의 원리(현대의 형태)는 광선이 길이기능의 극치라는 것을 암시한다.

$\displaystyle L[\gamma ]=\int _{a}^{b} \gamma '(t) \,dt}$

완만한 곡선들 사이에서, fixed(a)와 γ(b)가 고정된 엔드포인트가 있는 [a,b]의 γ. 주어진 점 P에 의해 결정되는 가성(이미지에서는 점이 무한에 있다)은 P에 대한 결합점의 집합이다.^[6]

후이겐스의 원리

빛은 광선의 방향과 시작 위치에 따라 서로 다른 비율로 비등방성 이종 매체를 통과할 수 있다. 시간 t 후 주어진 지점 q에서 빛이 이동할 수 있는 지점 세트의 경계는 시간 t 이후의 파동 전선으로 알려져 있으며, 여기서 φ_q(t)로 표시된다. 그것은 빛의 속도로 이동함으로써 q in t 시간에서 도달할 수 있는 점들로 정밀하게 구성된다. Huygens의 원칙은 q φ_q0(t)에 대한 φ_q(s + t) 파전면 φ_q0(s) 계열의 포락선이라고 주장한다. 보다 일반적으로 점 q는₀ 어떤 곡선, 표면 또는 공간의 닫힌 세트로 대체될 수 있다.^[7]

참고 항목

• 지배면
• 가성(수학)

참조

외부 링크

• Weisstein, Eric W. "Envelope". MathWorld.
• MathCurve의 "평면 곡선 패밀리의 개발"