카테노이드

three-dimensional diagram of a catenoid — 고양이과 동물

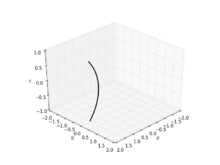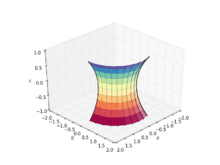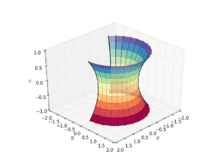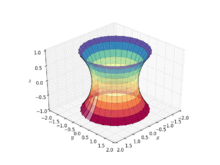
animation of a catenary sweeping out the shape of a catenoid as it rotates about a central point — 캐터리의 회전으로 얻은 캐테노이드

카테노이드(catenoid)는 기하학에서 회전하는 면의 일종으로, 축(^[1]회전면)을 중심으로 카테너리 곡선을 회전시킴으로써 발생합니다.그것은 닫힌 ^[2]공간에 의해 경계될 때 가장 작은 면적을 차지한다는 것을 의미하는 최소 표면입니다.그것은 수학자 레온하르트 오일러에 의해 1744년에 공식적으로 기술되었습니다.

쌍둥이 원형 고리에 부착된 비누 필름은 ^[2]카테노이드의 형태를 취할 것입니다.그들은 동일한 표면 계열의 구성원이기 때문에, 카테노이드는 헬리코이드의 일부로 구부러질 수 있고, 그 반대도 마찬가지입니다.

기하학.

카테노이드는 평면에서 분리되어 발견된 최초의 3차원 유클리드 공간에서 사소하지 않은 최소 표면이었습니다.카테노이드는 ^[2]그 직립선을 중심으로 카테닐을 회전시킴으로써 얻어집니다.그것은 1744년 ^[3]^[4]레온하르트 오일러에 의해 발견되었고 최소임이 증명되었습니다.

이 주제에 대한 초기 연구는 장 바프티스트 ^[5]^[4]^{: 11106}뫼시니에에 의해서도 출판되었습니다.회전의 최소 표면은 평면과 ^[6]카테노이드의 두 가지뿐입니다.

카테노이드는 다음과 같은 파라메트릭 방정식으로 정의할 수 있습니다.

표시({style{aligned}x&=c\cosh{frac{v}{c}\cosu\y&=coshfrac{v}\sinu\z&=v\end{aligned}})

$u\in [-\pi ,\pi )$ 서 u $v\in \mathbb {R}$ $u\in [-\pi ,\pi )$ [ - $u\in [-\pi ,\pi )$ , $u\in [-\pi ,\pi )$ π $]{displaystyle$ u\ $in [-\pi,\pi$ ]}와 $u\in [-\pi ,\pi )$ v ∈ $v\in \mathbb {R}$ {\ $displaystyle$ v $\in \mathbb {R}$ 및 $v\in \mathbb {R}$ ${displaystyle$ c $}$ 는 $c$ 0이 아닌 실수 상수입니다.

원통형 좌표:

{\displaystyle \rho =c\cosh({frac {z}{c})} 표시

$c$ 서 c ${displaystyle$ c $}$ 는 $c$ 실수 상수입니다.

카테노이드의 물리적 모델은 두 개의 원형 고리를 비누 용액에 담그고 원을 천천히 떼어냄으로써 형성될 수 있습니다.

카테노이드는 스트레치 그리드 방법으로 대략적으로 패싯 3D 모델로 정의할 수도 있습니다.

헬리코이드 변환

Continuous animation showing a helicoid deforming into a catenoid and back to a helicoid — 헬리코이드의 카테노이드로의 변형

그들은 동일한 표면 계열의 구성원이기 때문에, 스트레칭 없이 카테노이드를 헬리코이드의 일부로 구부릴 수 있습니다.다시 말해, 변형 패밀리의 모든 구성원이 최소(평균 곡률이 0)가 되도록 헬리코이드의 일부에 대해 카테노이드의 (대부분) 연속적이고 등축적인 변형을 만들 수 있습니다.이러한 변형의 매개 변수화는 시스템에 의해 제공됩니다.

표시(\style{aligned}x(u,v)&=\cos \theta \,\sinh v\,\cos u\y(u,v)&=\cos \theta \,\cos \theta \,\sinh v\,\cos u\z(u,v)&=\cos \v\sin\ta \ta \ta \ta \ta \ta \ta \ta \ta \ta \ta \ta \ta \cos\cos \cos \cos \

$(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$ u $-\pi <\theta \leq \pi$ v ) $-\pi <\theta \leq \pi$ ( - $(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$ , $(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$ π ) × ( - $(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$ $(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$ ) $(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$ {\ $displaystyle$ ( $u,v)\in (-\pi,\pi)\$ times $(-\infty,\infty$ 에 대해 변형 매개변수 - $-\pi <\theta \leq \pi$ < \ $≤$ \ $displaystyle -\pi$ < \ $ta$ \ $pi$ \pi \pi \pi \ta, 여기서, 여기서:

$\theta =\pi$ ◦ = $\theta =\pi$ \ $displaystyle \theta$ = \ $pi }$ 는 $\theta =\pi$ 오른손잡이 헬리코이드에 해당합니다.
$\theta =\pm \pi /2$ ◦ $\theta =\pm \pi /2$ ± $\theta =\pm \pi /2$ / $\theta =\pm \pi /2$ ${\displaystyle \theta$ = \ $pm \pi$ / $2}$ 는 $\theta =\pm \pi /2$ 카테노이드에 해당하며,
$\theta =0$ ◦ $\theta =0$ = $0}$ 은 $\theta =0$ (는) 왼손잡이 헬리코이드에 해당합니다.

레퍼런스

^ Dierkes, Ulrich; Hildebrandt, Stefan; Sauvigny, Friedrich (2010). Minimal Surfaces. Springer Science & Business Media. p. 141. ISBN 9783642116988.
^ ^a ^b ^c Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton & Company. p. 538. ISBN 9780393040029.
^ Helveticae, Euler, Leonhard (1952) [reprint of 1744 edition]. Carathëodory Constantin (ed.). Methodus inveniendi lineas curvas: maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti (in Latin). Springer Science & Business Media. ISBN 3-76431-424-9.{{cite book}}CS1 유지보수: 다중 이름: 작성자 목록(링크)
^ ^a ^b Colding, T. H.; Minicozzi, W. P. (17 July 2006). "Shapes of embedded minimal surfaces". Proceedings of the National Academy of Sciences. 103 (30): 11106–11111. Bibcode:2006PNAS..10311106C. doi:10.1073/pnas.0510379103. PMC 1544050. PMID 16847265.
^ Meusnier, J. B (1881). Mémoire sur la courbure des surfaces [Memory on the curvature of surfaces.] (PDF) (in French). Bruxelles: F. Hayez, Imprimeur De L'Acdemie Royale De Belgique. pp. 477–510. ISBN 9781147341744.
^ "Catenoid". Wolfram MathWorld. Retrieved 15 January 2017.

진일보한 내용

Krivoshapko, Sergey; Ivanov, V. N. (2015). "Minimal Surfaces". Encyclopedia of Analytical Surfaces. Springer. ISBN 9783319117737.

외부 링크

"Catenoid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Catenoid - WebGL 모델
카네기 멜론 대학의 카테노이드를 설명하는 오일러의 글
카테노이드의 표면적 계산
최소 회전 표면

[1] Dierkes, Ulrich; Hildebrandt, Stefan; Sauvigny, Friedrich (2010). Minimal Surfaces. Springer Science & Business Media. p. 141. ISBN 9783642116988.

[Gullberg-2] Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton & Company. p. 538. ISBN 9780393040029.

[3] Helveticae, Euler, Leonhard (1952) [reprint of 1744 edition]. Carathëodory Constantin (ed.). Methodus inveniendi lineas curvas: maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti (in Latin). Springer Science & Business Media. ISBN 3-76431-424-9.{{cite book}}CS1 유지보수: 다중 이름: 작성자 목록(링크)

[Colding06-4] Colding, T. H.; Minicozzi, W. P. (17 July 2006). "Shapes of embedded minimal surfaces". Proceedings of the National Academy of Sciences. 103 (30): 11106–11111. Bibcode:2006PNAS..10311106C. doi:10.1073/pnas.0510379103. PMC 1544050. PMID 16847265.

[salvert-5] Meusnier, J. B (1881). Mémoire sur la courbure des surfaces [Memory on the curvature of surfaces.] (PDF) (in French). Bruxelles: F. Hayez, Imprimeur De L'Acdemie Royale De Belgique. pp. 477–510. ISBN 9781147341744.

[6] "Catenoid". Wolfram MathWorld. Retrieved 15 January 2017.

[1]

[2]

[3]

[4]

[5]

[6]

Search