This is a good article. Click here for more information.

이중 그래프

Dual graph
빨간색 그래프는 파란색 그래프의 이중 그래프이며, 그 반대도 마찬가지다.

그래프 이론의 수학적 학문에서 평면 그래프 G의 이중 그래프는 G의 각 면에 대해 꼭지점이 있는 그래프다.이중 그래프는 엣지에 의해 서로 분리되어 있는 G의 각 면 쌍에 대한 엣지를 가지고 있으며, 엣지 양쪽에 동일한 얼굴이 나타날 때 셀프 루프(self-loop)를 가지고 있다.따라서 G의 각 에지 e에는 해당하는 이중 에지가 있으며, 끝점은 e의 양쪽에 있는 면에 해당하는 이중 정점이다.이중의 정의는 그래프 G의 내장 선택에 따라 달라지기 때문에 평면 그래프(내장될 수 있지만 내장을 아직 알 수 없는 그래프)가 아니라 평면 그래프(이미 평면에 내장되어 있는 그래프)의 속성이다.평면 그래프의 경우 일반적으로 그래프의 평면 내장 선택에 따라 여러 개의 이중 그래프가 있을 수 있다.

역사적으로, 그래프 이중성의 첫 번째 형태는 플라토닉 고형물을 이중 다면체 쌍으로 연결한 것이었다.그래프 이중성은 이중 다면체 및 이중 테셀레이션의 기하학적 개념을 위상학적으로 일반화한 것으로, 차례로 이중 매트로이드 개념에 의해 대수학적으로 일반화된다.평면 그래프 이중성의 변화에는 지시된 그래프의 이중성 버전과 평면 2차원 표면에 내장된 그래프의 이중성이 포함된다.그러나 이러한 이중 그래프의 개념은 다른 개념, 즉 그래프의 에지 대 버텍스 듀얼 또는 선 그래프와 혼동해서는 안 된다.

이중 그래프가 되는 속성이 대칭이기 때문에 이중이라는 용어를 사용하는데, 이는 H가 연결된 그래프 G의 이중이라면 G는 H의 이중이라는 뜻이다.그래프 G의 이중성을 논의할 때 그래프 G 자체를 "기본 그래프"라고 할 수 있다.다른 많은 그래프 속성 및 구조물은 이중의 다른 자연적 특성과 구조로 변환될 수 있다.예를 들어, 사이클은 절단에 이중이고 스패닝 트리는 스패닝 트리의 보완에 이중이며, 단순 그래프(평행 에지 또는 자체 루프 제외)는 3 엣지 연결 그래프에 이중이다.

그래프 이중성은 미로와 배수 분지의 구조를 설명하는 데 도움이 될 수 있다.컴퓨터 비전, 컴퓨터 기하학, 메쉬 생성, 집적회로 설계에도 듀얼 그래프가 적용됐다.

예

사이클 및 쌍극점

쌍극자 그래프
사이클 그래프

사이클 그래프가 내장된 독특한 평면형 구조는 조던 곡선 정리에 의해 평면을 사이클 내외부의 두 영역으로만 나눈다.단, n 사이클에서는 이 두 영역이 서로 다른 가장자리 n개로 분리된다.따라서 n 사이클의 이중 그래프는 두 개의 꼭지점(지역까지 이중)이 있는 다중 글자로, n개의 이중 가장자리로 서로 연결되어 있다.그런 그래프를 쌍극 그래프라고 한다.반대로 n-엣지 쌍극자 그래프의 이중은 n 사이클이다.[1]

이중 다면체

주요 기사:이중 다면체
정육면체와 일반 옥타헤드론은 서로에 대한 이중 그래프다.

슈타인리츠의 정리에 따르면 모든 다면 그래프(삼차원 볼록 다면체의 정점과 모서리로 형성된 그래프)는 평면과 3-Vertex 연결되어야 하며, 모든 3-Vertex 연결 평면 그래프는 이런 방식으로 볼록 다면체에서 나온다.모든 3차원 볼록한 다면체는 이중 다면체를 가지고 있고, 이중 다면체는 원래 다면체의 모든 면에 정점을 가지고 있으며, 해당 두 면이 모서리를 공유할 때마다 두 개의 이중 정점이 인접해 있다.두 개의 다면체가 이중일 때마다, 그들의 그래프 또한 이중이다.예를 들어 플라토닉 고형물은 이중 쌍으로, 8면체는 정육면체에, 도면체는 고면체에, 사면체는 그 자체로 이중으로 나온다.[2]다면체 이중성은 고차원 다면체의 이중성으로도 확장될 수 있지만,[3] 이 기하학적 이중성의 확장은 그래프-이중성과의 명확한 연결을 가지고 있지 않다.

자체 이중 그래프

자체 이중 그래프.

평면 그래프는 이중 그래프와 이형성이면 자가이중이라고 한다.휠 그래프는 자기 이중 다면체( 피라미드)에서 나오는 자기 이중 그래프의 무한 패밀리를 제공한다.[4][5]단, 다면체(多面體)가 아닌 자기 이중 그래프(self-dual graph)도 존재하는데, 예를 들면 다면체(多面體)가 아니다.Servatius & Christopher(1992)는 주어진 평면 그래프를 포함하는 자체 이중 그래프를 구성하는 데 사용할 수 있는 접착과 폭발의 두 가지 작동을 설명한다. 예를 들어, 표시된 자체 이중 그래프는 이중으로 4면체의 접착으로 구성할 수 있다.[5]

정점이 n인 모든 자체 이중 그래프에는 정확히 2n - 2 에지가 있다는 오일러의 공식에 따른 것이다.[6]모든 간단한 자기 이중 평면 그래프는 3도의 정점 4개를 포함하며, 모든 자기 이중 내장에는 최소한 4개의 삼각형 면이 있다.[7]

특성.

그래프 이론의 많은 자연적이고 중요한 개념들은 이중 그래프에서 똑같이 자연스럽지만 다른 개념들과 일치한다.연결된 평면 그래프의 이중은 원시 그래프와 이형이기 때문에 이들 쌍은 양방향으로 이루어지는데,[8] 평면 그래프의 개념 X가 이중 그래프의 개념 Y에 해당하면 평면 그래프의 개념 Y는 이중의 개념 X에 해당한다.

단순 그래프 대 다중 그래프

단순 그래프의 이중은 단순할 필요가 없다. 즉, 쌍극자 다중 그래프가 그래프를 순환하기 위해 이중화된 예에서 이미 분명히 나타났듯이, 자체 루프(두 끝점이 동일한 두 정점에 있는 가장자리) 또는 동일한 두 꼭지점을 연결하는 다중 가장자리가 있을 수 있다.아래에서 설명하는 컷 사이클 이중성의 특별한 경우로서 평면 그래프 G의 다리는 듀얼 그래프의 자체 루프와 일대일 일치한다.[9]같은 이유로 이중 다중 그래프의 평행 가장자리 쌍(길이-2 사이클)은 원시 그래프의 2-엣지 컷셋(삭제가 그래프를 분리하는 가장자리 쌍)에 해당한다.따라서 평면 그래프는 이중의 1 엣지 또는 2 엣지 컷 세트가 없는 경우에만, 즉 3 엣지 연결인 경우에만 간단하다.듀얼이 단순한 단순 평면 그래프는 정확히 3개의 엣지로 연결된 단순 평면 그래프다.[10]이 그래프 클래스는 3Vx로 연결된 단순 평면 그래프를 포함하지만 동일하지는 않다.예를 들어, 자기 이중 그래프를 보여주는 그림은 3-엣지 연결이지만(따라서 이중은 단순하다) 3-벡스 연결은 아니다.

유니크함

두 개의 빨간색 그래프는 파란 그래프에 이중이지만 이형성이 없다.

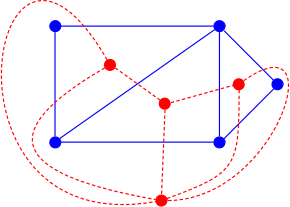
이중 그래프는 특정 임베딩에 따라 달라지기 때문에 동일한 평면 그래프가 비이등형 이중 그래프를 가질 수 있다는 점에서 평면 그래프의 이중 그래프는 고유하지 않다.[11]사진에서, 파란색 그래프는 이형이지만 그들의 이중 적색 그래프는 그렇지 않다.상부 적색 이중의 정점은 6도인 반면(파란색 그래프의 바깥 면에 해당) 하부 적색 그래프에서 모든도는 6도 미만이다.

Hassler Whitney는 그래프가 3개 연결되면 내장, 즉 이중 그래프가 독특하다는 것을 보여주었다.[12]슈타인리츠의 정리로는, 이 그래프들은 정확히 다면 그래프, 즉 볼록 다면체의 그래프들이다.평면 그래프는 이중 그래프가 3-Vertex 연결되었을 경우에만 3-Vertex 연결된다.보다 일반적으로 평면 그래프는 고유한 내장을 가지며, 따라서 3Vx로 연결된 평면 그래프(가장자리 일부를 경로별로 교체하여 3Vx로 연결된 평면 그래프)의 하위분할인 경우에만 고유한 이중 그래프를 가진다.완전한 양분 그래프 K와2,4 같이 3-Vertex로 연결되지 않은 일부 평면 그래프의 경우 임베딩은 고유하지 않지만 모든 임베딩은 이형성이다.이 경우, 그에 상응하여 모든 이중 그래프는 이형성이다.

서로 다른 임베딩이 다른 이중 그래프로 이어질 수 있기 때문에 한 그래프가 다른 그래프의 이중인지(이미 임베딩 사실을 알지 못한 채) 테스트하는 것은 비종교 알고리즘 문제다.이코넥트 그래프의 경우 그래프의 SPQR 트리를 사용하여 공유상호 이중화 관계에 대한 표준적 형태를 구성하면 다항식 시간에 해결할 수 있다.예를 들어, 그림의 두 빨간색 그래프는 이 관계에 따라 동일하다.단, 쌍방향으로 연결되지 않은 평면 그래프의 경우 이 관계는 동등성 관계가 아니며 상호 이중성을 검정하는 문제는 NP-완전성이다.[13]

절삭 및 주기

임의로 연결된 그래프의 컷셋은 정점의 파티션에서 정의한 에지의 서브셋으로, 파티션의 양쪽에 끝점이 하나 있을 때 서브셋에 에지를 포함시켜 두 개의 서브셋으로 정의한 서브셋이다.절단 세트의 가장자리를 제거하면 그래프가 적어도 두 개의 연결된 구성요소로 분할되어야 한다.최소 컷셋(본드라고도 함)은 컷셋의 모든 적절한 서브셋이 그 자체가 컷이 아니라는 특성을 가진 컷셋이다.연결된 그래프의 최소 컷셋은 그래프를 정확히 두 개의 구성요소로 분리해야 하며, 각 구성요소에 하나의 끝점이 있는 가장자리 집합으로 구성된다.[14]단순 사이클은 사이클의 각 정점이 사이클의 정확히 두 가장자리에 충돌하는 연결된 서브그래프다.[15]

연결된 평면 그래프 G에서 G의 모든 단순 주기는 G의 이중에서 최소 컷셋에 해당하며, 그 반대의 경우도 마찬가지다.[16]이것은 요르단 곡선 정리의 한 형태로 볼 수 있는데, 각 단순 사이클은 사이클 내부의 G 면과 사이클 외면의 면으로 구분되며, 사이클 에지의 이중은 정확히 실내에서 외부로 교차하는 가장자리들이다.[17]평면 그래프의 둘레(가장 작은 주기의 크기)는 이중 그래프의 가장자리 연결(가장 작은 컷셋의 크기)과 동일하다.[18]

이 이중성은 개별 컷셋과 사이클에서 그것들로부터 정의된 벡터 공간까지 확장된다.그래프의 사이클 공간은 각 꼭지점에서 짝수도를 갖는 모든 서브그래프의 패밀리로 정의된다. 이는 2요소 유한장을 통한 벡터 공간으로 볼 수 있으며, 두 에지의 대칭적 차이가 벡터 공간에서 벡터 추가 연산의 역할을 한다.마찬가지로, 그래프의 절단 공간은 모든 절단 세트의 패밀리로 정의되며 벡터 추가는 동일한 방식으로 정의된다.그러면 평면 그래프의 주기 공간과 이중 그래프의 절삭 공간은 벡터 공간으로서 이형성이 된다.[19]따라서 평면 그래프의 순위(절단 공간의 치수)는 그 이중(주기 공간의 치수)의 사이클로토믹 숫자와 같으며, 그 반대의 경우도 마찬가지다.[11]그래프의 사이클 기준은 사이클 공간의 기초를 이루는 단순한 사이클 집합이다(모든 이등도 서브그래프는 이러한 사이클 중 일부의 대칭적 차이로 정확히 한 가지 방법으로 형성될 수 있다).에지 가중 평면 그래프(두 사이클이 동일한 가중치를 가지지 않을 정도로 충분히 일반적인 가중치를 가진 경우)의 경우, 그래프의 최소 가중 주기 기준은 이중 그래프의 고모리-후 트리에 이중으로 적용되며, 내포된 자르기 집합은 그래프에서 각 정점 쌍을 구분하는 최소 절단을 포함한다.최소 중량 사이클 기준의 각 사이클에는 고모리-후 트리의 절단 중 하나의 가장자리에 이중인 일련의 가장자리가 있다.주기 가중치를 묶을 수 있는 경우 최소 가중치 주기가 고유하지 않을 수 있지만, 이 경우 이중 그래프의 고모리-후 트리가 그래프의 최소 가중치 기준 중 하나에 해당하는 것은 사실이다.[19]

지시된 평면 그래프에서 단순 지시 주기는 지시된 절단(정점들을 두 개의 부분 집합으로 구성하여 모든 가장자리가 한 방향으로, 한 부분 집합에서 다른 방향으로 이동)에 이중적이다.강한 방향의 평면 그래프(기본적인 비방향 그래프가 연결되어 있고 모든 에지가 사이클에 속하는 그래프)는 에지가 사이클에 속하지 않는 방향의 악순환 그래프에 이중적이다.이것을 다른 방법으로 표현하면, 연결된 평면 그래프의 강한 방향(그래프의 가장자리에 강하게 연결된 방향의 할당)은 악순환 방향(직접된 악순환 그래프를 생성하는 방향의 할당)에 이중적이다.[20]

스패닝 트리

미로 벽과 벽 사이의 자유 공간이 두 개의 디지트로 된 나무를 이루는 단순한 미로

스패닝 트리는 그래프의 모든 정점과 함께 연결되고 반복적인 하위 그래프를 형성하는 가장자리 집합으로 정의될 수 있다.단, 컷 사이클 이중성에 의해 평면 그래프 G의 에지 세트 S가 Acyclic(주기가 없는 경우), S에 대한 듀얼 에지 세트에는 절단이 없으며, 여기에서 듀얼 에지의 보완 세트(S에 없는 에지의 듀얼)가 연결된 서브그래프를 형성한다.대칭적으로, S가 연결된 경우, S의 보완에 이중으로 된 가장자리가 Acyclic 서브그래프를 형성한다.따라서 S가 두 가지 속성(연결된 속성 및 반복적인 속성)을 모두 가질 경우, 이중 그래프에 있는 상호보완적인 집합에서도 마찬가지다.즉, G의 각 스패닝 트리는 듀얼 그래프의 스패닝 트리와 상호 보완적이다.따라서 평면 그래프의 가장자리와 그 이중의 가장자리는 함께 원시 그래프와 이중 그래프에 있는 두 개의 스패닝 트리로 분할될 수 있으며, 이 트리는 그래프의 모든 정점과 면으로 확장되지만 서로 교차하지 않는다.특히 G의 최소 스패닝 트리는 듀얼 그래프의 최대 스패닝 트리와 보완된다.[21]단, 이것은 최단 경로 트리에는 적용되지 않는다. 그래프의 스패닝 트리 쌍과 듀얼 그래프의 보완적 스패닝 트리 쌍에 대해, 두 트리 중 적어도 하나의 거리가 그래프에 있는 거리보다 현저히 길다는 평면 그래프가 존재한다.[22]

이러한 종류의 분해의 예는 입구가 한 개이고 벽의 분리된 구성요소가 없는 단순한 미로의 일부 유형에서 볼 수 있다.이 경우 미로 벽과 벽 사이의 공간은 모두 수학적 나무의 형태를 취한다.만일 미로의 자유공간이 단순한 세포(그리드 사각형 등)로 분할된다면, 이 세포체계는 벽의 트리 구조가 그래프의 스패닝 트리를 형성하고 자유 공간의 트리 구조가 이중 그래프의 스패닝 트리를 형성하는 평면 그래프를 내장한 것으로 볼 수 있다.[23]배수 유역 내 하천과 강의 나무 모양 패턴과 하천을 분리하는 능선 이중 나무 모양 패턴에서도 유사한 쌍의 간지화 나무를 볼 수 있다.[24]

가장자리와 그 이중의 이 분할은 V 정점, E 가장자리, F면이 있는 평면 그래프의 경우 오일러의 공식 V - E + F = 2를 간단하게 증명한다.모든 스패닝 트리와 그 보완적인 이중 스패닝 트리는 가장자리를 각각 V - 1과 F - 1 에지의 두 하위 집합으로 분할하고, 두 하위 집합의 크기를 추가하면 방정식이 제공된다.

E = (V − 1) + (F − 1)

오일러의 공식을 만들기 위해 재배열될 수 있다.던컨 소머빌에 따르면 오일러의 공식에 대한 이 증거는 K. G. C. 폰 스토트의 기하학적 디어 라지(Nürnberg, 1847년) 때문이다.[25]

비 평면 표면에서 스패닝 트리를 보완하는 이중 가장자리 세트는 이중 스패닝 트리가 아니다.대신 이 에지 집합은 그래프가 내장된 표면의 속성에 의해 숫자가 결정되는 작은 여분의 에지 집합을 가진 이중 스패닝 트리의 결합이다.여분의 가장자리는 스패닝 트리의 경로와 결합하여 표면의 기본 그룹을 생성하는데 사용될 수 있다.[26]

추가 속성

모든 평면 그래프에 유효한 정점과 면을 포함하는 계산식은 평면 이중성에 의해 정점과 면의 역할이 바뀐 동등한 공식으로 변환될 수 있다.오일러의 자기이중식(self-dual)이 그 한 예다.Harary가 제공한 또 다른 것은 악수하는 보조정리기를 포함하는데, 그에 따라 어떤 그래프의 정점도의 합은 가장자리 수의 두 배와 같다.이중 형태에서, 이 보조정리자는 평면 그래프에서, 그래프의 면의 숫자의 합이 가장자리 수의 두 배와 같다고 말한다.[27]

평면 그래프의 내측 그래프는 이중의 내측 그래프와 이형성이다.두 평면 그래프는 서로 이중인 경우에만 이형 내분 그래프를 가질 수 있다.[28]

정점이 4개 이상인 평면 그래프는 이중 그래프가 3-Vertex 연결 및 3-정규 그래프인 경우에만 최대값(평면성을 보존하면서 더 이상 에지를 추가할 수 없음)이다.[29]

연결된 평면 그래프는 이중 그래프가 초당적인 경우에만 오일러(모든 꼭지점에서 짝수 도수를 가진다)이다.[30]평면 그래프 G의 해밀턴 사이클은 유도 서브그래프가 모두 나무인 두 하위 집합(주기의 내부와 외부)으로 이중 그래프의 정점을 분할하는 것에 해당한다.특히 바넷의 입방체 쌍방 다면 그래프의 해밀턴시티에 대한 추측은 모든 오일리언 최대 평면 그래프를 두 개의 유도 나무로 분할할 수 있다는 추론과 맞먹는다.[31]

평면 그래프 G에 Tutte 다항식G T(x,y)가 있는 경우, 이중 그래프의 Tutte 다항식은 x와 y를 스와핑하여 얻는다.이러한 이유로, Tutte 다항식의 어떤 특정 값이 G의 특정 구조 유형에 대한 정보를 제공하는 경우, 인수를 Tutte 다항식으로 바꾸면 이중 구조에 대한 해당 정보가 제공된다.예를 들어, 강한 방향의 수는G T(0,2)이고, 반복 방향의 수는G T(2,0)이다.[32]브리지가 없는 평면 그래프의 경우, k 색상의 그래프 색상은 이중 그래프에서 0이 아닌 흐름 모듈로 k에 해당한다.예를 들어, 4가지 색상 정리(모든 평면 그래프에 대해 4-색상이 존재함)는 모든 브리지 없는 평면 그래프의 이중에는 0이 없는 4-흐름이 있다고 기술하는 것과 동등하게 표현될 수 있다.k-색상의 수는 투테 다항식 값 T(1G - k,0)에 의해 계수되고(쉽게 계산된 요인까지), 한 달에 한 번 0이 아닌 k-흐름의 수는 TG(0,1 - k)에 의해 계수된다.[33]

st-planar graph는 그 그래프의 양극 방향과 함께 연결된 평면 그래프로, 하나의 소스 및 단일 싱크와 반복되도록 하는 방향이며, 두 그래프 모두 서로 같은 면에 있어야 한다.이러한 그래프는 싱크대부터 소스까지 외부 표면을 통해 하나의 가장자리를 더 추가함으로써 강하게 연결된 그래프로 만들어질 수 있다.이 증강 평면 그래프의 이중은 그 자체로 또 다른 표준 평면 그래프의 확대다.[34]

변형

지시 그래프

방향 평면 그래프에서, 이중 그래프는 각 이중 가장자리의 방향을 해당 원시 가장자리에서 시계 방향으로 90° 돌림으로써 지시될 수도 있다.[34]엄밀히 말하면, 이 구성은 G 그래프에서 시작해서 이중으로 두 번 찍으면 G 그 자체로 되돌아가지 않고 G의 전치 그래프인 G의 전치 그래프에 이형성 그래프를 구성하기 때문에 지시된 평면 그래프의 이중성이 아니다.듀얼을 네 번 찍으면 원래 그래프로 돌아온다.

약한 이중

평면 그래프의 약한 이중은 정점이 원시 그래프의 경계면에 해당하는 이중 그래프의 하위 그래프다.평면 그래프는 약한 이중성이 숲인 경우에만 외부 평면이다.어떤 평면 그래프 G의 경우, G의+ 무한 면에 하나의 새로운 정점 v를 추가하고, 외부 면의 각 정점에 v를 연결함으로써 형성된 평면 다중 글자가 되도록 한다(여러 번, 외부 면의 경계에 정점이 여러 번 나타나면), G는 G의+ (평면) 이중의 약한 이중이다.[35]

무한 그래프 및 테셀레이션

이중성의 개념은 유한 그래프에 적용되는 것처럼 평면에 포함된 무한 그래프에도 적용된다.그러나 그래프에서 열린 영역의 일부가 아닌 평면의 점이나 그래프의 가장자리 또는 꼭지점의 일부와 같은 위상학적 복잡성을 방지하기 위해 주의가 필요하다.모든 면이 그래프의 사이클로 둘러싸인 경계 영역일 때 무한 평면 그래프 내장도 면의 테셀레이션으로 볼 수 있으며, 내부(임베딩의 면)이 분리된 밀폐 디스크(테셀레이션의 타일)에 의한 평면 커버(테셀레이션의 타일)로 볼 수 있다.평면 이중성은 각 기와의 중심에 꼭지점을 두고 인접한 기와의 중심을 연결함으로써 형성된 테셀레이션인 이중 테셀레이션의 개념을 낳는다.[36]

유한 점 집합(검은 점)의 보로노이 다이어그램(빨간색) 및 딜라우나이 삼각측량(검은색)

이중 테셀레이션의 개념은 평면의 분할에도 적용되어 매우 많은 지역으로 갈 수 있다.이것은 이 경우 평면 그래프 이중성과 밀접하게 관련되어 있지만 그다지 동일하지는 않다.예를 들어, 유한한 점 부위의 보로노이 도표는 한 부지가 다른 어떤 부위보다 가까운 폴리곤으로 평면을 분할한 것이다.입력의 볼록한 선체에 있는 부위는 무한대의 보로노이 폴리곤을 발생시키는데, 그 중 두 면은 유한 선분할이 아닌 무한의 광선이다.이 다이어그램의 이중은 입력의 Delaunay 삼각측량이며, 두 사이트를 포함하고 다른 사이트가 없는 원이 존재할 때마다 두 사이트를 가장자리로 연결하는 평면 그래프다.입력의 볼록한 선체의 가장자리도 델라오나이 삼각측량의 가장자리지만, 보로노이 다이어그램의 선분할보다는 광선에 해당한다.보로노이 다이어그램 및 들로네 triangulations 사이에 이 이중성 유한 그래프 사이의 이중성에에서 다음 두가지 방법 중 하나:무한대의 보로노이 다이어그램에, 모든 rays,[37]의 다른 끝점이나 들로네의 약한 이중의 보로노이 다이어그램의 한정적 부분을 다룸으로써 역할을 하는 인공 꼭지점을 추가함으로써 바뀔 수 있다.tr이앙의비록 보로노이 다이어그램과 델라오나이 삼각측량은 이중이지만, 이들의 평면 내 내장에는 이중 가장자리 쌍의 교차점을 넘어 추가 교차점이 있을 수 있다.딜라우나이 삼각형의 각 꼭지점은 보로노이 다이어그램의 해당 면 안에 위치한다.보로노이 다이어그램의 각 꼭지점은 델라오나이 삼각측량에서 해당하는 삼각형의 원곡점에 위치하지만, 이 점은 삼각형 밖에 있을 수 있다.

비플래너 임베딩

K는7 토러스에서 히우드 그래프와 이중이다.
K는6 투영 평면에서 Petersen 그래프와 이중이다.

이중성의 개념은 평면 이외의 2차원 다지관에 임베딩하는 그래프로 확장될 수 있다.정의는 동일하다: 다지관의 그래프 보완의 연결된 각 구성요소에 대해 이중 정점이 있고, 가장자리 양쪽에 있는 두 개의 이중 정점을 연결하는 각 그래프 에지에 대해 이중 정점이 있다.이 개념의 대부분의 적용에서, 각 면이 위상학적 디스크라는 속성과 함께 임베딩하는 것으로 제한된다. 이 제약조건은 그래프가 연결되는 평면 그래프의 요건을 일반화한다.이 제약조건으로, 어떤 표면 내장 그래프의 이중은 동일한 표면에 자연적으로 내장되어 있어, 이중의 이중은 원래 그래프에 이형성적이며 이형적으로 내장되어 있다.예를 들어, 전체 그래프 K는7 토로이드 그래프인데, 평면 그래프는 아니지만 토러스 안에 삽입될 수 있으며, 내장 각 면은 삼각형이다.이 임베딩은 히우드 그래프를 이중 그래프로 가지고 있다.[38]

같은 개념이 방향성이 없는 표면에도 똑같이 잘 작용한다.예를 들어 K는6 10개의 삼각면을 헤미-icosaheadron으로 하여 투영면에 삽입할 수 있으며, 이중은 헤미-도-케드론(hemi-deadheadron)으로 내장된 피터슨 그래프가 있다.[39]

평면 그래프조차 평면 이중과 다른 이중에서 파생된 이중으로 비 평면 임베딩이 있을 수 있다.예를 들어, 큐브의 네 개의 페트리 폴리곤(입방체의 정점 두 개를 제거하여 형성된 헥사곤)은 토러스 안에 큐브를 내장한 육각형의 면을 형성한다.이 임베딩의 이중 그래프에는 두 개의 가장자리가 있는 완전한 그래프 K를4 형성하는 네 개의 정점이 있다.이 이중 그래프의 내포된 토러스에서, 6개의 가장자리는 그 정점 주위의 주기적인 순서로 각 정점에 입사하며, 다른 3개의 정점을 통해 두 번 순환한다.평면의 상황과 대조적으로, 큐브와 그 이중의 이 내장형은 독특하지 않다; 큐브 그래프에는 다른 이중의 여러 다른 토러스 임베딩이 있다.[38]

평면 그래프의 원시 그래프와 이중 그래프 속성 사이의 상당수는 비 평면 이중으로 일반화하지 못하거나 일반화에 추가적인 주의가 필요하다.

표면 임베딩 그래프에 대한 또 다른 작업은 임베딩의 페트리 폴리곤을 새로운 임베딩의 면으로 사용하는 페트리 듀얼이다.일반적인 이중 그래프와 달리 정점이 원래 그래프와 같지만 일반적으로는 다른 표면에 놓여 있다.[40]표면 이중성과 페트리 이중성은 윌슨 6개 작업 중 2개 작업이며, 함께 이러한 작업 그룹을 생성한다.[41]

매트로이드와 대수 이중

연결된 그래프 G의 대수적 이중은 G와 G가★ 동일한 가장자리 집합을 가지며, G의 어떤 사이클도★ G의 절단이며, G의 어떤 컷도 G의★ 주기인 그래프 G이다★. 모든 평면 그래프에는 일반적으로 고유하지 않은 대수적 이중성이 있다(평면 내장에 의해 정의된 모든 이중은 가능하다).Hasler Whitney가 Whitney의 평면성 기준에서 정리한 바와 같이, 그 반대는 실제로 사실이다.[42]

연결된 그래프 G는 대수적 이중성이 있는 경우에만 평면형이다.

같은 사실을 모태론에서도 표현할 수 있다.M이 그래프 G의 그래픽 매트로이드인 경우 G의★ 그래픽 매트로드가 M의 이중 매트로이드인 경우에만 그래프 G는★ G의 대수적 이중이다.휘트니의 평면성 기준은 그래픽 매트로이드 M의 이중 매트로이드 그 자체가 M의 기초 그래프 G가 평면인 경우에만 그래픽 매트로이드라고 말하는 것으로 다시 해석될 수 있다.G가 평면인 경우, 이중 매트로드는 G의 이중 그래프의 그래픽 매트로이드다.특히 G의 모든 평면 임베딩에 대해 모든 이중 그래프에는 이형성 그래픽 매트로이드가 있다.[43]

비 평면 표면 임베딩의 경우 평면 이중과 달리 이중 그래프는 일반적으로 원시 그래프의 대수적 이중 그래프가 아니다.그리고 비 평면 그래프 G의 경우 G의 그래픽 매트로이드의 이중 매트로이드 자체가 그래픽 매트로이드 자체가 아니다.그러나 여전히 회로가 G의 절단에 해당하는 매트로이드로, 이런 의미에서 G의 일반화된 대수학적 이중으로 생각할 수 있다.[44]

오일러 그래프와 초당적 평면 그래프 사이의 이중성은 2진법 매트로이드(평면 그래프에서 파생된 그래픽 매트로이드 포함): 2진법 매트로이드는 이중 매트로이드인 경우에만 오일러이다.[30]둘레와 가장자리 연결의 두 가지 이중 개념은 매트로이드 둘레에 의해 매트로이드 이론으로 통일된다: 평면 그래프의 그래픽 매트로이드 둘레는 그래프의 둘레와 동일하며, 이중 매트로이드(듀얼 그래프의 그래픽 매트로이드)의 둘레는 그래프의 가장자리 연결이다.[18]

적용들

그래프 이론에서의 그것의 사용과 함께 평면 그래프의 이중성은 수학적 및 계산적 연구의 몇 가지 다른 영역에 응용이 있다.

지리 정보 시스템에서 흐름 네트워크(하천과 강의 시스템에서 물이 어떻게 흐르는지 보여주는 네트워크 등)는 배수 구분을 기술하는 셀룰러 네트워크에 이중적이다.이러한 이중성은 적절한 눈금의 격자 그래프의 스패닝 트리로서 플로우 네트워크를 모델링하고, 이중 격자 그래프에서 리지선의 보완 스패닝 트리로서 배수 분열을 모델링함으로써 설명할 수 있다.[45]

컴퓨터 비전에서는 디지털 이미지가 작은 사각 픽셀로 분할되는데, 각각의 화소는 고유의 색을 가지고 있다.이 분할된 정사각형의 듀얼 그래프는 픽셀 당 정점과 가장자리를 공유하는 픽셀 쌍 사이의 가장자리를 가지고 있다. 이는 유사한 색상의 연결된 영역으로 픽셀을 클러스터링하는 것을 포함한 어플리케이션에 유용하다.[46]

계산 기하학에서 보로노이 다이어그램과 델로나이 삼각측량 사이의 이중성은 보로노이 다이어그램의 구성을 위한 알고리즘을 즉시 델로나이 삼각측량 알고리즘으로 변환할 수 있다는 것을 의미하며, 그 반대의 경우도 마찬가지다.[47]유한요소 메시 생성에도 동일한 이중성을 사용할 수 있다.로이드 알고리즘은 표면의 점 집합을 보다 균일한 간격으로 이동시키기 위한 보로노이 도표에 기초한 방법으로 이중 들라우나이 삼각측정에 의해 기술된 유한요소 메쉬를 매끄럽게 하는 방법으로 일반적으로 사용된다.이 방법은 삼각형의 크기를 균일하게 하고 모양을 만들어 망사를 개선한다.[48]

CMOS 회로의 합성에서는 합성할 함수가 부울대수에서 공식으로 표현된다.그런 다음 이 공식을 병렬 다중 글자로 두 열로 변환한다.이러한 그래프는 그래프 가장자리가 트랜지스터를 나타내는 회로 다이어그램으로 해석될 수 있으며, 함수에 대한 입력에 의해 게이트된다.한 회로는 함수 자체를 계산하고, 다른 회로는 그 보완물을 계산한다.두 회로 중 하나는 공식의 접속사 및 분리를 각각 그래프의 직렬 및 병렬 구성으로 변환하여 도출한다.다른 회로는 이 구성을 역전시켜 공식의 접속사 및 분리를 그래프의 병렬 및 직렬 구성으로 변환한다.[49]이 두 회로는 각 회로의 입력을 출력물에 연결하는 추가 에지에 의해 증강된 평면 이중 그래프다.[50]

역사

볼록 폴리에드라의 이중성은 요하네스 케플러에 의해 1619년 저서 하모니스 먼디에서 인정받았다.[51]다면체의 맥락에서 벗어난 인식 가능한 평면적 이중 그래프는 1725년 피에르 바리뇽의 사후에 출판된 작품인 Nouvelle Méchanique ou Statique에 일찍 나타났다.이것은 레온하르트 오일러의 1736년 쾨니히스베르크의 일곱 다리 연구 이전에도 있었는데, 이것은 그래프 이론의 첫 번째 작품으로 받아들여진다.바리뇽은 스트럿의 힘에 비례하는 가장자리 길이를 가진 그래프를 스트럿에 이중으로 그려 스트럿의 정적 시스템에 대한 힘을 분석했다. 이 이중 그래프는 크레모나 다이어그램의 일종이다.[52]4색 정리( theorem色 정리)와 관련하여, 지도(비행기의 영역별 분할)의 이중 그래프는 1879년 알프레드 켐페에 의해 언급되었고, 1891년 로타 헤프터[de]에 의해 평면이 아닌 표면의 지도까지 확장되었다.[53]추상 평면 그래프에 대한 연산으로서의 이중성은 1931년 Hasler Whitney에 의해 도입되었다.[54]

메모들

  1. ^ van Lint, J. H.; Wilson, Richard Michael (1992), A Course in Combinatorics, Cambridge University Press, p. 411, ISBN 0-521-42260-4.
  2. ^ Bóna, Miklós (2006), A walk through combinatorics (2nd ed.), World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, p. 276, doi:10.1142/6177, ISBN 981-256-885-9, MR 2361255.
  3. ^ Ziegler, Günter M. (1995), "2.3 Polarity", Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152, pp. 59–64.
  4. ^ Weisstein, Eric W., "Self-dual graph", MathWorld
  5. ^ a b Servatius, Brigitte; Christopher, Peter R. (1992), "Construction of self-dual graphs", The American Mathematical Monthly, 99 (2): 153–158, doi:10.2307/2324184, JSTOR 2324184, MR 1144356.
  6. ^ Thulasiraman, K.; Swamy, M. N. S. (2011), Graphs: Theory and Algorithms, John Wiley & Sons, Exercise 7.11, p. 198, ISBN 978-1-118-03025-7.
  7. ^ Servatius & Christopher(1992년)의 정리 5의 증거를 보라.
  8. ^ Nishizeki, Takao; Chiba, Norishige (2008), Planar Graphs: Theory and Algorithms, Dover Books on Mathematics, Dover Publications, p. 16, ISBN 978-0-486-46671-2.
  9. ^ Jensen, Tommy R.; Toft, Bjarne (1995), Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization, vol. 39, Wiley, p. 17, ISBN 978-0-471-02865-9, note that "bridge" and "loop" are dual concepts.
  10. ^ Balakrishnan, V. K. (1997), Schaum's Outline of Graph Theory, McGraw Hill Professional, Problem 8.64, p. 229, ISBN 978-0-07-005489-9.
  11. ^ a b Foulds, L. R. (2012), Graph Theory Applications, Springer, pp. 66–67, ISBN 978-1-4612-0933-1.
  12. ^ Bondy, Adrian; Murty, U.S.R. (2008), "Planar Graphs", Graph Theory, Graduate Texts in Mathematics, vol. 244, Springer, Theorem 10.28, p. 267, doi:10.1007/978-1-84628-970-5, ISBN 978-1-84628-969-9, LCCN 2007923502
  13. ^ Angelini, Patrizio; Bläsius, Thomas; Rutter, Ignaz (2014), "Testing mutual duality of planar graphs", International Journal of Computational Geometry and Applications, 24 (4): 325–346, arXiv:1303.1640, doi:10.1142/S0218195914600103, MR 3349917.
  14. ^ Diestel, Reinhard (2006), Graph Theory, Graduate Texts in Mathematics, vol. 173, Springer, p. 25, ISBN 978-3-540-26183-4.
  15. ^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990], Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, ISBN 0-262-03293-7
  16. ^ Godsil, Chris; Royle, Gordon F. (2013), Algebraic Graph Theory, Graduate Texts in Mathematics, vol. 207, Springer, Theorem 14.3.1, p. 312, ISBN 978-1-4613-0163-9.
  17. ^ Oxley, J. G. (2006), Matroid Theory, Oxford Graduate Texts in Mathematics, vol. 3, Oxford University Press, p. 93, ISBN 978-0-19-920250-8.
  18. ^ a b Cho, Jung Jin; Chen, Yong; Ding, Yu (2007), "On the (co)girth of a connected matroid", Discrete Applied Mathematics, 155 (18): 2456–2470, doi:10.1016/j.dam.2007.06.015, MR 2365057.
  19. ^ a b Hartvigsen, D.; Mardon, R. (1994), "The all-pairs min cut problem and the minimum cycle basis problem on planar graphs", SIAM Journal on Discrete Mathematics, 7 (3): 403–418, doi:10.1137/S0895480190177042.
  20. ^ Noy, Marc (2001), "Acyclic and totally cyclic orientations in planar graphs", American Mathematical Monthly, 108 (1): 66–68, doi:10.2307/2695680, JSTOR 2695680, MR 1857074.
  21. ^ Tutte, W. T. (1984), Graph theory, Encyclopedia of Mathematics and its Applications, vol. 21, Reading, MA: Addison-Wesley Publishing Company, Advanced Book Program, p. 289, ISBN 0-201-13520-5, MR 0746795.
  22. ^ Riley, T. R.; Thurston, W. P. (2006), "The absence of efficient dual pairs of spanning trees in planar graphs", Electronic Journal of Combinatorics, 13 (1): Note 13, 7, doi:10.37236/1151, MR 2255413.
  23. ^ Lyons, Russell (1998), "A bird's-eye view of uniform spanning trees and forests", Microsurveys in discrete probability (Princeton, NJ, 1997), DIMACS Ser. Discrete Math. Theoret. Comput. Sci., vol. 41, Amer. Math. Soc., Providence, RI, pp. 135–162, MR 1630412. 특히 138-139페이지를 보라.
  24. ^ Flammini, Alessandro (October 1996), Scaling Behavior for Models of River Network, Ph.D. thesis, International School for Advanced Studies, pp. 40–41.
  25. ^ Sommerville, D. M. Y. (1958), An Introduction to the Geometry of N Dimensions, Dover.
  26. ^ Eppstein, David (2003), "Dynamic generators of topologically embedded graphs", Proceedings of the 14th ACM/SIAM Symposium on Discrete Algorithms, pp. 599–608, arXiv:cs.DS/0207082.
  27. ^ Harary, Frank (1969), Graph Theory, Reading, Mass.: Addison-Wesley Publishing Co., Theorem 9.4, p. 142, MR 0256911.
  28. ^ Gross, Jonathan L.; Yellen, Jay, eds. (2003), Handbook of Graph Theory, CRC Press, p. 724, ISBN 978-1-58488-090-5.
  29. ^ He, Xin (1999), "On floor-plan of plane graphs", SIAM Journal on Computing, 28 (6): 2150–2167, doi:10.1137/s0097539796308874.
  30. ^ a b Welsh, D. J. A. (1969), "Euler and bipartite matroids", Journal of Combinatorial Theory, 6 (4): 375–377, doi:10.1016/s0021-9800(69)80033-5, MR 0237368.
  31. ^ Florek, Jan (2010), "On Barnette's conjecture", Discrete Mathematics, 310 (10–11): 1531–1535, doi:10.1016/j.disc.2010.01.018, MR 2601261.
  32. ^ Las Vergnas, Michel (1980), "Convexity in oriented matroids", Journal of Combinatorial Theory, Series B, 29 (2): 231–243, doi:10.1016/0095-8956(80)90082-9, MR 0586435.
  33. ^ Tutte, William Thomas (1953), A contribution to the theory of chromatic polynomials
  34. ^ a b di Battista, Giuseppe; Eades, Peter; Tamassia, Roberto; Tollis, Ioannis G. (1999), Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, p. 91, ISBN 978-0-13-301615-4.
  35. ^ Fleischner, Herbert J.; Geller, D. P.; Harary, Frank (1974), "Outerplanar graphs and weak duals", Journal of the Indian Mathematical Society, 38: 215–219, MR 0389672.
  36. ^ Weisstein, Eric W., "Dual Tessellation", MathWorld
  37. ^ Samet, Hanan (2006), Foundations of Multidimensional and Metric Data Structures, Morgan Kaufmann, p. 348, ISBN 978-0-12-369446-1.
  38. ^ a b Gagarin, Andrei; Kocay, William; Neilson, Daniel (2003), "Embeddings of small graphs on the torus" (PDF), Cubo, 5: 351–371, archived from the original (PDF) on 2017-02-01, retrieved 2015-08-12.
  39. ^ Nakamoto, Atsuhiro; Negami, Seiya (2000), "Full-symmetric embeddings of graphs on closed surfaces", Memoirs of Osaka Kyoiku University, 49 (1): 1–15, MR 1833214.
  40. ^ Pisanski, Tomaž; Randić, Milan (2000), "Bridges between geometry and graph theory" (PDF), in Gorini, Catherine A. (ed.), Geometry at Work, MAA Notes, vol. 53, Cambridge University Press, pp. 174–194, ISBN 9780883851647, MR 1782654
  41. ^ Jones, G. A.; Thornton, J. S. (1983), "Operations on maps, and outer automorphisms", Journal of Combinatorial Theory, Series B, 35 (2): 93–103, doi:10.1016/0095-8956(83)90065-5, MR 0733017
  42. ^ Whitney, Hassler (1932), "Non-separable and planar graphs", Transactions of the American Mathematical Society, 34 (2): 339–362, doi:10.1090/S0002-9947-1932-1501641-2.
  43. ^ Oxley, J. G. (2006), "5.2 Duality in graphic matroids", Matroid Theory, Oxford graduate texts in mathematics, vol. 3, Oxford University Press, p. 143, ISBN 978-0-19-920250-8.
  44. ^ Tutte, W. T. (2012), Graph Theory As I Have Known It, Oxford Lecture Series in Mathematics and Its Applications, vol. 11, Oxford University Press, p. 87, ISBN 978-0-19-966055-1.
  45. ^ Chorley, Richard J.; Haggett, Peter (2013), Integrated Models in Geography, Routledge, p. 646, ISBN 978-1-135-12184-6.
  46. ^ Kandel, Abraham; Bunke, Horst; Last, Mark (2007), Applied Graph Theory in Computer Vision and Pattern Recognition, Studies in Computational Intelligence, vol. 52, Springer, p. 16, ISBN 978-3-540-68020-8.
  47. ^ Devadoss, Satyan L.; O'Rourke, Joseph (2011), Discrete and Computational Geometry, Princeton University Press, p. 111, ISBN 978-1-4008-3898-1.
  48. ^ Du, Qiang; Gunzburger, Max (2002), "Grid generation and optimization based on centroidal Voronoi tessellations", Applied Mathematics and Computation, 133 (2–3): 591–607, doi:10.1016/S0096-3003(01)00260-0.
  49. ^ Piguet, Christian (2004), "7.2.1 Static CMOS Logic", Low-Power Electronics Design, CRC Press, pp. 7-1 – 7-2, ISBN 978-1-4200-3955-9.
  50. ^ Kaeslin, Hubert (2008), "8.1.4 Composite or complex gates", Digital Integrated Circuit Design: From VLSI Architectures to CMOS Fabrication, Cambridge University Press, p. 399, ISBN 978-0-521-88267-5.
  51. ^ Richeson, David S. (2012), Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton University Press, pp. 58–61, ISBN 978-1-4008-3856-1.
  52. ^ Rippmann, 마티아스(2016년),Funicular Shell설계:.기하학적 접근 방법 형태 찾기 및 이산화 케이블 카 구조물, 하빌리타치온 논문, 디스의 제작.ETH아니 23307, 취리히 연방 공과 대학교,를 대신하여 서명함. 39–40, doi:10.3929/ethz-a-010656780, hdl:20.500.11850/116926.쌍대의 평면 그래프 사이의 이 가장 오래된 삽화?또한 에릭슨, 제프(6월 9일 2016년), 제Méchanique에서 상호 힘 도표 ou Statique 피에르 드 바리 논의에 의해(1725년)확인한다.
  53. ^ Biggs, Norman; Lloyd, E. Keith; Wilson, Robin J. (1998), Graph Theory, 1736–1936, Oxford University Press, p. 118, ISBN 978-0-19-853916-2.
  54. ^ Whitney, Hassler (1931), "A theorem on graphs", Annals of Mathematics, Second Series, 32 (2): 378–390, doi:10.2307/1968197, JSTOR 1968197, MR 1503003.

외부 링크