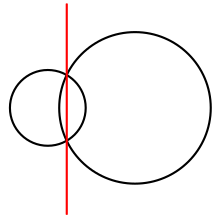
전력도

Power diagram
4개의 원으로 구성된 전원 다이어그램

계산 기하학에서 동력 다이어그램(Laguerre–Voronoi diornoi dirict cell complex, right vorichlet teselation 또는 segal dirichlet teselation)은 유클리드 평면을 원의 집합에서 정의한 다각형 셀로 분할한 것이다.주어진 원 C의 셀은 C까지의 전력 거리가 다른 원까지의 전력 거리보다 작은 모든 점으로 구성된다.동력도는 일반화된 보로노이 도표의 한 형태로, 모든 원들이 동일한 반지름을 갖는 경우 서클 중심부의 보로노이 도표와 일치한다.[1][2][3][4]

정의

주어진 원을 벗어나는 점 P의 검정력

C가 원이고 P가 C 밖의 점이라면, C에 대한 P의 힘은 P에서 C와 접하는 점 T까지의 선분할 길이의 제곱이다.동등하게 P가 원의 중심으로부터 거리 d를 가지고 있고, 원의 반지름 r을 가지고 있다면, 그 힘은 d - r이다22.동일한 공식 d2 - r은2 C의 내부 또는 외부에 있든 상관없이 평면의 모든 점으로 확장될 수 있다: C의 점들은 0의 힘을 가지며, C 내부의 점들은 음의 힘을 가진다.[2][3][4]

원 Ci 집합의 전원도는 원 C가i P의 전력을 최소화할 때마다 점 P가 R에i 속하도록 평면을 N 영역 Ri(셀이라고 함)[2][3][4]으로 분할한 것이다.

두 개의 교차하는 원의 급진적인 축.두 원의 동력도는 이 선에 의해 형성된 두 개의 반평면으로 된 평면의 분할이다.

사례 n = 2에서 전원도는 두 개의 반평면으로 구성되며, 두 원의 래디컬 축 또는 코데일이라고 하는 선으로 구분된다.급진적인 축을 따라 두 원은 동등한 힘을 갖는다.보다 일반적으로, 어떤 전력 다이어그램에서든, 각 셀i R은 볼록한 폴리곤으로, 원i C의 급진적인 축에 의해 경계된 반공간과 서로 다른 원의 교차점이다.세 개의 세포가 도표 정점에서 만나는 것은 세포가 정점에서 만나는 세 개의 원의 급진적인 중심이다.[2][3][4]

관련 구성

전원 다이어그램은 지점 사이트 집합의 보로노이 다이어그램의 가중치 형태로 보여질 수 있으며, 지점 중 하나가 다른 사이트보다 가까운 셀로 분할된다.가중 보로노이 다이어그램의 다른 형태로는 각 사이트와 다른 사이트와의 거리를 비교하기 전에 거리에 추가된 가중치를 갖는 추가 가중 가중치 보로노이 다이어그램과 부지의 가중치를 비교하기 전에 그 거리에 곱한 곱셈 가중치 보로노이 다이어그램이 있다.다른 사이트로 가는 길대조적으로 전력 다이어그램에서는 각 원의 중심부를 부지로 볼 수 있으며, 각 원의 제곱 반지름을 다른 제곱 거리와의 비교 전에 제곱 유클리드 거리에서 뺀 무게로 볼 수 있다.모든 원 반지름이 동일한 경우, 이 뺄셈은 비교에 아무런 차이가 없으며, 전력 다이어그램은 보로노이 도표와 일치한다.[3][4]

평면 전력도는 가중치가 없는 3차원 보로노이 도표의 평면 단면으로 해석할 수도 있다.이 해석에서 단면 평면의 원 중심 세트는 3차원 보로노이 현장의 수직 투영이며, 각 원의 제곱 반지름은 단면 평면에서 해당 부지의 제곱 거리를 뺀 상수 K로, 여기서 K는 이 모든 반지름을 만들 수 있을 정도로 크게 선택된다.ve.[5]

보로노이 도표처럼 동력도는 어떤 차원의 유클리드 공간으로 일반화될 수 있다.d 치수의 n 구들의 전력도는 d + 1 치수의 n 위를 향한 반공간 집합의 교차점과 일치하며, 그 반대의 경우도 마찬가지다.[3]

알고리즘 및 응용 프로그램

2차원 전력도는 시간 O(n log n)로 실행되는 알고리즘에 의해 구성될 수 있다.[2][3]보다 일반적으로는 고차원 반공간 교차로와의 동등성 때문에 d차원 전력 다이어그램(d > 2)은 시간 d/ 로 실행되는 알고리즘에 의해 구성될 수 있다[3]

전력도는 구 조합의 부피를 계산하기 위한 효율적인 알고리즘의 일부로 사용될 수 있다.각 구와 그것의 전력 다이어그램 셀을 교차시키면 전체 조합에 그 기여를 하며, 여기서부터 전력 다이어그램의 복잡성에 비례하여 볼륨이 시간 내에 계산될 수 있다.[6]

전력 다이어그램의 다른 응용 프로그램에는 점이 디스크 조합에 속하는지 여부를 테스트하기 위한 데이터 구조,[2] 디스크 조합의 경계를 구성하기 위한 알고리즘, 그리고 [2]볼 집합에서 가장 가까운 두 개의 볼을 찾기 위한 알고리즘이 포함된다.[7]

역사

아우렌해머(1987)는 19세기 수학자 에드몬드 라구에르와 게오르기 보로노이이의 작품에 대한 동력 거리의 정의를 추적한다.[3]Fejes Toth(1977)는 전원 다이어그램을 정의하고 이를 사용하여 n개의 원형 디스크 조합의 경계는 항상 최대 2n 지점 광원에서 조명될 수 있음을 보여주었다.[8]파워 다이어그램은 "라구에르-보로노이 다이어그램", "디리클레 셀 콤플렉스", "라디칼 보로노이 테셀레이션", "단면 디리클레 테셀레이션" 등 다른 이름으로 문헌에 등장했다.[9]

참조

  1. ^ Linhart, J. (1981), "Dirichletsche Zellenkomplexe mit maximaler Eckenzahl", Geometriae Dedicata, 11 (3): 363–367, doi:10.1007/BF00149360, MR 0627538.
  2. ^ a b c d e f g Imai, Hiroshi; Iri, Masao; Murota, Kazuo (1985), "Voronoĭ diagram in the Laguerre geometry and its applications", SIAM Journal on Computing, 14 (1): 93–105, doi:10.1137/0214006, MR 0774929.
  3. ^ a b c d e f g h i Aurenhammer, F. (1987), "Power diagrams: properties, algorithms and applications", SIAM Journal on Computing, 16 (1): 78–96, doi:10.1137/0216006, MR 0873251.
  4. ^ a b c d e Edelsbrunner, Herbert (1987), "13.6 Power Diagrams", Algorithms in Combinatorial Geometry, EATCS Monographs on Theoretical Computer Science, vol. 10, Springer-Verlag, pp. 327–328.
  5. ^ Ash, Peter F.; Bolker, Ethan D. (1986), "Generalized Dirichlet tessellations", Geometriae Dedicata, 20 (2): 209–243, doi:10.1007/BF00164401, MR 0833848.
  6. ^ Avis, David; Bhattacharya, Binay K.; Imai, Hiroshi (1988), "Computing the volume of the union of spheres" (PDF), The Visual Computer, 3 (6): 323–328, doi:10.1007/BF01901190.
  7. ^ Guibas, Leonidas; Zhang, Li (1998), "Euclidean proximity and power diagrams", 10th Canadian Conference on Computational Geometry.
  8. ^ Fejes Tóth, L. (1977), "Illumination of convex discs", Acta Mathematica Academiae Scientiarum Hungaricae, 29 (3–4): 355–360, doi:10.1007/BF01895856, MR 0464065.
  9. ^ Aurenhammer, F.; Imai, H. (1988), "Geometric relations among Voronoĭ diagrams", Geometriae Dedicata, 27 (1): 65–75, doi:10.1007/BF00181613, MR 0950323.