점 위치

이 기사 제목을 포인트 위치 문제로 변경해 달라는 요청이 논의 중입니다.토론이 종료될 때까지 이 기사를 이동하지 마십시오.

점 위치 문제는 계산 기하학의 기본 주제입니다.컴퓨터 그래픽, 지리 정보 시스템(GIS), 모션 플래닝 및 CAD(Computer Aided Design) 등 기하학적 데이터를 처리하는 영역에서 응용 프로그램을 찾습니다.

가장 일반적인 형태에서 문제는 공간을 분리된 영역으로 분할하는 경우 쿼리 포인트가 있는 영역을 결정하는 것입니다.예를 들어, 그래픽 사용자 인터페이스의 어떤 창에 주어진 마우스 클릭이 포함되어 있는지 결정하는 문제는 각 창의 보이는 부분에 의해 형성된 하위 구분으로 점 위치의 인스턴스로 공식화될 수 있습니다.특수 데이터 구조가 이 ^[1]애플리케이션의 범용 포인트 위치 데이터 구조보다 더 적합할 수도 있습니다.또 다른 특별한 경우는 점이 단일 폴리곤의 안쪽, 바깥쪽 또는 경계에 있는지 확인해야 하는 폴리곤 문제의 점입니다.

많은 응용프로그램에서 공간의 동일한 파티션에 대해 여러 다른 점의 위치를 결정해야 합니다.이 문제를 효율적으로 해결하려면 쿼리 포인트가 주어지면 쿼리 포인트가 포함된 영역을 신속하게 결정하는 데이터 구조를 구축하는 것이 유용합니다(예: Voronoi Diagram).

평면 케이스

평면의 경우, 우리는 면이라고 불리는 여러 다각형으로 형성된 평면 분할 S가 주어지며, 어떤 면에 질의점이 있는지 결정해야 합니다.Point-in-Polygon 알고리즘을 사용하여 각 면에 대한 브루트 포스 검색이 가능하지만, 일반적으로 복잡도가 높은 부분에서는 불가능합니다.O(n) 저장 공간과 O(log n) 쿼리 시간을 갖는 최적의 데이터 구조로 이어지는 몇 가지 다른 접근 방식. 여기서 n은 S의 총 정점 수입니다.단순화를 위해 평면 분할이 사각형 경계 상자 안에 포함되어 있다고 가정합니다.

슬래브 분해

1976년에 Dobkin과 Lipton이 O(log n) 시간을 달성한 가장 간단하고 초기의 데이터 구조를 발견했습니다.S의 각 정점을 통과하는 수직선을 사용하여 S를 세분화하는 것을 기준으로 합니다.두 개의 연속된 수직선 사이의 영역을 슬래브라고 합니다.각 슬래브는 슬래브를 왼쪽에서 오른쪽으로 완전히 교차하는 교차하지 않는 선 세그먼트로 구분됩니다.슬래브 내부의 연속된 두 세그먼트 사이의 영역은 S의 고유한 면에 해당합니다.따라서 점 위치 문제를 두 가지 간단한 ^[2]문제로 줄입니다.

1. 평면을 수직 슬래브로 세분화하면 지정된 점을 포함하는 슬래브를 결정합니다.
2. 슬래브를 왼쪽에서 오른쪽으로 완전히 교차하는 교차하지 않는 세그먼트에 의해 영역으로 세분된 슬래브가 주어지면 지정된 점을 포함하는 영역을 결정합니다.

첫 번째 문제는 O(log n) 시간에 수직선의 x 좌표에 대한 이진 검색으로 해결할 수 있습니다.두 번째 문제는 이진 검색을 통해 O(log n) 시간 내에 해결할 수도 있습니다.세그먼트가 슬래브와 교차하지 않고 완전히 교차하므로 세그먼트를 각 슬래브 내에서 수직으로 정렬할 수 있습니다.이 알고리즘을 사용하면 로그 시간 내에 점 위치를 지정할 수 있고 구현이 쉽지만, 각 슬래브가 ^[2]세그먼트의 상당 부분을 교차할 수 있기 때문에 슬래브와 슬래브 내에 포함된 영역을 구축하는 데 필요한 공간은 O(n²)만큼 클 수 있습니다.

몇몇 저자들은 인접한 두 개의 슬래브를 가로지르는 세그먼트가 대부분 같다는 것을 알아냈습니다.따라서 데이터 구조의 크기가 상당히 줄어들 수 있습니다.보다 구체적으로 Sarnak 및 Tarjan은 평면 위에서 왼쪽에서 오른쪽으로 수직선 l을 스위프하면서 지속적인 빨간색-검은 트리에서 교차하는 세그먼트를 유지합니다.이를 통해 O(log n) 쿼리 시간을 ^[3]유지하면서 스토리지 공간을 O(n)로 줄일 수 있습니다.

모노톤 부분군

(수직) 모노톤 체인은 y 좌표가 경로를 따라 증가하지 않는 경로입니다.단순 다각형은 첫 번째 정점과 마지막 정점이 공통적으로 있는 두 개의 모노톤 체인으로 형성된 경우 (수직) 모노톤입니다.모든 면을 단조롭게 만들기 위해 평면 분할에 일부 모서리를 추가하여 단조 분할이라고 하는 것을 얻을 수 있습니다.이 프로세스는 분할에 정점을 추가하지 않으며(따라서 크기는 O(n)) 평면 스위프로 O(n log n) 시간에 수행할 수 있습니다(다각형 삼각형을 사용하여 선형 시간으로 수행할 수도 있음).따라서 이 섹션에서와 같이 데이터 구조를 모노톤 세분화의 경우로 제한하면 일반성이 손실되지 않습니다.

슬래브 분해의 단점은 수직선이 분해에 추가 세그먼트를 생성하여 O(n) 저장 공간을 확보하기 어렵다는 것입니다.Herbert Edelsbrunner, Leonidas J. Guibas 및 Jorge Stolfi는 단조로운 세분화에서 가장자리만 사용하는 최적의 데이터 구조를 발견했습니다.이 개념은 수직선을 사용하여 ^[4]분할하는 대신 수직 모노톤 체인을 사용하는 것입니다.

이 일반적인 아이디어를 실제 효율적인 데이터 구조로 변환하는 것은 간단한 작업이 아닙니다.첫째, 우리는 유사한 크기의 두 부분으로 분할하는 모노톤 체인을 계산할 수 있어야 합니다.둘째, 일부 에지는 여러 모노톤 체인에 포함될 수 있으므로 저장 공간이 O(n)인지 확인하도록 주의해야 합니다.셋째, 점이 단조로운 부분군의 왼쪽에 있는지 또는 오른쪽에 있는지 여부를 검사하는 것은 ^[4]순진하게 수행될 경우 O(n) 시간이 걸립니다.

처음 두 가지 문제를 해결하는 방법에 대한 자세한 내용은 이 기사의 범위를 벗어납니다.우리는 세 번째 문제를 다루는 방법을 간략하게 언급합니다.이진 검색을 사용하여 점이 단조 체인의 왼쪽 또는 오른쪽에 있는지 O(log n) 시간으로 테스트할 수 있습니다.점 위치를 실제로 확인하려면 O(log n) 체인을 통해 또 다른 중첩 이진 검색을 수행해야 하므로 쿼리 시간은 O(log² n)입니다.O(log n) 쿼리 시간을 달성하려면 서로 다른 모노톤 ^[4]체인의 가장자리 사이에 포인터를 유지하는 분수 계단식을 사용해야 합니다.

삼각측량 정제

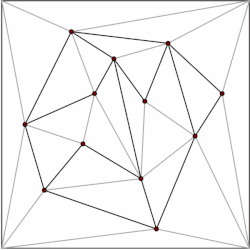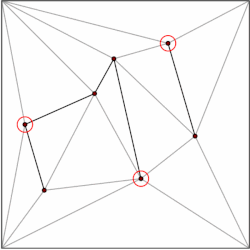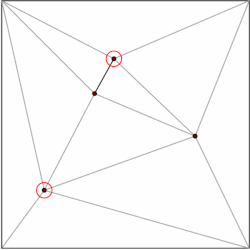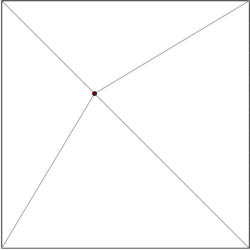
정점이 m개인 다각형은 m-2개의 삼각형으로 분할할 수 있습니다.이것은 삼각형에서 시작하여 유도로 나타낼 수 있습니다.다각형을 효율적으로 삼각형화하기 위한 수많은 알고리즘이 있으며, 가장 빠른 O(n) 최악의 경우 시간을 갖습니다.따라서 분할의 각 다각형을 삼각형으로 분해하고 데이터 구조를 삼각형으로만 구성된 분할의 경우로 제한할 수 있습니다.Kirkpatrick은 O(n) 저장 공간과 O(log n) 쿼리 ^[5]시간을 사용하여 삼각형 세그먼트에서 점 위치에 대한 데이터 구조를 제공합니다.

일반적인 아이디어는 삼각형의 계층 구조를 만드는 것입니다.쿼리를 수행하기 위해 쿼리 포인트가 포함된 최상위 삼각형을 찾는 것으로 시작합니다.최상위 삼각형의 수는 상수로 제한되므로 O(1) 시간 내에 이 작업을 수행할 수 있습니다.각 삼각형에는 계층의 다음 수준에서 교차하는 삼각형에 대한 포인터가 있으며 포인터 수도 상수로 제한됩니다.우리는 ^[5]수준별로 쿼리 포인트 레벨을 포함하는 삼각형을 찾아 쿼리를 진행합니다.

데이터 구조는 반대 순서, 즉 상향식으로 구성됩니다.삼각형 분할부터 시작하여 제거할 독립적인 정점 집합을 선택합니다.정점을 제거한 후, 우리는 세분화를 다시 세분화합니다.분할은 삼각형으로 형성되므로 그리디 알고리즘은 정점의 일정 부분을 포함하는 독립 집합을 찾을 수 있습니다.따라서 제거 단계 수는 O(log n)^[5]입니다.

사다리꼴 분해

이 문제에 대한 무작위 접근법은 사다리꼴 분해 또는 사다리꼴 지도를 기반으로 합니다.사다리꼴 분해는 원래 세분화의 각 정점에서 위와 아래로 가는 수직 탄환을 쏘는 것입니다.총알은 가장자리에 부딪히면 멈추고, 부분에 새로운 가장자리를 형성합니다.이러한 방식으로, 우리는 원래 세분화의 각 정점에 대해 두 개의 새로운 정점만 추가하고 가장자리 수를 네 ^[6]개 증가시키기 때문에 O(n) 모서리와 정점만 가진 슬래브 분해의 하위 집합을 얻습니다.

사다리꼴 분해는 원래 하위 세그먼트의 세그먼트를 무작위 순서로 하나씩 추가하여 구성할 수 있습니다.처음에는 (세그먼트가 추가되기 전에) 사다리꼴 분해는 분할의 경계 상자인 단일 사다리꼴로 구성됩니다.각 후속 단계는 점 위치 쿼리를 사용하여 현재 사다리꼴 분해 내에서 다음 라인 세그먼트의 한 끝점을 찾은 다음, 결과 사다리꼴에서 동일한 세그먼트를 포함하는 인접 사다리꼴로 이동하여 세분화 및 재결합하여 정제된 분해를 형성합니다.이러한 종류의 무작위 증분 기하학 알고리즘에 일반적으로 사용되는 분석의 한 형태인 역방향 분석은 각 삽입에 대해 생성되는 예상되는 트라페주스 수가 상수에 의해 제한된다는 것을 보여줍니다. 따라서 이 알고리즘의 총 단계 수는 점 위치 밖에서 ^[6]선형입니다.

이 알고리즘 내에서 수행되는 현재 세분화의 점 위치는 알고리즘의 끝에서 최종 사다리꼴 분해에서 점 위치 쿼리에 사용할 수 있는 동일한 구조를 사용하여 수행할 수 있습니다.이 점 위치 데이터 구조는 방향 비순환 그래프의 형태를 취합니다. 여기서 정점은 정제의 특정 시점에 존재했던 사다리꼴이고 방향이 지정된 가장자리는 정제에서 더 이상 존재하지 않는 각 사다리꼴을 대체한 사다리꼴에 연결합니다.점 위치 쿼리는 이 그래프의 경로를 따라 초기 사다리꼴에서 시작하여 대체되지 않은 사다리꼴에 도달할 때까지 각 단계에서 쿼리 점을 포함하는 대체 사다리꼴을 선택하여 수행됩니다.이 디그래프의 예상 검색 깊이는 쿼리 지점에서 시작하여 O(log n)입니다.데이터 구조의 공간은 이 정제 과정에서 생성된 트라페주스의 수에 비례하며, 예상치는 O(n)^[6]입니다.

고차원

이 섹션에서는 어떤 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션을 개선할 수 있도록 도와주시기 바랍니다. 소스가 없는 재료는 문제가 발생하여 제거될 수 있습니다.(2023년 8월) (이 템플릿 메시지를 제거하는 방법 및 시기에 대해 알아보십시오.)

2보다 큰^{[citation needed]} 차원에 대해 선형 공간과 로그 쿼리 시간을 갖는 알려진 일반 점 위치 데이터 구조가 없습니다.따라서 쿼리 시간 또는 스토리지 공간을 희생하거나 일반적이지 않은 세분화 유형으로 제한해야 합니다.

3차원 공간에서는 O(n log n) 공간을 사용하여 O(log² n)의 점 위치 쿼리에 응답할 수 있습니다.일반적인 아이디어는 각 분할 정점을 포함하는 n개의 평행 평면과 분할의 교차점에 해당하는 여러 평면 점 위치 데이터 구조를 유지하는 것입니다.이 아이디어를 단순하게 사용하면 스토리지 공간이 O(n²)로 증가합니다.슬래브 분해에서와 동일한 방식으로 연속 데이터 구조 간의 유사성을 활용하여 저장 공간을 O(n log n)로 줄일 수 있지만 쿼리 시간은 O(log² n)^{[citation needed]}로 증가합니다.

d차원 공간에서 점 위치는 면을 (d-1)차원 공간에 재귀적으로 투영하여 해결할 수 있습니다.쿼리 시간이 O(log n)인 동안 저장 공간은 O${\displaystyle ({{n2}^{}}^{}}$d$){displaystyle$ O$(n^{2^{d$$만큼{\displaystyle }$ 높을 수 있습니다.d차원 데이터 구조의 높은 복잡성은 특별한 유형의 세분화에 대한 연구로 이어졌습니다.

한 가지 중요한 예는 초평면 배열의 경우입니다.n개의 초평면 배열은 O(n^d) 셀을 정의하지만, 점 위치는 Chazelle의 계층적 절단을 사용하여 O(n^d) 공간으로 O(log n) 시간에 수행할 수 있습니다.

또 다른 특별한 유형의 분할을 직선 분할(또는 직교 분할)이라고 합니다.직선 분할에서 모든 모서리는 직교 축 중 하나와 평행합니다.이 경우 점 위치는 O(n) 공간으로 O(log^d-1 n) 시간으로 응답할 수 있습니다.

레퍼런스

메모들

원천

• de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2000). "Chapter 6: Point location". Computational Geometry (2nd revised ed.). Springer-Verlag. pp. 121–146. ISBN 3-540-65620-0.
• Bern, Marshall (1990). "Hidden surface removal for rectangles". Journal of Computer and System Sciences. 40 (1): 49–69. doi:10.1016/0022-0000(90)90018-G. MR 1047289.
• Dobkin, David; Lipton, Richard J. (1976). "Multidimensional searching problems". SIAM Journal on Computing. 5 (2): 181–186. doi:10.1137/0205015.
• Edelsbrunner, Herbert; Guibas, Leonidas J.; Stolfi, Jorge (1986). "Optimal point location in a monotone subdivision". SIAM Journal on Computing. 15 (2): 317–340. doi:10.1137/0215023.
• Kirkpatrick, David G. (1983). "Optimal search in planar subdivisions". SIAM Journal on Computing. 12 (1): 28–35. CiteSeerX 10.1.1.461.1866. doi:10.1137/0212002.
• Sarnak, Neil; Tarjan, Robert E. (1986). "Planar point location using persistent search trees". Communications of the ACM. 29 (7): 669–679. doi:10.1145/6138.6151.

진일보한 내용

• Snoeyink, Jack (2004). "Chapter 34: "Point Location". In Goodman, Jacob E.; O'Rourke, Joseph (eds.). Handbook of Discrete and Computational Geometry (2nd ed.). Chapman & Hall/CRC. ISBN 1-58488-301-4.

외부 링크

• 스토니브룩 대학교의 점 위치 소스 저장소
• 계산기하학 알고리즘 라이브러리인 CGAL의 점 위치 쿼리