로이드 알고리즘

전기공학과 컴퓨터 공학에서 보로노이 반복 또는 이완으로도 알려진 로이드의 알고리즘은 스튜어트 P의 이름을 딴 알고리즘입니다. 유클리드 공간의 부분 집합과 이 부분 집합의 파티션에서 균일한 간격의 점 집합을 잘 모양으로 균일한 크기의 볼록 셀로 찾기 위한 로이드.^[1] 밀접하게 연관된 k-평균 클러스터링 알고리즘처럼 파티션에서 각 집합의 중심점을 반복적으로 찾은 다음 이 중심점 중 어떤 것이 가장 가까운지에 따라 입력을 다시 분할합니다. 이 설정에서 평균 연산은 공간 영역에 대한 적분이며 가장 가까운 중심 연산은 보로노이 다이어그램으로 나타납니다.

알고리즘이 유클리드 평면에 가장 직접적으로 적용될 수 있지만, 유사한 알고리즘이 고차원 공간이나 다른 비유클리드 메트릭이 있는 공간에도 적용될 수 있습니다. Lloyd의 알고리즘을 사용하여 입력의 중심 보로노이트 셀레이션에 근접한 근사치를 구성할 수 있으며,^[2] 이는 양자화, 디더링 및 스티플링에 사용될 수 있습니다. Lloyd 알고리즘의 다른 응용으로는 유한요소법에서 삼각형 메쉬를 평활화하는 것이 있습니다.

로이드 알고리즘의 예입니다. 각 반복 시 현재 사이트 위치(빨간색)의 Voronoi 다이어그램이 표시됩니다. 회색 원은 보로노이 세포의 중심을 나타냅니다.

반복1

반복 2

반복 3

15번 반복

마지막 이미지에서 이 부위는 보로노이 세포의 중심부 근처에 있습니다. 중심 보로노이테 셀레이션이 발견되었습니다.

역사

이 알고리즘은 스튜어트 P에 의해 처음 제안되었습니다. 1957년 펄스-코드 변조 기술로서 벨 연구소의 로이드. 로이드의 작품은 널리 유통되었지만 1982년까지 출판되지 않았습니다.^[1] 비슷한 알고리즘을 조엘 맥스가 독자적으로 개발하여 1960년에 발표했는데,^[3] 그래서 이 알고리즘을 로이드-맥스 알고리즘이라고 부르기도 합니다.

알고리즘설명

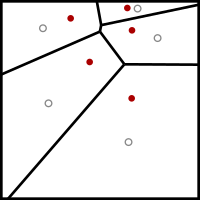
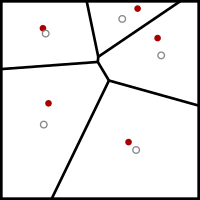
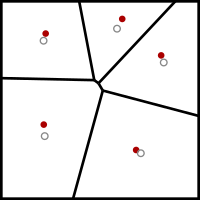
Lloyd 알고리즘은 입력 도메인에서 몇 k개의 점 사이트를 초기에 배치하는 것으로 시작합니다. 매쉬-스무딩 애플리케이션에서는 매쉬될 매쉬의 꼭짓점이 됩니다. 다른 애플리케이션에서는 임의로 또는 적절한 크기의 균일한 삼각형 매쉬와 입력 도메인을 교차하여 배치할 수 있습니다.

그런 다음 다음 이완 단계를 반복적으로 실행합니다.

k개 사이트의 보로노이 다이어그램이 계산됩니다.
보로노이 다이어그램의 각 셀이 통합되고 중심이 계산됩니다.
그런 다음 각 부위는 보로노이 세포의 중심부로 이동됩니다.

적분 및 중심 계산

보로노이 다이어그램 구성 알고리즘은 특히 2개 이상의 차원의 입력의 경우 매우 사소하지 않을 수 있기 때문에 이 다이어그램을 계산하고 셀의 정확한 중심체를 찾는 단계는 근사치로 대체될 수 있습니다.

근사

일반적인 단순화는 그래픽 하드웨어의 텍스처 버퍼와 같은 미세한 픽셀 그리드와 같은 공간의 적절한 이산화를 사용하는 것입니다. 세포는 해당 사이트 ID로 레이블이 지정된 픽셀로 구체화됩니다. 셀의 새 중심은 동일한 레이블로 할당된 모든 픽셀의 위치를 평균하여 근사화됩니다. 또는 일부 고정된 기본 확률 분포에 따라 랜덤 샘플 포인트가 생성되고 가장 가까운 사이트에 할당되며 각 사이트의 중심에 근사하도록 평균화되는 몬테카를로 방법을 사용할 수 있습니다.

정확한 계산

다른 공간에 임베딩하는 것도 가능하지만, 이 정교화는 L² 규범을 사용하여 유클리드 공간을 가정하고 가장 관련성이 높은 두 가지 시나리오, 즉 2차원과 3차원에 대해 논의합니다.

보로노이 세포는 볼록한 모양이며 항상 그 자리를 둘러싸기 때문에, 간단한 분해가 가능합니다.

2차원에서 다각형 셀의 가장자리는 그 자리와 연결되어 우산 모양의 삼각형 집합을 만듭니다.
3차원에서 셀은 여러 개의 평면 다각형으로 둘러싸여 있으며, 이 다각형은 먼저 삼각형이 되어야 합니다.
- 다각형 면의 중심(예: 모든 정점의 평균)을 계산합니다.
- 다각형 면의 꼭짓점을 중심과 연결하면 평면 우산 모양의 삼각형이 됩니다.
- 세 번째로, 세포의 선체의 삼각형과 세포의 위치를 연결하여 사면체 집합을 얻습니다.

세포의 통합과 중심(질량 중심)의 계산은 이제 단순한 중심의 가중 조합으로 제공됩니다(다음에서 ${\textstyle \mathbf {c} _{i}}$ ${\$ 라고 함). ${\textstyle \mathbf {c} _{i}}$

두 가지 차원:
- 삼각형의 경우 중심은 예를 들어 직각좌표를 사용하여 쉽게 계산할 수 있습니다.
- 가중치는 단순 x 대 셀 면적 비율로 계산됩니다.
3차원:
- 정사면체의 중심은 3개의 이등분 평면의 교점으로 발견되며 행렬-벡터 곱으로 표현될 수 있습니다.
- 가중치는 단순 x 대 셀 부피 비율로 계산됩니다.

$n개$ 의 삼각형 단순화와 누적 면적 ${\textstyle A_{C}=\sum _{i=0}^{n}a_{i}}$ ${\textstyle A_{C}=\sum _{i=0}^{n}a_{i}}$ = ∑ ${\textstyle A_{C}=\sum _{i=0}^{n}a_{i}}$ = ${\textstyle A_{C}=\sum _{i=0}^{n}a_{i}}$ 0 ${\textstyle A_{C}=\sum _{i=0}^{n}a_{i}}$ $na$ {\ $textstyle$ A_{C} =\sum _{i=0}^{n}a_{i}}(여기서 i {\textstyle a_{i}}는 삼각형 단순화의 면적)의 경우, 새로운 셀 중심체는 다음과 같이 계산됩니다.

C={\frac {1}{A_{C}}}\sum _{i=0}^{n}\mathbf {c} _{i}a_{i}

마찬가지로 ${\textstyle V_{C}=\sum _{i=0}^{n}v_{i}}$ ${\textstyle V_{C}=\sum _{i=0}^{n}v_{i}}$ = ∑ ${\textstyle V_{C}=\sum _{i=0}^{n}v_{i}}$ = ${\textstyle V_{C}=\sum _{i=0}^{n}v_{i}}$ 0 n v $v$ v {\ $textstyle$ V_{C} =\sum _{i=0}^{n}v_{i}}의 부피를 갖는 3D 셀의 경우 중심체는 다음과 같이 계산됩니다.

C={\frac {1}{V_{C}}}\sum _{i=0}^{n}\mathbf {c} _{i}v_{i}

수렴

이완 단계가 수행될 때마다 점들은 약간 더 균일한 분포로 남습니다. 가까운 거리에 있는 점들은 더 멀리 떨어져 있고, 넓은 거리에 있는 점들은 더 가까이 있습니다. 일 차원에서, 이 알고리즘은 중심 보로노이 다이어그램으로 수렴하는 것으로 나타났으며, 중심 보로노이 다이어그램이라고도 합니다.^[4] 더 높은 차원에서 약간 더 약한 수렴 결과가 알려져 있습니다.^[5]^[6]

알고리즘이 느리게 수렴하거나 수치 정밀도의 한계로 인해 수렴하지 않을 수 있습니다. 따라서 로이드 알고리즘의 실제 응용은 일반적으로 분포가 "충분히 양호"하면 중단됩니다. 한 가지 일반적인 종료 기준은 반복에서 임의의 사이트에 의해 이동된 최대 거리가 미리 설정된 임계값 아래로 떨어질 때 중지하는 것입니다. 수렴은 각 점을 질량 중심까지의 거리의 ω배로 이동시킴으로써 수행되며, 일반적으로 ω에 대해 2보다 약간 작은 값을 사용하여 점들을 과도하게 완화함으로써 가속화될 수 있습니다.

적용들

Lloyd의 방법은 원래 스칼라 양자화를 위해 사용되었지만 벡터 양자화를 위해서도 방법이 확장되는 것은 분명합니다. 이처럼 정보 이론의 데이터 압축 기법에 광범위하게 사용됩니다. Lloyd의 방법은 컴퓨터 그래픽에서 사용되는데, 그 이유는 결과 분포가 파란색 노이즈 특성을 가지고 있기 때문입니다(소음의 색상도 참조). 즉, 인공물로 해석될 수 있는 저주파 성분이 거의 없다는 것을 의미합니다. 특히 디더링을 위한 샘플 위치를 선택하는 데 적합합니다. 로이드의 알고리즘은 점묘법으로 점묘도를 생성하는 데에도 사용됩니다.^[8] 이 애플리케이션에서는 입력 이미지와 일치하는 스티커 일러스트를 생성하기 위해 기준 이미지를 기준으로 중심체를 가중할 수 있습니다.^[9]

유한요소법에서는 복잡한 기하학적 구조를 가진 입력 도메인을 더 단순한 모양을 가진 요소로 분할하고, 예를 들어 2차원 도메인(유클리드 평면의 부분집합 또는 3차원 표면)은 종종 삼각형으로 분할됩니다. 유한요소법의 수렴을 위해서는 이 요소들이 잘 형성되는 것이 중요한데, 삼각형의 경우에는 정삼각형에 가까운 요소를 선호하는 경우가 많습니다. 로이드의 알고리즘은 다른 알고리즘에 의해 생성된 메쉬를 매끄럽게 하고, 그 정점을 이동시키고 그 요소들 사이의 연결 패턴을 변화시켜 더 밀접하게 정삼각형을 만들 수 있습니다.^[10] 이러한 응용 프로그램은 일반적으로 메쉬의 여러 부분에서 요소 크기의 차이와 같은 메쉬의 다른 기능을 보존하기 위해 Lloyd 알고리즘의 더 적은 수의 반복을 사용하여 수렴을 중지합니다. 다른 스무딩 방법인 라플라시안 스무딩(메쉬 꼭짓점이 이웃의 위치의 평균으로 이동되는)과 달리 로이드의 알고리즘은 메쉬의 토폴로지를 변경하여 라플라시안 스무딩으로 발생할 수 있는 엉킴 문제를 피할 수 있을 뿐만 아니라 보다 등각적인 요소로 이어질 수 있습니다. 그러나 라플라시안 스무딩은 삼각형이 아닌 요소가 있는 메쉬에 보다 일반적으로 적용할 수 있습니다.

서로 다른 거리

로이드 알고리즘은 유클리드 공간에서 주로 사용됩니다. 유클리드 거리는 알고리즘에서 두 가지 역할을 합니다: 보로노이 세포를 정의하는 데 사용되지만, 중심은 세포의 지점까지의 평균 제곱 유클리드 거리를 최소화하는 지점이기 때문에 중심을 각 세포의 대표 지점으로 선택하는 것에도 해당합니다. 대체 거리 및 중심점보다 대체 중심점을 사용할 수 있습니다. 예를 들어, Hausner(2001)는 맨해튼 메트릭의 변형(지역적으로 방향이 다른)을 사용하여 이미지의 특성과 방향이 일치하는 대략 정사각형 타일에 의한 이미지 타일을 찾았고, 이를 사용하여 타일 모자이크의 구성을 시뮬레이션했습니다.^[11] 이 응용 분야에서 Hausner는 미터법을 다양하게 사용했음에도 불구하고 계속해서 중심체를 보로노이 세포의 대표 지점으로 사용했습니다. 그러나 유클리드와 더 큰 차이가 있는 측정 기준의 경우 중심 대신 평균 제곱 거리의 최소화자를 대표 점으로 선택하는 것이 적절할 수 있습니다.^[12]

참고 항목

벡터 양자화를 위한 이 알고리즘의 일반화인 Linde-Buzo-Gray 알고리즘
기하학적 공간에서 균일한 간격의 점을 생성하기 위한 다른 방법인 가장 먼 첫 번째 횡단
밀도함수의 최대치를 구하는 관련 방법인 평균 이동
K-means++

참고문헌

^ ^a ^b Lloyd, Stuart P. (1982), "Least squares quantization in PCM", IEEE Transactions on Information Theory, 28 (2): 129–137, doi:10.1109/TIT.1982.1056489, S2CID 10833328.
^ Du, Qiang; Faber, Vance; Gunzburger, Max (1999), "Centroidal Voronoi tessellations: applications and algorithms", SIAM Review, 41 (4): 637–676, Bibcode:1999SIAMR..41..637D, doi:10.1137/S0036144599352836.
^ Max, Joel (1960), "Quantizing for minimum distortion", IRE Transactions on Information Theory, 6 (1): 7–12, doi:10.1109/TIT.1960.1057548.
^ Du, Qiang; Emelianenko, Maria; Ju, Lili (2006), "Convergence of the Lloyd algorithm for computing centroidal Voronoi tessellations", SIAM Journal on Numerical Analysis, 44: 102–119, CiteSeerX 10.1.1.591.9903, doi:10.1137/040617364.
^ Sabin, M. J.; Gray, R. M. (1986), "Global convergence and empirical consistency of the generalized Lloyd algorithm", IEEE Transactions on Information Theory, 32 (2): 148–155, doi:10.1109/TIT.1986.1057168.
^ Emelianenko, Maria; Ju, Lili; Rand, Alexander (2009), "Nondegeneracy and Weak Global Convergence of the Lloyd Algorithm in R^d", SIAM Journal on Numerical Analysis, 46: 1423–1441, doi:10.1137/070691334.
^ 샤오, 샤오. "중심 보로노이트 판매 계산을 위한 과도한 완화 로이드 방법."(2010).
^ Deussen, Oliver; Hiller, Stefan; van Overveld, Cornelius; Strothotte, Thomas (2000), "Floating points: a method for computing stipple drawings", Computer Graphics Forum, 19 (3): 41–50, doi:10.1111/1467-8659.00396, S2CID 142991, Proceedings of Eurographics.
^ Secord, Adrian (2002), "Weighted Voronoi stippling", Proceedings of the Symposium on Non-Photorealistic Animation and Rendering (NPAR), ACM SIGGRAPH, pp. 37–43, doi:10.1145/508530.508537, S2CID 12153589.
^ Du, Qiang; Gunzburger, Max (2002), "Grid generation and optimization based on centroidal Voronoi tessellations", Applied Mathematics and Computation, 133 (2–3): 591–607, CiteSeerX 10.1.1.324.5020, doi:10.1016/S0096-3003(01)00260-0.
^ Hausner, Alejo (2001), "Simulating decorative mosaics", Proceedings of the 28th annual conference on Computer graphics and interactive techniques, ACM SIGGRAPH, pp. 573–580, doi:10.1145/383259.383327, S2CID 7188986.
^ Dickerson, Matthew T.; Eppstein, David; Wortman, Kevin A. (2010), "Planar Voronoi diagrams for sums of convex functions, smoothed distance and dilation", Proc. 7th International Symposium on Voronoi Diagrams in Science and Engineering (ISVD 2010), pp. 13–22, arXiv:0812.0607, doi:10.1109/ISVD.2010.12, S2CID 15971504.

외부 링크

DemoGNG.js LBG 알고리즘 및 기타 모델을 위한 그래픽 자바스크립트 시뮬레이터, 보로노이 영역 표시 포함

[l82-1] Lloyd, Stuart P. (1982), "Least squares quantization in PCM", IEEE Transactions on Information Theory, 28 (2): 129–137, doi:10.1109/TIT.1982.1056489, S2CID 10833328.

[dfg99-2] Du, Qiang; Faber, Vance; Gunzburger, Max (1999), "Centroidal Voronoi tessellations: applications and algorithms", SIAM Review, 41 (4): 637–676, Bibcode:1999SIAMR..41..637D, doi:10.1137/S0036144599352836.

[m60-3] Max, Joel (1960), "Quantizing for minimum distortion", IRE Transactions on Information Theory, 6 (1): 7–12, doi:10.1109/TIT.1960.1057548.

[dej06-4] Du, Qiang; Emelianenko, Maria; Ju, Lili (2006), "Convergence of the Lloyd algorithm for computing centroidal Voronoi tessellations", SIAM Journal on Numerical Analysis, 44: 102–119, CiteSeerX 10.1.1.591.9903, doi:10.1137/040617364.

[sg86-5] Sabin, M. J.; Gray, R. M. (1986), "Global convergence and empirical consistency of the generalized Lloyd algorithm", IEEE Transactions on Information Theory, 32 (2): 148–155, doi:10.1109/TIT.1986.1057168.

[ejr09-6] Emelianenko, Maria; Ju, Lili; Rand, Alexander (2009), "Nondegeneracy and Weak Global Convergence of the Lloyd Algorithm in R^d", SIAM Journal on Numerical Analysis, 46: 1423–1441, doi:10.1137/070691334.

[7] 샤오, 샤오. "중심 보로노이트 판매 계산을 위한 과도한 완화 로이드 방법."(2010).

[dhos00-8] Deussen, Oliver; Hiller, Stefan; van Overveld, Cornelius; Strothotte, Thomas (2000), "Floating points: a method for computing stipple drawings", Computer Graphics Forum, 19 (3): 41–50, doi:10.1111/1467-8659.00396, S2CID 142991, Proceedings of Eurographics.

[s02-9] Secord, Adrian (2002), "Weighted Voronoi stippling", Proceedings of the Symposium on Non-Photorealistic Animation and Rendering (NPAR), ACM SIGGRAPH, pp. 37–43, doi:10.1145/508530.508537, S2CID 12153589.

[dg02-10] Du, Qiang; Gunzburger, Max (2002), "Grid generation and optimization based on centroidal Voronoi tessellations", Applied Mathematics and Computation, 133 (2–3): 591–607, CiteSeerX 10.1.1.324.5020, doi:10.1016/S0096-3003(01)00260-0.

[h01-11] Hausner, Alejo (2001), "Simulating decorative mosaics", Proceedings of the 28th annual conference on Computer graphics and interactive techniques, ACM SIGGRAPH, pp. 573–580, doi:10.1145/383259.383327, S2CID 7188986.

[dew10-12] Dickerson, Matthew T.; Eppstein, David; Wortman, Kevin A. (2010), "Planar Voronoi diagrams for sums of convex functions, smoothed distance and dilation", Proc. 7th International Symposium on Voronoi Diagrams in Science and Engineering (ISVD 2010), pp. 13–22, arXiv:0812.0607, doi:10.1109/ISVD.2010.12, S2CID 15971504.

[1]

[2]

[3]

[4]

[5]

[6]

[8]

[9]

[10]

[11]

[12]

Search