그뢰브너 기저

그뢰브너 기저(Göbner basis)는 수학에서, 특히 컴퓨터 대수학, 계산 대수 기하학, 계산 교환 대수학에서, K장 위의 다항식환 K[x₁, ..., x_n]에서 이상의 집합을 생성하는 특별한 종류입니다. 그뢰브너 기반은 이상적이고 관련된 대수적 다양성의 많은 중요한 속성들을 쉽게 추론할 수 있게 해줍니다. 예를 들어, 차원과 유한한 경우의 0의 수. 그뢰브너 기초 계산은 다항식의 시스템을 해결하고 투영 또는 유리 지도 아래 대수적 다양성의 이미지를 계산하기 위한 주요 실용적인 도구 중 하나입니다.

그뢰브너 기반 계산은 다항식 최대 공약수를 계산하기 위한 유클리드 알고리즘과 선형 시스템에 대한 가우스 제거의 다변량 비선형 일반화로 볼 수 있습니다.^[1]

브루노 부흐베르거(Bruno Buchberger)는 1965년 박사 논문에서 그뢰브너 염기를 소개했는데, 여기에 그 염기를 계산하는 알고리즘도 포함되어 있습니다(부흐베르거의 알고리즘). 그는 그들의 이름을 그의 고문 볼프강 그뢰브너의 이름을 따서 지었습니다. 2007년, 부흐베르거는 이 연구로 컴퓨터 기계 협회의 파리 카넬라키스 이론 및 실습 상을 받았습니다. 하지만, 러시아 수학자 니콜라이 귄터는 1913년에 비슷한 개념을 소개했고, 다양한 러시아 수학 저널에 실렸습니다. 이 논문들은 1987년 Bodo Reenschuch 등에 의해 재발견되기 전까지 수학계에 의해 대체로 무시되었습니다.^[2] 다변량 멱급수에 대한 유사한 개념은 1964년 히로나카 헤이스케에 의해 독립적으로 개발되었고, 그들은 표준기수라고 이름 지었습니다. 일부 저자들은 이 용어를 그뢰브너 염기를 나타내기 위해 사용하기도 했습니다.

그뢰브너 기지의 이론은 많은 저자들에 의해 다양한 방향으로 확장되었습니다. 이는 주 이상환이나 다항식에 대한 다항식과 같은 다른 구조와 오레대수와 같은 비가환 고리와 대수의 일부 클래스로 일반화되었습니다.

도구들

다항식환

그뢰브너 기저는 주로 K 필드 위의 다항식 $링$ R = K${\displaystyle }$[ x$,$ …, x n ] {\displaystyle R = K [x_{1},\ldots,x_{n}}의 이상에 대해 정의됩니다. 이론은 모든 분야에서 효과가 있지만 대부분의 그뢰브너 기초 계산은 K가 유리수의 장이거나 정수 모듈로 소수일 때 수행됩니다.

그뢰브너 기저의 맥락에서, $R$ = ${\displaystyle K}$[ ${\displaystyle x_{}}$ $,$ …, x n ] {\displaystyle R = K[x_{1},\ldots,x_{n}}의 0이 아닌 다항식은 일반적으로 합 c $1$ M + ⋯ + c mm, {\displaystyle c_{1} M_{1}+\cdots + c_{m$}M_{m},}$ where the ${\displaystyle c_{i}}$ are nonzero elements of K, called coefficients, and the ${\displaystyle M_{i}}$ are monomials (called power products by Buchberger and some of his followers) of the form ${\displaystyle x_{1}^{a_{1}}\cdots x_{n}^{a_{n}},$$}$여기서$$ ${\displaystyle {ai}_{}}$ ${\$는 음이 아닌 정수입니다. 벡터 $A$ =${\displaystyle }$[${\displaystyle {}_{}}$ $,$ …, n] {\displaystyle A = [a_{1},\ldots,a_{n}}를 다항식의 지수 벡터라고 합니다. 변수 중 $X$ =${\displaystyle }$[ x $,$ …, ${\displaystyle {{}_{}}_{}^{}}$ n ] $displaystyle$ X = [x_{1},\ldots,x_{n}} 목록이 고정된 경우, 단항 표기법은 종종 x 1 a 1 ⋯ x n n = X A로 약칭됩니다. {\displaystyle x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}= X^{A}.$}$

단항식은 그들의 지수 벡터에 의해 고유하게 정의되며, 단항식 순서(아래 참조)가 고정되면, 다항식은 지수 벡터와 해당 계수에 의해 형성된 순서 쌍의 순서화된 목록에 의해 고유하게 표현됩니다. 다항식의 이러한 표현은 다항식 인수분해 및 다항식 최대 공약수와 같은 다른 계산에는 덜 편리하지만 컴퓨터에서 그뢰브너 기저 계산에 특히 효율적입니다.

$F$ =${\displaystyle }${ ${\displaystyle {}_{}}$ $,$ $…,$ f k} {\displaystyle F =\{f_{1},\ldots,$f_{k}\}$는 다항식 링 R의 유한 다항식 집합이며, F에 의해 생성된 이상은 $\underset{}{\overset{}{F}}$의 원소들의 선형 조합의 집합이며, 만약 i가 {\textstyle \sum_{${\displaystyle i}$$=$1}^{k}g_{i}f_{i}가 g, ${\displaystyle \dots ,}$ g k $∈$ R인 $경우$ $∑$ $i_{}$ $=$ ${}_{}$ $k_{}$ g라고 쓸 수 있는 다항식 집합입니다.${\displaystyle g_{1},\ldots,g_{k}\in R.}$

단항순서

그뢰브너 기저와 관련된 모든 연산은 다음과 같은 성질의 곱셈과의 호환성을 갖는 단항에 대한 전체 차수의 선택을 필요로 합니다. 모든 다항식 M, N, P에 대하여,

1. ${\displaystyle M\leq N\Long leftright 화살표 MP\leq NP}$
2. ${\displaystyle M\le }$ ${\displaystyle \mathrm{MP}}$ ${\displaystyle$ M$\leq MP}$입니다$.$

이러한 조건을 만족하는 전체 주문을 허용 주문이라고도 합니다.

이러한 조건들은 순서가 잘 정렬되어 있다는 것을 의미합니다. 즉, 모든 엄격하게 감소하는 일련의 단항들은 유한합니다.

그뢰브너 기저 이론은 허용되는 단항 순서의 특정 선택에 의존하지 않지만, 세 가지 단항 순서는 응용에 특히 중요합니다.

• 사전적 순서, 일반적으로 lex 또는 plex(순수 어휘 순서)라고 하는 사전적 순서입니다.
• 일반적으로 역순 사전순서 순서, 일반적으로 역순서 순서입니다.
• 제거 명령, 렉스데그.

그뢰브너 기저 이론은 처음에 사전적 순서를 위해 도입되었습니다. 그뢰브너 기저는 디그레블렉스를 계산하는 것이 거의 항상 훨씬 더 쉽다는 것과, 디그레블렉스 기저를 먼저 계산한 다음 "순서 변경 알고리즘"을 사용하여 렉스 그뢰브너 기저를 계산하는 것이 거의 항상 더 쉽다는 것을 곧 깨달았습니다. 제거가 필요할 때는 degrelex가 편리하지 않습니다. 렉스와 렉스데그를 모두 사용할 수도 있지만, 렉스데그에서는 비교적 쉽고 렉스에서는 거의 불가능합니다.

기본작업

선행항, 계수 및 단항

다항식의 순서가 고정되면 다항식(계수가 0이 아닌 다항식의 곱)의 항은 (이 순서에 대해) 감소함으로써 자연스럽게 순서가 정해집니다. 이것은 정렬된 쌍 계수-지수 벡터 목록으로서의 다항식의 표현을 다항식의 표준 표현(즉, 동일한 표현을 갖는 경우에만 두 다항식이 동일함)으로 만듭니다.

이 순서에 대한 다항식 p의 첫 번째(가장 큰) 항과 이에 해당하는 다항식 및 계수를 각각 선행 항, 선행 다항식 및 선행 계수라고 하며 이 문서에서는 lt(p), lm(p) 및 lc(p)로 표시합니다.

그뢰브너 기저와 관련된 대부분의 다항식 연산은 선두 항을 포함합니다. 따라서 다항식을 정렬된 목록으로 표현하면 이러한 연산이 특히 효율적입니다(목록의 첫 번째 요소를 읽는 데는 목록의 길이와 무관하게 일정한 시간이 소요됩니다).

다항식 연산

그뢰브너 기저 계산과 관련된 다른 다항식 연산들도 다항식 순서와 호환됩니다. 즉, 결과를 순서 변경하지 않고 수행할 수 있습니다.

• 두 다항식의 추가는 두 개의 대응하는 항 목록의 병합으로 구성되며, 충돌의 경우(즉, 두 다항식에서 동일한 단항식이 나타나는 경우) 특별한 처리가 있습니다.
• 다항식에 스칼라를 곱하는 것은 표현의 다른 변화 없이 각 계수에 이 스칼라를 곱하는 것으로 구성됩니다.
• 다항식에 m을 곱하는 것은 다항식의 각 다항식에 m을 곱하는 것으로 구성됩니다. 단항 순서화의 정의에 따라 순서화라는 용어가 변경되는 것은 아닙니다.

화폐의 가분성

Let ${\displaystyle M=x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}}$ and ${\displaystyle N=x_{1}^{b_{1}}\cdots x_{n}^{b_{n}}}$ be two monomials, with exponent vectors ${\displaystyle A=[a_{1},\ldots ,$$a_{n}}$ 및 $B$ $=$${\displaystyle }$[${\displaystyle {}_{}}$1, …, b$n]$ . {\displaystyle B $=$ [b_{1},\ldots,b_{n}].$}$

어떤 사람은 M이 N을 나누거나, $만약{\displaystyle {}_{}}$ ${\displaystyle a_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {b이면}_{}}$ 모든 i에 대해$$ ${\$ 즉 A가 성분적으로 B보다 크지 않으면 N은 M의 배수라고 말합니다. 이 경우, $몫$ $\frac{\mathrm{NM}}{}${\$textstyle${\$frac {N}{M}}$은 $\frac{\mathrm{NM}}{}$ = $x_{}^{}$ ${}_{}^{}$ b${1_{}}_{}^{}$ - ${{}_{}}_{}^{}$ ${1_{}}_{}^{}$⋯ x n b n - n으로 정의됩니다. {\textstyle {\frac {N}{M}}=x_{1}^{b_{1}-a_{1}}\cdots x_{n}^{b_{n}-a_{n}}. 즉, $\frac{\mathrm{NM}}{}$ ${\$의 지수 벡터는 N과 M의 지수 벡터의 성분별 감산입니다$$.

M과 N의 최대 공약수 gcd(${{}_{}}_{}^{}$, N)는 단항 $x$ ${1분}_{}^{}$(a 1${{}_{}}_{}^{}$ ${{}_{}}_{}^{}$ $1_{}^{}{{}_{}}_{}^{}$⋯${}_{}^{}$x ${{n분}_{}{n}_{}}_{}^{}$, $b$ n) ${\textstyle x_{1}^{\min(a_{$1}, b_{$1)}\cdots x_{n}^{\min(a_{$n}, b_{n)}}이며, 지수 벡터는 A와 B의 성분별 최소값입니다. 최소 공배수 lcm(M, N)은 min 대신 max로 유사하게 정의됩니다.

하나는.

${\displaystyle \operatorname {lcm}(M,N)={\frac {MN}{\gcd(M,N)}}.$

축소

단항 순서에 대한 다른 다항식에 의한 다항식의 감소는 그뢰브너 기저 이론의 중심입니다. 이는 일변량 다항식의 유클리드 분할의 가우스 제거 및 분할 단계에서 발생하는 행 감소의 일반화입니다.^[1] 가능한 한 많이 완성하면 결과가 고유하게 정의되지는 않지만 다변량 나눗셈이라고도 합니다.

납-환원은 계산이 더 쉬운 특수한 환원 사례입니다. 그뢰브너 기반 계산이 끝날 때만 일반적인 감소가 필요하기 때문에 비감소로부터 감소된 그뢰브너 기반을 얻기 위해 그뢰브너 기반 계산에 기본적입니다.

이 절에서 발생할 모든 단항 비교를 참조하는 허용되는 단항 순서를 고정합니다.

선행 다항식 lm(f)가 lm(g)의 배수일 경우 다항식 f는 다른 다항식 g에 의해 리드-리듀싱 가능합니다. 다항식 f는 f 의 어떤 다항식이 lm(g)의 배수이면 g만큼 줄일 수 있습니다. (따라서 f가 g만큼 납을 환원시킬 수 있는 경우 역시 환원이 가능하지만, f는 납을 환원시키지 않고 환원시킬 수 있습니다.)

f를 g만큼 줄일 수 있다고 가정하고, cm를 m이 lm(g)의 배수가 되도록 off 항이라고 가정합니다. f를 g만큼 한 단계 줄이는 것은 f를 다음과 같이 대체하는 것으로 구성됩니다.

${\displaystyle \operatorname {red}_{1}(f,g)=f-{\frac {c}{\operatorname {lc}(g)}\,{\frac {m}{\operatorname {lm}(g)}\,g.}$

이 작업은 m보다 큰 단항(단항 순서의 경우)으로 항을 변경하지 않고 f에서 단항 m을 제거합니다. 특히 f의 1단계 리드 리듀스는 모든 단항이 lm(f)보다 작은 다항식을 생성합니다.

다항식들의 유한 집합 G가 주어졌을 때, f가 G의 적어도 한 원소 g만큼 각각 환원성 또는 납 환원성이라면 G에 의해 환원성 또는 납 환원성이라고 말합니다. 이 경우, G에 의한 1단계 감소(resp. 1단계 리드-감소)는 G의 요소에 의한 오프의 1단계 감소(resp. 1단계 리드-감소)입니다.

(완전) 축소(resp). G에 의한 납-환원은 한 단계 환원(존경)을 반복하는 것으로 구성됩니다. 축소할 수 없는 다항식(resp)을 얻을 때까지 1단계 리드 축소). 납을 환원할 수 없음)에 의한 G 그것은 때때로 G에 의해 정상적인 형태의 off라고 불립니다. 일반적으로 이 형식은 일반적으로 f를 줄이는 데 사용될 수 있는 G의 여러 요소가 있기 때문에 유일하게 정의되지 않습니다. 이 비일관성은 그뢰브너 기저 이론의 출발점입니다.

축소의 정의는 그가 G에 의해 정상적인 형태의 f이면, 다음을 갖는다는 것을 즉시 보여줍니다.

${\displaystyle f=h+\sum _{g\in G}q_{g}\,g,}$

여기서 h는 G로 줄일 수 없고 ${\displaystyle {qg}_{}}$ ${\displaystyle q_{g}}$는 ${\displaystyle lm}$ ⁡ $q$ ${\displaystyle g)}$≤${\displaystyle \mathrm{lm}}$ ⁡ (f )와 같은 다항식입니다. {\$displaystyle \operatorname {lm}$ (q_{g}\,g)\leq$\operatorname$ {lm} (f)입니다.$}$일변량 다항식의 경우$$, G가 하나의 원소 g로 구성되어 있다면, h는 f의 나머지를 g로 나눈 유클리드의 나머지이고, q는_g 몫입니다. 게다가 분할 알고리즘은 정확히 납 환원의 과정입니다. 이 때문에 일부 저자는 축소 대신 다변량 분할이라는 용어를 사용합니다.

축소의 유일성이 없음

다음 예제에서는 두 개의 매우 다른 결과를 생성하는 완전한 납 감소가 정확히 두 개 있습니다. 결과가 환원 불가능(납 환원 불가능할 뿐만 아니라)하다는 사실은 이러한 작은 예에서 다소 일반적이지만 예제에 따라 다릅니다.

이 두 가지 변수 예제에서 사용된 단항 는x >$,$ {\$display$x>$y,}$를 사용한 사전 순서이며, 다음의 감소를 고려합니다.

$G$ =${\displaystyle }${${\displaystyle {}_{}}$1, g 2}, {\displaystyle G=\{g_{1}, g_{2}\}에 따라

제1 저감 단계의 경우, 제1 또는 제2 기간(f) 중 어느 하나가 저감될 수 있습니다. 그러나 한 용어의 축소는 새로운 하위 용어를 추가하는 비용으로 이 용어를 제거하는 것에 해당합니다. 첫 번째 축소 가능한 용어가 아닌 경우에는 추가 축소를 통해 유사한 용어를 추가하는 경우가 발생할 수 있으며, 이는 다시 축소되어야 합니다. 따라서 가장 큰 (단항 차수의 경우) 환원 가능 항을 먼저 줄이는 것이 더 좋습니다. 즉, 납 환원 불가능 다항식을 얻을 때까지 먼저 납 환원을 하는 것이 더 좋습니다.

f의 선행항 $2{\displaystyle \mathrm{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ ${\$은 $g{\displaystyle {}_{}}$ $1{\displaystyle {}_{}}$ ${\$만큼 감소할 수 있고$$${\displaystyle {}_{}{g\mathrm{}}_{}}$ 2만큼 감소할 수 없습니다$.$ {\$displaystyle g_{$2$$}}. 따라서 첫 번째 $감소{\displaystyle {}_{}}$ ${\displaystyle {단계}_{}}$는$$g 1 {\$displaystyle g_{1}}$에 –2x를 곱하고 결과를 f에 추가하는 것으로 구성됩니다.

${\displaystyle f\;{\overset {-2xg_{1}}{\longrightarrow }}\;f_{1}=f-2xg_{1}=-x^{2}y-2xy^{2}+2x+y^{3}+3y.}$

$f{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$의 선행 항${\displaystyle }$- x ${\displaystyle {}^{}}$ ${\displaystyle {y\mathrm{}}^{}}$ ${\displaystyle -x^{2}y}$는 ${\displaystyle {g\mathrm{}}_{}}$ 1 ${\$ 및 ${\displaystyle g_{}}$ $2{\displaystyle {}_{}}$ ${\displaystyle g_{2}$의 선행 항의 배수입니다. 따라서$$ 두 번째 축소 단계에는 두 가지 선택 사항이 있습니다. ${\displaystyle {g2\mathrm{}}_{}}$ ${\displaystyle g_{2}}$을(를) 선택하면 ${\displaystyle {g2만큼\mathrm{}}_{}}$ 다시 줄일 수 있는 다항식을${\displaystyle {}_{}}$얻습니다$$$.$ {\$displaystyle g_{2$}\colon $}$

${\displaystyle f\;{\overset {-2xg_{1}}{\longrightarrow }}\;f_{1}\;{\overset {xg_{2}}{\longrightarrow }}\;-2xy^{2}+y^{3}+3y\;{\overset {2yg_{2}}{\longrightarrow }}\;f_{2}=y^{3}-y.}$

더 이상의 축소는 불가능하므로 2 ${\$는 f의 완전한 축소입니다$$.

하나는 두 번째 단계에 대한 다른 선택으로 다른 결과를 얻습니다.

${\displaystyle f\;{\overset {-2xg_{1}}{\longrightarrow }}\;f_{1}\;{\overset {yg_{1}}{\longrightarrow }}\;-2xy^{2}+2x+2y^{3}+2y\;{\overset {2yg_{2}}{\longrightarrow }}\;f_{3}=2x+2y^{3}-2y.}$

다시 말하지만, 납 ${\displaystyle {감소}_{}}$만 이루어졌지만 3 ${\$의 결과는 줄일 수 없습니다$$.

요약하면 f의 완전한 감소는 ${\displaystyle f_{}}$ 2 = ${\displaystyle y}$ ${\displaystyle 3^{}}$- y $displaystyle f_{2$} = y^{$3}-y}$ 또는 f 3 = 2 x + 2 y 3 - 2 y. {\displaystyle f_{3} = 2x+2y^{3}-2y.}를 발생시킬 수 있습니다.

부흐베르거가 그뢰브너 기저와 S-다항체를 도입한 것은 이 비특이성이 설정한 문제를 다루기 위한 것입니다. 직관적으로 0 = f - f는 ${\displaystyle f_{}}$ $2{\displaystyle {}_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle 3_{}}$으로 감소될 수 있습니다${\displaystyle {}_{}}$ ${\displaystyle f_{2}-f_{3}}$ ${\displaystyle {이}_{}}$는 $f$ 2${\displaystyle {}_{}}$- f ${\displaystyle 3_{}}$ ${\displaystyle f_{2}-f_{3}}$가 G에 의해 생성된 이상에 속함을 의미합니다. 따라서, $이$ 이상은 G에 f ${\displaystyle 3_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle 2_{}}${\$displaystyle f_{3}-f_{2}$를 추가해도 변경되지 않으며, 이는 더 많은 감소를 허용합니다. 특히, ${\displaystyle {f3\mathrm{}}_{}}$ ${\$는 ${\displaystyle {f3\mathrm{}}_{}}$- ${\displaystyle {f2\mathrm{}}_{}}$ ${\$만큼$$ $f2{\displaystyle {}_{}}$ ${\$로 축소될 수 있으며$$$$, 축소된 형태의 고유성을 회복합니다.

여기서 그뢰브너 기저에 대한 부흐베르거의 알고리즘은 G에 다항식을 더하는 것으로 시작할 것입니다.

${\displaystyle g_{3}=yg_{1}-xg_{2}=2x+y^{3}-y.}$

부흐베르거에 의해 S-다항식이라고 불리는 이 다항식은 ${\displaystyle g_{}}$ 1 ${\display g_{1}}$ 및 g ${\displaystyle 2_{}}$ ${\display g_{2}}$의 선행 다항식의 최소 공배수 $x$ 2 ${\displaystyle {}^{}}$ ${\display$ x$^{2}y}$의 한 단계 감소의 차이입니다(이 예에서 하나는 g ${\displaystyle 3_{}}$ = ${\displaystyle f_{}}$ 3${\displaystyle {}_{}}$- f ${\displaystyle {}_{}).}$${\displaystyle g_{3}=f_{3}-f_{2}).$$}$이것은$$ xy가 ${\displaystyle {g2\mathrm{}}_{}}$ ${\$ 또는$$ $.{\display g_{3}$만큼 감소했을 때 다른 결과를 제공하므로 Buchberger의 알고리즘을 완료하지 않습니다.$}$

S-polynomial

주어진 다항식 순서에 대하여 임계쌍이라고도 불리는 두 다항식 f와 g의 S-다항식은 다항식입니다.

${\displaystyle {\begin{aligned}S(f,g)&=\operatorname {red}_{1}(\mathrm {lcm},g)-\operatorname {red}_{1}(\mathrm {lcm},f)\&={\frac {1}{\operatorname {lc}(f)}(g)}\,{\frac {\operatorname {gcd}}(g)}\,f-{\frac {1}{\operatorname {lc}(g)}}\,{\frac {\operatorname {lm}(f)}{\mathrm {gcd}}}\,g,\end{aligned}}}$

여기서 lcm 및 gcd는 각각 f 및 g의 선두 단항의 최소 공배수 및 최대 공약수를 나타냅니다.

f와 g가 모두 축소할 수 있는 단항은 정확히 lcm의 배수이므로 S-다항만을 고려하여 축소의 유일하지 않은 모든 경우를 처리할 수 있습니다. 이는 그뢰브너 기저 이론과 이를 계산하기 위한 모든 알고리즘의 기본적인 사실입니다.

정의.

$R$ = ${\displaystyle F}$[ ${\displaystyle {}_{}}$1, …, x n ] {\displaystyle R = F[x_{1},\ldots,x_{n}}가 필드 F 위의 다항식 링이라고 하자. 이 절에서는 허용되는 일항 순서가 고정되었다고 가정합니다.

G를 이상 I을 생성하는 R의 유한 다항식 집합이라 하자. 집합 G는 (단항 순서화에 대한) 그뢰브너 기저, 더 정확하게는 I의 그뢰브너 기저입니다.

1. I의 다항식들의 선행 다항식들에 의해 생성된 이상은 G의 선행 다항식들에 의해 생성된 이상과 같습니다.

아니면, 동등하게,

많은 특징적인 성질들이 있는데, 이 성질들은 각각 그뢰브너 염기들의 동등한 정의로 간주될 수 있습니다. 예를 들어, 다음 목록에서 "한 단어/다른 단어"라는 표기법은 그뢰브너 염기의 두 가지 다른 특성을 갖는 것에 대해 "한 단어" 또는 "다른 단어"를 취할 수 있음을 의미합니다. 다음과 같은 주장은 모두 그뢰브너 기저의 특성입니다.

위의 정의를 세어 보면, 이것은 그뢰브너 염기의 12가지 특성을 제공합니다. 이렇게 많은 특성화가 가능하다는 사실은 그뢰브너 염기를 매우 유용하게 만듭니다. 예를들면, 조건 3은 이상적인 멤버쉽을 테스트하기 위한 알고리즘을 제공하고, 조건 4는 다항식들의 집합이 그뢰브너 기저인지를 테스트하기 위한 알고리즘을 제공하고, 그뢰브너 기저를 계산하기 위한 부흐베르거의 알고리즘의 기초를 형성하며, 조건 5 및 6은 모듈식과 매우 유사한 방식으로$$ $R{\displaystyle }$ /${\displaystyle I}$ ${\display R/I}$에서 컴퓨팅을 허용하는 것을 특징으로 하는 방법산수의

그뢰브너 기지의 존재. 모든 허용되는 다항식 순서와 다항식의 모든 유한 집합 G에 대하여, G를 포함하고 동일한 이상을 생성하는 그뢰브너 기저가 존재합니다. 또한, 그러한 그뢰브너 기저는 부흐베르거의 알고리즘으로 계산될 수 있습니다.

이 알고리즘은 조건 4를 사용하고, 대략 다음과 같이 진행합니다: G의 두 원소의 S-다항체의 G에 의한 완전한 감소의 0이 아닌 결과를 모두 G에 더합니다; 결국 모든 감소가 0을 생성할 때까지 G의 새로운 원소를 포함하여 이 연산을 반복합니다. 이 알고리즘은 항상 딕슨의 보조정리 때문에 또는 다항식 고리가 노에테리안(힐베르트의 기초 정리)이기 때문에 종결됩니다. 조건 4는 결과가 그뢰브너 기저임을 보장합니다.

그뢰브너 기지 축소

그뢰브너 기저는 그 원소의 모든 선행 단원이 기저의 다른 원소들에 의해 축소될 수 없는 경우 최소입니다. 이상 I의 그뢰브너 기저가 주어졌을 때, 선행 다항식이 그뢰브너 기저의 다른 원소의 선행 다항식의 배수인 다항식을 제거함으로써 최소 그뢰브너 기저 I을 얻게 됩니다. 그러나 기저의 두 다항식이 동일한 선행 다항식을 갖는 경우 하나만 제거해야 합니다. 따라서, 모든 그뢰브너 기저는 부분 집합으로 최소 그뢰브너 기저를 포함합니다.

주어진 이상의 모든 최소 그뢰브너 기저는 (고정된 단항 순서에 대해) 동일한 수의 원소를 가지며, 동일한 선두 단항을 가지며, 비최소 그뢰브너 기저는 최소보다 더 많은 원소를 갖습니다.

그뢰브너 기저는 그 안에 있는 모든 다항식이 기저의 다른 요소들에 의해 감소될 수 없고 1을 선행 계수로 가지는 경우 감소됩니다. 따라서, 모든 감소된 그뢰브너 기저는 최소이지만 최소 그뢰브너 기저는 감소될 필요가 없습니다.

이상 I의 그뢰브너 기저가 주어지면, 먼저 기저의 다른 원소에 의해 납 환원이 가능한 다항식을 제거하고, 그 기저의 각 원소를 다른 원소에 의한 완전한 환원의 결과로 대체함으로써 I의 환원된 그뢰브너 기저를 얻게 됩니다. 기초의 각 요소를 선행 계수로 나누는 방법.

(고정된 다항식 순서에 대하여) 이상의 모든 축소된 그뢰브너 기저는 같습니다. 따라서 두 개의 이상은 동일한 그뢰브너 기저를 갖는 경우에만 동일합니다.

때때로 선행 계수의 조건 없이 축소된 그뢰브너 기저가 정의되기도 합니다. 이 경우, 감소된 그뢰브너 기저의 유일성은 다항식의 0이 아닌 상수의 곱셈까지만 사실입니다.

유리수의 $Q{\displaystyle \mathbb{}}$ ${\$ 필드 위에서 다항식을 사용할 때는 정수 계수를 가진 다항식만 사용하는 것이 유용합니다. 이 경우, 감소된 기저의 정의에서 선도 계수에 대한 조건은 기저의 모든 요소가 정수 계수를 갖는 원시 다항식이고 양의 선도 계수를 갖는 조건으로 대체될 수 있습니다. 이렇게 하면 축소된 베이스의 고유성을 회복할 수 있습니다.

그뢰브너 기저 계산의 대부분의 구현에서 출력되는 그뢰브너 기저는 항상 감소됩니다.^{[citation needed]}

특수한 경우

모든 다항식의 순서에 대하여, 빈 다항식 집합은 영 아이디얼의 유일한 그뢰브너 기저입니다.

모든 다항식 순서에 대해 0이 아닌 상수를 포함하는 다항식 집합은 단위 이상(전체 다항식 링)의 그뢰브너 기저입니다. 반대로, 단위 아이디얼의 모든 그뢰브너 기저는 0이 아닌 상수를 포함합니다. 단위의 축소된 그뢰브너 기저는 단일 다항식 1에 의해 형성됩니다.

단일 변수의 다항식의 경우 고유하게 허용되는 다항식 순서, 즉 차수별 순서가 있습니다. 최소 그뢰브너 기저는 단일 다항식으로 구성된 단일 원뿔입니다. 축소된 그뢰브너 기저는 모닉 다항식입니다.

예제 및 반례

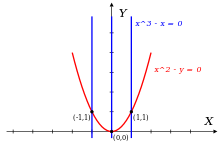
$R$ = ${\displaystyle Q}$[ $,$ y ] {\$displaystyle$ R =\mathbb {Q} [x,y]}를 유리 계수를 갖는 이변량 다항식의 환이라 하고 다항식으로 생성된 이상 I = ⟨ f, g ⟩ {\displaystyle I =\langle f, g\rangle }를 고려합니다.

${\displaystyle f}$ = ${\displaystyle {}^{}}$2 - y {\displaystyl${\displaystyle e}$ f = x^{2}-y},

${\displaystyle g}$ = ${\displaystyle {}^{}}$3 - x {\displaystyl${\displaystyle e}$ g = x^{3}-x}.

g를 f만큼 줄이면 ${\displaystyle I}$ = ⟨${\displaystyle }$f$,$k ⟩ : {\displaystyle I=\langle f, k\rangle :}와 같은 새로운 다항식 k를 얻을 수 있습니다.

${\displaystyle k=g-xf=xy-x.}$

f와 k 중 어느 것도 다른 것에 의해 축소될 수 없지만, xk는 f에 의해 축소될 수 있으며, 이는 I에서 또 다른 다항식을 제공합니다.

${\displaystyle h=xk-(y-1)f=y^{2}-y.}$

> ${\displaystyle x>y}$를 사용한 사전 순서 아래에 있습니다.

lt(f) = x

lt(k) = xy

lt(h) = y

f, k 및 h는 I에 속하며, 그 중 어느 것도 다른 것에 의해 축소될 수 없습니다$.{\displaystyle }$ {${\displaystyle f,}$ k${\displaystyle \},}$ ${\displaystyle \{$${\displaystyle f}$$, k$${\displaystyle \{f,$ h$\},$${\displaystyle }${${\displaystyle h,}$ ${\displaystyle k\}}$ ${\displaystyle \{h,$ k$\}$ 중$$ 어느 것도 I의 그뢰브너 기저입니다$$.

반면, {f, k, h}는 S-다항식이므로 I의 그뢰브너 기저입니다.

${\displaystyle {\begin{aligned}yf-xk&=y(x^{2}-y)-x(xy-x)=f-h\\yk-xh&=y(xy-x)-x(y^{2}-y)=0\\y^{2}f-x^{2}h&=y(yf-xk)+x(yk-xh)\end{aligned}}}$

f, k, h에 의해 0으로 감소할 수 있습니다.

여기서 h와 k를 찾고 {f, k, h}가 그뢰브너 기저임을 증명하는 데 사용된 방법은 부흐베르거의 알고리즘을 직접 적용한 것입니다. 따라서 일반적으로 고려해야 할 다항식과 S-다항식이 많고 컴퓨터 없이 계산하기에는 일반적으로 너무 큰 연산이지만 유사한 예에 기계적으로 적용할 수 있습니다.

그뢰브너 기지의 특성과 응용

명시적으로 언급하지 않는 한, 다음의^[3] 모든 결과는 모든 단항 주문에 대해 사실입니다(아래에 언급된 다양한 주문의 정의는 해당 문서를 참조하십시오).

이러한 결과 중 일부에는 사전 순서가 필요하다는 것이 일반적인 오해입니다. 반대로, 사전적 순서는 거의 항상 계산하기 가장 어려우며, 이를 사용하면 등급화된 역 사전적 순서(grevlex)로 비교적 쉬운 비현실적인 많은 계산이나 제거가 필요할 때 각 변수 블록에서 grevlex로 제한되는 제거 순서(lexdeg)를 만듭니다.

이상의 평등

축소된 그뢰브너 기저는 어떤 주어진 이상과 어떤 다항식 순서에 대해서도 고유합니다. 따라서 두 개의 이상은 동일한 그뢰브너 기저(보통 그뢰브너 기저 소프트웨어는 항상 감소된 그뢰브너 기저를 생성함)를 갖는 경우에만 동일합니다.

회원가입 및 이상의 포함

이상 I의 그뢰브너 기저 G에 의한 다항식 f의 감소는 f가 I에 있는 경우에만 0을 산출합니다. 이를 통해 이상적인 요소의 구성원 자격을 테스트할 수 있습니다. 또 다른 방법은 G ∪{f}의 그뢰브너 기저가 G와 같음을 확인하는 것입니다.

f, ..., f에 의해 생성된 이상 I가 이상 J에 포함되어 있는지를 검정하기 위해서는 모든 것이 J에 포함되어 있음을 검정하는 것으로 충분합니다. 또한 J와 ∪ {f, ...,f}의 그뢰브너 축소 기저의 동일성을 검정할 수도 있습니다.

대수 방정식 체계의 해

어떤 다항식 집합은 다항식을 0과 같게 함으로써 다항식의 체계로 볼 수 있습니다. 이러한 시스템의 솔루션 세트는 생성된 이상에만 의존하므로 주어진 생성 세트가 어떤 순서에 대해 생성된 이상의 그뢰브너 기저로 대체되어도 변하지 않습니다. 다항식의 계수를 포함하는 대수적으로 닫힌 장에 좌표가 있는 그러한 해를 이상의 0이라고 합니다. 일반적으로 유리 계수의 경우 이 대수적으로 닫힌 필드가 복소 필드로 선택됩니다.

1이 이상에 속하거나(이는 힐베르트의 널스텔렌사츠), 그뢰브너 기저가 1을 포함하거나, 대응하는 감소된 그뢰브너 기저가 [1]인 경우에만 이상은 0이 없습니다.

이상 I의 그뢰브너 기저 G가 주어졌을 때, 각 변수 x에 대해 G가 x의 거듭제곱인 선행 다항식을 포함하는 경우에만 유한한 수의 0을 갖습니다(선행 항에 나타나는 다른 변수는 없음). 그렇다면 다중성으로 계산한 0의 수는 G의 선행 단항의 배수가 아닌 단항의 수와 같습니다. 이 숫자를 이상의 정도라고 합니다.

0의 수가 유한할 때, 사전적 일항 순서에 대한 그뢰브너 기저는 이론적으로 다음과 같은 해를 제공합니다. 해의 첫 번째 좌표는 첫 번째 변수에만 의존하는 기저 다항식의 최대 공약수의 근입니다. 이 근을 기저에 대입한 후, 이 해의 두 번째 좌표는 두 번째 변수에만 의존하는 결과 다항식의 최대 공약수의 근 등입니다. 이 해결 과정은 GCD 계산과 대략적인 계수를 가진 다항식의 근 찾기를 의미하기 때문에, 숫자의 불안정성 때문에 실행할 수 없습니다. 따라서 그뢰브너 기저를 통해 다항식 시스템을 해결하기 위한 다른 방법이 개발되었습니다(자세한 내용은 다항식 시스템 참조).

차원, 차수 및 힐베르트 급수

다항식 환 R에서의 이상 I의 차원은 환 R/I의 크룰 차원이며, I의 0의 대수 집합의 차원과 같습니다. 또한 일반적인 위치에서 유한 개의 점인 대수 집합과 교집합을 갖는 데 필요한 초평면의 수와 같습니다. 이상과 관련 대수 집합의 정도는 다중으로 계산된 이 유한 교차점의 점 수이다. 특히 초표면의 정도는 정의 다항식의 정도와 같습니다.

정도와 차원은 모두 어떤 단항 순서에 대한 이상적인 그뢰브너 기저의 선행 단항들의 집합에만 의존합니다.

차원은 S의 변수에만 의존하는 선행 단항이 없도록 변수 부분 집합 S의 최대 크기입니다. 따라서, 이상이 차원 0을 가지면, 각 변수 x에 대하여 x의 거듭제곱인 그뢰브너 기저에 선행 단항식이 존재합니다.

차원과 정도는 이상의 힐베르트 $\underset{}{\overset{}{급수}}$에서 추론할 수 있는데, 이는 시리즈 ∑ $i_{}$ = $0$ ∞$di$ di {\textstyle \sum _{i=0}^{\infty }d_{i}t^{i}}입니다. 여기서 di {\displaystyle d_{i}}는 그뢰브너 기저에서 선도 단항의 배수가 아닌 i의 단항의 개수입니다. 힐베르트 급수는 유리분수로 요약될 수 있습니다.

${\displaystyle \sum _{i=0}^{\infty }d_{i}t^{i}={\frac {P(t)}{(1-t)^{d}}},}$

여기서 d는 아이디얼의 차원이고 $P{\displaystyle (t)}${\$displaystyle$P($t)}$는${\displaystyle }$P($)$ {\$displaystyle$P($1)}$가 아이디얼의 차수가 되는 다항식입니다.

차원과 정도는 다항식 순서의 선택에 의존하지 않지만, 힐베르트 급수와 $다항식{\displaystyle }$ P${\displaystyle (t)}$ ${\displaystyle$ P$(t)}$는 다항식 순서를 변경하면 바뀝니다$$.

그뢰브너 기저를 계산하는 함수를 제공하는 대부분의 컴퓨터 대수 시스템은 힐베르트 급수를 계산하는 함수도 제공하므로 차원과 정도도 제공합니다.

탈락

제거 다항식 순서화를 위한 그뢰브너 베이스의 계산은 계산 제거 이론을 허용합니다. 이것은 다음과 같은 정리에 기초하고 있습니다.

변수가 두 부분집합 X와 Y로 분할되는 $다항식환$ K${\displaystyle }$[${\displaystyle x_{}}$ 1${\displaystyle {}_{}\dots ,}$ ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 1_{}\dots ,}$ ${\displaystyle y_{}}$ m${\displaystyle {}_{}}$ = K${\displaystyle }$[$,$ Y], {\displaystyle K[x_{1},\ldots,x_{n},y_{1},\ldots,y_{m}] = K[X,Y]를 생각해 보자. 또한 제거 다항식 "제거" X를 선택할 수 있는데, 이것은 두 다항식을 먼저 X-부분을 비교하여 비교하는 것이며, Y-부분을 고려하여 동일한 경우에만 비교하는 다항식입니다. 이는 X-변수를 포함하는 단항식이 X와 무관한 모든 단항식보다 크다는 것을 의미합니다. 만약 ${\displaystyle G}$가 이 다항식 순서에 대한 아이디얼 I의 그뢰브너 기저라면, $G$ ∩ K$[Y$] {\$displaystyle G\$cap K[Y]}는 I ∩ K[Y] {\displaystyle I\cap K[Y]}의 그뢰브너 기저입니다(이 아이디얼은 종종 제거 아이디얼이라고 불립니다). ${\displaystyle \mathrm{또한}}$ G ∩ K$$[Y$]$ ${\displaystyle G\$cap K[Y]}는 선행 항이 K[Y]에 속하는 G의 다항식으로 정확히 구성됩니다(선행 단항만 확인하면 되므로 G ∩ K [Y] {\displaystyle G\cap K[Y]}의 계산이 매우 쉽습니다).

이 제거 속성에는 많은 응용 프로그램이 있으며 일부는 다음 섹션에서 설명합니다.

대수기하학에서 또 다른 응용은 제거가 주변 공간의 하위 공간으로의 아핀 대수 집합의 투영의 기하학적 연산을 실현한다는 것입니다. 위의 표기법으로 이상 I에 의해 정의된 대수 집합의 Y 하위 공간으로의 투영(자리스키 폐쇄)은 $이상$ ${\displaystyle I}$ ∩ K${\displaystyle [}$Y]에 의해 정의됩니다.${\displaystyle I\cap K[Y]$$입니다.$$}$

> ⋯ > x n {\$displaystyle x_${1}$>\cdots >$ x_{n}}와 같은 사전 순서는 모든${\displaystyle {파티션}_{}}${${\displaystyle x_{}}$1,${\displaystyle {}_{}\dots ,{}_{}}$ k + ${\displaystyle 1_{}{,}_{}}$…,${\displaystyle }$x$$n}에 대한 $제거$ 순서입니다. ${\displaystyle$\{$x_${1$},\ldots,$x_{$k}\},\{$x_{k+1$},\ldots,$x_{n}\}$$ 따라서 이 순서에 대한 그뢰브너 기반은 일반적으로 필요한 것보다 훨씬 더 많은 정보를 전달합니다. 이것은 그뢰브너의 사전 순서에 대한 기저가 일반적으로 계산하기 가장 어려운 이유를 설명할 수 있습니다.

교차하는 이상

I와 J가 각각 {f, ..., f} 및 {g, ..., g}에 의해 생성된 두 개의 이상일 경우, 단일 그뢰브너 기저 계산은 그들의 교집합 I ∩ J의 그뢰브너 기저를 생성합니다. 이를 위해, 새로운 불확정 t를 도입합니다. 첫 번째 블록은 t개만 포함하고 다른 블록은 다른 모든 변수를 포함하도록 제거 순서를 사용합니다(즉, t개를 포함하는 단항이 t개를 포함하지 않는 모든 단항보다 크다는 것을 의미합니다). 이 다항식의 순서에 따라, I ∩ J의 그뢰브너 기저는 이상의 그뢰브너 기저에 포함되지 않는 다항식들로 구성됩니다.

${\displaystyle K=\langle tf_{1},\ldots ,tf_{m},(1-t)g_{1},\ldots ,(1-t)g_{k}\rangle .}$

즉, I ∩ J는 K에서 t를 제거함으로써 얻어집니다. $이것은$∈ $I$ ${\$$style$ a$\$in I}와 b ∈ J {\display b\in J}인 다항식$$($a-b)t+b}$로 이루어진 이상 K의 구성이 증명될 수 있습니다. 이러한 다항식은 a=b인 경우에만 t와 무관하며, 이는 b ∈ I가 J ∩ {\style b\in I\cap J}임을 의미합니다.

유리 곡선의 암시화

유리 곡선은 다음과 같은 형태의 모수 방정식들의 집합을 갖는 대수적 곡선입니다.

${\displaystyle {\begin{aligned}x_{1}&={\frac {f_{1}(t)}{g_{1}(t)}}\\&\;\;\vdots \\x_{n}&={\frac {f_{n}(t)}{g_{n}(t)}},\end{aligned}}}$

$여기$서 ${\displaystyle {fi}_{}}$(${\displaystyle t)}$ ${\displaystyle f_{i}(t)}$ 및$$ ${\displaystyle {gi}_{}}$(${\displaystyle t)}$ ${\displaystyle g_{i}(t)}$는 1 ≤ i ≤ n에 대한 일변량 다항식입니다. ${\displaystyle {fi}_{}}$(${\displaystyle t)}$ ${\displaystyle f_{i}(t)}$ 및 ${\displaystyle {gi}_{}}$ ${\displaystyle {}_{}t)}$ ${\displaystyle g_{i}(t)}$가 공집합이라고 가정할 수 있습니다(이들은 일정하지 않은 공통 인자가 없습니다).

암시화는 그러한 곡선의 암시 방정식을 계산하는 것으로 구성됩니다. n = 2인 경우, 즉 평면 곡선의 경우, 이는 결과와 함께 계산될 수 있습니다. 암묵적 방정식은 다음과 같은 결과입니다.

${\displaystyle {\text{Res}}_{t}(g_{1}x_{1}-f_{1},g_{2}x_{2}-f_{2}).}$

그뢰브너 베이스를 사용하여 제거하면 ${\displaystyle {이상적}_{}}$인 ⟨${\displaystyle {}_{}}$g ${\displaystyle {}_{}}$ ${\displaystyle x_{}}$ 1${\displaystyle }$-${\displaystyle }$f ${\displaystyle 1_{}}$, …,${\displaystyle g_{}}$ ${\displaystyle n_{}}$ x${\displaystyle {}_{}}$n${\displaystyle }$-$$f n ⟩에서 t를 제거하는 것만으로 어떤 n 값에 대해서도 암시할 수 있습니다. {\$displaystyle \$lang$le$ g_{1$}x_{1}-f_{1},\ldots,g_${n$}$x_{n}-f_{n}\rangle .} n = 2인 경우 결과는 ${\displaystyle {맵}_{}}$ t가 ↦하면${\displaystyle {}_{}}$와 동일합니다${\displaystyle {}_{}}$ (x 1,)${\displaystyle x_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle t\mapsto (x_{1},x_{2})}$는 거의 모든 t에 대해 주입식입니다. 다른 경우에는, 그 결과는 탈락의 결과의 힘입니다.

채도

다항식으로 문제를 모델링할 때 퇴화된 경우를 피하기 위해 일부 양은 0이 아니라고 가정하는 경우가 많습니다. 예를 들어, 삼각형을 다룰 때 삼각형이 선분으로 전락하면 많은 특성이 거짓이 됩니다. 즉, 한 변의 길이는 다른 변의 길이의 합과 같습니다. 이러한 상황에서는 축퇴해를 무시하지 않는 한 다항식 시스템에서 관련 정보를 추론할 수 없습니다. 더 정확하게, 방정식 체계는 축소할 수 없는 여러 구성 요소를 가질 수 있는 대수 집합을 정의하고, 퇴행 조건이 0인 구성 요소를 어디에서나 제거해야 합니다.

이는 축퇴 조건에 의해 방정식을 포화시킴으로써 수행되며, 이는 그뢰브너 염기의 제거 특성을 통해 수행될 수 있습니다.

채도의 정의

고리의 위치는 일부 요소의 형식적인 역으로 인접해 있습니다. 이 절에서는 단일 원소 또는 이와 동등하게 유한한 수의 원소(여러 원소의 역수를 인접시키는 것은 그들의 곱의 역수를 인접시키는 것과 동일함)의 경우만을 다룹니다. 요소 f에 의한 링 R의 국소화는 링 $R$ ${\displaystyle f_{}}$ = ${\displaystyle R}$[ t${\displaystyle }$]$$/ (1 - ft ), {\displaystyle R_{f} = R[t] / (1 - ft), 여기서 t는 f의 역을 나타내는 새로운 불확정입니다. R의 이상 I의 국소화는 이상적인 ${\displaystyle {Rf}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle R_{f}$입니다.${\displaystyle {If}_{}}$. ${\displaystyle I_{f}$의 $I}.$ R이 다항식 ${\displaystyle {링일}_{}}$ 때, $Rf$ {\$displaystyle$ R_${f}$의 계산은 분모를 관리해야 하기 때문에 효율적이지 않습니다$$$.$ 따라서 일반적으로 로컬라이제이션은 포화 상태의 작동으로 대체됩니다.

R에서 이상 I의 f에 대한 채도는 ${\displaystyle {}_{}}$I {\$display R_{$f}의 역상입니다.R에서 R ${\displaystyle f_{}}$로의 표준 맵 $아래$의 I${\displaystyle {}_{}}$ ${\display R_{f}}$ 이것은 이상적인 $I{\displaystyle :f{}^{}}$$∞$ $=$ {${\displaystyle g}$$∈$${\displaystyle {}^{}}$ $∣$$($$∃$ $k$ $∈$ N) fk g $∈$ I} {\displaystyle I:f^{\infty} $=$\{g\in R\mid(\$exists$ k\in \mathbb {N})f^{k}g\in I\}이다. f 의 거듭제곱이 어느 정도인 곱이 I에 속하는 R의 모든 원소로 구성된다.

만약 J가 R[t]에서 I와 1-ft에 의해 생성된 아이디얼이라면, $I{\displaystyle :f{}^{}}$∞ ${\displaystyle }$= $J$∩ R. {\$displaystyle$ I:f^{\infty} =J\cap R.} R이 다항식 링일 경우, t를 제거하는 그뢰브너 기저 계산은 다항식에 의한 아이디얼의 포화에 대한 그뢰브너 기저를 생성합니다.

포화의 중요한 성질은 다항식 f가 0인 환원 불가능한 성분을 이상 I에 의해 정의된 대수 집합에서 제거하는 것을 보장합니다. $I$ ∞의 1차 $분해$ {\$displaystyle$ I$:$f^{\infty }}는 전원 오프를 포함하지 않는 I의 1차 분해 성분으로 구성됩니다.

채도 계산

$유한$ 집합의 다항식 F에 의해 생성된 다항식 이상의 포화 f에 의한 그뢰브너 기저는 ${\displaystyle F}$ ∪ {${\displaystyle 1}$-$$t f}, ${\displaystyle$F\$cup$\{1 - tf\}에서 t를 제거함으로써 구할 수 있습니다.$}$그것은 제거 순서 제거 t에 대하여 ${\displaystyle F}$ $∪$ {${\displaystyle 1}$- t $f$} ${\displaystyle$F\$cup$\{1 - tf\}의 그뢰브너 기저에서 다항식들을 t와 독립적으로 유지함으로써입니다.

F를 사용하는 대신 F의 그뢰브너 기저에서 시작할 수도 있습니다. 어떤 방법이 가장 효율적인지는 문제에 따라 다릅니다. 그러나 포화 상태에서 어떤 성분도 제거되지 않는다면, 즉 이상이 포화 상태의 이상과 같은 경우 F의 그뢰브너 기저를 먼저 계산하는 것이 일반적으로 더 빠릅니다. 반면 포화 상태가 일부 구성 요소를 제거하면 직접 계산 속도가 획기적으로 빨라질 수 있습니다.

여러 다항식 ${\displaystyle f_{}}$ 1${\displaystyle {}_{}}$ ${\displaystyle \dots ,{}_{}}$ ${\displaystyle k_{}}$ ${\displaystyle f_{1},\ldots, f_{k}$ 또는 곱 $f$ = ${\displaystyle f_{}}$ $1$⋯ f k, {\displaystyle f=f_{1}\cdots f_{k}에 대해 포화를 원하는 경우$}$동일한 결과를 제공하지만 계산 시간이 매우 다를 수 있는 세 가지 방법이 있습니다$$(어떤 것이 가장 효율적인지는 문제에 따라 다릅니다).

• 단일 그뢰브너 기반 계산에서 $f$ = ${\displaystyle {}_{}}$ $1$⋯ f k {\displaystyle f = f_{1}\cdots f_{k}}로 포화.
• $f{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle f_{1}}$만큼 포화한 다음$$ 결과를 $f{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle f_{2}$ 등으로$$ 포화시킵니다.
• 그뢰브너 기저에 다항식 $1{\displaystyle \mathrm{}}$- t ${\displaystyle {}_{}}$ ${\displaystyle {f\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}\dots ,}$ ${\displaystyle 1}$- ${\displaystyle t_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle f_{}}$ k${\displaystyle {}_{}}$ ${\displaystyle 1-t_{1}f_{1},\ldots, 1-t_{k}f_{k}}$를 추가하고$$ 단일 그뢰브너 기저 계산에서$$ ${\displaystyle {ti}_{}}$ ${\$를 제거합니다.

유효 널스텔렌사츠

힐베르트의 널스텔렌사츠에는 두 가지 버전이 있습니다. 첫 번째는 1이 생성된 이상에 속하는 경우에만 계수 필드의 대수적 폐쇄에 대해 다항식 집합에 공통 0이 없다고 주장합니다. 이것은 그뢰브너 기반 계산으로 쉽게 테스트됩니다. 왜냐하면 1이 이상의 그뢰브너 기반에 속하는 경우에만 1이 이상에 속하기 때문입니다.

두 번째 버전은 (계수 필드의 대수적 폐쇄에서) 이상의 공통 0들의 집합이 (f의 거듭제곱이 이상에 속하는 경우에만) 다항식 f의 0들의 초표면에 포함된다고 주장합니다. 이것은 f에 의해 이상을 포화시킴으로써 테스트될 수 있습니다. 사실 f에 의한 포화가 1을 포함하는 그뢰브너 기저를 제공하는 경우에만 power off가 이상에 속합니다.

높은 차원에서의 암시화

정의에 따라, 아핀 유리 다양한 차원 k는 다음과 같은 형태의 모수 방정식에 의해 기술될 수 있습니다.

${\displaystyle {\begin{aligned}x_{1}&={\frac {p_{1}}{p_{0}}\&\;\vdots \\x_{n}&={\frac {p_{n}}{p_{0}}\end{aligned}}}$

여기서 $p{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}\dots ,}$ ${\displaystyle p_{}}$ ${\$는 k개 변수(파라미터화의 파라미터) $t{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$…, ${\displaystyle t_{}}$ ${\displaystyle t_{1},\ldots, t_{k}$의 n+1 다항식입니다.$}$${\displaystyle {따라서}_{}}$ $변수$의 점의 ${\displaystyle {}_{}}$ 변수 t ${\displaystyle {1\mathrm{}}_{}\dots ,}$ t ${\$ 및 좌표$$ ${\displaystyle {x\mathrm{}}_{}}$ 1${\displaystyle {}_{}\dots ,}$ x ${\displaystyle n_{}}$ ${\$는 이상의 0입니다.

${\displaystyle I=\left\langle p_{0}x_{1}-p_{1},\ldots ,p_{0}x_{n}-p_{n}\right\rangle .}$

곡선의 경우와 마찬가지로 변수를 제거하면 다양성의 암묵적 방정식을 얻을 수 있습니다. 안타깝게도 항상 그렇지는 않습니다. $만약{\displaystyle {}_{}}$ ${\displaystyle {pi}_{}}$ ${\$가 공통의 0(때로는 기저점이라고도 함)을$$ 가지면, ${\displaystyle {pi}_{}}$ ${\$에 의해 정의된 비어 있지 않은 대수 집합의 모든 축소 불가능한 성분은 I에 의해 정의된 대수 집합의 축소 불가능한 성분입니다$$. 이 경우 ${\displaystyle t_{}}$ ${\$를 직접 제거하면 공다항식 집합이 제공됩니다$$.

따라서 k>1인 경우 다음을 암시하기 위해 두 개의 그뢰브너 기반 계산이 필요합니다.

1. $I{\displaystyle {}_{}}$ ${\$$displaystyle I}$을(를) p ${\displaystyle {0\mathrm{}}_{}}$ {\$displaystyle$ p_${0}$으로 포화시켜$$ 그뢰브너 $기저{\displaystyle }$ G ${\displaystyle$ G$}$을(를) 얻습니다.
2. $G{\displaystyle }$ ${\displaystyle G}$에서 ${\displaystyle {ti}_{}}$ ${\$를 제거하면$$ 다양성의 (묵시 방정식의) 이상적인 그뢰브너 기초를 얻을 수 있습니다.

알고리즘 및 구현

부흐베르거의 알고리즘은 그뢰브너 기저를 계산하는 가장 오래된 알고리즘입니다. 브루노 부흐베르거가 그뢰브너 기저 이론과 함께 고안한 것입니다. 구현하기는 간단하지만, 원시적인 구현은 사소한 문제들만 해결할 수 있다는 것이 곧 나타났습니다. 주요 문제는 다음과 같습니다.

1. 그뢰브너 기저가 작아도 중간 다항식은 엄청날 수 있습니다. 결과적으로 컴퓨팅 시간의 대부분은 메모리 관리에 사용될 수 있습니다. 따라서, 특화된 메모리 관리 알고리즘은 효율적인 구현의 기본적인 부분일 수 있습니다.
2. 계산 중에 발생하는 정수는 빠른 곱셈 알고리즘과 다중 모듈 산술을 유용하게 만들기에 충분히 클 수 있습니다. 이러한 이유로 대부분의 최적화된 구현은 GMP 라이브러리를 사용합니다. 또한, 모듈식 산술, 중국의 나머지 정리 및 헨젤 리프팅이 최적화된 구현에 사용됩니다.
3. 감소시키는 S-다항식과 이를 감소시키는 데 사용되는 다항식의 선택은 휴리스틱에 집중됩니다. 많은 계산 문제에서와 마찬가지로 휴리스틱은 대부분의 숨겨진 단순화를 감지할 수 없으며 휴리스틱 선택을 피할 경우 알고리즘 효율성이 극적으로 향상될 수 있습니다.
4. 대부분의 경우 계산되는 대부분의 S-다항은 0으로 줄어듭니다. 즉, 대부분의 계산 시간은 0을 계산하는 데 사용됩니다.
5. 응용 프로그램(순수 사전 기록)에 가장 자주 필요한 단항 순서는 가장 쉬운 계산, 일반적으로 순서 역순으로 이어지는 순서가 아닙니다.

3. 많은 개선 사항을 해결하기 위해 장 샤를 포제르(Jean-Charles Faugère)에 의해 F4 및 F5 알고리즘이 도입되기 전에 변형 및 휴리스틱이 제안되었습니다. 이러한 알고리즘은 정수 계수 또는 정수 모듈로 소수의 계수에 대해 설계되었기 때문에 부흐베르거의 알고리즘은 더 일반적인 계수에 유용하게 사용됩니다.

대략적으로, F4 알고리즘은 선형 대수의 고급 방법을 사용할 수 있는 단일 큰 행렬의 행 감소로 많은 S-다항 감소를 대체함으로써 3.를 해결합니다. 이는 부흐베르거 알고리즘에서 0으로의 축소는 축소될 행렬의 행 사이의 관계에 해당하고, 축소된 행렬의 0행은 이러한 관계의 벡터 공간의 기초에 해당하기 때문에 부분적으로 문제 4를 해결합니다.

F5 알고리즘은 행렬의 크기를 줄일 수 있는 기준을 도입하여 F4를 향상시킵니다. 이 기준은 감소할 행렬이 충분히 정규적인 경우(특히 입력 다항식이 정규 시퀀스를 형성하는 경우)에 전체 순위를 갖기 때문에 거의 최적입니다. F5의 성능은 입력 다항식의 순서와 작업 다항식의 증가와 고려되는 입력 다항식의 수 사이의 균형에 따라 달라지기 때문에 일반적인 용도로 F5를 조정하는 것은 어렵습니다. 현재까지(2022년), F4보다 훨씬 효율적인 분산 구현은 없지만, 예를 들어 HFE 챌린지를 깨는 등 여러 암호화 과제에 모듈식 정수 이상의 F5가 성공적으로 사용되었습니다.

이슈 5.는 그뢰브너 기반에서 시작되는 기저 변환 알고리즘의 발견으로 해결되었습니다. 또 다른 다항식 주문에 대한 그뢰브너 기반을 계산하기 위한 하나의 다항식 주문에 대한 그뢰브너 기반에서 시작됩니다. FGLM 알고리즘은 0차원의 경우(다항식이 유한 개의 복소수 공통 0을 갖는 경우)에만 작동하고 공통 0의 개수에서 다항식 복잡도를 갖는 기저 변환 알고리즘입니다. 일반적인 경우는 그뢰브너 워크 알고리즘이 기본 변환 알고리즘으로 작동합니다.^[4] 원래 형태에서 FGML은 관련 행렬의 희소성을 고려하지 않기 때문에 FGLM은 다항식 시스템을 해결하는 데 중요한 단계일 수 있습니다. 이는 희소 FGLM 알고리즘의 도입으로 해결되었습니다.^[5]

대부분의 범용 컴퓨터 대수 시스템은 그뢰브너 베이스에 대한 하나 또는 여러 알고리즘을 구현하고 있으며, 다항식의 시스템을 풀거나 삼각 함수를 단순화하는 등 다른 함수에도 종종 포함되어 있습니다. 예를 들어 CoCoA, GAP, Macaulay 2, Magma, Maple, Mathematica, SINGLE, SageMath와 SymPy. F4가 사용 가능한 경우 일반적으로 Buchberger의 알고리즘보다 훨씬 효율적입니다. 구현 기법과 알고리즘 변형은 효율성에 극적인 영향을 미칠 수 있지만 항상 문서화되지는 않습니다.

2022년^[update] 기준으로 F4와 (비공개)-FGLM의 가장 빠른 구현은 Msolve 라이브러리의 구현인 것 같습니다.^[6] Msolve는 그뢰브너 알고리즘 외에도 실제 루트 분리를 위한 빠른 알고리즘을 포함하고 있으며, 이 문제에 대한 다른 소프트웨어(메이플 및 마그마)를 크게 능가하는 다항식 시스템의 실제 솔루션에 대한 알고리즘에 이러한 모든 기능을 결합합니다.^[6] Msolve는 GitHub에서 사용할 수 있으며, Julia, Maple, SageMath와 인터페이싱됩니다. 이는 Msolve가 이러한 소프트웨어 환경 내에서 직접 사용할 수 있음을 의미합니다.

복잡성

그뢰브너 기반 계산의 복잡성은 일반적으로 변수의 수 n과 입력 다항식의 최대 차수 d의 관점에서 평가됩니다.

최악의 경우, 복잡성의 주요 매개변수는 결과적으로 감소된 그뢰브너 기저의 요소의 최대 정도입니다. 더 정확하게는, 그뢰브너 기저에 큰 차수 D의 요소가 포함된 경우, 이 요소는 계산에ω${\displaystyle {}^{}}$ω> D ω(n)의시간이 필요한$0$이 아닌 $항$을 포함할 수 있습니다.${\displaystyle$ \$Omega($D^{n}) >$D^{\Omega(n)}.$ 반면, 감소된 그뢰브너 기저의 모든 다항식이 최대 D의 차수를 갖는 경우, 그뢰브너 기저는 $차원{\displaystyle }$ O${\displaystyle (D^{}}$ n${\displaystyle {}^{}}$를 갖는 2D 미만 다항식의 벡터 공간에 대한 선형 대수에 의해 계산될 수 있습니다${\displaystyle .}$ ${\display O(D^{n}).$$}$따라서 이 계산의 복잡도는 $O{\displaystyle ({Dn}^{}}$ O${\displaystyle {(1)}^{}}$ $=$ ${\displaystyle {DO(n)}^{}}$ 입니다$.$ {\displaystyle O$(D$^{n})^{O(1)} $=$ D^{O(n$)}$입니다.

그뢰브너 기반 계산의 최악의 복잡성은 n에서 두 배 지수입니다. 더 정확하게 말하면, 복잡도는 d ${2{\mathrm{}}^{}}^{}$ ${n^{}}^{}$의 다항식${\textstyle$ d$^{2^{n}}$로 상한입니다.$}$따라서 o 표기법을 거의 사용하지 않으면 ${{d2}^{}}^{}$ ${n^{}}^{}$+ o${{(n)}^{}}^{}$로 제한됩니다${{}^{}}^{}$ ${\textstyle$ d$^{2^{n+o(n)}}.$ 반면, ${d2{}^{}}^{}$$ω$$($n), ${\textstyle d^{\Omega($n)}}의 다항식을 포함하는 축소된 그뢰브너 기저의 예가 제시되었습니다.$}$또는 ${d2}^{}$$ω$(n) ${\textstyle d^{\Omega($n)}}개 요소를 포함합니다. 그뢰브너 기반을 계산하기 위한 모든 알고리즘은 결과를 작성해야 하기 때문에 복잡성의 하한을 제공합니다.

그뢰브너 기저는 EXPSPACE-완전입니다.^[7]

일반화

그뢰브너 베이스의 개념과 알고리즘은 다항식 링 위에서 자유 모듈의 하위 모듈로 일반화되었습니다. 실제로, L이 링 R 위의 자유 모듈이라면, L의 두 원소의 $곱$을 0으로 정의함으로써 직접합 ${\displaystyle R}$ ⊕ L ${\displaystyle$ R\opplus L}을 링으로 간주할 수 있습니다. 이 링은 $R{\displaystyle }$[${\displaystyle {}_{}}$ ${\displaystyle 1_{}}$…,${\displaystyle {}_{}]}$ /${\displaystyle }$⟨ {$e$ i${\displaystyle j}$ ${\displaystyle 1}$ ${\displaystyle \le }$ i ${\displaystyle \le }$j $≤$ l} ⟩${\displaystyle$R$[e_{$1},\$ldots,e_${l$}]/\left\langle$\{$e_{i$}e_{$j}$1$\leq$i\$leq$j\$leq$ l$\backslash \}\backslash$right\${\displaystyle {rangle}_{}\}}$로 식별할 수 있습니다${\displaystyle .}$ ${\displaystyle {여기}_{}}$서$$e 1, …, e${\displaystyle e_{$1},\ldots,e_{l}}는 L의 기초입니다. 이를 통해 $g{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$${\displaystyle \dots ,}$${\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$$, g_{k}}$에 의해 생성된 L의 하위 모듈을 $R{\displaystyle }$[${\displaystyle e_{}}$ 1${\displaystyle {}_{}\dots ,}$ ${\displaystyle {}_{}}$ ${\displaystyle$ R$[e_{1},\ldots, e_{l}]}$에 의해 생성된 L의 하위 모듈을 식별할 수 있습니다$.$$g_{k}}$ 및$$ 곱 $e{\displaystyle {}_{}}$ ${\displaystyle {ee}_{}}$ ee ${\$ $1{\displaystyle \mathrm{}}$ ${\displaystyle \le }$ ${\displaystyle i}$ ${\displaystyle \le }$ ${\displaystyle j}$ ${\displaystyle \le }$ l ${\displaystyle$ 1$\leqi\leq j\leql}$입니다$.$ R이 다항식 링인 경우, 이는 모듈의 그뢰브너 베이스의 이론과 알고리즘을 이상의 그뢰브너 베이스의 이론과 알고리즘으로 축소합니다.

그뢰브너 베이스의 개념과 알고리즘은 또한 주요 이상적 고리 또는 바일 대수에 대한 다항식 고리와 같이 교환적이든 아니든 다양한 고리에 대한 이상으로 일반화되었습니다.

응용분야

오류 정정 코드

그뢰브너 기반은 대수적 디코딩을 위한 오류 수정 코드 이론에 적용되었습니다. 다양한 형태의 오류 수정 방정식에 대한 그뢰브너 기반 계산을 사용하여 순환 코드,^[8] 아핀 품종 코드,^[9] 대수 기하학 코드 및 일반 선형 블록 코드의 오류를 수정하기 위한 디코딩 방법이 개발되었습니다.^[10] 대수 디코딩에서 그뢰브너 기반을 적용하는 것은 여전히 채널 코딩 이론의 연구 영역입니다.

참고 항목

참고문헌

더보기

• Adams, William W.; Loustaunau, Philippe (1994). An Introduction to Gröbner Bases. Graduate Studies in Mathematics. Vol. 3. American Mathematical Society. ISBN 0-8218-3804-0.
• Li, Huishi (2011). Gröbner Bases in Ring Theory. World Scientific. ISBN 978-981-4365-13-0.
• Becker, Thomas; Weispfenning, Volker (1998). Gröbner Bases: A Computational Approach to Commutative Algebra. Graduate Texts in Mathematics. Vol. 141. Springer. ISBN 0-387-97971-9.
• Buchberger, Bruno (1965). An Algorithm for Finding the Basis Elements of the Residue Class Ring of a Zero Dimensional Polynomial Ideal (PDF) (PhD). University of Innsbruck. — (2006). Translated by Abramson, M. "Bruno Buchberger's PhD thesis 1965: An algorithm for finding the basis elements of the residue class ring of a zero dimensional polynomial ideal". Journal of Symbolic Computation. 41 (3–4): 471–511. doi:10.1016/j.jsc.2005.09.007. [이것은 그뢰브너 기지를 발명한 부흐베르거의 논문입니다.]
• Buchberger, Bruno (1970). "An Algorithmic Criterion for the Solvability of a System of Algebraic Equations" (PDF). Aequationes Mathematicae. 4: 374–383. doi:10.1007/BF01844169. S2CID 189834323. (이것은 부흐베르거의 논문 저널 출판입니다.)Burchberger, B.; Winkler, F., eds. (26 February 1998). "An Algorithmic Criterion for the Solvability of a System of Algebraic Equations". Gröbner Bases and Applications. London Mathematical Society Lecture Note Series. Vol. 251. Cambridge University Press. pp. 535–545. ISBN 978-0-521-63298-0.
• Buchberger, Bruno; Kauers, Manuel (2010). "Gröbner Bases". Scholarpedia. 5 (10): 7763. Bibcode:2010SchpJ...5.7763B. doi:10.4249/scholarpedia.7763.
• Fröberg, Ralf (1997). An Introduction to Gröbner Bases. Wiley. ISBN 0-471-97442-0.
• Sturmfels, Bernd (November 2005). "What is ... a Gröbner Basis?" (PDF). Notices of the American Mathematical Society. 52 (10): 1199–1200, a brief introduction{{cite journal}}: CS1 메인: 포스트스크립트 (링크)
• Shirshov, Anatoliĭ I. (1999). "Certain algorithmic problems for Lie algebras" (PDF). ACM SIGSAM Bulletin. 33 (2): 3–6. doi:10.1145/334714.334715. S2CID 37070503. Sibirsk에서 번역됨. Mat. Zh. 시베리아 수학 저널 3 (1962), 292–296).
• Aschenbrenner, Matthias; Hillar, Christopher (2007). "Finite generation of symmetric ideals". Transactions of the American Mathematical Society. 359 (11): 5171–92. arXiv:math/0411514. doi:10.1090/S0002-9947-07-04116-5. S2CID 5656701. (무한 차원에서 무한히 많은 불확정 상태의 다항식 고리에 대한 그뢰브너 기저).

외부 링크

• F4 알고리즘에 대한 Faugère의 자체 구현
• "Gröbner basis", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Buchberger, B. (2003). "Gröbner Bases: A Short Introduction for Systems Theorists" (PDF). In Moreno-Diaz, R.; Buchberger, B.; Freire, J. (eds.). Computer Aided Systems Theory — EUROCAST 2001: A Selection of Papers from the 8th International Workshop on Computer Aided Systems Theory. Springer. pp. 1–19. ISBN 978-3-540-45654-4.
• Buchberger, B.; Zapletal, A. "Gröbner Bases Bibliography".
• Gröbner Bases 소프트웨어의 비교 타이밍 페이지
• 브루노 부흐베르거 교수
• Weisstein, Eric W. "Gröbner Basis". MathWorld.
• 스콜라피디아에 관한 그뢰브너 기초 소개