리만 곡률 텐서
Riemann curvature tensor미분 기하학의 수학적 분야에서는 리만 곡률 텐서 또는 리만-크리스토펠 텐서(Bernhard Riemann, Elwin Bruno Christofel 이후)가 리만 다지관의 곡률을 표현하는 데 사용되는 가장 일반적인 방법이다. 리만 매니폴드의 각 지점(즉, 텐서 필드)에 텐서를 할당한다. 두 번째 공변량 파생상품의 통근 실패를 측정하는 리만 지표의 현지 불변량이다. 리만 다지관은 평평한 경우에만, 즉 유클리드 공간에 대한 국부 등축이 0이다.[1] 곡률 텐서는 또한 모든 사이비-리만 다지관 또는 실제로 아핀 연결이 장착된 다지관에 대해 정의될 수 있다.
일반상대성이론, 현대중력론에서 중심수학적 도구로, 스페이스타임의 곡률성은 원칙적으로 지오데틱 편차 방정식을 통해 관측할 수 있다. 곡률 텐서는 자코비 방정식에 의해 정밀하게 만들어진 의미에서 지오데틱을 따라 움직이는 강체 신체가 경험하는 조력력을 나타낸다.
정의
Let (M, g)는 리만족 또는 사이비-리만족 다지관이고, (은 M에 있는 모든 벡터장의 공간이다. We define the Riemann curvature tensor as a map by the following formula[2] which is in terms of the Levi-Civita connection :
또는 동등하게
여기서 [X, Y]는 벡터 필드의 Bracket이고 [ , Y 은(는) 차등 연산자의 정류자다. 각 접선 벡터 쌍에 대해 v, R(u, v)은 다지관의 접선 공간의 선형 변환이다. u와 v로 선형이며, 텐서(tensor)를 정의한다. 때때로 곡률 텐서는 반대 기호로 정의된다.
= / X x Y= / Y x이 좌표 벡터 필드인경우 [ Y = {\은 다음과 같다
곡률 텐서는 공변량 파생상품의 비확정성을 측정하며, 이와 같이 유클리드 공간(이 맥락에서 평탄한 공간이라 함)과의 이소계 존재에 대한 통합성 장애물이다. ( ,v) 이 있는 선형 변환을 곡률 변환 또는 내형 변환이라고도 한다.
곡률 공식은 또한 다음과 같이 정의된 두 번째 공변량 파생상품의 용어로 표현할 수 있다.[3]
u와 v로 선형이다. 다음:
따라서 비조정 벡터 u와 v의 일반적인 경우, 곡률 텐서는 두 번째 공변량 파생상품의 비확정성을 측정한다.
기하학적 의미
비공식적으로
테니스 코트와 지구를 비교해 보면 곡면 공간의 효과를 알 수 있다. 테니스 코트의 오른쪽 하단 모서리에서 시작하며, 북쪽을 향해 라켓이 돌출되어 있다. 그런 다음 코트의 윤곽선을 따라 걸을 때 각 단계에서 테니스 라켓이 이전 위치와 평행하게 동일한 방향으로 유지되도록 하십시오. 루프가 완료되면 테니스 라켓이 초기 출발 위치와 평행하게 된다. 테니스 코트가 만들어져 표면이 평평하기 때문이다. 반면에, 지구의 표면은 곡선이다: 우리는 지구 표면의 고리를 완성할 수 있다. 적도에서 시작하여 지구 표면을 따라 테니스 라켓을 북쪽으로 향한다. 다시 한 번 테니스 라켓은 수평선의 로컬 평면을 기준으로 하여 항상 이전 위치와 평행하게 유지되어야 한다. 이 길을 위해서는 먼저 북극으로 걸어가다가 90도 방향을 틀고 적도로 내려가고, 마침내 90도 방향을 틀고 다시 출발점으로 걸어간다. 그러나 이제 테니스 라켓은 뒤쪽을 가리키게 될 것이다. 이 프로세스는 경로를 따라 벡터를 병렬로 운반하는 것과 유사하며, 그 차이는 "직선"으로 보이는 선이 국소적으로 "직선"인 방법을 식별한다. 루프가 완료될 때마다 테니스 라켓은 표면의 거리와 곡률에 따라 양만큼 초기 위치에서 더 멀리 꺾인다. 평탄한 공간에서처럼 평행 운송이 가능한 곡선 표면을 따라 경로를 식별할 수 있다. 이것들은 우주의 지오데틱인데, 예를 들어 구형의 큰 원의 어떤 부분이라도 그렇다.
수학에서 곡선의 공간 개념은 회화용어와 다르다. 예를 들어, 만약 위의 과정이 실린더에서 완료되었다면, 실린더 주위의 곡률이 실린더를 따라 평탄도와 함께 상쇄되기 때문에 전체적으로 곡선이 아니라는 것을 알게 될 것이다. 이는 가우스 곡률과 가우스-보넷 정리의 결과물이다. 이것의 익숙한 예는 플로피 피자 조각으로, 그것의 너비를 따라 구부러지면 그것의 길이를 따라 단단하게 유지될 것이다.
리만 곡률 텐서(Riemann 곡률 텐서)는 내적인 곡률의 측정치를 포착하는 방법이다. (벡터의 성분을 적는 것과 같은) 성분으로 적으면, 그것은 다차원적인 집합과 부분파생물의 생산물로 구성된다. (그 부분파생상품들 중 일부는 곡면 위에서 직선으로 걷는 사람에게 부과되는 곡률을 포착하는 것과 같다고 생각할 수 있다.)
정식으로
유클리드 공간의 벡터가 루프를 중심으로 평행하게 이동하면 원래의 위치로 돌아간 후 다시 초기 방향을 가리키게 된다. 그러나 이 재산은 일반적인 경우에 해당하지 않는다. 리만 곡률 텐서(Riemann 곡률 텐서)는 일반 리만 다양체에서 이것의 실패를 직접 측정한다. 이 고장을 다지관의 비홀로니(nonholony)라고 한다.
x는t 리만 다지관 M에서 곡선이 되게 하라. τxt : TMx0 → TMxt x를t 따라 평행 운송 맵을 나타낸다. 병렬 전송 맵은 다음에 의해 공변량 파생 모델과 관련된다.
곡선을 따라 정의된 각 벡터 필드 Y에 대해
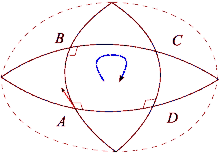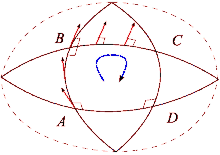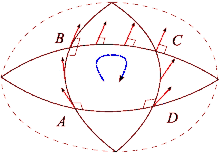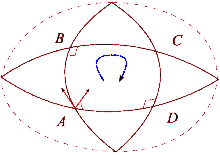
X와 Y가 통근 벡터 필드의 한 쌍이라고 가정하자. 이러한 각 장은 x의0 근방에 1-모수 차이점들을 생성한다. 각각tX X와 Y의tY 흐름을 따라 시간 t에 대한 병렬 전송을 한다. 벡터 Z tmx0 TM의 측면 tY, SX, -tY, -sX를 중심으로 한 병렬 전송은 다음과 같다.
이것은 접선 공간 TM에서x0 Z를 원래 위치로 되돌리기 위한 병렬 이송의 실패를 측정한다. s → t → 0을 전송하여 루프를 축소하면 이 편차에 대한 최소한의 설명이 제공된다.
여기서 R은 리만 곡률 텐서다.
좌표식
텐서 지수 표기법으로 변환하는 Riemann 곡률 텐서는 다음과 같이 주어진다.
여기서 = / 은 좌표 벡터 필드다. 위의 표현은 Christoffel 기호를 사용하여 쓸 수 있다.
(리만 기하학의 공식 목록도 참조).
Riemann 곡률 텐서는 임의의 탐촉자 의 공변량 파생물의 정류자이기도 하다.[4][5]
since the connection is torsionless, which means that the torsion tensor vanishes.
이 공식은 흔히 리치 정체성이라고 불린다.[6] 리치와 레비시비타가 리만 곡률 텐서(Riemann 곡률 텐서)의 표현을 얻기 위해 사용하는 고전적인 방법이다.[7] 이와 같이 수량 { { { { { { { R의 텐서 특성이 증명된다.
이 정체성은 다음과 같이 임의 텐터의 두 공변량 파생상품에 대한 정류자를 얻기 위해 일반화할 수 있다.
이 공식은 또한 변경 없는 텐서 밀도에도 적용된다. 왜냐하면 Levi-Civita (일반적이지 않은) 연결의 경우 다음과 같이 되기 때문이다.[6]
어디에
또한 때때로 다음과 같이 순전히 공변량 버전을 정의하는 것이 편리하다.
대칭 및 ID
리만 곡률 텐서에는 다음과 같은 대칭과 정체성이 있다.
| 스큐 대칭 | ||
|---|---|---|
| 스큐 대칭 | ||
| 첫 번째(알제브라질) 비안치 정체성 | ||
| 교환대칭 | ||
| 두 번째(차동) 비안치 정체성 |
여기서 괄호 , 은 미터법 텐셔에 의해 유도된 접선 공간의 내부 제품을 가리킨다.
제1(알제브라질) 비안치 정체는 리치에 의해 발견되었지만, 아래 비안치 정체와 비슷하게 보이기 때문에 흔히 제1비안치 정체 또는 대수비안치 정체라고 불린다.(또한 비안치 정체는 제1비안치 정체는 토션 텐서(torsion tensor)의 차등 정체가 된다). 흔히 다음과 같이 쓰여 있다.
처음 세 개의 정체성은 곡률 텐서 전체 대칭 리스트를 형성한다. 즉, 위의 정체성을 만족하는 어떤 텐서라도 주어진다면, 어느 시점에서 그러한 곡률 텐서(tensor)를 가진 리만 다지관을 발견할 수 있다. 단순 계산에 따르면 이러한 텐서는 ( - )/ 개의 독립 구성요소를 가지고 있다.[9] 이것들로부터 상호 대칭이 뒤따른다. 대수 대칭도 R이 칸막이 2+2에 해당하는 영 대칭체의 이미지에 속한다고 말하는 것과 동등하다.
리만족 다지관에서는 공변량 파생상품 R 을 가지고 있으며, 비안치 정체성(흔히 제2의 비안치 정체성 또는 차등 비안치 정체성)은 표의 마지막 정체성의 형태를 취한다.
리치 곡률
리치 곡률 텐서(Ricci 곡률 텐서)는 리만 텐서만 텐서(Riemann tensor)의 제1지수와 제3지수의 수축이다.
특례
표면
2차원 표면의 경우, 비안치 정체성은 리만 텐서가 하나의 독립적 요소만을 가지고 있다는 것을 의미하며, 이는 리치 스칼라가 리만 텐서를 완전히 결정한다는 것을 의미한다. 리만 텐서에는 필요한 대칭에 맞는 유효한 식이 하나만 있다.
메트릭스를 두 번 계약함으로써 명시적 형식을 찾을 수 있다.
여기서 는 미터법 이고 K= / 은 가우스 곡률이라고 하는 함수이며 a, b, c 및 d는 1 또는 2 값을 취한다. 리만 텐서에는 기능적으로 독립적인 요소가 하나만 있다. 가우스 곡률은 표면의 단면 곡률과 일치한다. 또한 표면의 Ricci 곡률 텐서(tensor)는 간단히 주어지는 반면, 2-manifold의 스칼라 곡률의 정확히 절반이다.
공간 양식
리만 다지관은 그것의 단면 곡률이 상수 K와 같다면 우주 형태다. 리만 텐서(Riemann tensor of a space form)는 에 의해 주어진다.
반대로 치수 2를 제외하고, 리만 다지관의 곡률이 어떤 기능 K에 대해 이 형식을 가지고 있다면, 비안치 정체성은 K가 일정하고 따라서 다지관이 (로컬하게) 공간 형태라는 것을 암시한다.
참고 항목
인용구
- ^ Lee 2018, 페이지 193.
- ^ Lee 2018, 페이지 196.
- ^ Lawson, H. Blaine, Jr.; Michelsohn, Marie-Louise (1989). Spin Geometry. Princeton U Press. p. 154. ISBN 978-0-691-08542-5.
- ^ Synge J.L., Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 83, 107. ISBN 978-0-486-63612-2.
- ^ P. A. M. Dirac (1996). General Theory of Relativity. Princeton University Press. ISBN 978-0-691-01146-2.
- ^ Jump up to: a b Lovelock, David; Rund, Hanno (1989) [1975]. Tensors, Differential Forms, and Variational Principles. Dover. p. 84,109. ISBN 978-0-486-65840-7.
- ^ Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications", Mathematische Annalen, 54 (1–2): 125–201, doi:10.1007/BF01454201
- ^ Sandberg, Vernon D (1978). "Tensor spherical harmonics on S 2 and S 3 as eigenvalue problems" (PDF). Journal of Mathematical Physics. 19 (12): 2441–2446. Bibcode:1978JMP....19.2441S. doi:10.1063/1.523649.
- ^ Bergmann P.G. (1976). Introduction to the Theory of Relativity. Dover. pp. 172–174. ISBN 978-0-486-63282-7.
참조
- Lee, John M. (2018). Introduction to Riemannian Manifolds. Springer-Verlag. ISBN 978-3-319-91754-2.
- Besse, A.L. (1987), Einstein Manifolds, Springer, ISBN 0-387-15279-2
- Kobayashi, S.; Nomizu, K. (1963), Foundations of Differential Geometry, 1, Interscience
- Misner, Charles W.; Thorne, Kip S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0





![{\displaystyle R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a30a969d5b599e29c8ef7fc0344b823845e5865)
![{\displaystyle R(X,Y)=[\nabla _{X},\nabla _{Y}]-\nabla _{[X,Y]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6213ec08b244f551f3abb12fd05c9352ea337d08)
![{\displaystyle [\nabla _{X},\nabla _{Y}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f14a9375ccac5a4b17f4da5a35e2fab48e427930) (는) 차등 연산자의 정류자다. 각 접선 벡터 쌍에 대해 v, R(u, v)은 다지관의 접선 공간의 선형 변환이다. u와 v로 선형이며, 텐서(tensor)를 정의한다. 때때로 곡률 텐서는 반대 기호로 정의된다.
(는) 차등 연산자의 정류자다. 각 접선 벡터 쌍에 대해 v, R(u, v)은 다지관의 접선 공간의 선형 변환이다. u와 v로 선형이며, 텐서(tensor)를 정의한다. 때때로 곡률 텐서는 반대 기호로 정의된다. 
 좌표 벡터 필드인
좌표 벡터 필드인![{\displaystyle [X,Y]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d09ccf5fa5768a8ccddbf244b6652de1dc8f0ce)






![{\displaystyle \left.{\frac {d}{ds}}{\frac {d}{dt}}\tau _{sX}^{-1}\tau _{tY}^{-1}\tau _{sX}\tau _{tY}Z\right|_{s=t=0}=\left(\nabla _{X}\nabla _{Y}-\nabla _{Y}\nabla _{X}-\nabla _{[X,Y]}\right)Z=R(X,Y)Z}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7391c086a496cf8c270adf768cd477a32fb05b)

 좌표 벡터 필드다. 위의 표현은
좌표 벡터 필드다. 위의 표현은 
 공변량 파생물의
공변량 파생물의 



![{\displaystyle {\begin{aligned}&\nabla _{\delta }\nabla _{\gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}-\nabla _{\gamma }\nabla _{\delta }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}\\[3pt]={}&R^{\alpha _{1}}{}_{\rho \delta \gamma }T^{\rho \alpha _{2}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}+\ldots +R^{\alpha _{r}}{}_{\rho \delta \gamma }T^{\alpha _{1}\cdots \alpha _{r-1}\rho }{}_{\beta _{1}\cdots \beta _{s}}-R^{\sigma }{}_{\beta _{1}\delta \gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\sigma \beta _{2}\cdots \beta _{s}}-\ldots -R^{\sigma }{}_{\beta _{s}\delta \gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s-1}\sigma }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711ad8f7e44966802efd57caabfa504dcdab7c79)








![{\displaystyle R_{abcd}+R_{acdb}+R_{adbc}=R_{a[bcd]}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17934a6813e0b9f2a4d72dcf93a8ad42d9eae199)



![{\displaystyle R_{abcd;e}+R_{abde;c}+R_{abec;d}=R_{ab[cd;e]}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14773d3be1cd12575931011085c4b9fd32441ca7)

![{\displaystyle R_{a[bcd]}=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf2451d085ded22bb92db17bfe13d8725a9cb320)

 가지고 있으며,
가지고 있으며, 







