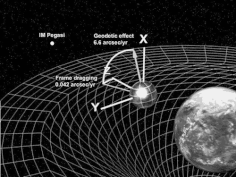
측지 효과

측지학적 효과(지질학적 세차, 드 시터 세차 또는 드 시터 효과라고도 함)는 일반 상대성 이론으로 예측된 시공간 곡률이 궤도를 도는 물체와 함께 운반되는 벡터에 미치는 영향을 나타낸다.예를 들어, 벡터는 중력 탐사선 B 실험에 의해 수행된 것처럼 지구 궤도를 도는 자이로스코프의 각 운동량일 수 있습니다.측지학적 효과는 1916년 빌렘 드 시터에 의해 처음 예측되었는데, 그는 지구-달계의 움직임에 상대론적 수정을 제공했다.De Sitter의 작업은 1918년 Jan Schouten에 의해 그리고 1920년 Adrian Fokker에 ^[1]의해 확장되었습니다.또한 라플라스-룽지-렌즈 ^[2]벡터의 회전과 동등한 천문학 궤도의 특정한 영속적인 세차 운동에도 적용할 수 있다.

지오데틱 효과라는 용어는 움직이는 물체가 회전하고 있을 수도 있고 회전하지 않을 수도 있기 때문에 두 가지 약간 다른 의미를 가지고 있습니다.회전하지 않는 물체는 측지학에서 움직이는 반면 회전하는 물체는 약간 다른 ^[3]궤도로 움직인다.

드 시터 세차운동과 렌스의 차이점-세차운동(프레임 드래그)은 드 시터 효과가 단순히 중심 질량의 존재에 기인하는 반면 렌즈는-세차운동이 일어나는 것은 중심질량의 회전 때문이다.총 세차운동은 드 시터 세차운동과 렌즈 세차운동을 조합하여 계산한다.삼키는 세차 운동.

실험적인 확인

지구궤도에서 ^[4]자이로스코프의 스핀축 기울기를 측정하는 실험인 중력탐사선 B에 의해 0.5% 이상의 정밀도로 지오데틱 효과가 검증되었다.첫 번째 결과는 2007년 4월 14일 미국물리학회 ^[5]회의에서 발표되었습니다.

공식

일반상대성이론
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }=t_{\mu \nu }}$
서론 역사 수학 공식화 테스트
기본 개념 등가원칙 특수상대성이론 월드 라인 유사 리만 다양체
현상 케플러 문제 중력 렌즈 중력파 프레임 드래그 측지 효과 이벤트 호라이즌 특이점 블랙홀 시공간 시공간도 민코프스키 시공간 아인슈타인-로젠 다리
방정식 형식주의 방정식 선형 중력 아인슈타인 장 방정식 프리드만 측지학 매티슨-파페트루-딕슨 해밀턴-야코비-아인슈타인 형식주의 ADM BSSN 포스트뉴턴어 고급 이론 칼루자-클레인 이론 양자 중력
솔루션 슈바르츠실트(내부) 리스너-노르드스트롬 괴델 커 커-뉴먼 카스너 레마슈트르톨만 타우부 너트 밀른 로버트슨-워커 pp파 반스톡툼 더스트 바일루이스파파페트로우
과학자 아인슈타인 로렌츠 힐베르트 푸앵카레 슈바르츠실트 드 시터 리스너 노드스트롬 와일 에딩턴 프리드먼 밀른 즈위키 레마슈트르 괴델 휠러 로버트슨 바딘 워커 커 찬드라세카르 엘러스 펜로즈 호킹 레이쇼후리 테일러 헐스 반 스톡텀 타우브 뉴먼 야우 손 다른이들
물리 포털 카테고리
v t

세차운동을 유도하기 위해 시스템이 회전하는 슈바르츠실트 메트릭에 있다고 가정합니다.회전하지 않는 메트릭은

${{displaystyle ds^{2}=dt^{2}\left(1-{\frac {2m}{r}}\right)-dr^{2}\left(1-{\frac {2m}{r}}\r^2}(d\theta ^{2}+\sin ^{2}\ta ^{d} } } ^2 phi},$

여기서 c = G = 1 입니다.

velocity = π/2 평면에서 원형$궤도$에 있는 위성이 정지 상태를 유지할 수 있도록 $각속도{\displaystyle }$ ${\$ \$displaystyle$ \omega$$}의 회전 좌표계를 도입하였습니다.이것은 우리에게

$\displaystyle d\phi = d\phi '-\obega \,dt.}$

이 좌표계에서 반경 위치 r의 관찰자는 r에 위치하는 벡터가 각주파수 θ로 회전하고 있다고 본다.그러나 이 관찰자는 상대론적 시간 연장으로 인해 r의 다른 값에 위치한 벡터가 다른 속도로 회전하는 것으로 본다.슈바르츠실트 메트릭을 회전 프레임으로 변환하고$\delta {\displaystyle }$(\$displaystyle \theta)$를 상수라고 가정하면

${\displaystyle {dsarred}&=left(1-{\frac {2m}{r}}-r^{2}\right)\left(dt-{\frac {r^2}\display \m/r^{2}\display \ope }{1-2m/r-r^{2}\d}\light}, ph}\d$

${\displaystyle {\beta }^{}}$ $=$ ${\displaystyle {sin\mathrm{}}^{}}$ 2${\displaystyle }$µ ($θ$) { displaystyle $\sin$ =\$sin$^{$2}(theta$이다. β = δ/2 평면에서 공전하는 물체의 경우, β = 1을 가지며, 물체의 세계선은 항상 일정한 공간 좌표를 유지합니다.이제 메트릭은 표준 형식입니다.

$\displaystyle ds^{2}=e^{2\Phi }\left(dt-w_{i},dx^{i}\right)^{2}-k_{ij},dx^{i},dx^{j}.}$

이 표준 형태로부터, 우리는 자이로스코프의 회전 속도를 적시에 쉽게 결정할 수 있다.

${\displaystyle\begin{aligned}\Omega&={displayfrac{4}}e^{\}Phi } [k^{ik}k^{jl}(\obmega_{i,j}-\obmega_{j,i})(\obmega_{k,l}-\obmega_{l,k})^{1/2}=\\\\\\\\nambracrcrcrcrcrcrcr(r-3m){r}{rcrcrcrcr}\m}\{{{{n}^2-i}\end { aligned}}$

여기서 마지막 등식은 가속이 없는 자유낙하 관찰자에 대해서만 참이므로${\displaystyle {}_{}}\delta {\displaystyle \mathrm{}}$ $=$ ${\displaystyle 0}$(\$displaystyle \Phi,_{i$}=$0$입니다.이로 인해

$(\displaystyle \Phi,_{i}=black {2m/r^{2}-2r\displayfrac {2m/r-r^{2}\black \obe \obe ^{2}}}}= 0 .$

이 방정식을 δ 수율에 대해 푸는 방법

${\displaystyle \obega ^{2}=black {m}{r^{3}\black}}.}$

이것은 본질적으로 케플러의 주기 법칙이며, 이 특정한 회전 좌표계의 시간 좌표 t로 표현될 때 상대론적으로 정확합니다.회전 프레임에서는 위성은 정지해 있지만, 위성에 탑승한 관찰자는 자이로스코프의 각운동량 벡터가 θ의 속도로 세차하고 있는 것을 볼 수 있다.이 관측자는 또한 먼 별들이 회전하는 것으로 보지만, 시간적 팽창으로 인해 약간 다른 속도로 회전합니다.θ를 자이로스코프의 적절한 시간으로 하자.그리고나서

$\displaystyle \Delta \delta =\left(1-{\frac {2m}{r}}-r^{2}\display \ope \ ^{2}\right)^1/2}, dt=\left(1-{\frac {3m}{r}}\right)^1/2}, dt.}$

-2m/r 항은 중력 시간 확대로 해석되며, 추가 -m/r은 기준 프레임의 회전 때문이다.α'를 회전 프레임의 누적 세차 운동이라고 하자.α ${\displaystyle {\prime }^{}}$ ${\displaystyle =}$ ${\displaystyle \mathrm{\omega }}$ τ ${\displaystyle \tau }$ τ$（$ \$displaystyle$ \$alpha$ ' $=$\ $Omega$ \ $Delta$ \ delta$}$） $since{\displaystyle {}^{}}$ α α α α α α α 、 α stars , 、 , , , , 、 , since since since since since since since since 、

$(\displaystyle \alpha '+2\pi =-2\pi {\bigg (}\left (1-{\frac {3m}{r}}\오른쪽)^{1/2}-1{\Bigg}}}}}).}$

1차 테일러 시리즈에서는

${\displaystyle \alpha \약 {3\pi m}{r}}{\fracrt {3\pi m}{r}}\sin(\theta).}$

토마스 세차 운동

사람들은 드 시터 세차운동을 중력으로 휘어진 시공간에서 비롯된 기하학적 효과와 결합된 토마스 세차라고 불리는 운동학적 효과로 분해하려고 시도할 수 있다.적어도 한 저자는^[6] 이렇게 묘사하지만, 다른 이들은 "토마스의 세차운동은 지구 표면의 자이로스코프에 적용되지만 자유롭게 움직이는 ^[7]위성의 자이로스코프에는 적용되지 않는다"고 말한다.전자의 해석에 대한 반대는 요구되는 토마스 세차운동이 잘못된 부호를 가지고 있다는 것이다.페르미-워커 전달^[8] 방정식은 측지 효과와 토마스 세차 운동을 모두 제공하며 곡면 시공간에서 가속 운동을 위한 스핀 4벡터의 전달을 기술한다.스핀 4-벡터는 속도 4-벡터와 직교합니다.페르미-워커 전송은 이 관계를 유지합니다.가속이 없다면 페르미-워커 이동은 측지학을 따라 평행하게 이동하며 측지 효과로 인해 스핀 세차 운동을 제공합니다.평평한 민코프스키 시공간에서 균일한 원형 운동으로 인한 가속도의 경우, 페르미 워커 운송은 토마스 세차 운동을 제공한다.

「 」를 참조해 주세요.

• 프레임 드래그
• 일반상대성이론의 측지학
• 중력 우물
• 중력 물리학과 상대성 이론의 연표

메모들

레퍼런스

• 볼프강 린들러(2006) 상대성: 특수, 일반, 우주론(제2판), 옥스퍼드 대학 출판부, ISBN 978-0-19-856731-8

외부 링크

• NASA와 스탠포드 대학의 중력 탐사선 B 웹사이트
• 곡면공간에서의 세차운동 "지오데틱 효과"
• 측지 효과