스페이스타임 다이어그램
Spacetime diagram
| 다음에 대한 시리즈 일부 |
| 스페이스타임 |
|---|
 |
스페이스타임 도표는 특수 상대성 이론에서 공간과 시간의 특성을 그래픽으로 나타낸 것이다. 스페이스타임 다이어그램은 수학 방정식이 없는 시간 팽창과 길이 수축과 같은 해당 현상을 정성적으로 이해할 수 있게 한다.
물체의 위치의 역사는 항상 물체의 세계선이라고 불리는 선을 스팩타임 도표로 추적한다. 스페이스타임 다이어그램의 점은 공간과 시간의 고정된 위치를 나타내며 이벤트라고 한다.
가장 잘 알려진 스팩타임 도표는 1908년 헤르만 민코프스키가 개발한 민코프스키 도표로 알려져 있다. 밍코우스키 도표는 1개의 공간 차원과 1개의 시간 차원으로 구성된 우주에서 일어나는 사건을 나타내는 2차원 그래프다. 일반 거리 시간 그래프와 달리 수평 축에는 거리가 표시되고 수직 축에는 시간이 표시된다. 또한 빛의 속도로 움직이는 물체가 다이어그램의 축에 45° 각도를 따르는 것으로 묘사되도록 시간과 공간 단위를 선택한다.
키네틱 다이어그램 소개
위치 대 시간 그래프
1차원 운동학 연구에서 위치 대 시간 그래프(거리 대 시간 그래프 또는 p-t 그래프라고도 함)는 운동을 설명하는 유용한 수단을 제공한다. 물체의 움직임의 특정한 특징은 선의 형태와 기울기로 증명된다.[1] 그림 1-1에서 표시된 물체는 6초 동안 1.66m/s의 균일한 속도로 원점에서 벗어나 5초 동안 정지한 다음, 일정하지 않은 속도로 7초 동안 원점으로 되돌아간다.
가장 기본적인 수준에서 스페이스타임 다이어그램은 시간 대 위치 그래프에 불과하며, 일반적인 p-t 그래프에서 축의 방향이 교환된다. 즉, 수직축은 시간 및 수평축을 공간 좌표값으로 나타낸다. 특히 특수상대성(SR)에서 사용할 경우, 스페이스타임 도표의 시간 축은 광 c의 속도에 따라 크기가 조정되므로 ct로 라벨을 붙이는 경우가 많다. 이것은 공간 축과 관련된 치수에 따라, 자주 x로 표기되는, 어드레싱되는 물리량의 치수를 <시간>에서 <길이>로 바꾼다.
기준 프레임의 표준 구성
관찰자가 서로 다른 기준 프레임에서 측정한 스페이스타임 좌표를 서로 비교하는 방법에 대한 통찰력을 높이려면 단순화된 설정으로 작업하는 것이 유용하다. 주의해서, 이것은 도달한 결론의 일반성을 잃지 않고 수학을 단순화할 수 있다. 시간적 구성요소를 잠시 제쳐두면, 두 개의 갈릴레이 기준 프레임(즉, 기존의 3공간 프레임), S와 S'("준비"로 발음됨) 각각 각 프레임에 관측자 O와 O'가 정지되어 있지만, 다른 하나를 속도 ±v로 움직이는 것으로 측정하는 것은 다음과 같은 경우 표준 구성이라고 한다.
- 프레임 S의 x, y, z축은 프레임 S의 각 프라이밍 축과 평행하게 방향을 정한다.
- 프레임 S′는 프레임 S에서 측정한 대로 등속 v로 프레임 S의 x 방향으로 이동한다.
- 프레임 S와 프레임 S의 기원은 프레임 S에서 시간 t = 0, 프레임 S에서 t′ = 0에 대해 일치한다.[2]: 107
이 공간 설정은 그림 1-2에 표시되며, 시간 좌표는 수량 t와 t'로 별도로 주석을 달았다.
단순화의 추가 단계에서는 흔히 관찰된 움직임의 방향만 고려하고 다른 두 공간 구성요소는 무시하는 것이 가능하여 위에서 소개한 바와 같이 x와 ct를 2차원 스페이스타임 다이어그램으로 표시할 수 있다.
비-relativistic "spacetime 다이어그램"
그림 1-3에 x와 ct라고 표시된 검은색 축은 관찰자의 좌표계로 '정지 중'이라고 하며 x = 0에 위치한다. 이 관찰자의 세계선은 ct 시간축과 동일하다. 이 축에 대한 각 평행선은 정지해 있는 물체와도 일치하지만 다른 위치에 있을 것이다. 파란색 선은 움직이는 관찰자와 같이 일정한 속도 v로 오른쪽으로 움직이는 물체를 묘사한다.
ct′라고 표시된 이 파란색 선은 두 번째 관찰자의 시간 축으로 해석될 수 있다. 두 관측자가 동일한 x축과 함께 좌표계를 나타낸다. 기준 프레임이 표준 구성에 있으므로, 두 관측자는 좌표계의 원점 위치에 동의한다. 움직이는 관찰자의 축은 서로 수직이 아니며 시간 축의 축척은 늘어난다. 특정 사건의 좌표를 결정하려면 두 축 중 하나에 각각 평행한 두 개의 선이 사건을 통과하여 생성되어야 하며, 축이 판독된 이들의 교차로도 생성되어야 한다.
다이어그램의 예로서 이벤트 A의 위치와 시간을 결정하면 예상대로 두 관측자가 동일한 시간을 갖게 된다. 위치 상이한 값에 대해서만, 움직이는 관찰자가 t = 0 이후 사건 A의 위치에 접근했기 때문에. 일반적으로, x축과 평행한 선상의 모든 사건은 두 관측자에 대해 동시에 일어난다. 하나의 공통 위치 축의 존재를 모델링하는 단 하나의 보편적 시간 t = t t가 있을 뿐이다. 반면에, 두 개의 다른 시간 축 때문에 관측자들은 보통 같은 사건에 대해 다른 좌표를 측정한다. x와 t에서 x와 t로, 그리고 그 반대의 이 그래픽 번역은 이른바 갈릴레이 변환에 의해 수학적으로 묘사된다.
민코프스키 도표
개요

민코우스키 도표라는 용어는 특수상대성이론에서 자주 사용되는 특정 형태의 스페이스타임 도표를 가리킨다. 민코프스키 도표는 밍코프스키 공간의 일부를 2차원 그래픽으로 표현한 것으로, 보통 공간이 하나의 차원으로 축소되었다. 이 다이어그램의 측정 단위는 사건 발생 시 라이트 콘이 해당 사건을 통과하는 경사 선 + 또는 마이너스 선으로 구성되도록 한다.[3] 수평선은 출발지에서 정지해 있는 관찰자에 대한 일반적인 동시 사건 개념에 해당한다.
특정한 민코프스키 도표는 로렌츠 변환의 결과를 보여준다. 로렌츠 변환은 두 개의 관성 기준 프레임과 관련되며, 여기서 이벤트(0, 0)에서 정지한 관찰자가 X축을 따라 속도를 변화시킨다. 으로서 그림에 나타나 2-1, 이전 시간 축과의 각도 α은 관찰자 형태의α<>.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .d과 함께 새로운 시간 축.En{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}π/4. 새로운 기준 틀에서 동시 발생은 이전의 동시성 선에 α로 기울어진 선과 평행하게 놓여 있다. 이것이 새로운 x축이다. 원래 축 세트와 프라이밍된 축 세트 모두 민코프스키 내측 제품 또는 상대론적 도트 제품과 관련하여 직교하는 속성을 가지고 있다.
α의 크기가 무엇이든 그림 2-2와 같이 선 ct = x는 범용[4] 이등분선을 형성한다.
밍코프스키 다이어그램과 자주 마주치게 되는데, 여기서 측정 시간 단위는 c 계수에 의해 크기가 조정되어 x의 한 단위는 t의 한 단위가 된다. 그러한 다이어그램은 다음과 같은 단위를 가질 수 있다.
이렇게 해서 광선은 축들 사이의 이등분선에 평행한 선으로 표현된다.
수학상세
x와 x x 축 사이의 각도 α는 시간 축 ct와 ct ct 사이의 각도 α와 동일할 것이다. 이는 특수 상대성 이론의 두 번째 추정에서 나온 것으로서, 빛의 속도는 상대적 움직임(아래 참조)에 관계없이 모든 관찰자에게 동일하다고 한다. 각도 α는 다음과[5] 같이 주어진다.
x와 t에서 x와 t에 해당하는 부스트와 그 반대의 부스트는 로렌츠 변환에 의해 수학적으로 설명되며, 이 변환은 기록할 수 있다.
여기서 =( 1 - 2)- / 2 }}은 로렌츠 계수다. 로렌츠 변환을 적용함으로써, 부스트 프레임에 대해 얻은 스페이스타임 축은 항상 하이퍼볼라 쌍의 결합 직경과 일치할 것이다. 그림 2-3과 같이, 부스트 및 부스트되지 않은 스페이스타임 축은 일반적으로 단위 길이가 같지 않다. U가 각각 ct와 x의 축의 단위 길이인 경우 ct와 x의 축의 단위 길이는 다음과 같다.[6]
ct축은 S에 놓여 있는 시계의 월드라인을 나타내며 U는 이 월드라인에서 일어나는 두 사건 사이의 지속시간을 나타내며, 이러한 사건들 사이의 적절한 시간이라고도 한다. X축의 길이 U는 S에 놓여 있는 로드의 나머지 길이 또는 적절한 길이를 나타낸다. S resting에 놓여 있는 시계와 로드의 ct--와 xax-ax의 거리 U′에도 동일한 해석을 적용할 수 있다.
역사
알버트 아인슈타인은 1905년에 특수 상대성을 발견했고,[7] 헤르만 민코프스키가 1908년에 그래픽으로 표현했다.[8]
민코프스키의 1908년 논문에는 세 개의 도표가 있었는데, 처음에는 로렌츠 변환을, 다음에는 라이트콘에 의한 비행기의 분할, 그리고 마지막으로 세계선의 삽화가 있었다.[8] 첫 번째 다이어그램은 하이퍼볼라 - 2= 단위의 분기를 사용하여 속도에 따라 적절한 시간 단위의 위치를 표시함으로써 시간 확장이 표시되었다. 두 번째 다이어그램은 공간을 보정하기 위한 공극 하이퍼볼라를 보여주었는데, 여기서 비슷한 스트레칭이 피츠제럴드 수축의 인상을 남긴다. 1914년에 루드윅 실버슈타인은[9] "로렌츠 변환의 미코프스키의 표현" 도표를 포함했다. 이 도표에는 단위 하이퍼볼라, 그 결합체 및 한 쌍의 결합 지름이 포함되었다. 1960년대 이후 이 보다 완전한 구성의 버전은 민코프스키 다이어그램으로 언급되어 왔으며, 특수상대성이론의 변환 기하학을 표준으로 나타낸 삽화로 사용되었다. E. T. 휘태커는 상대성 원리가 민코프스키 도표에서 시간적으로 하이퍼볼라 반경이 선택된 것의 중재성과 같다고 지적해 왔다. 1912년 길버트 N. 루이스와 에드윈 B. 윌슨은 민코프스키 도표가 있는 비유클리드 평면의 특성을 개발하기 위해 합성 기하학의 방법을 적용했다.[10][11]
테일러와 휠러가 스페이스타임 물리학(1966년)을 작곡할 때, 스페이스타임 기하학에는 '밍코프스키 도표'라는 용어를 쓰지 않았다. 대신에 그들은 민코프스키가 1908년의 혁신의 총체성에 의해 철학에 기여한 것을 인정하는 것을 포함했다.[12]
로에델 도표
민코프스키 다이어그램의 정지된 프레임은 직교 스페이스타임 축이 있는 반면, 민코프스키 다이어그램의 나머지 프레임에 상대적으로 움직이는 프레임은 스페이스타임 축이 있어 급성 각도를 형성한다. 특수 상대성 이론은 어떤 두 개의 관성 기준 프레임이 물리적으로 동등해야 한다고 가정하기 때문에 민코프스키 다이어그램의 이러한 비대칭성은 오해의 소지가 있다. 로에델 도표는 관성 기준 프레임의 대칭성을 훨씬 더 뚜렷하게 만드는 대체 스페이스타임 도표다.
중앙분리대 프레임을 통한 공식화
몇몇 저자들은 휴식 중인 것과 움직이는 것 사이에 대칭성이 뚜렷하게 나타날 ("중간 프레임")[13] 참조 프레임이 있다는 것을 보여주었다. 이 프레임에서 다른 두 프레임은 같은 속도로 반대 방향으로 움직이고 있다. 이러한 좌표를 사용하면 두 축의 길이와 시간의 단위가 동일해진다. β = v/c 및 β = 1/4201 - β가2 S과( S {\S^{\} 사이에 주어진 경우, 이러한 식은 다음과 같이 중위수 프레임 S의0 값과 연결된다.[13][14]
예를 들어, β = 0.S {\S}과 S {\ S} 사이에 있는 경우 (2) 각각 반대 방향으로 약 ±0.268c의 중앙 프레임0 S에서 이동한다. 반면 β0 = 0.5 in S인0 경우 (1) 자체 휴게 프레임에서 과 S S 사이의 상대 속도는 0.8c이다. 및 의 축 구성은 중위수 프레임의 직교 축과 관련하여 황갈색 α = β를0 사용하는 일반적인 방법에 따라 이루어진다(그림 3-1).
그러나 이러한 대칭도를 그릴 때는 중앙 프레임과 β를0 전혀 언급하지 않아도 다이어그램의 관계를 도출할 수 있는 것으로 나타났다. 대신 과() S 사이의 상대 속도 β = v/c 을(를) 다음 구성에서 직접 사용할 수 있어 동일한 결과를 제공할 수 있다.[15]
φ가 ct ct과 ct(또는 x와 x x 사이)의 축과 x′와 ct의 축 사이의 각도인 경우,[15][16][17][18] 다음과 같이 주어진다.
그림 3-2에서 볼 수 있는 두 가지 구성 방법은 다음과 같다: (a) x축은 ct′ 축에 수직으로 그려지고 x축과 ct-axes는 각도 φ에 추가되며, (b) x축은 ct′ 축에 대해 θ 각도로 그려지고, x축은 ct′ 축에 수직으로 추가된다.
민코프스키 다이어그램에서, 페이지의 길이는 민코프스키 다이어그램에서 축의 단위 길이 사이의 뒤틀림 계수 때문에 서로 직접 비교할 수 없다. 특히 민코스키 다이어그램에서 U과 U이(가) 각각 나머지 프레임 축과 이동 프레임 축의 단위 길이인 경우, 두 단위 길이는 다음 공식을 통해 서로 상대적으로 뒤틀린다.
대조적으로 대칭 로에델 도표에서 및 S 프레임 축은 모두 중위수 프레임에 상대적인 동일한 인수에 의해 뒤틀려져 있으므로 단위 길이가 동일하다. 이것은 Loedel 스페이스타임 다이어그램의 경우 페이지에 나타나는 여러 프레임 사이의 스페이스타임 길이를 직접 비교할 수 있음을 시사한다. Loedel 다이어그램의 대칭적 특성 때문에 프레임 간 단위 길이 스케일링/변환이 필요하지 않다.
역사
- Max Born(1920)은 2개의 로드와 2개의 시계가 반대 방향으로 움직이는 대칭 케이스에서 길이 수축과 시간 확장을 보여주기 위해 ct 축은 물론 x축에 거의 수직으로 위치시켜 민코프스키 도표를 그렸다.[19]
- 드미트리 미리마노프(1921)는 상대적으로 움직이는 두 프레임에 대해 항상 중앙분리대 프레임이 존재한다는 것을 보여주었고, 로렌츠 변환에서 그들 사이의 관계를 도출했다. 하지만 그는 도표로 그래픽으로 표현하지는 않았다.[13]
- 대칭 도표는 1921년 두 개의 논문에서 폴 그루너에 의해 요제프 사우터와 협력하여 체계적으로 개발되었다. 길이 수축과 시간 확장과 같은 상대론적 효과와 공변량 벡터 및 역변량 벡터와의 일부 관계가 그것들에 의해 입증되었다.[16][17] 그루너는 후속 논문(1922년-1924년)에서 이 방법을 연장했고, 미리마노프의 치료에도 공을 세웠다.[20][21][22][23][24][25]
- 대칭 민코프스키 다이어그램의 구성은 후에 여러 저자에 의해 독자적으로 재발견되었다. 예를 들어 1948년부터 엔리케 로에델 팔룸보는 스페인어로 된 일련의 논문을 발표하여 그러한 접근법의 세부사항을 제시하였다.[26][27] 1955년 앙리 아마르도 그러한 관계를 제시하는 논문을 발표하였고, 1957년 후속 논문에서 로에델에게 공을 돌렸다.[28][29] 교과서의 일부 저자들은 로에델 도표라고 하는 대칭 민코프스키 도표를 사용한다.[15][18]
도표에서의 상대론적 현상
시간확장
상대론적 시간 확장은 관찰자에 대해 움직이는 시계(휴게 프레임에 적절한 시간을 나타냄)가 더 느리게 작동하는 것으로 관찰되는 것을 말한다. 이 상황은 그림 4-1의 대칭 로에델 도표에 묘사되어 있다. 로에델 도표의 대칭적 특성 때문에 페이지 상의 스페이스타임 길이를 서로 직접 비교할 수 있다는 점에 유의하십시오.
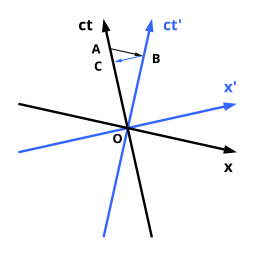
그림 4-2에서 검정색 축에 의해 기준 프레임이 주어지는 관찰자는 원점 O에서 A로 이동하는 것으로 가정한다. 이동 시계는 파란색 축에 의해 주어진 기준 프레임을 가지고 있으며, O에서 B로 이동한다. 흑인 관찰자의 경우, A에서 사건과 동시에 일어나는 모든 사건은 그 공간 축과 평행한 직선에 위치한다. 이 선은 A와 B를 통과하기 때문에 A와 B는 관찰자의 기준 프레임에서 검은색 축으로 동시에 이루어진다. 그러나 흑인 관찰자에 비해 움직이는 시계는 파란색 시간 축을 따라 오프 타임을 표시한다. 이것은 O에서 B까지의 거리로 표현된다. 따라서 검은색 축을 가진 A의 관찰자는 O에서 A까지의 거리를 읽는 동안 O에서 A까지의 거리를 읽는 것으로 시계를 알아차리고, O에서 B까지의 거리를 읽기 위해 시계가 움직이는 것을 관찰한다. 그들은 O에서 B까지의 거리가 O에서 A까지의 거리보다 작기 때문에, 그들 자신의 시계에서 지나간 시간보다 자신들과 비교해서 움직이는 시간이 더 작다고 결론짓는다.
O에서 B로 시계와 함께 이동한 두 번째 관찰자는 검은색 축 시계가 C에 도달했을 뿐이므로 더 느리게 작동한다고 주장할 것이다. 이러한 명백하게 역설적인 진술의 이유는 다른 장소에서 동시에 일어나는 사건들에 대한 다른 결정 때문이다. 상대성 원리 때문에 누가 옳으냐는 문제는 답이 없고 말이 안 된다.
길이 수축
상대론적 길이 수축은 관찰자에 대해 움직이는 지배자(휴게 프레임에서 적절한 길이를 나타냄)가 수축/단축되는 것을 관찰하는 것을 말한다. 상황은 그림 4-3의 대칭 로에델 도표에 묘사되어 있다. 로에델 도표의 대칭적 특성 때문에 페이지 상의 스페이스타임 길이를 서로 직접 비교할 수 있다는 점에 유의하십시오.
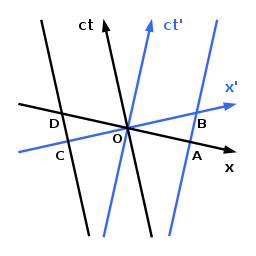
그림 4-4에서 관찰자는 ct 축을 따라 이동한다고 다시 가정한다. 그에 비례하여 움직이는 물체의 끝점의 세계선은 ct ct 축과 A와 B를 통과하는 평행선을 따라 이동하는 것으로 가정한다. 이 관찰자의 경우 t = 0에서 개체의 끝점은 O와 A이다. 물체와 함께 움직이는 두 번째 관찰자의 경우, 물체가 정지해 있도록, 물체는 t³ = 0에서 적절한 길이의 OB를 가진다. OA < OB. OB.는 OA < OB. 첫 번째 관찰자를 위해 물체가 수축된다.
두 번째 관찰자는 첫 번째 관찰자가 O와 A에서 각각 대상의 끝점을 평가했기 때문에 서로 다른 시간에 그 동안 그의 움직임으로 인해 잘못된 결과를 초래했다고 주장할 것이다. 두 번째 관찰자가 CT 축을 따라 이동하는 끝점과 C와 D를 통과하는 평행선을 가진 다른 물체의 길이를 조사하는 경우, 그는 OD에서 OC로 수축되는 것과 동일한 방법으로 결론을 내린다. 각 관찰자는 계약할 다른 관찰자와 함께 움직이는 물체를 추정한다. 이러한 명백한 역설적 상황은 다시 민코프스키 다이어그램을 통한 분석에서 입증된 동시성의 상대성 결과물이다.
이러한 모든 고려사항에서, 두 관측자는 이러한 사건이 발생하는 실제 시간을 결정하기 위해 그들이 보는 모든 사건과의 거리 및 빛의 속도를 고려한다고 가정했다.
빛의 속도의 항상성
특수상대성이론의 또 다른 가설은 빛의 속도의 항상성이다. 그것은 그들 자신에 대한 빛의 진공 속도를 측정하는 관성 기준 프레임에서 관찰자는 자신의 움직임과 광원의 움직임과 관계없이 동일한 값을 얻는다. 이 진술은 역설적으로 보이지만 이것을 산출하는 미분방정식에서 바로 따르며, 민코프스키 도표는 이에 동의한다. 그것은 또한 광자가 검출할 수 없는 매체를 통해 파동이라고 생각되었던 상대성 이론이 발견되기 전에는 미스터리로 여겨졌던 미셸슨-몰리 실험의 결과도 설명한다.
다른 방향으로 원점을 통과하는 광자의 세계 라인의 경우 x = ct 및 x = -ct hold. 즉, 그러한 세계선상의 어떤 위치도 동일한 절대값의 x축과 ct축에 대한 단계에 해당한다는 것을 의미한다. 축이 기울어진 좌표계의 좌표를 판독하는 규칙에서 두 개의 월드 라인은 x축과 ct축의 각도 이등분선이다. 그림 4-5와 같이, 민코프스키 도표는 그들을 x와 ct의 축의 각도 이등분자로 보여준다. 즉, 양쪽 관측자가 양쪽 광자에 대해 동일한 속도 c를 측정한다는 것을 의미한다.
임의의 속도로 관찰자에 해당하는 추가 좌표계를 이 민코프스키 도표에 추가할 수 있다. 이러한 모든 시스템에 대해 두 광자 월드 라인은 축의 각도 이등분선을 나타낸다. 상대 속도가 빛의 속도에 근접할수록 축은 해당 각도 이등분선에 접근한다. 축은 항상 광자 세계선보다 평탄하고 시간축은 더 가파르다. 두 축의 척도는 항상 동일하지만 대개 다른 좌표계의 척도와는 다르다.
빛의 속도 및 인과관계
두 광자 월드 라인보다 더 가파른 원점을 통과하는 직선은 빛의 속도보다 더 느리게 움직이는 물체와 일치한다. 만약 이것이 물체에 적용된다면, 이 광자의 세계선은 관성 기준 프레임에 대한 각도 이등분자이기 때문에 모든 관찰자의 관점에서 적용된다. 따라서 두 광자의 세계선 사이의 원점 위 어느 지점이라도 빛의 속도보다 작은 속도로 도달할 수 있고 원점과 인과 관계를 가질 수 있다. 이 영역은 절대적인 미래인데, 왜냐하면 어떤 사건이든 관찰자와 무관하게 원점으로 대표되는 사건과 비교했을 때 나중에 일어나기 때문인데, 그림 4-6의 민코스키 도표에서 그래픽으로 명백하다.
같은 주장을 따르는 경우, 출발지 아래의 범위와 광자 세계선 사이의 범위는 출발지에 상대적인 절대 과거가 된다. 그곳에서 일어나는 어떤 사건도 분명히 과거에 속하며, 그 기원에서의 영향의 원인이 될 수 있다.
모든 관측자에 대해 0보다 큰 시간 거리를 가지기 때문에 이러한 사건 쌍 사이의 관계를 시간 쌍이라고 한다. 이 두 사건을 연결하는 직선은 항상 같은 장소에서 일어나는 가능한 관찰자의 시간 축이다. 빛의 속도만으로 연결될 수 있는 두 가지 사건을 빛이라고 한다.
원칙적으로 3차원 표현으로 이어지는 민코프스키 다이어그램에 더 많은 차원의 공간을 추가할 수 있다. 이 경우 미래와 과거의 범위는 원점에서 정점이 서로 닿아 원뿔이 된다. 그것들은 가벼운 원추라고 불린다.
빛의 속도 제한
같은 논거에 따라 광자 세계선보다 수평에 가까운 원점을 통과하는 모든 직선은 관찰자의 속도에 관계없이 빛보다 빠르게 움직이는 물체나 신호에 대응하게 된다. 따라서 광원 바깥의 어떤 사건도 발원지로부터, 심지어 광신호에 의해서도, 빛의 속도 이하로 움직이는 어떤 물체나 신호로도 도달할 수 없다. 그러한 쌍의 사건들은 모든 관찰자에 대해 0과 다른 유한한 공간적 거리를 가지기 때문에 공간적 사건이라고 불린다. 한편, 그러한 사건들을 연결하는 직선은 항상 동시에 일어나는 가능한 관찰자의 공간 좌표 축이다. 양쪽 방향에서 이 좌표계의 속도를 약간 변화시키면 관측자가 이러한 사건의 연대순을 다르게 추정하는 관성 기준 프레임을 항상 찾을 수 있다.
그림 4-7의 O에서 A로 빠르게 움직이는 물체를 볼 때, 물체가 A에서 A로 이동하는 것을 지켜보는 관찰자의 경우, 물체가 A에서 O로 이동하는 다른 관찰자를 찾을 수 있다(첫 번째 관찰자에 대해서는 빛의 속도보다 작은 속도로 이동). 어느 관찰자가 옳은가에 대한 문제는 독특한 해답이 없고, 따라서 물리적인 의미가 없다. 그러한 움직이는 물체나 신호는 인과관계의 원리를 위반할 것이다.
또한, 빛보다 더 빠른 신호를 보내는 일반적인 기술적 수단은 정보가 발신자의 과거로 보내지는 것을 허용한다. 도표에서, x-ct 시스템의 O에 있는 관찰자는 빛보다 더 빠르게 움직이는 메시지를 A에게 보낸다. A에서 그것은 다른 관찰자에 의해 수신되고, 그것을 다시 빛보다 빠르게 되돌려 보내는 x′-ct′ 시스템에 있도록 움직이며, B에 도착한다. 그러나 B는 O에 비해 과거에 있다. 이 과정의 부조리는 두 관찰자가 나중에 그들이 전혀 메시지를 받지 않았음을 확인했을 때 명백해진다. 그러나 모든 메시지는 민코스키 도표에서 볼 수 있듯이 다른 관찰자를 향했다. 더욱이 관찰자를 빛의 속도로 가속시킬 수 있다면, 그들의 공간과 시간 축은 그들의 각도 이등분자와 일치할 것이다. 좌표계는 시간 확장으로 인해 시간이 효과적으로 그들을 위해 지나가는 것을 멈출 것이라는 사실과 일치하여 붕괴될 것이다.
이러한 고려사항들은 빛의 속도가 한계로서 스페이스타임의 특성의 결과물이며, 기술적으로 불완전한 우주선과 같은 물체의 특성의 결과가 아니라는 것을 보여준다. 그러므로 빛보다 빠른 움직임의 금지는 전자파나 빛과 특별히 관련이 없지만, 스페이스타임 구조의 결과로 온다.
관찰자 가속
특수상대성이 가속 입자 또는 가속 참조 프레임을 처리할 수 없다고 종종 부정확하게 주장한다. 실제로 가속입자는 특수상대성이론에서는 전혀 어려움이 없다. 반면에 가속 프레임은 어느 정도 특별한 치료가 필요하지만, 밍코우스키안 스팩타임을 다루는 한 특수상대성이 상황을 처리할 수 있다. 일반 상대성이 요구되는 것은 중력이 존재하는 경우에만이다.[30]
가속 입자의 4벡터 가속은 4폭의 적절한 시간에 관한 파생물이다. 이것은 다루기 어려운 상황이 아니다. 가속 프레임은 순간적으로 결합되는 기준 프레임(MCRF)의 개념을 이해하도록 요구한다. 즉, 주어진 순간 입자의 동일한 순간 속도로 이동하는 프레임이다.
그림 5-1의 애니메이션을 고려하십시오. 곡선은 양극 x 방향과 음극 x 방향의 방향의 완전한 변화를 포함하여 연속적인 가속을 거치는 입자의 세계선을 나타낸다. 빨간색 축은 입자의 궤적을 따라 각 지점에 대한 MCRF의 축이다. 프라이밍되지 않은(스테이션) 프레임의 이벤트 좌표는 로렌츠 변환을 사용하여 순간적으로 컴밍되는 프라이밍된 프레임의 좌표와 관련될 수 있다.
그림 5-2는 빠르게 가속하는 입자의 세계선을 따라 변화하는 스페이스타임의 관점을 보여준다. 축(그리지 않음)은 수직이고, x축(그리지 않음)은 수평이다. 점선은 입자의 시간 궤적("세계선")이다. 볼은 세계선을 따라 적절한 시간의 일정한 간격으로 배치된다. 단단한 대각선은 관찰자의 현재 사건에 대한 빛의 원뿔이며, 그들은 그 사건에서 교차한다. 작은 점들은 스페이스타임에 있는 다른 임의의 사건들이다.
세계선의 경사(수직선으로부터의 이탈)는 세계선의 그 구간에서 입자의 속도다. 세계선의 굴곡은 입자 가속을 나타낸다. 입자가 가속함에 따라, 그 입자의 스페이스타임에 대한 관점은 변한다. 이러한 관점의 변화는 로렌츠 변환의 지배를 받는다. 또한 다음 사항에 유의하십시오.
- 미래/후/과거 가속도 전/후/세계 라인의 공은 시간 확장으로 인해 더 간격을 두고 있다.
- 가속 전에 동시 발생했던 사건들(초기 간격 사건들)은 동시성의 상대성 때문에 이후 다른 시간에 있다.
- 이벤트는 적절한 시간의 진행으로 인해 라이트 콘 라인을 통과하지만 가속으로 인한 뷰의 변화 때문은 아니다.
- 세계선은 항상 현재 사건의 미래와 과거의 가벼운 원추 안에 남아있다.
만약 각 사건이 빛의 점멸이라고 상상한다면, 관찰자의 과거 광원 안에 있는 사건들은 관찰자가 볼 수 있는 사건들이다. 세계 선의 기울기(수직으로 인한 탈선)는 관찰자에 대한 상대적인 속도를 제공한다.
비삽입 기준 프레임의 경우
광자 월드 라인은 = 의 메트릭을 사용하여 결정된다[31] 광원뿔은 위치에 따라 변형된다. 관성 기준 프레임에서 자유 입자는 직선 세계 선을 가진다. 비삽입 기준 프레임에서 자유 입자의 월드 라인은 곡선이다.
로켓에서 초기 속도 없이 낙하한 물체의 낙하 예를 들어보자. 로켓은 관성 기준 프레임에 대해 균일하게 가속된 움직임을 가지고 있다. 비침습적 기준 프레임의 민코프스키 다이어그램의 그림 6-2에서 볼 수 있듯이, 물체는 한 번 떨어지고 속도가 빨라져 최대에 도달한 다음, 속도가 감소하고 적절한 시간이 에서 정지하는 수평선에서 무증상적으로 취소된다 그 속도는 가속 로켓에서 정지해 있는 관찰자에 의해 측정된다.
참고 항목
참조
- ^ "What are position vs. time graphs?". Khan Academy. Retrieved 19 November 2018.
- ^ Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (3rd ed.). Incomprehensible Books. ISBN 9780957389465.
- ^ 머민(1968년) 17장
- ^ 블라디미르 카라페토프 참조
- ^ Demtröder, Wolfgang (2016). Mechanics and Thermodynamics (illustrated ed.). Springer. pp. 92–93. ISBN 978-3-319-27877-3. 93페이지 추출
- ^ Freund, Jürgen (2008). Special Relativity for Beginners: A Textbook for Undergraduates. World Scientific. p. 49. ISBN 978-9812771599.
- ^ Einstein, Albert (1905). "Zur Elektrodynamik bewegter Körper" [On the electrodynamics of moving bodies] (PDF). Annalen der Physik. 322 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004.. 영어 번역도 참조하십시오.
- ^ a b Minkowski, Hermann (1909). [Space and time]. Physikalische Zeitschrift. 10: 75–88.
- 위키소스의 다양한 영어 번역 : 공간과 시간
- ^ Silberstein, Ludwik (1914). The Theory of Relativity. p. 131.
- ^ Wilson, Edwin B.; Lewis, Gilbert N. (1912). "The Space-time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics". Proceedings of the American Academy of Arts and Sciences. 48 (11): 387–507. doi:10.2307/20022840. JSTOR 20022840.
- ^ 윌슨과 루이스에 의해 사용된 공리와 이론의 요약인 합성 스페이시타임이 증명되었다. WebCite에 의해 보관됨
- ^ Taylor; Wheeler (1966). Spacetime Physics. p. 37.
Minkowski's insight is central to the understanding of the physical world. It focuses attention on those quantities, such as interval, which are the same in all frames of reference. It brings out the relative character of quantities, such as velocity, energy, time, distance, which depend on the frame of reference.
- ^ a b c Mirimanoff, Dmitry (1921). "La transformation de Lorentz-Einstein et le temps universel de M. Ed. Guillaume". Archives des sciences physiques et naturelles (Supplement). 5. 3: 46–48. (번역: 로렌츠-아인슈타인 변환과 에드 보편적 시간. 기욤)
- ^ Shadowitz, Albert (2012). The Electromagnetic Field (Reprint of 1975 ed.). Courier Dover Publications. p. 460. ISBN 978-0486132013. 460페이지의 Google 책 보기
- ^ a b c Sartori, Leo (1996). Understanding Relativity: A simplified approach to Einstein's theories. University of California Press. pp. 151ff. ISBN 0-520-20029-2.
- ^ a b Gruner, Paul; Sauter, Josef (1921). "Représentation géométrique élémentaire des formules de la théorie de la relativité" [Elementary geometric representation of the formulae of the theory of relativity]. Archives des sciences physiques et naturelles. 5. 3: 295–296. (번역: 특수 상대성 이론의 공식에 대한 기초 기하학적 표현)
- ^ a b Gruner, Paul (1921). "Eine elementare geometrische Darstellung der Transformationsformeln der speziellen Relativitätstheorie" [An elementary geometric representation of the transformation formulae of the special theory of relativity]. Physikalische Zeitschrift. 22: 384–385. (번역: 특수 상대성 이론의 변환 공식에 대한 기초 기하학적 표현)
- ^ a b Shadowitz, Albert (1988). Special Relativity (Reprint of 1968 ed.). Courier Dover Publications. pp. 20–22. ISBN 0-486-65743-4.
- ^ Born, Max (1920). Die Relativitätstheorie Einsteins [Einstein's Theory of Relativity]. Naturwissenschaftliche monographien und lehrbücher ... 3. Bd. (First ed.). Springer. pp. 177–180. Google 서적 제3판(1922년)의 재인쇄(2013년) 페이지 187을 참조하십시오.
- ^ Gruner, Paul (1922). Elemente der Relativitätstheorie [Elements of the theory of relativity]. Bern: P. Haupt.
- ^ Gruner, Paul (1922). "Graphische Darstellung der speziellen Relativitätstheorie in der vierdimensionalen Raum-Zeit-Welt I" [Graphical representation of the special theory of relativity in the four-dimensional spacetime world I]. Zeitschrift für Physik. 10 (1): 22–37. Bibcode:1922ZPhy...10...22G. doi:10.1007/BF01332542. S2CID 123131527.
- ^ Gruner, Paul (1922). "Graphische Darstellung der speziellen Relativitätstheorie in der vierdimensionalen Raum-Zeit-Welt II" [Graphical representation of the special theory of relativity in the four-dimensional spacetime world II]. Zeitschrift für Physik. 10 (1): 227–235. Bibcode:1922ZPhy...10..227G. doi:10.1007/BF01332563. S2CID 186220809.
- ^ 그뤼너, 폴(1921년)."a)Représentation graphique 드 l'univers espace-temps. 4차원 à b)Représentation graphique(temps universel dans 라 théorie 드 라 relativité"[보편적인 시간의 상대성 이론의 4차원 우주의 a)도해적 표현입니다. b)전계도].기록 보관소. 5.4:234–236.(번역:4차원의 시-공간 우주의 도해적 표현)과학 이런(naturelles des.
- ^ Gruner, Paul (1922). "Die Bedeutung "reduzierter" orthogonaler Koordinatensysteme für die Tensoranalysis und die spezielle Relativitätstheorie" [The importance of "reduced" orthogonal coordinate-systems for tensor analysis and the special theory of relativity]. Zeitschrift für Physik. 10 (1): 236–242. Bibcode:1922ZPhy...10..236G. doi:10.1007/BF01332564. S2CID 120593068.
- ^ Gruner, Paul (1924). "Geometrische Darstellungen der speziellen Relativitätstheorie, insbesondere des elektromagnetischen Feldes bewegter Körper" [Geometrich representations of the special theory of relativity, in particular the electromagnetic field of moving bodies]. Zeitschrift für Physik. 21 (1): 366–371. Bibcode:1924ZPhy...21..366G. doi:10.1007/BF01328285. S2CID 121376032.
- ^ Loedel, Enrique (1948). "Aberración y Relatividad" [Aberration and Relativity]. Anales de la Sociedad Cientifica Argentina. 145: 3–13.
- ^ 피시카상대비스타, 아르헨티나 부에노스 아이레스의 카펠루즈 편집장(1955년).
- ^ Amar, Henri (1955). "New Geometric Representation of the Lorentz Transformation". American Journal of Physics. 23 (8): 487–489. Bibcode:1955AmJPh..23..487A. doi:10.1119/1.1934074.
- ^ Amar, Henri; Loedel, Enrique (1957). "Geometric Representation of the Lorentz Transformation". American Journal of Physics. 25 (5): 326–327. Bibcode:1957AmJPh..25..326A. doi:10.1119/1.1934453.
- ^ Gibbs, Philip. "Can Special Relativity Handle Acceleration?". The Original Usenet Physics FAQ. University of California, Riverside. Retrieved 6 November 2021.
- ^ Mathieu Rouaud (2020). Special Relativity, A Geometric Approach (PDF). p. 534. ISBN 978-2-9549309-3-0.
- 앤서니 프랑스어 (1968년) 특수 상대성, 페이지 82 & 83, 뉴욕: W W 노턴 & 컴퍼니.
- E.N. Glass(1975) "로렌츠 부스트와 민코스키 도표" 미국 물리학 저널 43장 1013,4.
- N. David Mermin(1968) 특수상대성이론에서의 공간과 시간, 17장 민코프스키 도표: Spacetime의 기하학, 155-99 맥그로우 힐.
- Rindler, Wolfgang (2001). Relativity: Special, General and Cosmological. Oxford University Press. ISBN 0-19-850836-0.
- W.G.V. 로서(1964) 상대성 이론 소개, 256페이지, 그림 6.4, 런던: 버터워스.
- 에드윈 F. Taylor와 John Archibald Wheeler(1963) Spacetime Physics, 페이지 27~38, 뉴욕: W. H. Freeman and Company, Second Edition(1992년).
- Walter, Scott (1999), "The non-Euclidean style of Minkowskian relativity" (PDF), in J. Gray (ed.), The Symbolic Universe: Geometry and Physics, Oxford University Press, pp. 91–127 (e-링크 10페이지 참조)
외부 링크
![]() 위키미디어 커먼스의 민코프스키 다이어그램 관련 매체
위키미디어 커먼스의 민코프스키 다이어그램 관련 매체












 (
(


 (가) 각각 나머지 프레임 축과 이동 프레임 축의 단위 길이인
(가) 각각 나머지 프레임 축과 이동 프레임 축의 단위 길이인