연속 시간 마르코프 연쇄

연속시간 마르코프 연쇄(CTMC)는 각 상태에 대해 프로세스가 지수 랜덤 변수에 따라 상태를 변화시킨 후 확률행렬의 확률에 의해 지정된 다른 상태로 이동하는 연속 확률 과정이다.등가 공식은 프로세스가 이동할 수 있는 각 가능한 상태에 대해 하나씩, 현재 상태에 의해 결정되는 파라미터와 함께 일련의 지수 랜덤 변수의 최소값에 따라 변화하는 상태를 기술한다.

3가지 상태 $\{0,1,2\}$ , 2 ${\displaystyle$ \{ $0,1,$ 2\}을 $\{0,1,2\}$ 가진 CTMC의 예는 다음과 같습니다.이 프로세스는 유지시간에 의해 지정된 시간(지수 랜덤 $E_{i}$ i\ $displaystyle E_{i$ 후에 이행합니다.여기서 i는 현재 상태입니다.각 랜덤 변수는 독립적이며 $E_{0}\sim {\text{Exp}}(6)$ 0 $E_{0}\sim {\text{Exp}}(6)$ ~ $E_{0}\sim {\text{Exp}}(6)$ ( $E_{0}\sim {\text{Exp}}(6)$ ) $E_{0}\sim {\text{Exp}}(6)$ { $displaystyle E_{0}$ \ $sim$ { $text$ } $E_{1}\sim {\text{Exp}}(12)$ $}}(6$ $E_{1}\sim {\text{Exp}}(12)$ (12 $E_{1}\sim {\text{Exp}}(12)$ {\ $displaystyle E_{1}\sim {text}$ $Exp}}(12)$ $E_{2}\sim {\text{Exp}}(18)$ $E_{2}\sim {\text{Exp}}(18)$ ( $)$ {\ $displaystyle E_{2}\$ sim {text $}$ Exp $}}(18$ 이행이 이루어지는 경우 프로세스는 확률행렬을 가진 이산시간 마르코프 연쇄인 점프 체인에 따라 $이동$ 한다.

{\frac {1}{2}}\{\frac {1}{3}}\{\frac {5}{6}}\{\frac {1}{6}&{\frac {1}{2}{3}}&{\frac {1}{6}}&{\end{bmatrix}}}.

마찬가지로 이 CTMC는 서로 경쟁하는 지수의 이론에 따라 $E_{i,j}\sim {\text{Exp}}(q_{i,j})$ ~ $E_{i,j}\sim {\text{Exp}}(q_{i,j})$ ( $E_{i,j}\sim {\text{Exp}}(q_{i,j})$ i $E_{i,j}\sim {\text{Exp}}(q_{i,j})$ $)\displaystyle E_{i,j}\sim{$ text $}$ 의 최소 2개의 랜덤 변수에 따라 상태를 변경합니다. $Exp}}(q_{i,j}($ $i\neq j$ )는 i $i\neq j$ { $displaystyle$ i $\neq$ j ）。여기서 파라미터는 Q $Q=(q_{i,j})$ ( $Q=(q_{i,j})$ , $Q=(q_{i,j})$ j ) { $displaystyle$ Q = ( $q _$ { $i$ , j ) } 。

(\displaystyle {bmatrix}-6&3&3&3&12&8\15&3&18\end{bmatrix})}

각 비대각값은 점프 체인에서 소정 상태로 이동할 확률로 원상태 유지시간의 곱으로 계산할 수 있다.대각 값은 각 행의 합계가 0이 되도록 선택됩니다.

CTMC는 지수분포와 이산시간 마르코프 사슬의 기억불량 때문에 그 행동이 현재의 상태에만 의존하며 과거의 행동에 의존하지 않는다는 마르코프 속성을 만족시킨다.

정의.

$(\Omega ,{\cal {A}},\Pr )$ , $(\Omega ,{\cal {A}},\Pr )$ $(\Omega ,{\cal {A}},\Pr )$ {\ $displaystyle$ $(\Omega ,{\cal {A}},\Pr )$ (\ $Omega, {\cal$ { $A}},\$ Pr $})$ 을 ${\displaystyle(\Omega,{\cal {A},\Pr})}$ 확률 공간,S {\ $displaystyle$ S $}$ 를 $s$ 공란이 아닌 집합, T $=$ $T=\mathbb {R} _{\geq 0}$ $T=\mathbb {R} _{\geq 0}$ 0 {\ $displaystyle$ T=\ $mathbbb {R}_{\geq$ } $T=\mathbb {R} _{\geq 0}$ $Tstyle$ }로 $t$ $T=\mathbb {R} _{\geq 0}$ . $displaystyle$ S $)$ 에 $s$ 이산 메트릭을 장착하여 $함수$ R { 0 $\mathbb {R} _{\geq 0}\to S$ S(\displaystyle \mathbb {R} _ ${\geq$ 0 $}\to$ S $\mathbb {R} _{\geq 0}\to S$ 의 올바른 연속성을 이해할 수 있도록 $합니다$ . 연속 시간 마르코프 체인은 다음과 ^[1]같이 정의됩니다.

S ${\displaystyle$ S $}$ 의 $\lambda$ 확률 벡터 $\lambda$ { $displaystyle \lambda}($ 아래에서는 마르코프 체인의 초기 분포로 해석합니다) 및
S ${\displaystyle$ S $S$ 의 $Q$ 속도 $행렬$ Q{\ $displaystyle$ Q}, 즉 $Q:S^{2}\to \mathbb {R}$ Q: $Q:S^{2}\to \mathbb {R}$ 2 $Q:S^{2}\to \mathbb {R}$ {\ $displaystyle$ Q $:$ $S^{2}\to \mathbb {R} }$ 은 $Q:S^{2}\to \mathbb {R}$ 다음과 같습니다.

모든 $i,j\in S,0\leq Q_{i,j}$ i $i,j\in S,0\leq Q_{i,j}$ $i,j\in S,0\leq Q_{i,j}$ S $i,j\in S,0\leq Q_{i,j}$ $i,j\in S,0\leq Q_{i,j}$ $i,j\in S,0\leq Q_{i,j}$ \ $displaystyle$ i $, j\in$ S, $0\leq Q_{i,j$
모든 $i\in S,$ S $,$ {\ $style$ i $\in$ S $,}$ $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ j $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ : j $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ , $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ - $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ i , $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ . $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ { $displaystyle \sum$ _ { $j$ \ $in$ I : $j$ \ $neq$ i } $Q _$ { i , j $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ = - $Q _$ { $i$ , i $\sum _{j\in I:j\neq i}Q_{i,j}=-Q_{i,i}.$ } (이것이 $I$ $무한정 스타일$ 인 $I$ 에도 $)$ 예시의사후적으로는 합계가 유한해야 한다는 것을 알고 $있습니다$ (+ ${\$ (\displaystyle $+\infty)).$ $-Q_{i,i}$ , $(\$ i})와 $-Q_{i,i}$ 동일하다고 가정하고 Q $(\displaystyle$ -Q_{ $i,$ i $-Q_{i,i}$ })가 $Q$ 실제 가치라고 $Q$ 합니다.대신 일부 저자는 $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$ 된 규정 $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$ : $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$ $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$ $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$ R $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$ { - $}$ { - } { $display$ Q $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$ : $S^{2}\to \mathbb$ $\operatorname {range} Q\subseteq \mathbb {R}$ { $R}$ \ $cup \{-\infty$ $Q$ 를 들어Q(\ $displaystyle$ Q $\operatorname {range} Q\subseteq \mathbb {R}$ 는 $Q$ 안정적이거나 $\operatorname {range} Q\subseteq \mathbb {R}$ 안정되어 $,$ Q(\ $displaystyle \operatorname {range} Q\subseteq \mathbbb$ {R} $\operatorname {range} Q\subseteq \mathbb {R}$ 즉 모든 엔트리가 실제 값입니다).^[2]^[3]^[4]

Q $({display$ Q $})$ 의 $Q$ 행 합계는 0: $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ ∑ j $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ i , $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ $\forall i\in S~\sum _{j\in I}Q_{i,j}=0,$ 0 , { $display$ style \ $forall$ i \ $in$ S ~ \ $sum$ _ { $j$ \ $in$ I } $Q_{ i$ , j } $Q\cdot 1=0$ $0$ , $Q\cdot 1=0$ more more $Q\cdot 1=0$ = 0 $CDot style$ 입니다.이 상황은 전이행렬의 모든 행 합계가 동일한 이산 시간 마르코프 사슬의 상황과 대조된다.

$X:T\to S^{\Omega }$ X $X:T\to S^{\Omega }$ : $X:T\to S^{\Omega }$ $X:T\to S^{\Omega }$ $X:T\to S^{\Omega }$ \ $displaystyle$ X : $({\cal {A}},{\cal {P}}S)$ $\$ T $X:T\to S^{\Omega }$ X ( t ) $X:T\to S^{\Omega }$ { $display$ \ $forall$ t ~ $in T$ ~ X $\forall t\in T~X(t)$ ( $t$ ) $\forall t\in T~X(t)$ $({\cal {A}},{\cal {P}}S)$ { $display$ style ( \ $cal$ { $A$ } , { \ $cal$ { $P } )$ } - 측정 $({\cal {A}},{\cal {P}}S)$ 가능.X $({displaystyle$ X})를 $X$ 초기 분포 $\lambda$ $x$ (\ $displaystyle \lambda)$ 및 $\lambda$ 속도 $행렬$ Q(\ $displaystyle$ Q $Q$ 전이 확률 또는 점프 체인 및 유지 시간을 ^[5]통해 마르코프라고 정의하는 세 가지 동등한 방법이 있습니다.

전이 확률 정의의 서막으로서, 우선 정규 속도 매트릭스의 정의에 동기를 부여한다.우리는 전이율 행렬Q(\ $displaystyle$ Q $)$ 를 $Q$ 사용하여 다음 정리를 통해S $(\displaystyle$ S $)$ 에 전이 $P(t)$ P $(\$ $displaystyle P(t$ $))$ 컬렉션을 생성하여 마르코프 체인의 역학을 지정한다 $t\in \mathbb {R} _{\geq 0}$

정리: 콜모고로프 ^[6]역방정식에 대한 솔루션의 존재. : P $P\in ([0,1]^{S\times S})^{T}$ ( [ 0 $P\in ([0,1]^{S\times S})^{T}$ , $P\in ([0,1]^{S\times S})^{T}$ ] $P\in ([0,1]^{S\times S})^{T}$ $P\in ([0,1]^{S\times S})^{T}$ ) $P\in ([0,1]^{S\times S})^{T}$ \ $display style$ P \ $in$ ( [ $0$ , $1$ ]^ 가 $P\in ([0,1]^{S\times S})^{T}$ 합니다. ${S\times S}^{$ $T}}:$ $i,j\in S$ i $i,j\in S$ $i,j\in S$ S $(\displaystyle$ i $,j\in$ S $)$ 에 $i,j\in S$ 대해 엔트리 $P$ $(P(t)_{i,j})_{t\in T}$ ) $,$ $(P(t)_{i,j})_{t\in T}$ T $(\displaystyle$ (P $(t)_{i,$ j})_{t\ $in$ T})는 $(P(t)_{i,j})_{t\in T}$ 미분 가능하며 $P$ (\ $displaystyle$ P $)$ 는 $P$ 콜모고로프의 역방정식을 만족합니다.

P(0)=([i=j])_{i,j\in S},~\forall t\in T~\forall i,j\in S~~(P(t)_{i,j}'=\sum _{k\in S}Q_{i,k}P(t)_{k,j}.

(0)

$Q($ 표시 스타일 $Q)$ 는 $Q$ 위의 시스템에 고유성이 있음을 의미하며,^[7]^[8] 즉 솔루션이 하나밖에 없다는 것을 의미합니다.Q $(디스플레이 스타일$ Q $)$ 가 $Q$ 불규칙하다는 $Q$ 은 Q $(디스플레이 스타일$ Q $)$ 가 $Q$ 정규적이지 않다는 것을 $Q$ 합니다.S $(\displaystyle$ S $)$ 가 $S$ 유한한 $경우$ , P $P=(e^{tQ})_{t\in T},$ ( $P=(e^{tQ})_{t\in T},$ t $P=(e^{tQ})_{t\in T},$ Q ) $P=(e^{tQ})_{t\in T},$ T $,$ {\ $displaystyle$ P= ( $e^{tQ)_{t\in$ T $},$ 즉 $P=(e^{tQ})_{t\in T},$ $(\displaystyle$ Q $)$ 의 $Q$ 해는 정확히 1개입니다.그렇지 않으면, S{S\displaystyle}, 그리고 만약 Q{Q\displaystyle}일반이 불규칙한 전이율 매트릭스 S{S\displaystyle}에 .[를]는 고유한 방법 P{P\displaystyle}, 각 t∈ T{\displaystyle t\in T}을 위해, P(t){P(t)\displaystyle}가 될 것이다 확률 행렬:각 행의 존재하는 무한하다..[6]Q $(\displaystyle$ Q $)$ 는 $Q$ 다음 서브섹션의 시작부터 이 섹션의 끝부분까지 $Q$ 이라고 가정합니다.단, 이 전제조건을 포함하지 않는 것이^[10]^[11]^[12] 일반적입니다.(전문가의 주의: 따라서 우리는 일반적으로 연속 시간 마르코프 사슬을 정의하는 것이 아니라 비폭발적 연속 시간 마르코프 사슬만을 정의하는 것이다.)

전이 확률 정의

P $(\displaystyle$ P $)$ 를 $P$ 시스템(0)의 (고유) 솔루션으로 $합니다$ .(Q $(\displaystyle$ Q $)$ 는 $Q$ $Q$ 이라는 가정 하에 고유성이 보증됩니다.)우리는 X{X\displaystyle}은 마르코프 초기 분배와 λ{\lambda\displaystyle}과 비율 매트릭스 Q{Q\displaystyle}를 의미하는 것:모든 실수가 음이 아닌 정수 n, 모든 t0,…을 tn+0{\displaystyle n\geq 0}≥ 1∈ T{\displaystyle t_{0},\dots T}가 t0<>⋯<>,t_{n+1}\in;기 위해서는 말한다n+ $t_{0}<\dots <t_{n+1},$ 1 $t_{0}<\dots <t_{n+1},$ $i_{0},\dots ,i_{n+1}\in I,$ i0 $i_{0},\dots ,i_{n+1}\in I,$ $i_{0},\dots ,i_{n+1}\in I,$ + $i_{0},\dots ,i_{n+1}\in I,$ $i_{0},\dots ,i_{n+1}\in I,$ $,$ {\ $displaystyle$ i_0}, $\dots, i_{n+$ 1}\ $in$ I $,}$ 에 $t_{0}<\dots <t_{n+1},$ 대해 {\displaystyle $t_{$ $0}$ $t_{0}<\dots <t_{n+1},$ <\ $dots$ < $t_{$ $n$ +1}

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

(

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

0

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

0 ,

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

,

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

t

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

+

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

+

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

)

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

i

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

k

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

Z :

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

k <

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

P (

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

+

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

-

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

)

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

k ,

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

k +

\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k<n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}

( \

display

style \

Pr

( X

_

0 =

i _

0 ,

dots

, X _

1

\ dots , 1 ) = {

1

} {

n

}

(1)

유도 및 $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ A $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ Pr ( $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ ) $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ 0 $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ ( A $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ B ) $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ ( $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ B ) $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ ( $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ ) , $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ \ $display$ style \ $forall$ A , B \ $in$ \ $cal$ { $A$ } ~\ $neQ$ \ $Right$ （ A b B ）。))나는}과 비음의 정수 n, 모든 t0,…을 tn+0{\displaystyle n\geq 0}≥ 1∈ T{\displaystyle t_{0},\dots}T가 t0<>,t_{n+1}\in, ⋯<>t n+1,{\displaystyle t_{0}<, \dots <, t_{n+1},}{\displaystyle i\in I,~\Pr(X_{0}일 경우 =i)=\lambda_{나는}λ에 대한 모든 나는 0,…, i. n+1∈ 나는 $i_{0},\dots ,i_{n+1}\in I$ $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ < $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ ( $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ $i_{0},\dots ,i_{n+1}\in I$ $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ 0 , $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ , $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ t $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ n ){ $display$ 0 < \ $Pr$ ( X $_$ { 0 } = i _ $0 ,$ \ $dots$ , $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ _ { t _ { n } = $i_{$ $0<\Pr(X_{t_{n}}=i_{n})$ }\ $in$ I $i_{0},\dots ,i_{n+1}\in I$ ）。 ( $0<\Pr(X_{t_{n}}=i_{n})$ 뒤에 $0<\Pr(X_{t_{n}}=i_{n})$ X _ { $t$ _ { n $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ $0<\Pr(X_{t_{n}}=i_{n})$ )

\Pr(X_{t_{n+1})=i_{n+1}\mid X_{t_{n}=i_{n},\dots,X_{t_{0}=i_{0}=P(t_{n+1})_i_{n}.}

(2)

함수 $(P(t)_{i,j})_{t\in T}$ $(P(t)_{i,j})_{t\in T}$ ( $(P(t)_{i,j})_{t\in T}$ ) $(P(t)_{i,j})_{t\in T}$ , $(P(t)_{i,j})_{t\in T}$ j ) $(P(t)_{i,j})_{t\in T}$ T { $displaystyle$ ( P ( $t$ ) _ { $i$ , j $} _$ { $t$ \ $in$ T $(P(t)_{i,j})_{t\in T}$ } ( $i,j\in S$ i , $i,j\in S$ S \ $displaystyle$ i , $j$ \ $in$ S $i,j\in S$ )의 연속성에 따라 궤적 $(X_{t}(\omega ))_{t\in T}$ $(X_{t}(\omega ))_{t\in T}$ ( $(X_{t}(\omega ))_{t\in T}$ ) t $(X_{t}(\omega ))_{t\in T}$ T $(X_{t}(\omega ))_{t\in T}$ $displaystyle$ ( \ displaystyle i , j \ in S )가 $됩니다.$ $isplaystyle$ S $):$ $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ $displaystyle \Pr }$ -null $\Pr$ $집합N$ { $displaystyle$ N $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ ( X $\Pr$ $N$ ( $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ ) $t$ T $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ right continuous $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ } ${\$ N { displaystyle \ { \ { \ $in$ \ $Omega$ : ( \ t ) } ( X $t$ ) $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ ） $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ T n T n n n n n n n n continu continu n $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$ n continu continu continu continu continu continu continu continu continu continu continu continu continu continu continu continu continu continu continu 、 N \ $display$ styledisplay

점프 체인/홀딩 타임 정의

오른쪽 연속 함수와 연관된 시퀀스

$f:T\to S$ $f:T\to S$ T $f:T\to S$ \ $displaystyle$ f $:$ T $\to$ S는 $f:T\to S$ 오른쪽 연속입니다( $S$ $\displaystyle$ S에 이산 $S$ 메트릭을 $S$ 하는 경우). $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ( $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ f ) $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ( $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ { $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ( $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ , + $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ u $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ) : $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ( $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ + $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ) $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ( $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ ) $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ } $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ T ) { $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ { $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ + 、 0 $h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$ 、 { $display$ h = h ( f ) $=$ ( \ $inf$ \ \ \ \ \ \ infty ) $f$ + $u$ \ u \ （ t ) f _ （ t （ t （ t ）） f （ t （ t ）f{\ $displaystyle$ f $f$ 에 연관된 시간 시퀀스를 선택하고 s $s\in S,$ S $s\in S,$ , \ $displaystyle$ s \ $in$ S , $s\in S,$ } 를 $s\in S,$ $s\in S,$ 합니다.

y=y(f)=\leftparam\cases}f(\sum _{k\in n}H_{k}인 경우}&{\text{k}H_{k}<+\infty},\s&{\text{cases}\right}})_{n\in\in\cases}}}

f $\displaystyle$ f와 $f$ 된 "상태 시퀀스"입니다.

점프 매트릭스 δ의 정의

Q $(\displaystyle$ $Q$ $Q$ 에 $대한$ 의존성을 강조하려면 점프 $\Pi$ $(\displaystyle$ \Pi $)$ 가 $\Pi (Q)$ 매트릭스입니다.

\displaystyle \Pi =([i=j])_{i\in Z,j\in S}\cup \bigcup _{i\in S\setminus Z}({(i,j),-Q_{i,i}):j\in S\setminus \{i\}\cup \{(i,0}),

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

서 Z

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

(

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

)

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

{

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

S :

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

,

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

}

{

displaystyle

Z

=Z(Q

)=\{

k\in

S

:

Q_{k,k}=0\}

은

Z=Z(Q)=\{k\in S:Q_{k,k}=0\}

함수

(Q_{k,k})_{k\in S}.

k ,

(Q_{k,k})_{k\in S}.

)

(Q_{k,k})_{k\in S}.

S . {

displaystyle (Q_{k,k)}_{k\in

S

})

의 제로 세트입니다.

점프 체인/홀드 타임 속성

X $({displaystyle$ X $})$ 는 $X$ 초기 분포 $\lambda$ {\({ $displaystyle \lambda})$ 와 $\lambda$ 레이트 $매트릭스$ Q({ $displaystyle$ Q})를 $Q$ 갖는 마르코프라고 $합니다$ . 즉 $,$ X({ $displaystyle$ X})의 $X$ 궤적은 거의 확실하게 연속적이므로 f $({$ $displaystyle$ f $})$ 를 X $($ 어디에나)를 $X$ 수정한 $f$ 입니다.- 연속 궤적, $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ n $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ Z $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ H ( $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ ( $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ ) n $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ + ${\$ { $displaystyle \sum$ _ { $n\in \mathbb$ { $Z$ } $_$ { \ $geq$ 0 $}H$ ( $f$ ( \ $메가$ ) _ { n } _ { n } = + \ in \ $in$ ftfty $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ } } surely $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ ( surely surely surely surely surely $surely$ surely surely surely surely surely surely surely surely surely the surely surely surely surely surely surely the surely surely the $surelystyle$ surely the thestyle the $X$ surely surelystyle $、$ X - 。초기 분포 rkov 체인 ${\$ { $\lambda$ \ $lamb$ $display$ - chain property $\Pi (Q),$ $}$ $\lambda$ trans trans transition trans $\Pi (Q),$ r $\Pi (Q),$ r r \ $Pi$ ( $Q$ ) $\Pi (Q),$ $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ n $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ 0 $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ R $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ 0 $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ ） $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ ( $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ ( f $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ ) $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ ) $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ - Q $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ ) $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-Q_{Y_{n},Y_{n}})(B)$ {\ $cal {B}({\geq$ 0 $})~\Pr(H_{n}(f)\in$ B $)=\operatorname {Exp}(-Q_{Y_{n},Y_{n})(B)}($ 유지시간 속성 $).$

극소 정의

연속 시간 마르코프 사슬은 상태 i와 j 사이의 전이 확률의 시간에 대한 도함수인 전이율에 의해 특징지어진다.

X $(\displaystyle$ X $)$ 는 $X$ $\lambda$ 초기 분포 ${\(\displaystyle \displayda)$ 와 속도 $행렬$ Q(\ $displaystyle$ Q $)$ 를 $Q$ 가진 마르코프라고 $합니다$ . 즉, $i\in S,$ i $\Pr(X(0)=i)=\lambda _{i}$ $i\in S,$ S $,$ {\ $displaystyle$ i $\$ $in$ S $,}$ $\Pr(X(0)=i)=\lambda _{i}$ $i\in S,$ $($ ( $0$ ) $= i$ ) $\Pr(X(0)=i)=\lambda _{i}$ $\Pr(X(0)=i)=\lambda _{i}$ = $lami$ _dai를 $의미$ 합니다. $displaystyle$ t $}$ 및 $t$ h{\ $displaystyle$ h $h$ 의 작은 양의 값에 대해서는 0 $0<\Pr(X(t)=i)$ < $0<\Pr(X(t)=i)$ ( $0<\Pr(X(t)=i)$ ( $0<\Pr(X(t)=i)$ ) $0<\Pr(X(t)=i)$ ) \ $displaystyle$ 0 < \ $Pr$ ( $X$ ( t ) = $i$ 과 같은 모든 $t\in T$ $t\in T$ { $displaystyle$ t \ $in$ T $t\in T$ }에 $t\in T$ 대해 다음 값이 유지됩니다.

=

=[i=

j]+

Q_{i,j}h+o(

h

\Pr(X(t+h)=j\mid X(t)=i)=[i=j]+Q_{i,j}h+o(h)

여기서 little-o $o(h)$ o( $)$ { $displaystyle$ o( $h)}$ 는 $o(h)$ i $,$ $j, h$ { $displaystyle$ i $,j,h$ ^[15]^[16]에 따라 달라집니다.

위의 방정식은 $q_{ij}$ i $($ ij})가 $q_{ij}$ i $(\$ display $i$ style i $\$ neq $j$ $i\neq j$ j $i\neq j$ 에서 j $(\$ $display style$ i $\neq$ j)로 이행하는 속도와 i $= j$ (\ $display style$ i $\$ neq j $)$ 에서 $i$ $i$ 하는 속도를 측정하는 것으로 볼 수 있습니다. $i=j$ 를 클릭합니다.

특성.

커뮤니케이션 클래스

통신 클래스, 전이, 재발 및 정의 및 늘 반복은 이산 시간 마르코프 사슬과 동일하게 정의된다.

일시적인 동작

항목이_ij p = P(X_t = j X₀ = i)인 행렬에 P(t)를 씁니다.그러면 행렬 P(t)는 1차 미분 방정식인 순방향 방정식을 만족한다.

P'(t)=P(t)Q

여기서 prime은 t에 대한 차이를 나타낸다.이 방정식의 해는 행렬 지수함수에 의해 주어진다.

P(t)=e^{tQ}

상태 공간 {1,2}의 CTMC와 같은 단순한 경우.이러한 과정의 일반 Q 행렬은 α,β > 0인 다음 2 × 2 행렬이다.

({displaystyle Q=begin{pmatrix}-\alpha &\alpha &-\alpha \end{pmatrix})}

이 경우 순행렬에 대한 위의 관계는 다음을 제공하기 위해 명시적으로 해결될 수 있습니다.

P(t)={\begin{pmatrix}{\frac{\beta}{\alpha +\beta}}+{\frac{\alpha}{\alpha +\beta}}e^{-(\alpha +\beta)t}&,{\frac{\alpha}{\alpha +\beta}}-{\frac{\alpha}{\alpha +\beta}}e^{-(\alpha +\beta)t}\\{\frac{\beta}{\alpha +\beta}}-{\frac{\beta}{\alpha +\beta}}e^{-(\alpha +\beta)t}&,{\frac{\alpha}{\alpha +\beta}}와{\fr.교류{\beta}{\alpha +\alpha }}e^{-(\alpha +\alpha )t}\end{pmatrix}

그러나 직접 해법은 더 큰 행렬에 대해 계산하기가 복잡합니다.Q가 행렬의 반군의 생성자라는 사실

P(t+s)=e^{(t+s)Q}=e^{tQ}e^{sQ}=P(t)P(s)

사용됩니다.

고정 분포

환원 불가능한 반복 CTMC에 대한 정상 분포는 프로세스가 t의 큰 값에 대해 수렴하는 확률 분포입니다. 이전에 고려된 두 상태 프로세스에 대해 다음과 같이 주어진 P(t)에 대해 관찰하십시오.

P(t)={\begin{pmatrix}{\frac{\beta}{\alpha +\beta}}+{\frac{\alpha}{\alpha +\beta}}e^{-(\alpha +\beta)t}&,{\frac{\alpha}{\alpha +\beta}}-{\frac{\alpha}{\alpha +\beta}}e^{-(\alpha +\beta)t}\\{\frac{\beta}{\alpha +\beta}}-{\frac{\beta}{\alpha +\beta}}e^{-(\alpha +\beta)t}&,{\frac{\alpha}{\alpha +\beta}}와{\fr.교류{\beta}{\alpha +\alpha }}e^{-(\alpha +\alpha )t}\end{pmatrix}

t → ∞으로 인해 분포는 다음과 같은 경향이 있습니다.

P_{\pi }=pmatrix{\frac}{\alpha +\flac }{\frac {\alpha +\flac }{\flac }{\flac }{\alpha +\fmatrix}}\frac {\fmatrix

각 행의 분포는 시작 상태에 따라 달라지지 않으므로 유의하십시오.행 벡터 $θ$ 는 다음을 통해 구할^[17] 수 있다.

\displaystyle \pi Q=0.}

라는 추가적인 제약을 가하여

\displaystyle \sum _{i\in S}\pi _{i}=1.}

예 1

금융 시장 상태를 나타내는 연속 시간 마르코프 체인의 유도 그래프 표현(주: 숫자는 구성됨).

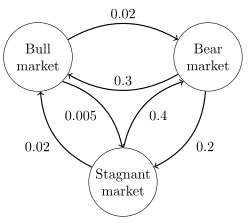
오른쪽 이미지는 상태 공간 {Bull market, Bear market, Stained market} 및 전이율 매트릭스를 가진 연속 시간 마르코프 체인을 나타냅니다.

({displaystyle Q=pmatrix}-0.025&0.02&0.005\0.3&-0.5&0.2\0.02&-0.42&-0.42\end{pmatrix})}

이 체인의 정상 분포는 § $\pi Q=0$ $\pi Q=0$ {\ $displaystyle \pi$ Q $=0$ 을(를) 해결하여 구할 수 있으며, 원소의 합계가 1이어야 합니다.

\displaystyle \pi = pmatrix 0 입니다.885&0.071&0.044\end{pmatrix}.}

예 2

상태 1, 5, 6, 8에 대한 예시로, 전이 확률이 있는 전이 그래프.스테이트 2와 스테이트8 사이에는 쌍방향 비밀 통로가 있습니다.

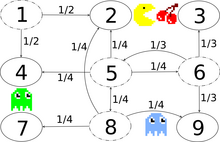
오른쪽 이미지는 상태 공간이 {1,2,3,4,5,6,7,8,9}인 이산 시간 마르코프 연쇄 모델링 팩맨을 나타냅니다.플레이어는 팩맨을 미로를 통해 조종하며 팩팟을 먹는다.한편, 그는 유령에게 쫓기고 있다.편의상 미로는 작은 3x3 그리드로 하고 몬스터는 수평 및 수직 방향으로 무작위로 이동합니다.상태 2와 상태 8 사이의 비밀 통로는 양방향으로 사용할 수 있다.확률이 0인 엔트리는 다음 전이율 매트릭스에서 삭제됩니다.

$Q={\begin{pmatrix}-1&,{\frac{1}{2}}&&{\frac{1}{2}}\\{\frac{1}{4}}&-1&,{\frac{1}{4}}&&{\frac{1}{4}}&&&{\frac{1}{4}}\\&,{\frac{1}{2}}&-1&,&&{\frac{1}{2}}\\{\frac{1}{3}}&&&-1&,{\frac{1}{3}}&&{\frac{1}{3}}\\&,{\frac{1}{4}}&&{\frac{1}{4}.}&-1&,{\frac{1}{4}}&&{\frac{1}{4}}\\&,&{\frac{1}{3}}&&{\frac{1}{3}}&-1&,&&{\frac{1}{3}}\\&,&&,{년.frac {1}{2}}&-1&{\frac {1}{2}}\&{\frac {1}{4}&{\frac {1}{4}&{\frac {1}{4}&1}&{\frac {4}&{\frac {1}{4}&{frac}&{frac$

이 마르코프 사슬은 환원할 수 없다. 왜냐하면 유령은 유한한 시간 안에 모든 상태에서 모든 상태로 날아갈 수 있기 때문이다.비밀 통로로 인해, 마르코프 사슬은 또한 비주기적인데, 이는 몬스터가 짝수 또는 불균일한 수의 상태 천이 모두에서 어떤 상태에서 어떤 상태로든 이동할 수 있기 때문이다.따라서, 고유한 정상 분포가 존재하며, 원소의 합계가 1이어야 하는 제약 조건을 조건으로 $\pi Q=0$ Q $\pi Q=0$ { $displaystyle \pi$ Q= $0$ 을 풀면 찾을 수 있습니다.이 제약조건의 선형방정식의 해는 $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ ( $7$ $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ .7 $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ , $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ 7 $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ , $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ 4 $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ 입니다 $.\$ $displaystyle \pi$ = ( $7.7$ , $15.4, 11.5, 11.7, 11.7,$ 11. $7$ , 15.7, $15$ .7 $)%$ 입니다.} 인접한 $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$ 비밀통로의 중앙상태와 경계상태 2, 8이 가장 많이 들락날락하고 모서리상태의 방문이 가장 적게 들락날락한다 $.$

시간 반전

CTMC_t X의 경우, 시간 지연 ${\hat {X}}_{t}=X_{T-t}$ 는 ${\hat {X}}_{t}=X_{T-t}$ ^ ${\hat {X}}_{t}=X_{T-t}$ ${\hat {X}}_{t}=X_{T-t}$ ${\hat {X}}_{t}=X_{T-t}$ T ${\hat {X}}_{t}=X_{T-t}$ - ${\hat {X}}_{t}=X_{T-t}$ \ $displaystyle$ \ hat ${ X} _$ { t } $=$ X ${\hat {X}}_{t}=X_{T-t}$ _ { T - ${\hat {X}}_{t}=X_{T-t}$ t ${\hat {X}}_{t}=X_{T-t}$ } 로 정의됩니다.이 프로세스는 순방향 프로세스와 동일한 고정 분포를 가집니다.

체인(chain)은 반전 프로세스가 순방향 프로세스와 동일할 경우 가역적이라고 합니다.Kolmogorov의 기준은 프로세스를 되돌릴 수 있는 필요충분조건은 닫힌 루프 주위의 전이율의 곱이 양방향에서 동일해야 한다는 것이다.

임베디드 마르코프 연쇄

에르고딕 연속시간 마르코프 사슬 Q의 정상확률 분포 $θ$ 를 구하는 방법 중 하나는 우선 내장된 마르코프 사슬(EMC)을 찾는 것이다.엄밀히 말하면 EMC는 정규 이산 시간 마르코프 체인입니다.EMC, S의 1단계 전이 확률 행렬의 각 요소는 s로_ij 나타내며, 상태 i에서 상태 j로 이행할 조건부 확률을 나타낸다.이러한 조건부 확률은 다음과 같이 구할 수 있습니다.

s_{ij}=cases{\frac {q_{ij}}{\sum _ {k\neq i}q_{ik}}&{\text {neq j\0&{text}}}}.\end {case}

이로부터 S는 다음과 같이 쓸 수 있다.

S=I-\left(\operatorname {diag}(Q)\오른쪽)^{-1}Q

여기서 I는 항등행렬이고 diag(Q)는 행렬 Q에서 주 대각선을 선택하고 다른 모든 요소를 0으로 설정하여 형성된 대각행렬입니다.

정상 확률 분포 벡터를 찾으려면 다음 $§(\displaystyle \varphi)$ 를 $\varphi$ 찾아야 합니다.

\displaystyle \varphi S=\varphi ,}

${\$ { $displaystyle \$ $varphi$ $}$ $\|\varphi \|_{1}$ $\varphi$ $\varphi$ $,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,$ \ $displaystyle \ varphi$ \ $_ {1}$ = $\|\varphi \|_{1}$ 1. 여기서 $may$ 는 다음과 같이 표시됩니다.

\pi = {-\varphi (\operatorname {diag} (Q)} \over \left \ varphi (\operatorname {diag} (Q) {{-1} \right \ {1}}

(S는 Q가 정기적이지 않은 경우에도 주기적일 수 있습니다. $is$ 이 발견되면 단위 벡터로 정규화해야 합니다.)

연속 시간 마르코프 사슬에서 파생될 수 있는 또 다른 이산 시간 과정은 δ 단위 시간 간격으로 X(t)를 관찰하여 형성된 (이산 시간) 마르코프 사슬인 γ-스켈튼이다.랜덤 변수 X(0), X(θ), X(2'), ...는 γ-skeleton이 방문한 상태의 시퀀스를 나타냅니다.

「」를 참조해 주세요.

콜모고로프 방정식(마르코프 점프 과정)

메모들

^ Ross, S.M. (2010). Introduction to Probability Models (10 ed.). Elsevier. ISBN 978-0-12-375686-2.
^ 앤더슨 1991, 64페이지의 정의를 참조하십시오.
^ Chen & Mao 2021, 정의 2.2.
^ Chen 2004, 정의 0.1(4)
^ 노리스 1997, 정리 2.8.4 및 정리 2.8.2(b)
^ ^a ^b 앤더슨 1991, 정리 2.2.2(1), 70페이지.
^ 앤더슨 1991, 정의(81페이지)
^ 2004년 첸, 2페이지.
^ 앤더슨 1991, 20페이지.
^ ^a ^b Suhov & Kelbert 2008, 정의 2.6.3.
^ Chen & Mao 2021, 정의 2.1.
^ Chen 2004, 정의 0.1.
^ Chen & Mao 2021 (56페이지), 정의 2.2 바로 아래.
^ 노리스 1997, 87페이지
^ 수호브 & 켈버트 2008, 정리 2.6.6.
^ 노리스 1997, 정리 2.8.2(c)
^ Norris, J. R. (1997). "Continuous-time Markov chains II". Markov Chains. pp. 108–127. doi:10.1017/CBO9780511810633.005. ISBN 9780511810633.

레퍼런스

Anderson, William J. (1991). Continuous-time Markov chains: an applications-oriented approach. Springer.
Leo Breiman(1992) [1968] 확률.애디슨 웨슬리 원판, 산업 응용 수학 학회 ISBN 0-89871-296-3 전재 (7장 참조)
Chen, Mu-Fa (2004). From Markov chains to non-equilibrium particle systems (Second ed.). World Scientific.
Chen, Mu-Fa; Mao, Yong-Hua (2021). Introduction to stochastic processes. World Scientific.
J. L. Doob(1953) 확률적 과정.뉴욕: John Wiley and Sons ISBN 0-471-52369-0.
A. A. 마르코프(1971년)."확률 이론의 한계 이론의 연계를 연쇄적으로 연결된 변수의 합으로 확장." 부록 B에 전재되었다.하워드.동적 확률론적 시스템, 제1권: 마르코프 연쇄.존 와일리와 아들들.
Markov, A. A. (2006). Translated by Link, David. "An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains". Science in Context. 19 (4): 591–600. doi:10.1017/s0269889706001074.
S. P. 마인과 R. L. 트위디(1993) 마르코프 사슬과 확률적 안정성.런던: Springer-Verlag ISBN 0-387-19832-6.온라인:MCSS.두 번째 판, 캠브리지 대학 출판부, 2009.
Kemeny, John G.; Hazleton Mirkil; J. Laurie Snell; Gerald L. Thompson (1959). Finite Mathematical Structures (1st ed.). Englewood Cliffs, NJ: Prentice-Hall, Inc. Library of Congress Card Catalog Number 59-12841. 고전 텍스트. cf 6장 유한 마르코프 연쇄 페이지 384ff.
John G. Kemeny & J. Laurie Snell (1960) Finite Markov Chains, D. van Nostrand Company ISBN 0-442-04328-7
E. Nummelin. "General irreducible Markov chains and non-negative operators". Cambridge University Press, 1984, 2004. ISBN 0-521-60494-X
Seneta, E. Non-negative matrices and Markov chains. 2nd rev. ed., 1981, XVI, 288 p., Softcover Springer Series in Statistics. (Originally published by Allen & Unwin Ltd., London, 1973) ISBN 978-0-387-29765-1
Suhov, Yuri; Kelbert, Mark (2008). Markov chains: a primer in random processes and their applications. Cambridge University Press.

^ For instance, consider the example $S=\mathbb {Z} _{\geq 0}$ and $Q$ being the (unique) transition rate matrix on $S$ such that $\forall i\in \mathbb {Z} _{\geq 0}~~Q_{i,i+1}=i^{2},~Q_{i,i}=-i^{2}$ . (Then the remaining entries of $Q$ will all be zero. Cf. birth process.) Then $Q$ is irregular. Then, for general infinite $S$ , indexing $S$ by the nonnegative integers $\mathbb {Z} _{\geq 0}$ yields that a suitably modified version of the above matrix $Q$ will be irregular.^[9]

[ross-1] Ross, S.M. (2010). Introduction to Probability Models (10 ed.). Elsevier. ISBN 978-0-12-375686-2.

[FOOTNOTEAnderson1991See_definition_on_page_64-2] 앤더슨 1991, 64페이지의 정의를 참조하십시오.

[FOOTNOTEChenMao2021Definition_2.2-3] Chen & Mao 2021, 정의 2.2.

[FOOTNOTEChen2004Definition_0.1(4)-4] Chen 2004, 정의 0.1(4)

[FOOTNOTENorris1997Theorem_2.8.4_and_Theorem_2.8.2(b)-5] 노리스 1997, 정리 2.8.4 및 정리 2.8.2(b)

[FOOTNOTEAnderson1991Theorem_2.2.2(1),_page_70-6] 앤더슨 1991, 정리 2.2.2(1), 70페이지.

[FOOTNOTEAnderson1991Definition_on_page_81-7] 앤더슨 1991, 정의(81페이지)

[FOOTNOTEChen2004page_2-8] 2004년 첸, 2페이지.

[FOOTNOTEAnderson1991page_20-9] 앤더슨 1991, 20페이지.

[FOOTNOTESuhovKelbert2008Definition_2.6.3-11] Suhov & Kelbert 2008, 정의 2.6.3.

[FOOTNOTEChenMao2021Definition_2.1-12] Chen & Mao 2021, 정의 2.1.

[FOOTNOTEChen2004Definition_0.1-13] Chen 2004, 정의 0.1.

[FOOTNOTEChenMao2021page_56,_just_below_Definition_2.2-14] Chen & Mao 2021 (56페이지), 정의 2.2 바로 아래.

[FOOTNOTENorris1997page_87-15] 노리스 1997, 87페이지

[FOOTNOTESuhovKelbert2008Theorem_2.6.6-16] 수호브 & 켈버트 2008, 정리 2.6.6.

[FOOTNOTENorris1997Theorem_2.8.2(c)-17] 노리스 1997, 정리 2.8.2(c)

[norris2-18] Norris, J. R. (1997). "Continuous-time Markov chains II". Markov Chains. pp. 108–127. doi:10.1017/CBO9780511810633.005. ISBN 9780511810633.

[10] For instance, consider the example $S=\mathbb {Z} _{\geq 0}$ and $Q$ being the (unique) transition rate matrix on $S$ such that $\forall i\in \mathbb {Z} _{\geq 0}~~Q_{i,i+1}=i^{2},~Q_{i,i}=-i^{2}$ . (Then the remaining entries of $Q$ will all be zero. Cf. birth process.) Then $Q$ is irregular. Then, for general infinite $S$ , indexing $S$ by the nonnegative integers $\mathbb {Z} _{\geq 0}$ yields that a suitably modified version of the above matrix $Q$ will be irregular.^[9]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[10]

[11]

[12]

[15]

[16]

[17]

[9]

v t Queueing theory
Single queueing nodes	D/M/1 queue M/D/1 queue M/D/c queue M/M/1 queue Burke's theorem M/M/c queue M/M/∞ queue M/G/1 queue Pollaczek–Khinchine formula Matrix analytic method M/G/k queue G/M/1 queue G/G/1 queue Kingman's formula Lindley equation Fork–join queue Bulk queue
Arrival processes	Poisson point process Markovian arrival process Rational arrival process
Queueing networks	Jackson network Traffic equations Gordon–Newell theorem Mean value analysis Buzen's algorithm Kelly network G-network BCMP network
Service policies	FIFO LIFO Processor sharing Round-robin Shortest job next Shortest remaining time
Key concepts	Continuous-time Markov chain Kendall's notation Little's law Product-form solution Balance equation Quasireversibility Flow-equivalent server method Arrival theorem Decomposition method Beneš method
Limit theorems	Fluid limit Mean-field theory Heavy traffic approximation Reflected Brownian motion
Extensions	Fluid queue Layered queueing network Polling system Adversarial queueing network Loss network Retrial queue
Information systems	Data buffer Erlang (unit) Erlang distribution Flow control (data) Message queue Network congestion Network scheduler Pipeline (software) Quality of service Scheduling (computing) Teletraffic engineering
Category

Search

연속 시간 마르코프 연쇄

네임스페이스

더

목차

정의.

전이 확률 정의

점프 체인/홀딩 타임 정의

오른쪽 연속 함수와 연관된 시퀀스

점프 매트릭스 δ의 정의

점프 체인/홀드 타임 속성

극소 정의

특성.

커뮤니케이션 클래스

일시적인 동작

고정 분포

예 1

예 2

시간 반전

임베디드 마르코프 연쇄

「」를 참조해 주세요.

메모들

레퍼런스

Search

연속 시간 마르코프 연쇄

정의.

전이 확률 정의

점프 체인/홀딩 타임 정의

오른쪽 연속 함수와 연관된 시퀀스

점프 매트릭스 δ의 정의

점프 체인/홀드 타임 속성

극소 정의

특성.

커뮤니케이션 클래스

일시적인 동작

고정 분포

예 1

예 2

시간 반전

임베디드 마르코프 연쇄

「 」를 참조해 주세요.

메모들

레퍼런스

「」를 참조해 주세요.