안티프리즘

균일 n각 반각형 집합
균일 n각 반각형 집합
	균일 육각형 안티프리즘 (n = 6)
유형	반정형 다면체라는 의미에서 균일한.
얼굴들	정n각형 2개; 2n정삼각형
가장자리	4n
꼭짓점	2n
꼭짓점 구성	3.3.3.n
슐레플리 기호	{ } ⊗{n} ; s{2,2n}; sr{2,n}
콘웨이 표기법	안
콕서터 다이어그램	;
대칭군	Dnd, [2+,2n], (2*n), order 4n
회전군	Dn, [2,n]+, (22n), order 2n
이중 다면체	볼록 이중 균일 n각 사다리꼴
특성.	볼록, 정점-일시적, 정다각형 면, 합동 & 동축 기저
그물
	균일한 정각 반각의 그물(n = 9)

기하학에서, n-각 반각(n-角, ) 또는 n-반각(n-antiprism)은 $2n개$ 의 삼각형의 교대 띠로 연결된, n-변 다각형의 두 개의 평행한 직접 복사로 구성된 다면체입니다. 이들은 콘웨이 $표기법$ An으로 표현됩니다.

안티프리즘은 프리즘의 하위 분류이며, 스너브 다면체의 (퇴화된) 유형입니다.

안티프리즘은 염기가 서로 상대적으로 꼬여 있고, 측면(염기를 연결하는)이 $n개$ 의 4사변이 아닌 $2n개$ 의 삼각형이라는 점을 제외하고는 프리즘과 유사합니다.

n각 반원뿔의 이중 다면체는 n각 사다리꼴입니다.

역사

요하네스 케플러는 그의 1619년 저서 '하모니세스 문디'에서 무한한 반프리즘 계열의 존재를 관찰했습니다.^[2] 이것은 전통적으로 이 모양들의 최초의 발견으로 여겨져 왔지만, 그것들은 더 일찍 알려져 있었을지도 모릅니다: 육각형의 안티프리즘 그물을 위한 서명되지 않은 인쇄 블록은 1556년에 사망한 Hieronymus Andreae에게 귀속되었습니다.^[3]

독일어의 "반프리즘"이라는 단어는 19세기에 사용되었고, 칼 하인제는 테오도르 비트슈타인에게 그 도입을 공으로 돌렸습니다.^[4] 영어의 "반프리즘"은 1차 최적 원소의 효과를 제거하기 위해 사용된 광학 프리즘에 대해 이전에 사용되었지만,^[5] 기하학적 의미에서 영어에서 "반프리즘"이 처음 사용된 것은 20세기 초 H. S. M. 콕서터의 작품에서 나타난 것으로 보입니다.^[6]

특수한 경우

오른쪽 반프리즘

일반적으로 n-곤 기저를 갖는 반각형의 경우, 일반적으로 이 두 $사본$ 이180/ $n$ 도 각도만큼 꼬여 있는 경우를 고려합니다.

일반 다각형의 축은 다각형 평면에 수직이고 다각형 중심에 있는 선입니다.

합동인 $정규$ n-곤 기저가 $180$ /n도 각도만큼 꼬여 있는 반프리즘의 경우, 기저가 같은 축을 가지면 더 많은 규칙성이 얻어집니다. 즉, (비평면 기저의 경우) 기저 중심을 연결하는 선이 기저 평면과 수직인 경우. 그러면 반각을 오른쪽 반각이라고 하고, 그 $2개$ 의 면은 이등변삼각형입니다.

균일반프리즘

균일한 n-항원은 두 개의 합동 정칙 n-곤을 밑면으로 하고, $두$ 개의 정삼각형을 변면으로 합니다.

균일한 반 프리즘은 균일한 프리즘과 마찬가지로 무한한 종류의 정점-경향 다면체를 형성합니다. $n$ = $2$ 인 경우, 정사면체는 디곤 안티프리즘(퇴행 안티프리즘)이고, n = 3인 경우 정사면체는 삼각 안티프리즘(퇴행 안티프리즘)입니다.

등각항원류
v
t
안티프리즘명	디곤 안티프리즘	(삼각형) 삼각 반프리즘	(4각형) 제곱 반프리즘	오각반경	육각형 반프리즘	칠각반프리즘	...	유인원적 반프리즘
다면체 영상							...
구면 타일 이미지							평면 타일 이미지
꼭짓점 구성.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

이러한 반정규항원의 슐레겔 도표는 다음과 같습니다.

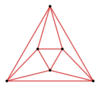A3	A4	A5	A6	A7	A8

직각좌표

오른쪽 n-반원뿔의 꼭짓점에 대한 직각좌표(즉, 정n-곤 기저와 $2개$ 의 이등변 삼각형 변을 갖는 것)는 다음과 같습니다.

\left(\cos {\frac {k\pi}{n}},\sin {\frac {k\pi}{n}}, (-1)^{k}h\right)

where $0 \leq k \leq 2 n - 1$ ;

n-antip리즘이 균일하면(즉, 삼각형이 정삼각형인 경우), 다음과 같습니다.

2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.

부피 및 표면적

a를 균일한 n각 안티프리즘의 가장자리 길이라 하고 부피는 다음과 같습니다.

V=~n{\frac {{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}~a^{3},

표면적은 다음과 같습니다.

A={\frac {n}{2}}\left(\cot {\frac {\pi}{n}}+{\sqrt {3}}\right)a^{2}

또한 $기저$ 의 한 변의 길이와 높이 $h$ 를 갖는 직각 반각형의 부피는 다음과 같습니다.

V={\frac {nhl^{2}}{12}}\left(\csc {\frac {\pi}{n}}+2\cot {\frac {\pi}{n}}\right)

$동일$ 한 $l$ 과 h를 갖는 오른쪽 n각 프리즘의 부피는 다음과 같습니다.

V_{\mathrm {prism}} ={\frac {nhl^{2}}{4}}\cot {\frac {\pi}{n}

안티프리즘보다 작은 크기입니다.

대칭성

오른쪽 n antip리즘의 대칭군(즉, 정직렬 기저와 이등변 면을 갖는)은 다음의 경우를 제외하고는 $4n$ 의 D = D입니다.

$n$ $=$ $2$ : D의 세 가지 버전을 부분군으로 갖는 24 $=$ 3 × (4 × 2)의 더 큰 대칭군 T를 갖는 정사면체 $;$

$n$ $=$ $3$ : 정팔면체 $,$ 48 $=$ 4 × (4 × 3) 순서의 대칭군 O가 더 큰 정팔면체, D의 네 가지 버전을 부분군으로 포함합니다.

$대칭$ 그룹은 n이 홀수인 경우에만 반전을 포함합니다.

회전 그룹은 다음의 경우를 제외하고 $2n차$ 의 $D$ 입니다_n.

$n$ $=$ $2$ : 3 × (2 × 2) 차수 12 $=$ 3 × (2 × 2)의 회전군 T가 더 큰정사면체를 부분군으로 3가지 버전의 D를 갖는 정사면체;

$n$ $=$ $3$ : 정팔면체 $,$ 24 $=$ 4 × (2 × 3)의 회전군 O가 더 큰 정팔면체, 4가지 버전의 D를 부분군으로 포함합니다.

참고: $오른쪽$ n-항원은 합동 정칙 n-곤 기저와 합동 이등변 삼각형 변을 가지므로 $n$ ≥ 4에 대하여 균일한 n-항원과 같은 (이중체) 대칭군을 갖습니다.

일반화

더 높은 차원에서

4차원 안티프리즘은 두 개의 이중 다면체를 평행한 대향 면으로 가지는 것으로 정의할 수 있으므로, 그들 사이의 각 3차원 면은 다면체의 두 개의 이중 부분, 즉 정점과 이중 다각형, 또는 두 개의 이중 모서리로부터 나옵니다. 모든 3차원 볼록 다면체는 표준 다면체와 극이중성체로 구성된 4차원 반프리즘의 두 개의 반대 면 중 하나와 조합적으로 동등합니다.^[7] 그러나 이들의 쌍체와 결합하여 5차원 안티프리즘을 형성할 수 없는 4차원 다면체가 존재합니다.^[8]

자기 교차 다면체

5/2-antiprism		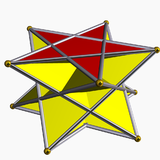	5/3-antiprism
9/2-antiprism		9/4-antiprism		9/5-antiprism

이것은 29각형의 면과 함께 15면까지의 비별과 별의 반각형을 모두 보여줍니다.

균일한 별 반 프리즘은 별 다각형 염기 { $p / q}$ 에 의해 이름이 지어지며, 프로그레이드와 역행(교차) 솔루션에 존재합니다. 교차된 형태는 교차하는 꼭짓점 도형을 가지며, $p / q$ 대신 p $/(p$ – $q),$ 예: 5/2 대신 5/3으로 표시됩니다.

오른쪽 별 반각형은 합동 동축 정볼록 또는 별 다각형 기저면 두 개와 이등변 삼각형 측면 $두$ 개를 가지고 있습니다.

규칙적인 볼록하거나 다각형 염기를 가진 모든 별 반각형은 (필요한 경우, 염기들 중 하나를 번역하거나 비틀어) 오른쪽 별 반각형을 만들 수 있습니다.

역행 형태에서는 아니지만 진행 형태에서는 볼록하거나 별 베이스를 잇는 삼각형이 회전 대칭의 축과 교차합니다. 따라서:

규칙적인 볼록 다각형 기저를 갖는 역행성 반각형은 모든 모서리 길이가 같을 수 없으므로 균일할 수 없습니다. "예외": 정삼각형 밑면(정삼각형 구성: 3.3/2.3.3)을 가진 역행성 반각형은 균일할 수 있지만, 정삼각형의 모습을 하고 있습니다: 퇴화된 별 다면체입니다.

마찬가지로, 일반적인 항성 다각형 염기를 가진 일부 역행 항성 반각형은 모든 동일한 모서리 길이를 가질 수 없으므로 균일할 수 없습니다. 예: 일반적인 항성 7/5-곤 염기(정점 구성: 3.3.3.7/5)를 가진 역행성 반원성은 균일할 수 없습니다.

$또한$ p와 $q$ 가 공통적인 인자를 갖는 경우, 규칙적인 $항성$ p/q-gon 염기를 갖는 항성 안티프리즘 화합물을 구성할 수 있습니다. 예: 별 10/4-항원은 두 개의 별 5/2-항원의 화합물입니다.

대칭

에 의한

스타

p/q-항원

, p ≤

12

대칭군	균일한 별			오른쪽 별
$라 4d [2 +,8] (2*4)$				3.3/2.3.4 교차 제곱 반프리즘
$라 5h [2,5] (*225)$	3.3.3.5/2 오순대항해			3.3/2.3.5 엇갈린 오각형의 반제국주의
$라 5d [2 +,10] (2*5)$	3.3.3.5/3 오순교 교차항원
$라 6d [2 +,12] (2*6)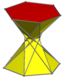$				3.3/2.3.6 엇갈린 육각형의 반제국주의
$라 7h [2,7] (*227)$	3.3.3.7/2	3.3.3.7/4
$라 7d [2 +,14] (2*7)$	3.3.3.7/3
$라 8d [2 +,16] (2*8)$	3.3.3.8/3 옥타그램 안티프리즘	3.3.3.8/5 옥타그램 교차항원론
$라 9h [2,9] (*229)$	3.3.3.9/2 근위축성 항진증(9/2)	3.3.3.9/4 근위축성 항진증(9/4)
$라 9d [2 +,18] (2*9)$	3.3.3.9/5 에니어그램 교차항원론
$라 10d [2 +,20] (2*10)$	3.3.3.10/3 디카그램 안티프리즘
$라 11h [2,11] (*2.2.11)$	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
$라 11d [2 +,22] (2*11)$	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
$라 12d [2 +,24] (2*12)$	3.3.3.12/5	3.3.3.12/7
...	...

참고 항목

4차원 폴리토프인 그랜드 안티프리즘
볼록 껍질이 반프리즘인 3차원 다각형인 스큐 다각형

참고문헌

^ N.W. 존슨: 기하학과 변신, (2018) ISBN978-1-107-10340-5장: 유한대칭군, 11.3 피라미드, 프리즘, 안티프리즘, 그림 11.3c
^ Kepler, Johannes (1619). "Book II, Definition X". Harmonices Mundi (in Latin). p. 49. 또한 7각 반각의 그림 A를 참조하십시오.
^ Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (July 2008). "New light on the rediscovery of the Archimedean solids during the Renaissance". Archive for History of Exact Sciences. 62 (4): 457–467. JSTOR 41134285.
^ Heinze, Karl (1886). Lucke, Franz (ed.). Genetische Stereometrie (in German). B. G. Teubner. p. 14.
^ Smyth, Piazzi (1881). "XVII. On the Constitution of the Lines forming the Low-Temperature Spectrum of Oxygen". Transactions of the Royal Society of Edinburgh. 30 (1): 419–425. doi:10.1017/s0080456800029112.
^ Coxeter, H. S. M. (January 1928). "The pure Archimedean polytopes in six and seven dimensions". Mathematical Proceedings of the Cambridge Philosophical Society. 24 (1): 1–9. doi:10.1017/s0305004100011786.
^ Grünbaum, Branko (2005). "Are prisms and antiprisms really boring? (Part 3)" (PDF). Geombinatorics. 15 (2): 69–78. MR 2298896.
^ Dobbins, Michael Gene (2017). "Antiprismlessness, or: reducing combinatorial equivalence to projective equivalence in realizability problems for polytopes". Discrete & Computational Geometry. 57 (4): 966–984. doi:10.1007/s00454-017-9874-y. MR 3639611.

외부 링크

위키미디어 커먼즈의 안티프리즘 관련 미디어
Weisstein, Eric W. "Antiprism". MathWorld.
논볼렉스 프리즘과 안티프리즘
프리즘과 안티프리즘의 종이 모형

[1] N.W. 존슨: 기하학과 변신, (2018) ISBN978-1-107-10340-5장: 유한대칭군, 11.3 피라미드, 프리즘, 안티프리즘, 그림 11.3c

[2] Kepler, Johannes (1619). "Book II, Definition X". Harmonices Mundi (in Latin). p. 49. 또한 7각 반각의 그림 A를 참조하십시오.

[3] Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (July 2008). "New light on the rediscovery of the Archimedean solids during the Renaissance". Archive for History of Exact Sciences. 62 (4): 457–467. JSTOR 41134285.

[4] Heinze, Karl (1886). Lucke, Franz (ed.). Genetische Stereometrie (in German). B. G. Teubner. p. 14.

[5] Smyth, Piazzi (1881). "XVII. On the Constitution of the Lines forming the Low-Temperature Spectrum of Oxygen". Transactions of the Royal Society of Edinburgh. 30 (1): 419–425. doi:10.1017/s0080456800029112.

[6] Coxeter, H. S. M. (January 1928). "The pure Archimedean polytopes in six and seven dimensions". Mathematical Proceedings of the Cambridge Philosophical Society. 24 (1): 1–9. doi:10.1017/s0305004100011786.

[7] Grünbaum, Branko (2005). "Are prisms and antiprisms really boring? (Part 3)" (PDF). Geombinatorics. 15 (2): 69–78. MR 2298896.

[8] Dobbins, Michael Gene (2017). "Antiprismlessness, or: reducing combinatorial equivalence to projective equivalence in realizability problems for polytopes". Discrete & Computational Geometry. 57 (4): 966–984. doi:10.1007/s00454-017-9874-y. MR 3639611.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search