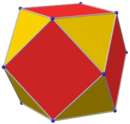
아르키메데스의 입체

Archimedean solid
잘린 사면체, 정육면체 및 잘린 정이십이면체.첫 번째와 마지막은 각각 가장 작은 아르키메데스 고체와 가장 큰 아르키메데스 고체로 묘사될 수 있다.
마름모 정육면체와 의사 정육면체

기하학에서, 아르키메데스의 다면체는 아르키메데스가 처음 열거한 13개의 다면체 중 하나이다.그것들은 5개의 플라톤 고체(폴리곤의 한 종류로만 구성됨)를 제외하고 프리즘과 반프리즘을 제외하며 의사옴비큐브팔면체를 제외한 [1]동일한 꼭지점에서 만나는 정다각형으로 구성된 볼록한 균일한 다면체이다.이들은 정다각형 면이 동일한 정점에서 만날 필요가 없는 Johnson 솔리드의 부분 집합입니다.

"동일 꼭지점"은 두 개의 꼭지점이 서로 대칭임을 의미합니다. 전체 고체의 전역 등각계는 고체를 초기 위치에 직접 놓으면서 한 꼭지점을 다른 꼭지점으로 옮깁니다.Branko Grünbaum(2009)은 14번째 다면체인 길쭉한 정사각형 자이로비쿠폴라(또는 의사-롬비큐브팔면체)가 아르키메데스 고체의 더 약한 정의를 충족한다고 관찰했다. 여기서 "동일 정점"은 각 정점을 둘러싼 면들이 단지 같은 유형임을 의미한다(즉, 각 정점은 가까이서만 동일하다).ry는 필수입니다.Grünbaum은 작가들이 아르키메데스의 다면체를 이 국소적 정의를 사용하여 정의하지만 14번째 다면체는 생략하는 빈번한 오류를 지적했다.13개의 다면체만 나열되는 경우 정의는 국소 근방이 아닌 다면체의 전역 대칭을 사용해야 합니다.

대칭군이 이면체군인 프리즘과 반프리즘은 그들의 면이 정다각형이고 그들의 대칭군이 정점에 횡방향으로 작용하더라도 일반적으로 아르키메데스의 고체로 간주되지 않는다.이 두 무한족들을 제외하면, 아르키메데스의 다면체는 13개이다.모든 아르키메데스 고형물(장방형 자이로비쿠폴라 제외)은 사면체, 팔면체 및 이십면체 대칭을 가진 플라톤 고형물로부터 위트호프 구조를 통해 만들어질 수 있다.

이름 유래

아르키메데스의 고형물은 지금은 사라진 작품에서 그것들을 논의한 아르키메데스로부터 이름을 따왔다.파푸스는 그것을 언급하며 아르키메데스가 13개의 [2]다면체를 나열했다고 말했다.르네상스 기간 동안에, 예술가, 수학자들. 자세한 정보는(참조하십시오 슈라이버, 피셔 &, Sternath 2008년에 높은 대칭과 약 1620년에 요하네스 케플러는 13polyhedra,[3]의 재발견뿐만 아니라 프리즘 antiprisms, 그리고 비볼록형 고체 Kepler-Poinsot 다면체로 알려진 정의를 완성했다고 순수한 형태 이른다.를 빌리려e 르네상스 시대의 아르키메데스 고체의 재발견)

케플러는 또한 길쭉한 정사각형 자이로비쿠폴라를 발견했을지도 모른다: 적어도 한때 그는 14개의 아르키메데스 고체가 있었다고 진술했다.그러나 그가 출판한 목록에는 13개의 균일한 다면체만 포함되어 있으며, 의사옴비큐브팔면체의 존재에 대한 최초의 명확한 진술은 1905년 던컨 소머빌에 [2]의해 이루어졌다.

분류

13개의 아르키메데스 고체가 있다(길쭉한 정사각형 자이로비쿠폴라를 세지 않는다; 두 개의 반동형체, 즉 스너브 큐브와 스너브 12면체의 거울 이미지가 별도로 세지면 15).

여기서 정점 구성은 주어진 정점에서 만나는 규칙적인 다각형 유형을 나타냅니다.예를 들어, 정점 구성이 4.6.8이면 정사각형, 육각형 및 팔각형은 정점에서 만난다는 것을 의미합니다(정점 주위에서 시계 방향으로 순서가 지정됨).

이름/
(대체 이름)		 슐레플리
콕서터 		투과적 단단한 그물 꼭지점
컨피규레이션/그림 		얼굴 가장자리 현기증 용량
(유닛 가장자리)		 포인트
그룹. 		구면성
잘린 사면체 t{3,3}
CDel node 1.pngCDel 3.pngCDel node 1.pngCDel 3.pngCDel node.png 		Truncated tetrahedron Cog-scripted-svg-blue.svg Polyhedron truncated 4a max.png Polyhedron truncated 4a net.svg 3.6.6
Polyhedron truncated 4a vertfig.png 		8 4개의 삼각형
4 육각형 		18 12 2.710576 Td. 0.7754132
육팔면체
(롬비테트라면체, 삼각 자이로비쿠폴라)		 r{4,3} 또는 rr{3,3}
CDel node.pngCDel 4.pngCDel node 1.pngCDel 3.pngCDel node.png 또는 		Cuboctahedron Cog-scripted-svg-blue.svg Polyhedron 6-8 max.png Polyhedron 6-8 net.svg 3.4.3.4
Polyhedron 6-8 vertfig.png 		14 8개의 삼각형
여섯 칸 		24 12 2.357023 오h 0.9049972
잘린 정육면체 t{4,3}
CDel node 1.pngCDel 4.pngCDel node 1.pngCDel 3.pngCDel node.png 		Truncated hexahedron Cog-scripted-svg-blue.svg Polyhedron truncated 6 max.png Polyhedron truncated 6 net.svg 3.8.8
Polyhedron truncated 6 vertfig.png 		14 8개의 삼각형
6 옥타곤 		36 24 13.599663 오h 0.8494937
잘린 팔면체
(표준 사면체)		 t{3,4} 또는 tr{3,3}
CDel node 1.pngCDel 3.pngCDel node 1.pngCDel 4.pngCDel node.png 또는 		Truncated octahedron Cog-scripted-svg-blue.svg Polyhedron truncated 8 max.png Polyhedron truncated 8 net.svg 4.6.6
Polyhedron truncated 8 vertfig.png 		14 여섯 칸
8 육각형		 36 24 11.313709 오h 0.9099178
마름모 육팔면체
(작은 마름모 육면체, 가늘고 긴 정사각형 오소성 우폴라)		 rr{4,3}
CDel node 1.pngCDel 4.pngCDel node.pngCDel 3.pngCDel node 1.png 		Rhombicuboctahedron Cog-scripted-svg-blue.svg Polyhedron small rhombi 6-8 max.png Polyhedron small rhombi 6-8 net.svg 3.4.4.4
Polyhedron small rhombi 6-8 vertfig.png 		26 8개의 삼각형
18 평방		 48 24 8.714045 오h 0.9540796
깎은 정육면체
(대마름모 육면체)		 tr{4,3}
CDel node 1.pngCDel 4.pngCDel node 1.pngCDel 3.pngCDel node 1.png 		Truncated cuboctahedron Cog-scripted-svg-blue.svg Polyhedron great rhombi 6-8 max.png Polyhedron great rhombi 6-8 net.svg 4.6.8
Polyhedron great rhombi 6-8 vertfig light.png 		26 12개의 정사각형 12칸
8 육각형
6 옥타곤		 72 48 41.798990 오h 0.9431657
스너브 큐브
(스너브 육팔면체)		 sr{4,3}
CDel node h.pngCDel 4.pngCDel node h.pngCDel 3.pngCDel node h.png 		Snub hexahedron (Ccw) Cog-scripted-svg-blue.svg Polyhedron snub 6-8 left max.png Polyhedron snub 6-8 left net.svg 3.3.3.3.4
Polyhedron snub 6-8 left vertfig.png 		38 32개의 삼각형
여섯 칸		 60 24 7.889295 O 0.9651814
이십이면체
(오각형 자이로봇툰다)		 r{5,3}
CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png 		Icosidodecahedron Cog-scripted-svg-blue.svg Polyhedron 12-20 max.png Polyhedron 12-20 net.svg 3.5.3.5
Polyhedron 12-20 vertfig.png 		32 20개의 삼각형
12 펜타곤 		60 30 13.835526 나h 0.9510243
잘린 12면체 t{5,3}
CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png 		Truncated dodecahedron Cog-scripted-svg-blue.svg Polyhedron truncated 12 max.png Polyhedron truncated 12 net.svg 3.10.10
Polyhedron truncated 12 vertfig.png 		32 20개의 삼각형
12 데카곤 		90 60 85.039665 나h 0.9260125
깎은 20면체 t{3,5}
CDel node 1.pngCDel 3.pngCDel node 1.pngCDel 5.pngCDel node.png 		Truncated icosahedron Cog-scripted-svg-blue.svg Polyhedron truncated 20 max.png Polyhedron truncated 20 net compact.svg 5.6.6
Polyhedron truncated 20 vertfig.png 		32 12 펜타곤
20 육각형		 90 60 55.287731 나h 0.9666219
마름모꼴 십이면체
(작은 마름모꼴 12면체)		 rr{5,3}
CDel node 1.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node 1.png 		Rhombicosidodecahedron Cog-scripted-svg-blue.svg Polyhedron small rhombi 12-20 max.png Polyhedron small rhombi 12-20 net.svg 3.4.5.4
Polyhedron small rhombi 12-20 vertfig.png 		62 20개의 삼각형
30 평방
12 펜타곤		 120 60 41.615324 나h 0.9792370
깎은 이십이면체
(큰 마름모꼴 십이면체)		 tr{5,3}
CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.png 		Truncated icosidodecahedron Cog-scripted-svg-blue.svg Polyhedron great rhombi 12-20 max.png Polyhedron great rhombi 12-20 net.svg 4.6.10
Polyhedron great rhombi 12-20 vertfig light.png 		62 30 평방
20 육각형
12 데카곤		 180 120 206.803399 나h 0.9703127
스누브 12면체
(스너브 이십이면체)		 sr {5,3}
CDel node h.pngCDel 5.pngCDel node h.pngCDel 3.pngCDel node h.png 		Snub dodecahedron (Cw) Cog-scripted-svg-blue.svg Polyhedron snub 12-20 left max.png Polyhedron snub 12-20 left net.svg 3.3.3.3.5
Polyhedron snub 12-20 left vertfig.png 		92 80개의 삼각형
12 펜타곤		 150 60 37.616650 I 0.9820114

반정규 다면체의 정의에는 하나 더 있는 그림, 즉 가늘고 긴 정사각형 자이로비쿠폴라 또는 "의사-롬비큐브팔면체"[4]가 포함된다.

특성.

정점의 수는 720°를 정점 각도 결점으로 나눈 값입니다.

정육면체와 정이십이면체는 모서리가 균일하고 준정규체라고 불린다.

아르키메데스의 다면체는 카탈로니아 다면체라고 불린다.이면체 및 트라페조헤드라와 함께 이들은 정점을 가진 면 균일 고체이다.

키라리티

스너브 큐브와 스너브 12면체는 왼손잡이 형태(라틴어: Levomorph 또는 laevomorph)와 오른손잡이 형태(라틴어: dextromorph)로 나타나기 때문에 키랄로 알려져 있다.어떤 것이 서로의 3차원 거울상인 여러 형태로 나타날 때, 이러한 형태를 에난티오포맷이라고 부를 수 있다. (이 명칭은 특정 화학 화합물의 형태에도 사용된다.)

아르키메데스의 입체 구조

상세 정보:균일 다면체 및 콘웨이 다면체 표기법
아르키메데스의 고체들은 만화경에서 발생기 위치로 구성될 수 있다.

아르키메데스와 플라톤의 다른 입체들은 소수의 일반적인 구조를 사용하여 서로 연관지을 수 있다.플라토닉 솔리드에서 시작하여 모서리를 잘라냅니다.대칭을 유지하기 위해 절단은 다면체 중심에 대한 모서리를 연결하는 선에 수직인 평면에 있으며 모든 모서리에 대해 동일합니다.잘린 양(아래 표 참조)에 따라 다른 플라토닉과 아르키메데스(및 다른) 고체가 생성될 수 있습니다.인접한 정점의 각 면 쌍이 정확히 하나의 점을 공유할 수 있을 정도로 절단이 충분히 깊으면 이를 정류라고 합니다.확장 또는 칸테레이션은 각 면을 중심에서 멀리(플라톤 고체의 대칭을 보존하기 위해 같은 거리만큼) 이동하고 볼록한 선체를 취하는 것을 포함한다.비틀림을 수반하는 팽창은 면을 회전시켜 모서리에 대응하는 각 직사각형을 직사각형의 대각선 중 하나에 의해 두 개의 삼각형으로 분할하는 것도 포함한다.여기서 사용하는 마지막 구성은 모서리와 모서리 둘 다 잘라내는 것입니다.스케일링을 무시하면 팽창이 정류 상태를 확인할 수도 있습니다.마찬가지로, 칸티트랜테이션은 정류의 절단이라고 볼 수 있습니다.

아르키메데스의 입체 구조
대칭 사면체
Tetrahedral reflection domains.png 		팔면체
Octahedral reflection domains.png 		이십면체
Icosahedral reflection domains.png
솔리드 시작
작동		 기호.
{p,q}
CDel node 1.pngCDel p.pngCDel node.pngCDel q.pngCDel node.png 		사면체
{3,3}
Uniform polyhedron-33-t0.png		 큐브
{4,3}
Uniform polyhedron-43-t0.svg		 팔면체
{3,4}
Uniform polyhedron-43-t2.svg		 십이면체
{5,3}
Uniform polyhedron-53-t0.svg		 이십면체
{3,5}
Uniform polyhedron-53-t2.svg
잘라내기(t) t{p,q}
CDel node 1.pngCDel p.pngCDel node 1.pngCDel q.pngCDel node.png 		깎은 사면체
Uniform polyhedron-33-t01.png		 잘린 입방체
Uniform polyhedron-43-t01.svg		 잘린 팔면체
Uniform polyhedron-43-t12.svg		 잘린 12면체
Uniform polyhedron-53-t01.svg		 깎은 20면체
Uniform polyhedron-53-t12.svg
수정(r)
Ambo(a)		 r{p,q}
CDel node.pngCDel p.pngCDel node 1.pngCDel q.pngCDel node.png 		사면체
(8면체)
Uniform polyhedron-33-t1.png		 육팔면체
Uniform polyhedron-43-t1.svg		 이십이면체
Uniform polyhedron-53-t1.svg
비트런케이션 (2t)
듀얼키(dk)		 2t{p,q}
CDel node.pngCDel p.pngCDel node 1.pngCDel q.pngCDel node 1.png 		깎은 사면체
Uniform polyhedron-33-t12.png		 잘린 팔면체
Uniform polyhedron-43-t12.png		 잘린 입방체
Uniform polyhedron-43-t01.svg		 깎은 20면체
Uniform polyhedron-53-t12.svg		 잘린 12면체
Uniform polyhedron-53-t01.svg
양방향화(2r)
듀얼(d)		 2r{p,q}
CDel node.pngCDel p.pngCDel node.pngCDel q.pngCDel node 1.png 		사면체
Uniform polyhedron-33-t2.png		 팔면체
Uniform polyhedron-43-t2.svg		 입방체
Uniform polyhedron-43-t0.svg		 20면체
Uniform polyhedron-53-t2.svg		 12면체
Uniform polyhedron-53-t0.svg
칸테레이션(rr)
확장(e)		 rr{p,q}
CDel node 1.pngCDel p.pngCDel node.pngCDel q.pngCDel node 1.png 		마름비테트라면체
(6팔면체)
Uniform polyhedron-33-t02.png		 마름모꼴 팔면체
Uniform polyhedron-43-t02.png		 마름모꼴 십이면체
Uniform polyhedron-53-t02.png
스너브 수정 완료(sr)
스누브		 sr{p,q}
CDel node h.pngCDel p.pngCDel node h.pngCDel q.pngCDel node h.png 		스너브 사면체
(이십면체)
Uniform polyhedron-33-s012.svg		 스너브 육팔면체
Uniform polyhedron-43-s012.png		 스누브 이십이면체
Uniform polyhedron-53-s012.png
캔티트런케이션(tr)
베벨(b)		 tr{p,q}
CDel node 1.pngCDel p.pngCDel node 1.pngCDel q.pngCDel node 1.png 		절삭 사면체
(표준 8면체)
Uniform polyhedron-33-t012.png		 깎은 정육면체
Uniform polyhedron-43-t012.png		 깎은 이십이면체
Uniform polyhedron-53-t012.png

입방체와 8면체, 그리고 12면체와 20면체 사이의 이중성에 주목하십시오.또한 부분적으로는 사면체가 자기 쌍대이기 때문에, 최대 사면체 대칭을 갖는 아르키메데스의 고체는 하나밖에 없다. (사면체 대칭이 (즉, 에 포함됨) 팔면체와 동면체 대칭의 대칭 연산이기 때문에) 팔면체와 동면체 대칭이 vi일 수 있다는 사실에 의해 증명된다.정류된 사면체로서 ewed를 사용하고, 스너브 사면체로 사용할 수 있습니다.)

입체 투영

깎은 사면체 잘린 입방체 잘린 팔면체 잘린 12면체 깎은 20면체
Truncated tetrahedron stereographic projection triangle.png
삼각형의		 Truncated tetrahedron stereographic projection hexagon.png
육각형 중심의		 Truncated cube stereographic projection octagon.png
팔각형 중심의		 Truncated cube stereographic projection triangle.png
삼각형의		 Truncated octahedron stereographic projection square.png
정사각형 중심의		 Truncated octahedron stereographic projection hexagon.png
육각형 중심의		 Truncated dodecahedron stereographic projection decagon.png
데카곤 중심의		 Truncated dodecahedron stereographic projection triangle.png
삼각형 중심		 Truncated icosahedron stereographic projection pentagon.png
오각형 중심의		 Truncated icosahedron stereographic projection hexagon.png
육각형 중심의
육팔면체 이십이면체 마름모꼴 팔면체 마름모꼴 십이면체
Cuboctahedron stereographic projection square.png
정사각형 중심의		 Cuboctahedron stereographic projection triangle.png
삼각형의		 Cuboctahedron stereographic projection vertex.png
정점 중심의		 Icosidodecahedron stereographic projection pentagon.png
오각형 중심의		 Icosidodecahedron stereographic projection triangle.png
삼각형의		 Rhombicuboctahedron stereographic projection square.png
정사각형 중심의		 Rhombicuboctahedron stereographic projection square2.png
정사각형 중심의		 Rhombicuboctahedron stereographic projection triangle.png
삼각형의		 Rhombicosidodecahedron stereographic projection pentagon'.png
펜타곤 중심의		 Rhombicosidodecahedron stereographic projection triangle.png
삼각형 중심		 Rhombicosidodecahedron stereographic projection square.png
정사각형 중심
깎은 정육면체 깎은 이십이면체 스너브 큐브
Truncated cuboctahedron stereographic projection square.png
정사각형 중심의		 Truncated cuboctahedron stereographic projection hexagon.png
육각형 중심의		 Truncated cuboctahedron stereographic projection octagon.png
팔각형 중심의		 Truncated icosidodecahedron stereographic projection decagon.png Truncated icosidodecahedron stereographic projection hexagon.png Truncated icosidodecahedron stereographic projection square.png Snub cube stereographic projection.png
정사각형 중심의

「 」를 참조해 주세요.

인용문

  1. ^ Steckles, Katie. "The Unwanted Shape". YouTube. Retrieved 20 January 2022.
  2. ^ a b Grünbaum (2009년).
  3. ^ 필드 J, 아르키메데스 다면체의 재발견: 피에로 델라 프란체스카, 루카 파치오리, 레오나르도 다빈치, 알브레히트 뒤러, 다니엘레 바르바로, 요하네스 케플러, 정확과학사문서보관소, 50, 1997, 227
  4. ^ Malkevitch (1988), 85페이지

일반 참고 자료

  • .에 재인쇄되었습니다Grünbaum, Branko (2009), "An enduring error", Elemente der Mathematik, 64 (3): 89–101, doi:10.4171/EM/120, MR 2520469.
  • 를 클릭합니다Jayatilake, Udaya (March 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette. 89 (514): 76–81. doi:10.1017/S0025557200176818. S2CID 125675814..
  • 를 클릭합니다Malkevitch, Joseph (1988), "Milestones in the history of polyhedra", in Senechal, M.; Fleck, G. (eds.), Shaping Space: A Polyhedral Approach, Boston: Birkhäuser, pp. 80–92.
  • Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. 제2장
  • Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (섹션 3~9)
  • 를 클릭합니다Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (2008). "New light on the rediscovery of the Archimedean solids during the renaissance". Archive for History of Exact Sciences. 62 (4): 457–467. Bibcode:2008AHES...62..457S. doi:10.1007/s00407-008-0024-z. ISSN 0003-9519. S2CID 122216140..

외부 링크