등각형상
Isogonal figure기하학에서 폴리토프(예를 들어 폴리곤, 다면체 또는 타일링)는 모든 정점이 그림의 대칭에서 등가하면 등각 또는 정점 변환이다. 이는 각 꼭지점이 같은 종류의 얼굴로 둘러싸여 있고, 같은 순서 또는 역순으로, 같은 각도로 해당 얼굴 사이에 있다는 것을 의미한다.
기술적으로, 우리는 어떤 두 꼭지점에 대해서도 첫 번째 등축도를 두 번째에 매핑하는 폴리토프의 대칭성이 존재한다고 말한다. 이것을 말하는 다른 방법으로는 폴리토프의 자동모형 집단이 그것의 정점에 대해 전이적으로 작용하거나, 정점이 하나의 대칭 궤도 안에 놓여 있다는 것이다.
유한 n차원 이등변형의 모든 정점은 (n-1)-sphere에 존재한다.[citation needed]
이등변형이라는 용어는 다면체에서 오랫동안 사용되어 왔다. 정점 변환은 대칭군이나 그래프 이론과 같은 현대 사상으로부터 빌린 동의어다.
이등변성이 아닌 유사 옴비큐브옥타헤드론은 단순히 "모든 정점들이 같아 보인다"고 주장하는 것이 다면체나 타일링을 보존하는 이등변수 집단을 포함하는 여기서 사용되는 정의만큼 제한적이지 않다는 것을 보여준다.
등각 폴리곤과 아페이로곤
| 등각아페이로곤스 |
|---|
 |
| 등각 꼬치 아페이로곤 |
모든 일반 다각형, 아페이로곤, 일반 별 다각형은 등각형이다. 이등 다각형의 이중은 동위원소 다각형이다.
직사각형처럼 두 개의 가장자리 길이를 번갈아 하는 일부 짝수 면 폴리곤과 아페이로곤은 등각이다.
모든 평면 이등분 2n-gon은 중간 가장자리 포인트에 걸쳐 반사선이 있는 이음 대칭(Dn, n = 2, 3, ...)을 가진다.
| D2 | D3 | D4 | D7 |
|---|---|---|---|
 동일한 정점을 공유하는 등각 직사각형 및 교차 직사각형 | 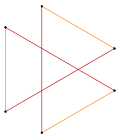 정점 6개와 에지 길이가 2개인 등각 육각형.[1] | 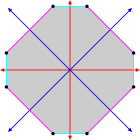 청색 및 적색 방사상 반사선이 있는 등각 볼록 8각형 | 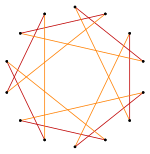 꼭지점 유형이[2] 1개이고 가장자리 유형이 2개인 등각 "별" 테트라데카곤 |
등각 다면체 및 2D 기울기
 |
| 왜곡 사각 타일링 |
 |
| A 일그러진 것 잘린 사각 타일링 |
등각 다면체와 2D 타일링은 하나의 꼭지점을 가지고 있다. 모든 정규면이 있는 등각 다면체도 균일한 다면체로서 각 정점 주위의 면들을 배열하는 정점 구성 표기법으로 나타낼 수 있다. 균일한 다면체와 틸팅의 기하학적으로 왜곡된 변화도 정점 구성을 제공할 수 있다.
| D3d, 주문 12 | Th 주문 24 | 오h 주문 48 | |
|---|---|---|---|
| 4.4.6 | 3.4.4.4 | 4.6.8 | 3.8.8 |
 왜곡된 육각 프리즘(이형 사다리꼴) |  일그러진 롬비큐옥타헤드론 | 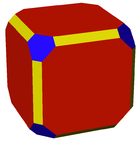 얕게 잘린 큐옥타헤드론 |  초토화 큐브 |
등각 다면체 및 2D 기울기는 다음과 같이 추가로 분류할 수 있다.
- 등면체(얼굴-변환) 및 동위원소(에지-변환)인 경우 일반적이다. 이는 모든 얼굴이 동일한 종류의 일반 폴리곤임을 의미한다.
- 동위원소(에지-변환)이지만 등면(얼굴-변환)이 아닌 경우 준규칙.
- 모든 면이 일반 폴리곤이지만 등면(얼굴-변환) 또는 동위원소(에지-변환)가 아닌 경우 반정형. (정의는 저자에 따라 달라진다. 예를 들어, 일부 고형분들은 이음 대칭이 있는 고형분 또는 비 컨벡스 고형분들을 제외한다.)
- 모든 얼굴이 규칙적인 다각형인 경우 균일함, 즉 규칙적인, quasiregular 또는 반규칙적인 경우.
- 그 원소도 등각인 경우 반 균일함.
- 모든 가장자리의 길이가 같은 경우 scaliform.
- 등면체(얼굴-변환)인 경우 고결하다.
N 치수: 등각 폴리탑 및 테셀레이션
이러한 정의는 고차원적인 폴리토페와 테셀레이션으로 확장될 수 있다. 예를 들어, 모든 균일한 폴리토프는 균일한 4폴리토프와 볼록한 균일한 벌집형이다.
이등각 폴리토프의 이중은 등면체형이며, 그 면에 전이형이다.
k-이항 및 k-수치
폴리토프 또는 타일링은 그것의 정점이 k transitivity 클래스를 형성하는 경우 k-이등성이라고 불릴 수 있다. 보다 제한적인 용어인 k-uniform은 정규 다각형에서만 구성된 k-이등변형으로 정의된다. 그것들은 다른 균일한 색상으로 시각적으로 색상으로 표현될 수 있다.
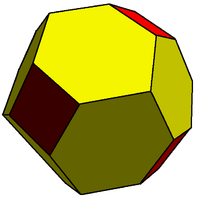 잘린 이 심방 도데카헤드론은 정점의 두 개의 전이성 클래스를 포함하고 있기 때문에 2-이항성이다. 이 다면체는 정사각형과 납작한 육각체로 만들어졌다. |  이 단층 타일링도 2등분(및 2등분)이다. 이 타일링은 정삼각형과 정육각형의 면으로 만들어졌다. |  2-이항 9/4 에네그램(이코사헤드론 최종면) |
참고 항목
참조
- 피터 R. Cromwell, Polyedra, Cambridge University Press 1997, ISBN0-521-55432-2, 페이지 369 Transitivity
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. (p. 33 k-등각 타일링, 페이지 65 k-높이 기울기)
외부 링크
- Weisstein, Eric W. "Vertex-transitive graph". MathWorld.
- Olshevsky, George. "Transitivity". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Olshevsky, George. "Isogonal". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- 2000년 8월 21–24일, 시애틀, WA VRML 모델, 오레곤 주립대학 물리학부, 코발리스, Mosaic2000, 밀레니얼 오픈 심포지엄 예술 및 학제간 컴퓨팅에서 발표
- Steven Dutch는 k-uniform이라는 용어를 k-이등각 기울기를 열거하는 데 사용한다.
- n-균일 기울기 목록
- Weisstein, Eric W. "Demiregular tessellations". MathWorld. (k-등각의 경우 k-uniform이라는 용어를 사용함)

